I 型和 II 型錯誤：優化中不可避免的錯誤

當您在實驗中錯誤地發現獲勝者或未能發現它們時，就會發生 I 型和 II 型錯誤。 有了這兩個錯誤，您最終會選擇似乎可行或不可行的方法。 而不是真正的結果。

對測試結果的誤解不僅會導致錯誤的優化工作，而且從長遠來看還會使您的優化計劃脫軌。

捕捉這些錯誤的最佳時機是在你犯錯之前！ 因此，讓我們看看如何在優化實驗中避免遇到 I 型和 II 型錯誤。

但在此之前，讓我們看一下原假設……因為是錯誤拒絕或不拒絕原假設導致 I 型和 II 型錯誤。

零假設：​H0

當您假設一個實驗時，您不會直接跳到建議提議的更改將移動某個指標。

您首先說提議的更改根本不會影響相關的指標——它們是不相關的。

這是您的零假設 (H0)。 H0 始終表示沒有變化。 默認情況下，這就是您所相信的……直到（並且如果）您的實驗證明了它。

您的替代假設（Ha 或 H1）是存在積極變化。 H0 和 Ha 在數學上總是對立的。 Ha 是您期望提議的更改產生影響的那個，它是您的替代假設 - 這就是您正在通過實驗測試的內容。

因此，例如，如果您想在定價頁面上運行一個實驗並向其中添加另一種付款方式，您首先會形成一個零假設，即：額外的付款方式不會對銷售產生影響。 你的替代假設是：額外的付款方式將增加銷售額。

事實上，進行實驗是在挑戰零假設或現狀。

當您錯誤地拒絕或未能拒絕原假設時，就會發生 I 型和 II 型錯誤。

了解 I 類錯誤

I 類錯誤稱為誤報或 Alpha 錯誤。

在假設檢驗的 I 類錯誤實例中，您的優化測試或實驗 *似乎是成功的 *並且您（錯誤地）得出結論，您正在測試的變體與原始版本不同（更好或更差）。

在第一類錯誤中，你會看到上升或下降——這只是暫時的，不太可能長期維持——最終會拒絕你的原假設（並接受你的替代假設）。

錯誤地拒絕零假設可能有多種原因，但最主要的原因是偷看（即，在中間或實驗仍在運行時查看您的結果）。 並在達到設定的停止標準之前調用測試。

許多測試方法不鼓勵偷看的做法，因為查看中間結果可能會導致錯誤的結論，從而導致 I 類錯誤。

以下是你如何犯 I 類錯誤：

假設您正在優化 B2B 網站的登錄頁面，並假設向其添加徽章或獎勵會減少潛在客戶的焦慮，從而提高表單填寫率（導致更多潛在客戶）。

因此，您對該實驗的零假設變為：添加徽章對錶單填寫沒有影響。

這種實驗的停止標准通常是某個時期和/或在 X 轉換發生在設定的統計顯著性水平之後。 傳統上，優化器會嘗試達到 95% 的統計置信度標記，因為它使您有 5% 的機會出現對於大多數優化實驗而言被認為足夠低的 I 類錯誤。 一般來說，這個指標越高，犯第一類錯誤的機會就越低。

您所追求的置信水平決定了您出現 I 類錯誤 (α) 的概率。

因此，如果您的目標是 95% 的置信水平，您的 α 值將變為 5%。 在這裡，你承認你的結論有 5% 的可能性是錯誤的。

相比之下，如果您的實驗置信度為 99%，那麼您出現 I 類錯誤的概率會下降到 1%。

假設，對於這個實驗，您太不耐煩了，而不是等待實驗結束，您只需一天就查看測試工具的儀表板（偷看！）。 您會注意到“明顯”的提升——您的表單填寫率以 95% 的置信水平上升了 29.2%。

和巴姆…

……你停止你的實驗。

…拒絕零假設（徽章對銷售沒有影響）。

…接受替代假設（徽章促進銷售）。

......並運行帶有獎項徽章的版本。

但是，當您衡量一個月內的潛在客戶時，您會發現該數字幾乎與您使用原始版本報告的數字相當。 畢竟，徽章並不重要。 並且零假設可能被徒勞地拒絕了。

這裡發生的情況是，你過早地結束了實驗，拒絕了原假設，最終得到了一個錯誤的贏家——犯了 I 類錯誤。

避免實驗中的 I 類錯誤

降低您遇到 I 類錯誤的機會的一種可靠方法是提高置信水平。 5% 的統計顯著性水平（轉化為 95% 的統計置信水平）是可以接受的。 這是一個大多數優化器都會安全地做出的賭注，因為在這裡，你會在不太可能的 5% 範圍內失敗。

除了設置高置信度之外，運行足夠長時間的測試也很重要。 測試持續時間計算器可以告訴您必須運行測試多長時間（在考慮到指定的效果大小等因素之後）。 如果您讓實驗按預期進行，您會顯著降低遇到類型 1 錯誤的機會（假設您使用的是高置信度）。 等到您獲得具有統計意義的結果可確保您錯誤地拒絕原假設並犯下 I 類錯誤的可能性很小（通常為 5%）。 換句話說，使用良好的樣本量，因為這對於獲得具有統計意義的結果至關重要。

現在這都是關於與實驗中的置信度（或顯著性）相關的 I 型錯誤。 但是還有另一種類型的錯誤也會潛入你的測試——II 型錯誤。

了解 II 類錯誤

II 類錯誤稱為假陰性或 Beta 錯誤。

與 I 類錯誤相比，在 II 類錯誤的情況下，實驗*似乎不成功（或不確定）*並且您（錯誤地）得出結論，您正在測試的變體與原來的。

在 II 型錯誤中，您看不到真正的上升或下降，最終無法拒絕原假設並拒絕備擇假設。

以下是你如何犯第二類錯誤：

從上面回到同一個 B2B 網站……

因此，假設這次您假設在表單頂部顯著添加 GDPR 合規免責聲明將鼓勵更多潛在客戶填寫（導致更多潛在客戶）。

因此，您對此實驗的零假設變為： GDPR 合規性免責聲明不會影響表單填寫。

相同的替代假設是： GDPR 合規性免責聲明導致更多的表格填寫。

如果存在任何偏差，測試的統計能力決定了它可以檢測到原始版本和挑戰者版本的性能差異的能力。 傳統上，優化器試圖達到 80% 的統計功效標記，因為該指標越高，出現 II 型錯誤的機會就越低。

統計功效取一個介於 0 和 1 之間的值（通常以 % 表示）並控制您的 II 型錯誤 (β) 的概率； 它的計算公式為：1 – β

測試的統計功效越高，遇到 II 類錯誤的概率就越低。

因此，如果一個實驗的統計功效為 10%，那麼它很容易受到 II 型錯誤的影響。 然而，如果一個實驗的統計功效為 80%，那麼它犯 II 類錯誤的可能性就會小得多。

同樣，您運行測試，但這次您沒有註意到表單填寫有任何顯著提升。 兩個版本都報告了接近相似的轉化率。 因此，您將停止實驗並繼續使用原始版本，而無需遵守 GDPR 合規性免責聲明。

然而，當您深入研究實驗期間的潛在客戶數據時，您會發現雖然兩個版本（原始版本和挑戰者）的潛在客戶數量似乎相同，但 GDPR 版本確實讓您的數量有了很好的顯著上升來自歐洲的線索。 （當然，您可以使用受眾定位來僅向來自歐洲的潛在客戶展示該實驗——但這是另一回事。）

這裡發生的情況是你過早地結束了測試，沒有檢查你是否獲得了足夠的力量——犯了第二類錯誤。

避免實驗中的 II 型錯誤

為避免 II 類錯誤，請運行具有高統計功效的測試。 嘗試配置您的實驗，以便您可以達到至少 80% 的統計功效標記。 對於大多數優化實驗來說，這是一個可接受的統計功效水平。 有了它，您可以確保至少在 80% 的情況下，您將正確拒絕錯誤的零假設。

為此，您需要查看增加它的因素。

其中最大的是樣本量（給定觀察到的效應量）。 樣本量直接關係到檢驗的功效。 巨大的樣本量意味著高功效測試。 動力不足的測試非常容易受到 II 類錯誤的影響，因為您檢測到挑戰者和原始版本結果差異的機會大大降低，尤其是對於低 MEI（更多信息見下文）。 因此，為避免 II 類錯誤，請等待測試積累足夠的功率以最大限度地減少 II 類錯誤。 理想情況下，對於大多數情況，您希望達到至少 80% 的功率。

另一個因素是您為實驗設定的最小感興趣效應 (MEI) 。 MEI（也稱為 MDE）是您希望在相關 KPI 中檢測到的最小差異幅度。 如果您設置較低的 MEI（例如，關注 1.5% 的提升），則遇到 II 型錯誤的機會會增加，因為檢測小的差異需要更大的樣本量（以獲得足夠的功效）。

最後，重要的是要注意，犯 I 類錯誤的概率 (α) 和犯 II 類錯誤的概率 (β) 之間往往存在反比關係。 例如，如果您降低 α 的值以降低犯 I 類錯誤的概率（假設您將 α 設置為 1%，意味著置信水平為 99%），則您的實驗的統計功效（或其能力，β ，當存在差異時檢測到差異）最終也會減少，從而增加您出現 II 型錯誤的可能性。

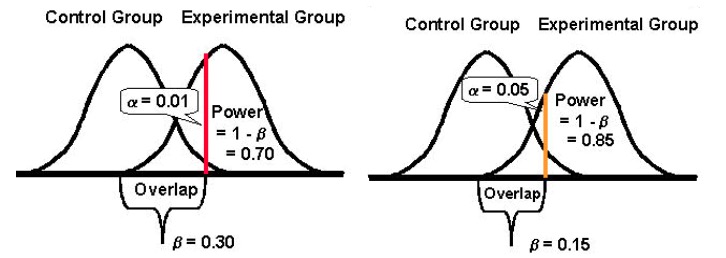
更容易接受任何一種錯誤：I型和II型（並取得平衡）

降低一種錯誤的概率會增加另一種錯誤的概率（假設所有其他內容保持不變）。

因此，您需要決定您可以更容忍的錯誤類型。

一方面，犯 I 類錯誤並為所有用戶推出更改可能會花費您的轉化和收入——更糟糕的是，也可能成為轉化殺手。

另一方面，如果犯了 II 類錯誤，並且未能為所有用戶推出成功的版本，可能會再次使您失去原本可以贏得的轉化。

總是，這兩個錯誤都是有代價的。

但是，根據您的實驗，您可能會比另一種更容易接受。 一般來說，測試人員發現第一類錯誤比第二類錯誤嚴重四倍。

如果您想採取更平衡的方法，統計學家 Jacob Cohen 建議您應該選擇 80% 的統計功效，同時“在 alpha 和 beta 風險之間取得合理的平衡”。 ”（80% 的功率也是大多數測試工具的標準。）

而就統計顯著性而言，標准設定為95%。

基本上，這都是關於妥協和你願意容忍的風險水平。 如果您想真正最小化這兩種錯誤的可能性，您可以選擇 99% 的置信度和 99% 的功效。 但這意味著您將在看似永恆漫長的時期內使用不可能巨大的樣本量。 此外，即使那樣你也會留下一些錯誤的餘地。

每隔一段時間，你就會錯誤地結束一個實驗。 但這是測試過程的一部分——掌握 A/B 測試統計數據需要一段時間。 調查和重新測試或跟進您成功或失敗的實驗是重申您的發現或發現您犯了錯誤的一種方法。