用你的編程意識感受微積分

我相信會編程的人——有能力理解比微積分更複雜的概念。 有許多才華橫溢的程序員仍在為微積分苦苦掙扎的一個原因並不是它很難。 這主要是因為我們以錯誤的方式教授它（以及許多其他主題）。

如果你在生活中做過一些編碼——甚至是一些玩具練習，比如生成素數，你可能已經做過類似的事情，這些事情發生在微積分中，但從來沒有機會聯繫起來。

寫這篇文章的目的既不是教你微積分也不是編程——而是幫助你連接一些點。

我將在一分鐘後進入編碼部分。 但請允許我在此之前簡要介紹一下背景。

變化率

微積分談論“變化率”。 讓我們試著理解這意味著什麼。

對於變量 (x) 的變化，函數的變化率就是函數的變化除以 x 的變化。 讓我們用實際數字可視化：

考慮 2 個點 x=2 和 x=6，以及函數 y=f(x) = x²。

另外，考慮dx = x 軸上這兩個點之間的距離。 dy是這些 x 值的 y 值之間的距離。

那麼，y 從 x=2 到 x=6 的變化率是

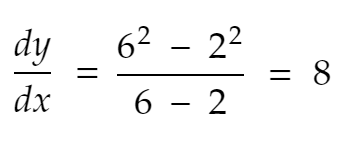
衍生物

現在——導數 dy/dx 是 x 的無限小的變化時 y 的變化率。 由於這個距離 (6–2=4) 不是無限小——甚至不是很近，我們不能將上述方程稱為導數。 所以，現在讓我們選擇一個較小的數字， 0.1 。

當 x = 0 時，y = x² = 0² = 0。

正方向的最近鄰，x = 0.1。 y 變為 0.1² = 0.01。

所以，

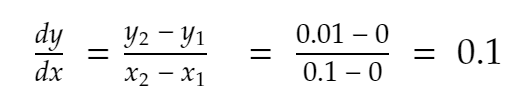
讓我們再試一次。 0.1 到正方向的最近鄰，x = 0.2。 因此，y 變為 0.2² = 0.04。 所以，

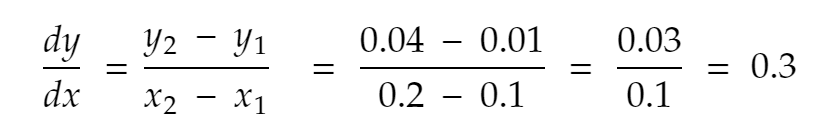
如果我們再重複這個過程幾次，這就是我們得到的：

如果你想玩它，這裡是 excel 文件。

在我們的上下文中， dx （這是我們虛構的 x 軸上 2 個相鄰點之間的無限小距離）是 0.1。

x相應增加。

y就是 x²。

dy是 2 個相鄰 y 值之間的距離。 例如，當 x= 0.1 時，當前 y (0.01 ) 和下一個 y (0.04) 之間的距離為 0.03 — 因此，在 x=0.1 時 dy 為 0.03。

dy/dx是 dy 除以 dx。

dy/dx / x是 dy/dx 除以 x。

現在請注意，隨著 x 的增加，最後一行接近 2，這意味著 — x² 相對於 x 的變化率接近 x 的兩倍，即2x 。

還記得 x² 關於 x 的導數嗎？ 2倍！ 找到一些聯繫？

編碼時間

讓我們嘗試一下我們迄今為止討論過的代碼。

假設您已經安裝了 Python，在終端中運行：

之後，運行以下 Python 代碼：

這裡：

x ：包含從 0 到 9 的數字。

y : 另一個數組，每個元素都是對應 x 元素的平方

dy ：另一個用零初始化的數組。 我們將把 y 距離放在這個數組中。

dydx ：另一個用零初始化的數組。 它將包含每個點的 dy/dx 值。

dx ：很明顯——它是步長。 2 個連續數字之間的距離，隨著 SIZE 的增加而減小。 如果 SIZE = 10，dx = 1。如果 SIZE = 100，dx = 0.1。

首先，我們為每個點推導 dy。 然後我們從中計算 dydx。

請注意：

在這裡，我們省略了第一個和最後一個值。 x 的第一個值為 0，這將產生零除錯誤。 而且我們無法計算 dy/dx 的最後一個值，因為我們沒有 dy 的最後一個值——因為它需要 y 的最後一個可用值，而我們這裡沒有。

如果一切順利，你會得到這個圖表：

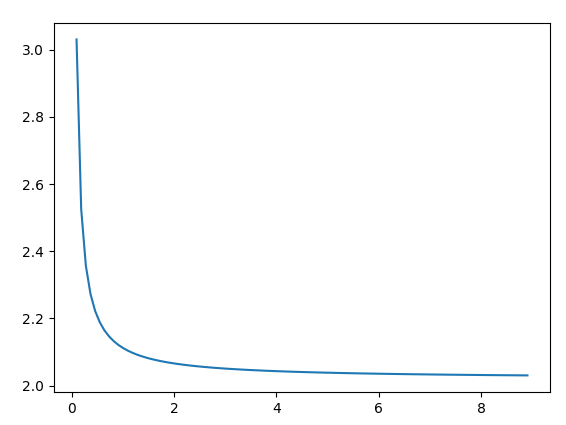
你從劇情中了解到的

如您所見，圖表正在接近 2。增加 SIZE 的值（意味著將 dx 設置得更低）並查看圖表如何更快地接近 2。

二階導數

既然您已經走到了這一步，只需再執行幾個步驟即可實現二階導數，這將使您對任意階的導數有了直覺。

如您所知，二階導數是一階導數相對於 x 的變化率。 簡單地說——二階導數中的 dy/dx 就像一階導數中的 y。

讓我們對上面的代碼做如下修改：

再聲明 2 個數組：

d2ydx2 ：這將代表二階導數：

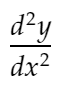
distance_dydx：表示 2 個相鄰點之間 dy/dx 值之間的距離

這是二階導數的完整代碼：

在 for 循環中計算 dydx 後，我們執行另一個循環來計算二階導數。 通過一些明智的編碼，我們可以在同一個循環中計算二階導數（嘗試作為練習）——但為了清楚起見，我在這裡將它們分開。

另外，請注意：

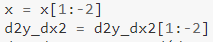
正如我們在一階導數中所做的那樣，我們也在這裡省略了一些值。 最後兩個值被省略，因為倒數第二個需要最後一個“一階導數”值，我們無法計算（因為我們沒有所需的 y 值——如上所述）。 這是否意味著在三階導數的情況下我們必須省略最後 3 個值？🤔 - 那是你自己找的。

這是輸出圖：

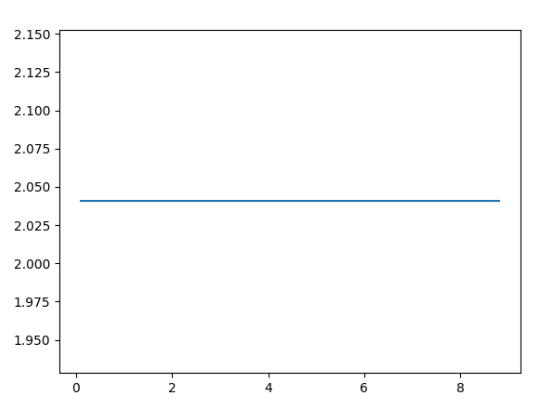
我們在這裡看到了什麼？

高中時就知道：

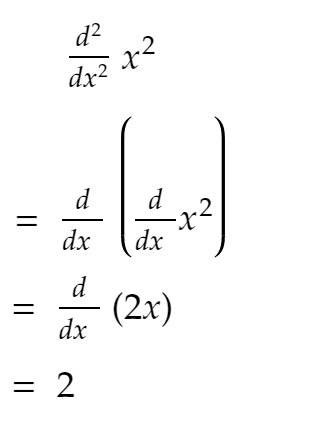
現在，正如您從上面的代碼中看到的那樣，二階導數大部分保持不變，如果您繼續增加 SIZE — 它接近 2！

為什麼變化率很重要

你可能想知道：

——我們為什麼要經歷所有這些討厭的麻煩？ 我們從變化率或導數中得到什麼有用的信息？

— 為什麼我們不能隨隨便便的變化率而變化？ 為什麼只有無限小？ 我們從關於無窮小的變化率中得到什麼信息，而這些信息不能從關於較大值的變化率中找到？

——這個無限小的東西有點像黑客？ 我們處理了一些上面的小數字，但實際上肯定不是無限小。

如果我允許自己繼續下去，你會看到這篇文章的長度走開，不會走到這一步。 也許改天我們會解決這些問題😀。