貝葉斯統計:A/B 測試人員的快速且無炒作的入門讀物
已發表: 2022-06-23
您對解釋 A/B 測試工具提供的結果的能力有多大信心?
假設您使用的是基於貝葉斯統計的工具,它告訴您“B”有 70% 的機會擊敗“A”,因此“B”是贏家。 您知道這意味著什麼以及它應該如何影響您的 CRO 策略嗎?
在本文中,您將學習貝葉斯統計的基礎知識,這將幫助您重新控制 A/B 測試,包括
- 貝葉斯統計的公正觀點
- 頻率論與貝葉斯的優缺點
- 您需要自信地解釋和使用貝葉斯 A/B 測試結果,同時避免一些常見的神話陷阱。
- 什麼是貝葉斯統計?
- 貝葉斯起源故事
- 應用於 A/B 測試的貝葉斯統計示例
- 對 A/B 測試人員很重要的貝葉斯術語簡短詞彙表
- 貝葉斯推理
- 條件概率
- 概率分佈/似然分佈
- 先驗信念分佈
- 共軛
- 共軛先驗
- 損失函數
- 什麼是頻率統計?
- 貝葉斯與頻率論 A/B 測試
- 頻率論者框架
- 貝葉斯框架
- 貝葉斯統計實際上在 A/B 測試中告訴您什麼?
- 成為最好的概率 (P2BB)
- 預期提升
- 預期損失
- 要避免的有關貝葉斯統計的神話
- 誤區一:貝葉斯主義者陳述他們的假設,頻率論者沒有
- 神話#2。 貝葉斯方法給你你真正想要的答案
- 誤區 3:貝葉斯推理比頻率推理更能幫助您傳達不確定性
- 神話#4。 貝葉斯 A/B 測試結果不受偷窺
- 神話#5。 頻率統計是低效的,因為您必須等待固定的樣本量
- 那麼,您應該選擇貝葉斯還是頻率主義者? 兩者都有一個地方。
- 關鍵要點
準備好? 讓我們從基礎開始。
什麼是貝葉斯統計?
貝葉斯統計是一種基於貝葉斯定理的統計分析方法,它在收集有關這些事件的新數據或證據時更新對事件的信念。 在這裡,概率是對事件發生的信念的度量。
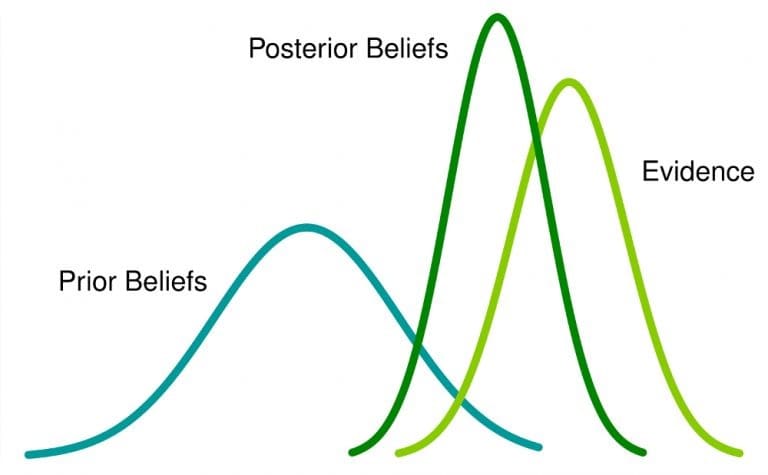
這意味著什麼:如果您對某個事件有先驗信念,並獲得更多相關信息,那麼該信念將改變(或至少被調整)為後驗信念。
這對於理解不確定性或處理大量嘈雜數據很有用,例如電子商務的轉化率優化和機器學習。
讓我們想像一下:
舉例來說,你正在觀看一場大學購物車比賽,然後一位興奮的觀眾向你發起挑戰,打賭那個穿紅色 T 恤的傢伙推著穿綠色襯衫的女士會贏。 您考慮一下並反駁說,黑色夾克男和黑色連帽衫女孩會取而代之。

頭頂上的另一位觀眾低聲向你小聲提示:“紅色 T 卹男贏得了 4 場比賽中的最後 3 場比賽。” 你的賭注會怎樣? 你已經不太確定了,對吧?
假設您還了解到,上次黑夾克男戴上他的幸運太陽鏡時,他贏了。 而他不穿的時候,那個紅T恤的人贏了。
今天,你看到那個黑夾克的傢伙戴著那副眼鏡。 你的信念再次改變。 你現在對自己的賭注更有信心了,對嗎? 在這個故事中,每次獲得新數據的證據時,您都會更新您的信念。 這就是貝葉斯方法。
貝葉斯起源故事
當托馬斯·貝葉斯牧師第一次想到他的理論時,他認為它不值得發表。 因此,它在他的筆記中保留了十多年。 正是當他的家人要求理查德·普萊斯檢查他的筆記時,普萊斯發現了構成貝葉斯定理基礎的筆記。
它始於貝葉斯的思想實驗。 他想著背對著一張完全平坦的方形桌子,讓助手把球扔到桌子上。
球可以落在桌子上的任何地方,但貝葉斯認為他可以通過用新信息更新他的猜測來猜測哪裡。 當球落在桌子上時,他會讓助手告訴他它是落在左邊還是右邊,前一個球落在了前面還是後面。
他注意到了這一點,並聽著更多的球落在桌子上。 有了這樣的額外信息,他發現他可以提高每次投擲的猜測準確性。 隨著我們從觀察中獲得更多證據,這帶來了更新我們理解的想法。
貝葉斯數據分析方法應用於科學和工程等各個領域,甚至包括體育和法律。
在在線隨機對照實驗中,特別是 A/B 測試中,您可以通過 4 個步驟使用貝葉斯方法:
- 確定您的先前分佈。
- 選擇一個反映您的信念的統計模型。
- 運行實驗。
- 觀察後,更新你的信念併計算後驗分佈。
您使用一組稱為貝葉斯算法的規則來更新您的信念。
應用於 A/B 測試的貝葉斯統計示例
讓我們舉例說明一個貝葉斯 A/B 測試示例。
想像一下,我們在 Shopify 商店的 CTA 按鈕上運行了一個簡單的 A/B 測試。 對於“A”,我們使用“添加到購物車”,對於“B”,我們使用“添加到您的購物車”。
以下是常客將如何進行測試。
有兩個可供選擇的世界:一個是 A 和 B 沒有區別,因此測試不會顯示轉換率有任何差異。 這就是零假設。 而在另一個世界中,存在差異,因此一個按鈕會比另一個按鈕執行得更好。
常客會假設我們生活在世界 1,CTA 按鈕沒有區別,也就是說,假設原假設為真。 然後他們會嘗試以預先確定的確定性水平(稱為顯著性水平)證明錯誤。
但這就是貝葉斯將如何處理相同的測試:
他們首先相信按鈕 A 和 B 都有相同的機會產生 0 到 100% 之間的轉化率。 所以,一開始就有按鈕平等——兩者都有 50% 的機會成為表現最好的人。
然後開始測試並收集數據。 通過觀察新信息,貝葉斯 A/B 測試人員將更新他們的知識。 因此,如果 B 表現出希望,他們可以根據該觀察得出一個後驗信念,即“B 有 61% 的機會擊敗 A”。
這兩種方法之間存在核心差異。
這就是為什麼我們對貝葉斯 A/B 測試保持公正的方法很重要。
大多數貝葉斯 A/B 測試工具——也許是出於營銷目的——採取極端的反頻率主義立場,並推動貝葉斯更善於告訴你哪個變體更“有利可圖”的論點。
但是,是否有任何單一的 A/B 測試統計方法擁有洞察的專有權?
如果進一步推動貝葉斯論點,他們可能會面臨研究,其中受訪者說他們想知道什麼是最佳行動方案,或者他們想最大化利潤或類似的東西。 這將問題牢牢地置於決策理論領域——貝葉斯推理和頻率論推理都無法直接說明這一點。
Georgi Georgiev, Analytics-toolkit.com 的創建者和“在線 A/B 測試中的統計方法”的作者
我們將在前面的部分中簡要介紹這些細節。 現在,讓我們讓這本入門書的其餘部分易於掌握。
對 A/B 測試人員很重要的貝葉斯術語簡短詞彙表
貝葉斯推理
貝葉斯推理是用新數據更新假設的概率。 它建立在信念和概率之上。
貝葉斯推理利用條件概率來幫助我們理解數據如何影響我們的信念。 假設我們從一個先驗的信念開始,即天空是紅色的。 在查看了一些數據之後,我們很快就會意識到這種先前的信念是錯誤的。 因此,我們執行貝葉斯更新來改進我們關於天空顏色的錯誤模型,最終得到更準確的後驗信念。
邁向數據科學的邁克爾·伯克
條件概率
條件概率是給定另一個事件發生的事件的概率。 也就是條件B下A的概率。
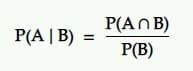
翻譯:在給定另一個事件 B 的情況下,事件 A 發生的概率等於 B 和 A 同時發生的概率除以事件 B 的概率。
概率分佈/似然分佈
似然分佈是顯示您的數據假設特定值的可能性的分佈。
如果您的數據可以採用多個值,例如顏色類別可能是灰色、紅色、橙色、藍色等,那麼您的分佈是多項式的。 對於一組數字,分佈可能是正態的。 對於可能是/否或真/假的數據值,它將是二項式的。
先驗信念分佈
或者先驗概率分佈,簡稱為先驗,在您獲得新數據的證據之前表達了您的信念。 因此,它是您最初信念的表達,在考慮使用貝葉斯分析(或推理)的一些證據後,您將對其進行更新。
共軛
首先,共軛是指連接在一起,通常是成對的。 在貝葉斯概率論中,共軛假設先驗與可能性共軛。
如果後驗與先驗具有相同的函數形式,則先驗與似然函數共軛。 這顯示了似然函數如何更新先驗分佈。
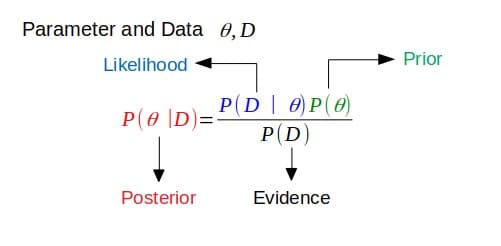
共軛先驗
這與上面的定義有關。 如果後驗與先驗概率分佈屬於同一概率分佈族(或具有相同的函數形式),則先驗和後驗是共軛分佈。 在這種情況下,先驗稱為似然函數的共軛先驗。
它們可以是主觀的(基於實驗者的知識)、客觀的和信息性的(基於歷史數據)或非信息性的。
損失函數
損失函數是一種通過測量我們當前估計的糟糕程度來量化損失的方法。 它有助於我們最大限度地減少假設檢驗的損失,特別是在表達位於一系列可能值範圍內的推論時,並用我們的測試結果支持決策。
現在一切都結束了,我們可以繼續前進。
如果您已經在這個街區呆了一段時間,那麼您可能遇到過不止一些頻率論者與貝葉斯統計模因。

雙方似乎都在從相反的方向尋找答案,但事實真的如此嗎? 為了更好地理解這一點(同時保持公正),讓我們訪問Frequentists 陣營。
什麼是頻率統計?
這是大多數人在統計學中學習的第一個推理技術。 頻率統計計算事件(假設)在相同條件下頻繁發生的概率。
使用頻率論方法的 A/B 假設檢驗遵循以下步驟:
- 宣布一些假設。 通常,零假設是新的變體“B”並不比原來的“A”好,而備擇假設則相反。
- 除非您使用順序測試方法,否則請使用統計功效計算提前確定樣本量。 使用考慮統計功效、當前轉換率和最小可檢測效果的樣本量計算器。
- 運行測試並等待每個變體暴露於預先確定的樣本量。
- 計算觀察結果的概率至少與原假設下的數據一樣極端(p 值)。 如果 p 值 < 5%,則拒絕原假設並將新變體部署到生產環境中。
這與貝葉斯相比如何? 讓我們來看看…
貝葉斯與頻率論 A/B 測試
在任何使用統計推斷的地方,這都是一場臭名昭著的辯論。 坦率地說,這是沒有意義的。 兩者都有其優點和實例,它們是最好的使用方法。
與兩個陣營中的大多數推動者所想的相反,它們在幾個方面相似,並且沒有一個比另一個更接近真相——儘管他們的方法不同。
例如,當應用於 A/B 測試時,沒有任何具體的方法可以為您提供關於將導致業務增長的行動過程的絕對準確的預測。 相反,A/B 測試可以幫助您消除決策中的風險。
無論您如何分析數據——使用貝葉斯或頻率論方法——你都可以在一定程度上確定你是對的。
因此,這兩種統計模型都是有效的。 Bayesian 可能具有速度優勢,但比Frequentist 的計算要求更高。
查看其他差異...
頻率論者框架
我們大多數人都熟悉介紹性統計課程中的常客方法。 我們定義了上述方法——從宣布零假設、確定樣本量、通過隨機實驗收集數據,最後觀察到具有統計學意義的結果。
在頻率論中,我們認為概率從根本上與重複事件的頻率相關。 因此,在公平的拋硬幣中,頻率論者認為,如果他們猜得足夠頻繁,他們將在 50% 的時間中正確地猜出正面,反面也是如此。
頻率論者的心態: “如果我在相同的條件下一遍又一遍地重複實驗,我的方法得到正確答案的機會有多大?”
貝葉斯框架
雖然常客方法將每個變量的總體參數視為(未知)常數,但貝葉斯方法將每個參數值建模為具有某種概率分佈的隨機變量。
在這裡,您可以直接計算感興趣參數的概率分佈(以及期望值)。
為了對每個變體的概率分佈進行建模,我們依靠貝葉斯規則將實驗結果與我們對感興趣度量的任何先驗知識相結合。 我們可以通過使用共軛先驗來簡化計算。
Alex Birkett 這樣總結貝葉斯算法:

- 定義包含您對參數的主觀信念的先驗分佈。 先驗可以是不提供信息的或提供信息的。
- 收集資料。
- 使用貝葉斯定理用數據更新您的先驗分佈(儘管您可以在不明確使用貝葉斯規則的情況下使用貝葉斯方法 - 請參閱非參數貝葉斯)以獲得後驗分佈。 後驗分佈是一種概率分佈,表示您在查看數據後對參數的更新信念。
- 分析後驗分佈並總結它(平均值、中位數、標準差、分位數……)。
簡而言之,貝葉斯實驗者專注於他們自己的觀點以及概率對他們意味著什麼。 他們的意見隨著觀察到的數據而發展。 另一方面,頻率論者相信正確的答案就在某個地方。
了解頻率論者與貝葉斯論者的爭論不會對 A/B 測試後的分析產生太大影響。 兩個陣營之間的主要區別更多地與可以測試的內容有關。
概率統計在後續分析中一般不會大量使用。 Bayesian-Frequentist 論點更適用於 A/B 範式中要測試的變量的選擇,但即便如此,大多數 A/B 測試人員也違反了研究假設、概率和置信區間。
Rob Balon 博士到 CXL
Georgi 進一步闡述:
有多個在線貝葉斯計算器和至少一個主要的 A/B 測試軟件供應商應用貝葉斯統計引擎,它們都使用所謂的非信息先驗(有點用詞不當,但我們不要深入研究)。 在大多數情況下,這些工具的結果在數值上與對相同數據的常客測試的結果一致。 假設貝葉斯工具將報告類似“B 優於 A 的概率為 96%”,而常客工具將產生 0.04 的 p 值,對應於 96% 的置信水平。
在上述情況下,這比某些人願意承認的要普遍得多,即使解釋不同,兩種方法都會導致相同的推論,並且不確定性水平相同。
貝葉斯對這個結果會怎麼說? 在查看沒有先驗信息的場景時,它是否會將 p 值轉換為適當的後驗概率? 還是所有這些貝葉斯測試的應用都被誤導為使用非信息性先驗本身?
真的沒有必要選擇一個營地並在掩體後面找一個地方向另一個營地扔石頭。 甚至有證據表明這兩個框架產生了相同的結果。 不管你選擇哪條路,目的地可能都是一樣的。 這取決於您如何使用Frequentist vs Bayesian到達那裡。
例如:
- 有數據表明貝葉斯測試更快,是交互式實驗的首選:
由於貝葉斯範式允許實驗者正式量化信念並結合額外的知識,它比傳統的統計分析更快。
在貝葉斯 A/B 測試模擬中,當調整決策標準(即增加對錯誤的容忍度)時,75% 的實驗在傳統方法所需觀察結果的 22.7% 範圍內結束(在 5% 的顯著性水平上)。 它只記錄了 10% 的 II 類錯誤。 - 貝葉斯也被認為更寬容,而頻率主義者則規避風險:
雖然許多頻率學檢驗使用 95% 的統計顯著性,但貝葉斯主義者可以滿足於低於此值。 如果一個變體有 78% 的機會擊敗控件,這取決於預期的損失,那麼部署該變體可能是一個合理的決定。
如果你錯了,預期損失不到百分之一,這對許多企業來說都是微不足道的損失。 這種雜亂無章的方法可能更適合在風險非常低的情況下快速做出決策。 - 然而,貝葉斯模擬和計算的計算量很大:
另一方面,頻率論者是基於筆和紙的。 警告:如果您的 A/B 測試工具使用貝葉斯,並且您不知道哪些假設被添加到您的數據中,那麼您不能依賴供應商給您的“答案”。 用少許鹽服用。 並運行您自己的分析。
貝葉斯並不全是陽光和彩虹。 就像 Georgi 用這個問題列表指出的那樣:
- “你想得到先驗概率和似然函數的乘積嗎?”
- “你想要先驗概率和數據的混合作為輸出嗎?”
- “您是否希望將主觀信念與數據混合以產生輸出?” (如果使用信息先驗)
- “您是否願意提供統計數據,其中假設與實際數據高度確定的先驗信息混合在一起?”
通俗地說,這些都是貝葉斯統計的各個方面。
貝葉斯統計實際上在 A/B 測試中告訴您什麼?
您設計了 A/B 測試以深入了解更改如何影響您感興趣的指標,例如轉化率或每位訪問者的收入。
當您使用適用於貝葉斯統計的工具時,了解結果的含義很重要,因為“B 是贏家”並不完全是大多數人認為的那樣。
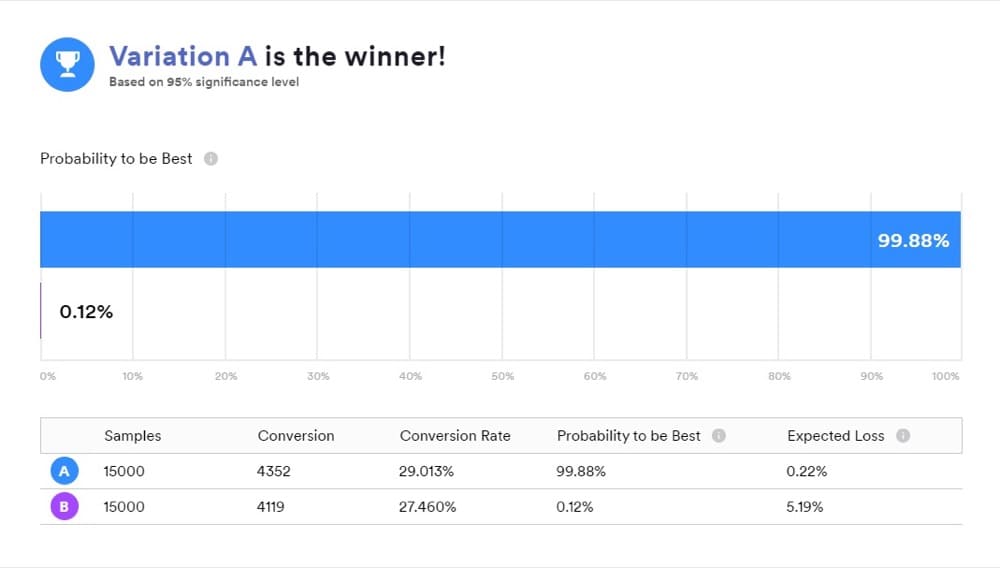
這是一種展示結果的便捷方式,但這不是您的測試所揭示的。 相反,您想要的答案是“A”和“B”的後驗比較。
以下是3種比較方法:
成為最好的概率 (P2BB)
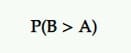
這是在貝葉斯 A/B 測試中宣布獲勝的概率。
具有最佳概率的變體是最有可能繼續優於另一個的變體。
這是從原始和挑戰者感興趣的度量的一組後驗樣本中計算出來的。
因此,例如,如果 B 最有可能提高您的轉化率,則 B 被宣佈為贏家。
預期提升
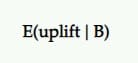
那麼,如果 B 是贏家,我們應該期待它有多大的提升呢? 它會繼續提供我們在測試中看到的相同結果嗎?
這就是預期提升試圖提供的洞察力。 給定一組後驗樣本,選擇 B 而不是 A 的預期提升被定義為百分比增加的可信區間(或平均值)。
在 A/B 測試中,我們通常將其作為挑戰者與控制者進行比較。 因此,如果挑戰者輸了,它會以負值(如 -11.35%)和正值(如 +9.58%)表示,如果它贏了。
預期損失
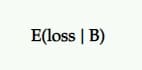
由於 B 不是 100% 的概率優於 A,因此如果您選擇 B 而不是 A,則有可能記錄損失。這表示為預期損失,就像預期的提升一樣,它由挑戰者反對控制的觀點。
它告訴您選擇 P2BB 變體的風險(即宣布的獲勝者)。
在我們深入神話之前,非常感謝分析傳奇人物 Georgi Georgiev。 他在 A/B 測試中對常客與貝葉斯推理以及貝葉斯概率和統計的深入分析啟發了下一節。
要避免的有關貝葉斯統計的神話
貝葉斯與頻率論者的爭論幾乎與不必要的一樣古老,因此已經收集了很多意見——並引發了很多神話。
A/B 測試工具供應商推廣這些神話(神話#2)中最大的一個,告訴你為什麼一種方法比另一種更好。
但是在閱讀了上面的部分之後,您會更好地了解。
讓我們揭示這些神話中的漏洞。
誤區一:貝葉斯主義者陳述他們的假設,頻率論者沒有
這表明貝葉斯以先驗分佈的形式做出假設,這些假設可供評估。 但是頻率論者會做出隱藏在數學中間的假設。
錯誤原因:貝葉斯主義者和頻率主義者做出了相似的基本假設,唯一的區別是貝葉斯主義者在數學之上做出了額外的假設。
頻率論模型在數學中使用假設,例如分佈的形狀、觀察結果的同質性或異質性以及觀察的獨立性。 而且它們並沒有隱藏。 事實上,它們在統計界得到了廣泛的討論,並在每一個常客統計測試中都有說明。
真相:頻率論者明確陳述他們的假設,並進一步測試假設:正態性檢驗、擬合優度檢驗(我們有樣本比率不匹配檢驗)等等。
神話#2。 貝葉斯方法給你你真正想要的答案
這裡的誤解是 p 值和置信區間不能告訴測試人員他們想知道什麼,而後驗概率和可信區間可以。 人們想知道諸如
- B 優於 A 的概率和
- 結果不是巧合的可能性。
P 值和假設檢驗(直接推理)不提供該信息,但反向推理提供。
為什麼會出錯:這是語言學的問題。 通常,當非統計學家使用“可能性”、“機會”和“概率”等術語時,他們並沒有考慮到它們的技術含義。 深入探究,你會發現他們對逆向推理和對直接推理一樣感到困惑。
根據 Georgi Georgiev 的說法,這樣的問題開始出現:
- “什麼是先驗概率? 它帶來了什麼價值?”
- “什麼是似然函數?”
- “什麼‘先驗’概率,我沒有先驗數據?”
- “我如何為先驗概率的選擇辯護?”
- “有沒有辦法在沒有任何這些混合的情況下傳達數據所說的內容?”
真相:應該更好地了解測試人員想知道什麼,而不是他們對技術術語的誤解。 P 值、置信區間和其他值可以告訴您收集的數據對結果的探測程度。 它們提供了一種確定性的衡量標準,不受主觀、未經檢驗的先前假設的影響。
誤區 3:貝葉斯推理比頻率推理更能幫助您傳達不確定性
因為測試的結果會產生更“有意義”的見解。
錯誤原因:頻率論和貝葉斯方法都有類似的工具來幫助您傳達確定性和 A/B 測試的結果。
| 頻率論者 | 貝葉斯 | ||||||||||
| ● 點估計 | ● 點估計 | ||||||||||
| ● P 值 | ● 可信區間 | ||||||||||
| ● 置信區間 | ● 貝葉斯因子 | ||||||||||
| ● P 值曲線 | ● 後驗分佈 (完成相同的任務 作為頻率曲線) | ||||||||||
| ● 置信曲線 | |||||||||||
| ● 嚴重性曲線等。 |
真相:這完全取決於你如何使用它們。 這兩種方法在傳達不確定性方面同樣有效。 但是,它們在表示不確定性度量的方式上存在差異。
神話#4。 貝葉斯 A/B 測試結果不受偷窺
一些貝葉斯統計學家認為,一旦看到“明顯的贏家”,就可以停止貝葉斯檢驗,這對最終結果幾乎沒有影響。
您可能知道這在頻率測試中是不可接受的,因此與貝葉斯相比,它被視為劣勢。 但真的是這樣嗎?
錯誤原因: Armitage 等人在 1969 年《皇家統計學會雜誌》上的一項題為“對累積數據的重複顯著性檢驗”的研究中。 展示了基於結果的可選停止如何增加錯誤概率。
當你注意到一個贏家時,你不能停下來,更新你的後驗,並將其用作你的下一個先驗,而不調整貝葉斯分析的工作方式。
真相:窺視對貝葉斯推理的影響與對頻率論的影響一樣大(如果你想做對的話)。
神話#5。 頻率統計是低效的,因為您必須等待固定的樣本量
CRO 社區的一些成員認為,頻率統計測試必須以固定的、預定的樣本量運行,否則結果無效。
結果,您等待的時間比獲得所需結果的時間更長。
為什麼它是錯誤的:頻率統計已經有大約七十年沒有被這樣使用了。 使用常客順序測試,您不需要固定的預定持續時間。
真相:今天更流行的順序測試需要最大樣本量來平衡 I 型和 II 型錯誤,但實際使用的樣本量因情況而異,具體取決於觀察到的結果。
那麼,您應該選擇貝葉斯還是頻率主義者? 兩者都有一個地方。
沒有必要選擇一方。 這兩種方法都有自己的位置。 例如,使用更新的先驗並需要快速結果的長期項目更適合貝葉斯方法。
另一方面,Frequentist 方法最適合需要在結果中有大量可重複性的項目。 例如在編寫許多擁有許多數據集的人會使用的軟件時。
正如穀歌決策智能負責人 Cassie Kozyrkov 所說,“統計是在不確定性下改變想法的科學”。
在她的貝葉斯與頻率統計摘要視頻中,她說:
“你可以將頻率論者和貝葉斯論者的辯論全部歸結為你正在改變主意的事情。 頻繁的人改變了他們對行動的看法,他們有一個首選的默認行動——也許他們沒有任何信念——但他們有一個他們在無知的情況下喜歡的行動,然後他們問:“我的證據 [或數據] 是否改變了我的想法?那個動作?” “根據我的證據,我覺得這樣做很荒謬嗎?”
另一方面,貝葉斯主義者以不同的方式改變主意。 他們從一個觀點開始,一個數學表達的個人觀點,稱為先驗,然後他們問,“在我納入一些證據後,我應該有什麼明智的觀點?” 因此,頻率主義者改變了他們對行動的看法,貝葉斯主義者改變了他們對信仰的看法。
根據你想如何制定決策,你可能更喜歡選擇一個陣營而不是另一個陣營。”
最後,我們都在走向相似的結論——不同之處在於這些結論是如何呈現給你的。
如果常客和貝葉斯推理是編程函數,輸入是統計問題,那麼兩者在返回給用戶的內容上會有所不同。 常客推理函數將返回一個數字,代表一個估計值(通常是一個匯總統計量,如樣本平均值等),而貝葉斯函數將返回概率。
摘自《黑客的概率編程和貝葉斯方法》一書
不太正確的是聲稱一個比另一個給出更多實際結果的說法。
關鍵要點
A/B 測試中的貝葉斯統計包括 4 個不同的步驟:
- 確定您的先前分佈
- 選擇一個反映您的信念的統計模型
- 運行實驗
- 使用結果更新您的信念併計算後驗分佈
您的結果將指向有洞察力的概率。 所以你會知道哪個變體最有可能成為最好的,你的預期損失和預期的提升。
大多數使用貝葉斯統計的 A/B 測試工具通常會為您解釋這些。 但是一個徹底的實驗者將進行測試後分析以更好地理解這些結果。
因為你已經做到了這一步,所以對你來說有一個有趣的事實:你知道每個人都熟悉的托馬斯貝葉斯的肖像嗎? 這個:

沒有人 100% 確定那是他。