I 型和 II 型错误：优化中不可避免的错误

当您在实验中错误地发现获胜者或未能发现它们时，就会发生 I 型和 II 型错误。 有了这两个错误，您最终会选择似乎可行或不可行的方法。 而不是真正的结果。

对测试结果的误解不仅会导致错误的优化工作，而且从长远来看还会使您的优化计划脱轨。

捕捉这些错误的最佳时机是在你犯错之前！ 因此，让我们看看如何在优化实验中避免遇到 I 型和 II 型错误。

但在此之前，让我们看一下原假设……因为是错误拒绝或不拒绝原假设导致 I 型和 II 型错误。

零假设：​H0

当您假设一个实验时，您不会直接跳到建议提议的更改将移动某个指标。

您首先说提议的更改根本不会影响相关的指标——它们是不相关的。

这是您的零假设 (H0)。 H0 始终表示没有变化。 默认情况下，这就是您所相信的……直到（并且如果）您的实验证明了它。

您的替代假设（Ha 或 H1）是存在积极变化。 H0 和 Ha 在数学上总是对立的。 Ha 是您期望提议的更改产生影响的那个，它是您的替代假设 - 这就是您正在通过实验测试的内容。

因此，例如，如果您想在定价页面上运行一个实验并向其中添加另一种付款方式，您首先会形成一个零假设，即：额外的付款方式不会对销售产生影响。 你的替代假设是：额外的付款方式将增加销售额。

事实上，进行实验是在挑战零假设或现状。

当您错误地拒绝或未能拒绝原假设时，就会发生 I 型和 II 型错误。

了解 I 类错误

I 类错误称为误报或 Alpha 错误。

在假设检验的 I 类错误实例中，您的优化测试或实验 *似乎是成功的 *并且您（错误地）得出结论，您正在测试的变体与原始版本不同（更好或更差）。

在第一类错误中，你会看到上升或下降——这只是暂时的，不太可能长期维持——最终会拒绝你的原假设（并接受你的替代假设）。

错误地拒绝零假设可能有多种原因，但最主要的原因是偷看（即，在中间或实验仍在运行时查看您的结果）。 并在达到设定的停止标准之前调用测试。

许多测试方法不鼓励偷看的做法，因为查看中间结果可能会导致错误的结论，从而导致 I 类错误。

以下是你如何犯 I 类错误：

假设您正在优化 B2B 网站的登录页面，并假设向其添加徽章或奖励会减少潜在客户的焦虑，从而提高表单填写率（导致更多潜在客户）。

因此，您对该实验的零假设变为：添加徽章对表单填写没有影响。

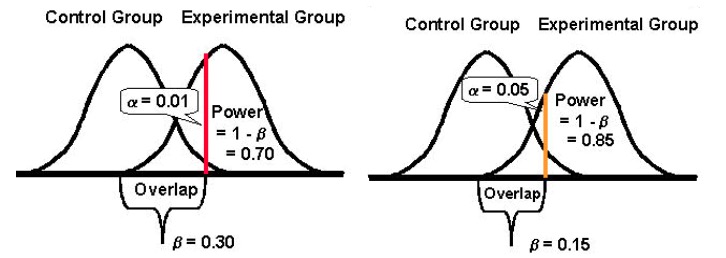
这种实验的停止标准通常是某个时期和/或在 X 转换发生在设定的统计显着性水平之后。 传统上，优化器会尝试达到 95% 的统计置信度标记，因为它使您有 5% 的机会出现对于大多数优化实验而言被认为足够低的 I 类错误。 一般来说，这个指标越高，犯第一类错误的机会就越低。

您所追求的置信水平决定了您出现 I 类错误 (α) 的概率。

因此，如果您的目标是 95% 的置信水平，您的 α 值将变为 5%。 在这里，你承认你的结论有 5% 的可能性是错误的。

相比之下，如果您的实验置信度为 99%，那么您出现 I 类错误的概率会下降到 1%。

假设，对于这个实验，您太不耐烦了，而不是等待实验结束，您只需一天就查看测试工具的仪表板（偷看！）。 您会注意到“明显”的提升——您的表单填写率以 95% 的置信水平上升了 29.2%。

和巴姆…

……你停止你的实验。

…拒绝零假设（徽章对销售没有影响）。

…接受替代假设（徽章促进销售）。

......并运行带有奖项徽章的版本。

但是，当您衡量一个月内的潜在客户时，您会发现该数字几乎与您使用原始版本报告的数字相当。 毕竟，徽章并不重要。 并且零假设可能被徒劳地拒绝了。

这里发生的情况是，你过早地结束了实验，拒绝了原假设，最终得到了一个错误的赢家——犯了 I 类错误。

避免实验中的 I 类错误

降低您遇到 I 类错误的机会的一种可靠方法是提高置信水平。 5% 的统计显着性水平（转化为 95% 的统计置信水平）是可以接受的。 这是一个大多数优化器都会安全地做出的赌注，因为在这里，你会在不太可能的 5% 范围内失败。

除了设置高置信度之外，运行足够长时间的测试也很重要。 测试持续时间计算器可以告诉您必须运行测试多长时间（在考虑到指定的效果大小等因素之后）。 如果您让实验按预期进行，您会显着降低遇到类型 1 错误的机会（假设您使用的是高置信度）。 等到您获得具有统计意义的结果可确保您错误地拒绝原假设并犯下 I 类错误的可能性很小（通常为 5%）。 换句话说，使用良好的样本量，因为这对于获得具有统计意义的结果至关重要。

现在这都是关于与实验中的置信度（或显着性）相关的 I 型错误。 但是还有另一种类型的错误也会潜入你的测试——II 型错误。

了解 II 类错误

II 类错误称为假阴性或 Beta 错误。

与 I 类错误相比，在 II 类错误的情况下，实验*似乎不成功（或不确定）*并且您（错误地）得出结论，您正在测试的变体与原来的。

在 II 型错误中，您看不到真正的上升或下降，最终无法拒绝原假设并拒绝备择假设。

以下是你如何犯第二类错误：

从上面回到同一个 B2B 网站……

因此，假设这次您假设在表单顶部显着添加 GDPR 合规免责声明将鼓励更多潜在客户填写（导致更多潜在客户）。

因此，您对此实验的零假设变为： GDPR 合规性免责声明不会影响表单填写。

相同的替代假设是： GDPR 合规性免责声明导致更多的表格填写。

如果存在任何偏差，测试的统计能力决定了它可以检测到原始版本和挑战者版本的性能差异的能力。 传统上，优化器试图达到 80% 的统计功效标记，因为该指标越高，出现 II 型错误的机会就越低。

统计功效取一个介于 0 和 1 之间的值（通常以 % 表示）并控制您的 II 型错误 (β) 的概率； 它的计算公式为：1 – β

测试的统计功效越高，遇到 II 类错误的概率就越低。

因此，如果一个实验的统计功效为 10%，那么它很容易受到 II 型错误的影响。 然而，如果一个实验的统计功效为 80%，那么它犯 II 类错误的可能性就会小得多。

同样，您运行测试，但这次您没有注意到表单填写有任何显着提升。 两个版本都报告了接近相似的转化率。 因此，您将停止实验并继续使用原始版本，而无需遵守 GDPR 合规性免责声明。

然而，当您深入研究实验期间的潜在客户数据时，您会发现虽然两个版本（原始版本和挑战者）的潜在客户数量似乎相同，但 GDPR 版本确实让您的数量有了很好的显着上升来自欧洲的线索。 （当然，您可以使用受众定位来仅向来自欧洲的潜在客户展示该实验——但这是另一回事。）

这里发生的情况是你过早地结束了测试，没有检查你是否获得了足够的力量——犯了第二类错误。

避免实验中的 II 型错误

为避免 II 类错误，请运行具有高统计功效的测试。 尝试配置您的实验，以便您可以达到至少 80% 的统计功效标记。 对于大多数优化实验来说，这是一个可接受的统计功效水平。 有了它，您可以确保至少在 80% 的情况下，您将正确拒绝错误的零假设。

为此，您需要查看增加它的因素。

其中最大的是样本量（给定观察到的效应量）。 样本量直接关系到检验的功效。 巨大的样本量意味着高功效测试。 动力不足的测试非常容易受到 II 类错误的影响，因为您检测到挑战者和原始版本结果差异的机会大大降低，尤其是对于低 MEI（更多信息见下文）。 因此，为避免 II 类错误，请等待测试积累足够的功率以最大限度地减少 II 类错误。 理想情况下，对于大多数情况，您希望达到至少 80% 的功率。

另一个因素是您为实验设定的最小感兴趣效应 (MEI) 。 MEI（也称为 MDE）是您希望在相关 KPI 中检测到的最小差异幅度。 如果您设置较低的 MEI（例如，关注 1.5% 的提升），则遇到 II 型错误的机会会增加，因为检测小的差异需要更大的样本量（以获得足够的功效）。

最后，重要的是要注意，犯 I 类错误的概率 (α) 和犯 II 类错误的概率 (β) 之间往往存在反比关系。 例如，如果您降低 α 的值以降低犯 I 类错误的概率（假设您将 α 设置为 1%，意味着置信水平为 99%），则您的实验的统计功效（或其能力，β ，当存在差异时检测到差异）最终也会减少，从而增加您出现 II 型错误的可能性。

更容易接受任何一种错误：I型和II型（并取得平衡）

降低一种错误的概率会增加另一种错误的概率（假设所有其他内容保持不变）。

因此，您需要决定您可以更容忍的错误类型。

一方面，犯 I 类错误并为所有用户推出更改可能会花费您的转化和收入——更糟糕的是，也可能成为转化杀手。

另一方面，如果犯了 II 类错误，并且未能为所有用户推出成功的版本，可能会再次使您失去原本可以赢得的转化。

总是，这两个错误都是有代价的。

但是，根据您的实验，您可能会比另一种更容易接受。 一般来说，测试人员发现第一类错误比第二类错误严重四倍。

如果您想采取更平衡的方法，统计学家 Jacob Cohen 建议您应该选择 80% 的统计功效，同时“在 alpha 和 beta 风险之间取得合理的平衡”。 ”（80% 的功率也是大多数测试工具的标准。）

而就统计显着性而言，标准设定为95%。

基本上，这都是关于妥协和你愿意容忍的风险水平。 如果您想真正最小化这两种错误的可能性，您可以选择 99% 的置信度和 99% 的功效。 但这意味着您将在看似永恒漫长的时期内使用不可能巨大的样本量。 此外，即使那样你也会留下一些错误的余地。

每隔一段时间，你就会错误地结束一个实验。 但这是测试过程的一部分——掌握 A/B 测试统计数据需要一段时间。 调查和重新测试或跟进您成功或失败的实验是重申您的发现或发现您犯了错误的一种方法。