Python 上的单神经元神经网络——具有数学直觉

让我们构建一个简单的网络——非常简单，但是一个完整的网络——只有一层。 只有一个输入——一个神经元（也是输出），一个权重，一个偏差。

我们先运行代码，然后逐个分析

克隆 Github 项目，或者在您喜欢的 IDE 中简单地运行以下代码。

如果您在设置 IDE 时需要帮助，我在此处描述了该过程。

如果一切顺利，您将获得以下输出：

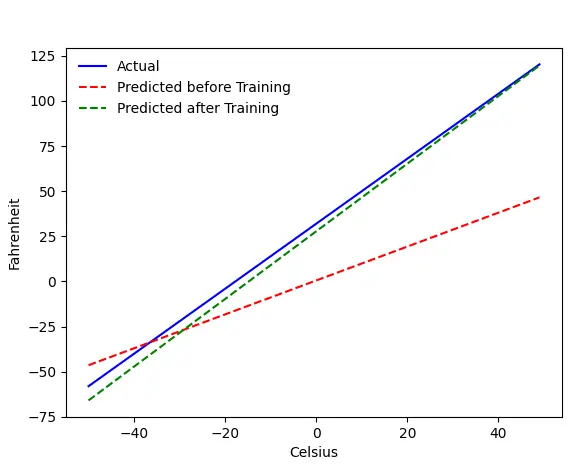
问题——摄氏华氏度

我们将训练我们的机器从摄氏温度预测华氏温度。 正如您从代码（或图表）中可以理解的那样，蓝线是实际的摄氏-华氏关系。 红线是我们的婴儿机器在没有任何训练的情况下预测的关系。 最后我们训练机器，绿线是训练后的预测。

查看第 65–67 行——在训练之前和之后，它使用相同的函数（ get_predicted_fahrenheit_values() ）进行预测。 那么神奇的 train() 在做什么呢？ 让我们来了解一下。

网络结构

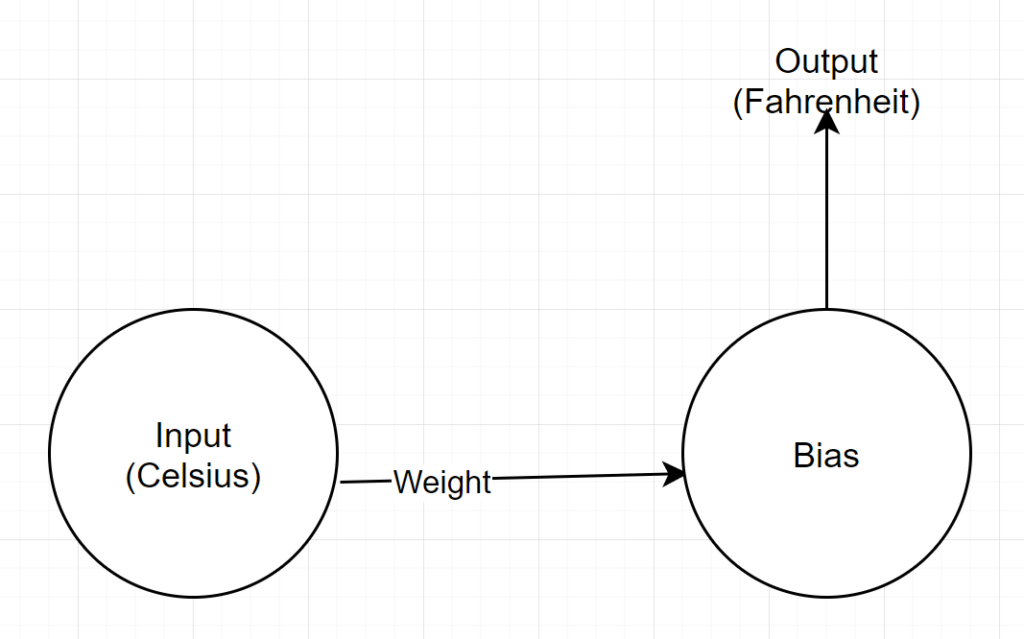
输入：代表摄氏度的数字

重量：代表重量的浮点数

偏差：代表偏差的浮点数

输出：代表预测华氏温度的浮点数

所以，我们总共有 2 个参数——1 个权重和 1 个偏差

代码分析

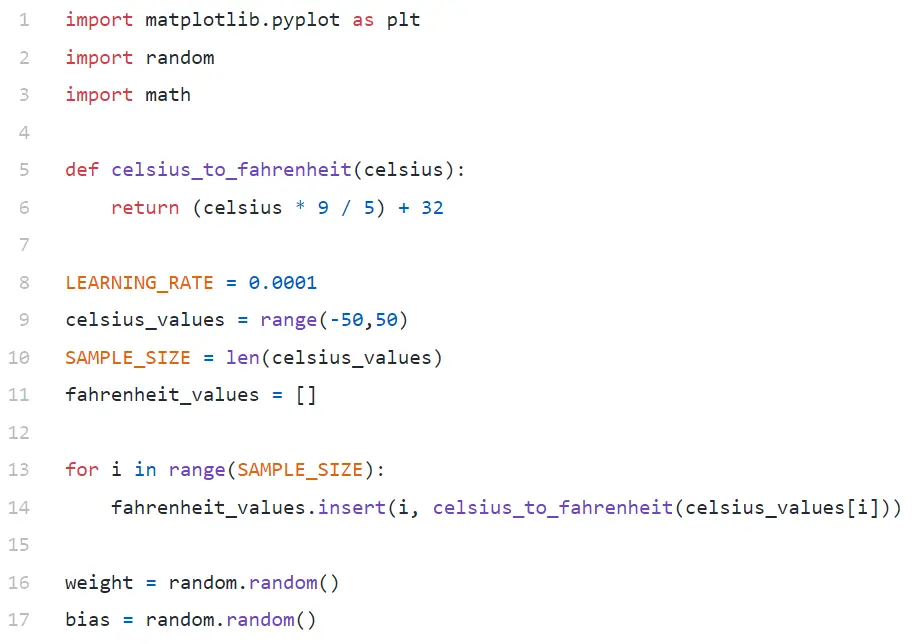
在第 9 行中，我们生成了一个包含 -50 和 +50 之间的 100 个数字的数组（不包括 50 — range 函数不包括上限值）。

在第 11-14 行中，我们为每个摄氏度值生成华氏度。

在第 16 行和第 17 行，我们正在初始化权重和偏差。

火车（）

我们在这里运行 10000 次训练迭代。 每次迭代由以下部分组成：

1. 向前（第 57 行）传球
2. 向后（第 58 行）传球
3. 更新参数（第 59 行）

如果你是 python 新手，你可能会觉得有点奇怪——python 函数可以返回多个值作为tuple 。

请注意， update_parameters是我们唯一感兴趣的东西。我们在这里所做的其他一切都是评估这个函数的参数，它们是我们的权重和偏差的梯度（我们将在下面解释梯度是什么）。

1. grad_weight：表示权重梯度的浮点数
2. grad_bias：表示偏差梯度的浮点数

我们通过向后调用获得这些值，但它需要输出，我们通过在第 57 行调用向前获得。

向前（）

请注意，这里celsius_values和fahrenheit_values是 100 行的数组：

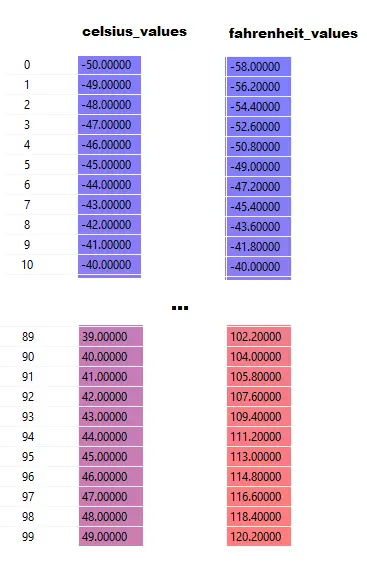
执行第 20–23 行后，对于摄氏值，例如 42

输出 = 42 * 权重 + 偏差

因此，对于celsius_values中的 100 个元素，输出将是每个对应的 celsius 值的 100 个元素的数组。

第 25-30 行使用均方误差 (MSE) 损失函数计算损失，它只是所有差异平方除以样本数（在本例中为 100）的一个花哨名称。

小损失意味着更好的预测。 如果您在每次迭代中保持打印损失，您将看到它随着训练的进行而减少。

最后，在第 31 行，我们返回预测的输出和损失。

落后

我们只对更新我们的权重和偏差感兴趣。 要更新这些值，我们必须知道它们的梯度，这就是我们在这里计算的。

注意梯度是按相反的顺序计算的。 首先计算输出的梯度，然后计算权重和偏差，因此得名“反向传播”。 原因是，为了计算权重和偏差的梯度，我们需要知道输出的梯度——这样我们就可以在链式法则公式中使用它。

现在让我们看看什么是梯度和链式法则。

坡度

为简单起见，假设我们只有一个值celsius_values和fahrenheit_values ，分别为42和107.6 。

现在，第 30 行中的计算分解变为：

损失 = (107.6 — (42 * 权重 + 偏差))² / 1

如您所见，损失取决于两个参数——权重和偏差。 考虑重量。 想象一下，我们用一个随机值初始化它，比如 0.8，在评估上面的等式后，我们得到 123.45 作为loss的值。 根据这个损失值，您必须决定如何更新体重。 你应该把它设为 0.9 还是 0.7？

您必须以某种方式更新权重，以便在下一次迭代中获得较低的损失值（请记住，最小化损失是最终目标）。 所以，如果增加体重增加了损失，我们就会减少它。 如果增加体重会减少损失，我们会增加它。

现在的问题是，我们如何知道增加权重会增加还是减少损失。 这就是渐变的用武之地。 从广义上讲，梯度是由导数定义的。 请记住，从您的高中微积分中，∂y/∂x（它是 y 相对于 x 的偏导数/梯度）表示 y 将如何随着 x 的微小变化而变化。

如果 ∂y/∂x 为正数，则意味着 x 的小幅增量将增加 y。

如果 ∂y/∂x 为负数，则意味着 x 的小幅增量会减小 y。

如果 ∂y/∂x 很大，那么 x 的微小变化就会导致 y 的巨大变化。

如果 ∂y/∂x 很小，x 的微小变化会导致 y 的微小变化。

因此，从梯度中，我们得到 2 个信息。 参数必须更新的方向（增加或减少）以及多少（大或小）。

链式法则

通俗地说，链式法则说：

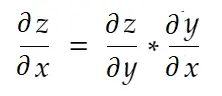
考虑上面重量的例子。 我们需要计算grad_weight来更新这个权重，计算公式为：

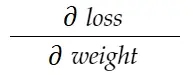
使用链式法则公式，我们可以推导出它：

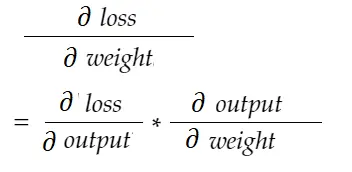
同样，偏差梯度：

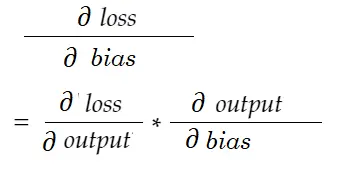
让我们画一个依赖关系图。

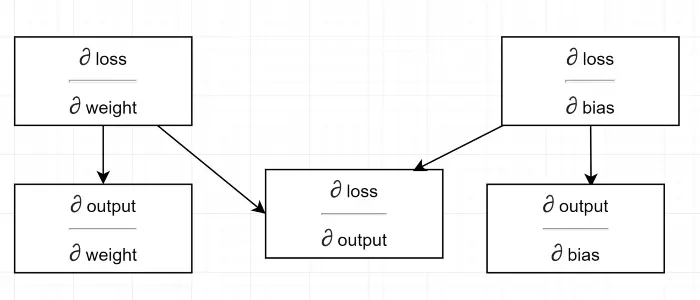
查看所有计算取决于输出的梯度（∂损失/∂输出） 。 这就是为什么我们首先在回传中计算它（第 34-36 行）。

事实上，在高级 ML 框架中，例如在 PyTorch 中，您不必为回传编写代码！ 在前向传播过程中，它创建计算图，在反向传播过程中，它通过图中的相反方向并使用链式法则计算梯度。

∂损失/∂输出

我们在代码中通过grad_output定义这个变量，我们在第 34-36 行计算。 让我们找出我们在代码中使用的公式背后的原因。

请记住，我们将机器中的所有 100 个celsius_values一起输入。 因此， grad_output 将是一个包含 100 个元素的数组，每个元素包含celsius_values中相应元素的输出梯度。 为简单起见，让我们考虑一下， celsius_values中只有 2 个项目。

所以，分解第 30 行，

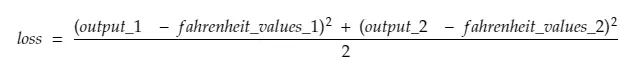
在哪里，

output_1 = 第一个摄氏度值的输出值

output_2 = 第二摄氏度值的输出值

fahreinheit_values_1 = 1 摄氏度值的实际华氏温度值

fahreinheit_values_1 = 第二摄氏度值的实际华氏度值

现在，结果变量 grad_output 将包含 2 个值 - output_1 和 output_2 的梯度，这意味着：

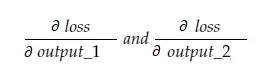
让我们只计算 output_1 的梯度，然后我们可以对其他的应用相同的规则。

微积分时间！

这与第 34-36 行相同。

权重梯度

想象一下，我们在 celsius_values 中只有一个元素。 现在：

这与第 38-40 行相同。 对于 100 celsius_values，将汇总每个值的梯度值。 一个明显的问题是我们为什么不按比例缩小结果（即除以 SAMPLE_SIZE）。 由于我们在更新参数之前将所有梯度乘以一个小因子，因此没有必要（参见最后一节更新参数）。

偏置梯度

这与第 42 行相同。 与权重梯度一样，100 个输入中的每一个的这些值都被求和。 同样，这很好，因为在更新参数之前梯度乘以一个小因子。

更新参数

最后，我们正在更新参数。 请注意，梯度在减去之前乘以一个小因子（LEARNING_RATE），以使训练稳定。 LEARNING_RATE 的大值会导致过冲问题，而极小的值会使训练变慢，这可能需要更多的迭代。 我们应该通过反复试验找到它的最佳值。 上面有很多在线资源，包括这个，以了解更多关于学习率的信息。

请注意，我们调整的确切数量并不是非常关键。 例如，如果您稍微调整 LEARNING_RATE， descent_grad_weight和descent_grad_bias变量（第 49-50 行）将被更改，但机器可能仍然工作。 重要的是确保这些数量是通过使用相同因子（在本例中为 LEARNING_RATE）按比例缩小梯度得出的。 换句话说，“保持梯度下降成比例”比“下降多少”更重要。

另请注意，这些梯度值实际上是为 100 个输入中的每一个评估的梯度的总和。 但由于这些是用相同的值缩放的，所以如上所述。

为了更新参数，我们必须用 global 关键字声明它们（在第 47 行）。

从这往哪儿走

通过以pythonic方式用列表理解替换for循环，代码会小得多。 现在看一下 - 不会花费超过几分钟的时间来理解。

如果您到目前为止了解了所有内容，那么现在可能是了解具有多个神经元/层的简单网络内部结构的好时机——这是一篇文章。