正态分布——没有数学的直观介绍

我会尽量让这篇文章远离方程式和满口的行话。 但是，我需要你至少具备以下能力：

• 能够解释简单的图表。
• 概率的初级知识。 你至少明白，如果我抛硬币，正面的概率是 50%。
• 积分学和量子物理学（开玩笑！）

为什么是正态分布

理解某事的一种直观方法是调查为什么需要它。 让我们为正态分布（也称为高斯分布）做这件事。

假设你有一个有趣的习惯。 每天你掷硬币 100 次。 预期你会得到 50 次正面（或接近 50 次）是“正常的”。 很少有好的日子——你可能会得到大约 55 次，很少超过 65 次。

现在，您想量化这种“稀有性”。 因此，您开始记录每天获得头部的次数。

一年中每天的人头数

下面是一年（365天）之后的数据——第一个是你第一天得到的正面数，最后一个是你最后一天得到的正面数。 您不需要检查下面的所有数字，但很容易发现它们中的大多数都在 50 左右。

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

使用直方图更好地可视化

让我们根据上面的数据绘制一个直方图：

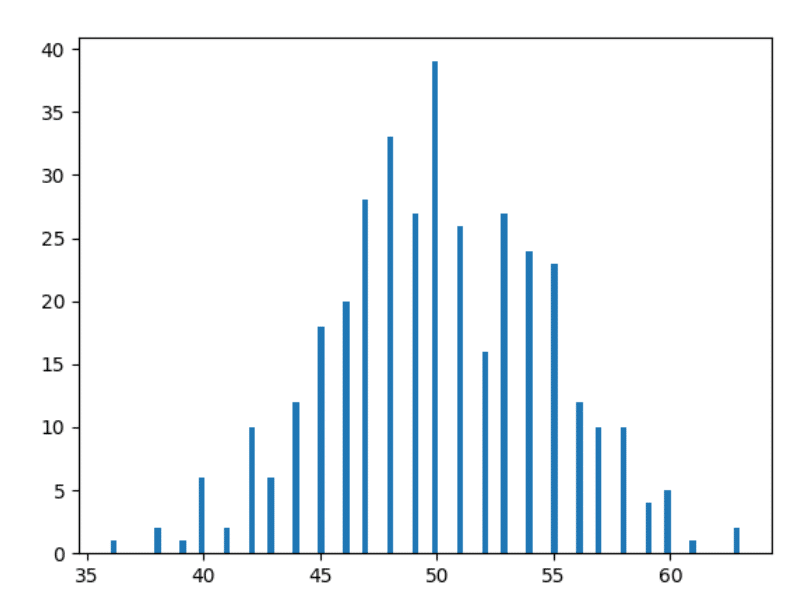
啊哈！ 当你在谷歌上搜索“正态分布”时，它看起来不像你在互联网上看到的图像吗？ 我们就快到了！

因此，如果您不了解直方图 - 我们刚刚在此处绘制了我们获得特定头部计数的天数。 例如，我们在一年中的 2 个特定日子里获得了 36 次正面（如果你不相信我，请查看上面的数据），这就是为什么在 36 的水平点上有一个高度为 2 单位的条（红色下图中左侧的矩形）。

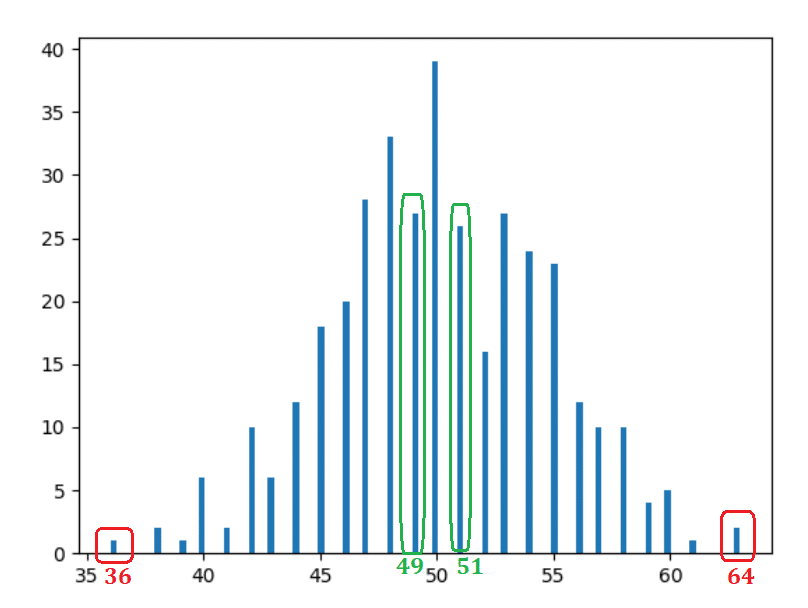
观察

1. 非常明显和意料之中——大多数时候出现了 50 个正面。
2. 我们离中心（50）越远，发生率大多在减少。
3. 相同距离的条形具有相似的形状。 例如，如果您将一个单位向左 (49) 或向右 (51) 移动 - 出现相似 - 分别为 30 和 31（绿色矩形）。 如果您向左 (36) 或向右 (64) 移动 14 个单位，出现的次数再次相似 — 分别为 2 和 1（红色矩形）。

10年数据

现在让我们快进一点——绘制 10 年的数据。

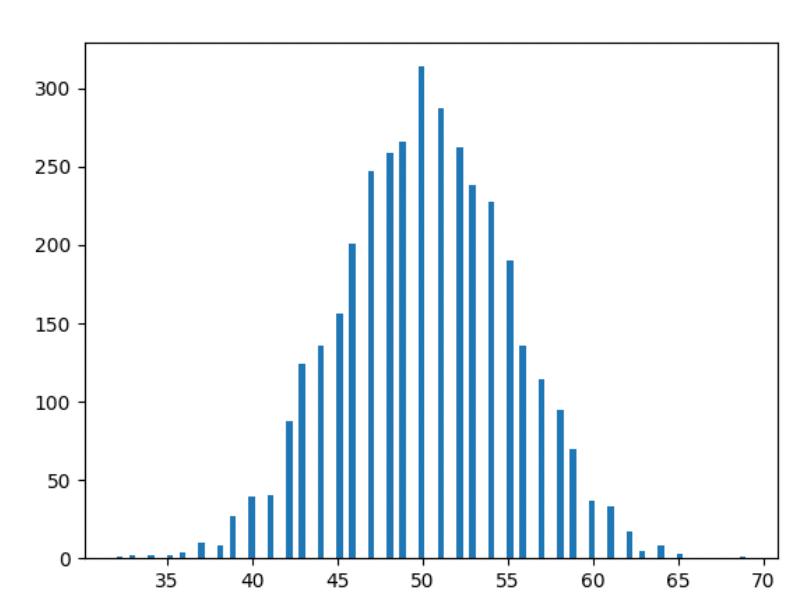
1000年数据

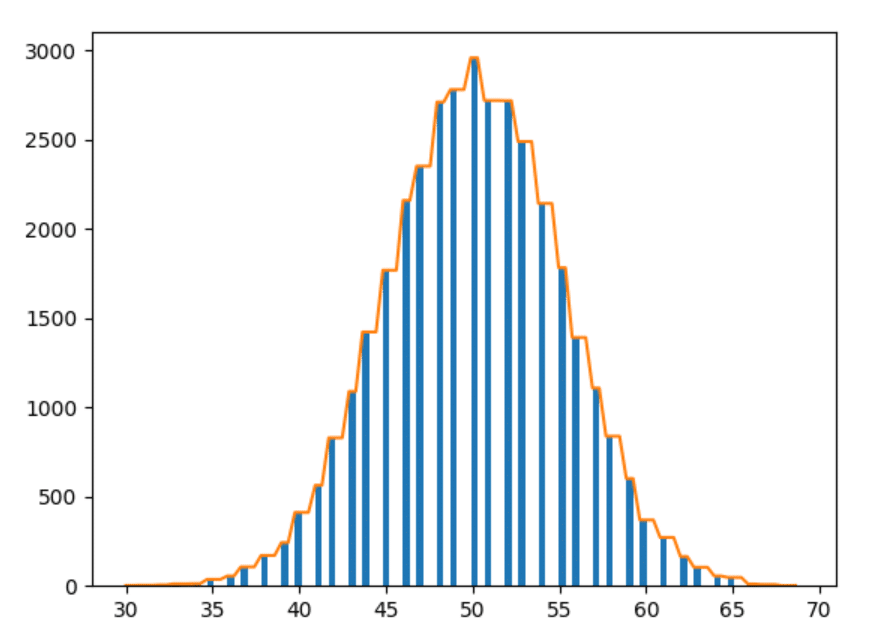
好的——最后一个。 让我们绘制 1000 年的数据。

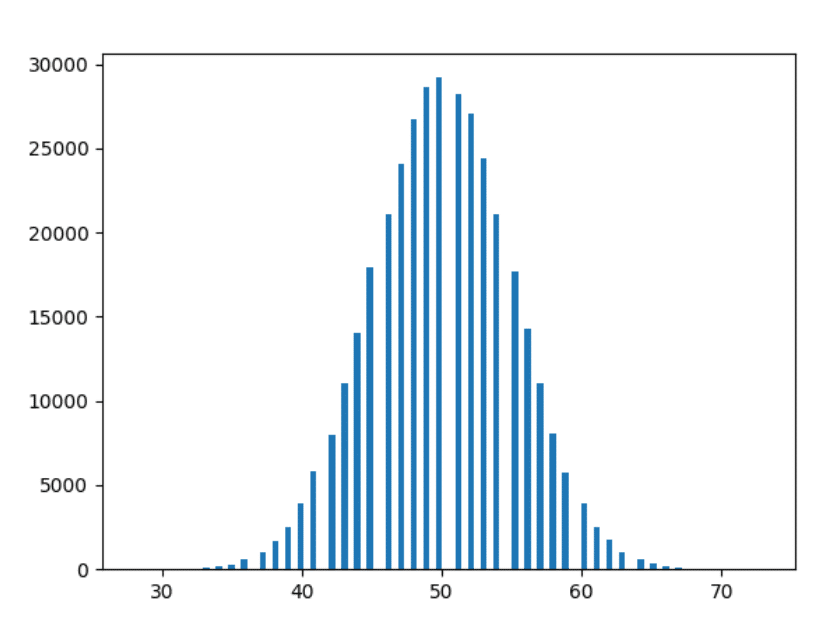
观察

1. 我们实验得越多，形状就越平滑。
2. 我们进行的实验越多，条形图遵循上述观察的越多（即，相似距离的条形图呈现更接近的形状）。

该死的正态分布在哪里

好的——背景太多了——现在让我们进入正题。

让我们看看谷歌给出的答案：

这个定义中有几件事：

随机变量：简单地说——随机变量是随机实验的一组可能值，比如抛硬币。 在我们的示例中，我们实验的可能值是Head或Tail 。

钟形：您是否注意到我们的直方图呈钟形？

对称：相同距离的条形具有相似的形状——不是对称的吗？

因此，正态分布代表了抛硬币等事件的结果分布——分布倾向于保持一些属性，包括对称性和钟形。

除了抛硬币，还有哪些现象服从正态分布？

这里有一些很酷的例子。

• 人口身高——更多人属于平均身高组。 极高或极矮的人很少见。 而且发现极高和极矮的机会几乎相等。
• 掷骰子
• 鞋号
• 智商
• 还有很多其他……

这些现象是否严格服从正态分布？

简单回答是不。 虽然，正如我们在上面看到的——你实验得越多，数据就越符合正态分布特性。 但不能保证无论如何都不会发生一些不太可能发生的事件。

宇宙中的所有概率分布都是正态分布吗？

不，有许多现象是由其他某种分布决定的。

• 给定数量的顾客到达、电话、事故、体育赛事和洪水的概率遵循泊松分布。
• 对于企业销售而言，一家公司 20% 的客户负责 80% 的销售额。 （帕累托分布）
• 城市交通模式——指数分布
• 从一群女孩和男孩中随机选择一个团队的成员——超几何分布

还有很多 …

我只是通过谷歌搜索“现实生活中的例子”和这里列出的一些发行版来制作上面的列表——并不是说我理解所有这些。 😉

为什么某些自然现象倾向于服从正态分布是有原因的吗

是的——引用我最喜欢的解释：

通常的解释是正态分布的另一个名称，即“误差分布”。 这个想法是错误通常是随机的，因此它们朝一个方向发展的可能性与朝另一个方向发展的可能性一样大。 例如，射手可能会向左射击一点，向右射击一点，或者高一点射击低一点。 因此，射击距离靶心多远的图表将反映这种随机趋势，并且围绕平均值对称。 同样，对于身高和智力——许多基因（可能有数千个）促成了这些结果，许多环境因素也是如此，例如营养、疾病、低收入等等。

正态分布参数

如果你对到目前为止的讨论有直觉 - 你已经是赢家了。 任务完成。 文章的其余部分是一个奖励。

您看到的所有正态分布图的形状都不同。 他们中的一些人比其他人更平坦。 他们中的一些人有很好的身高。 所有这些形状仅由 2 个参数控制：

意思是

平均值由平均值定义。 它定义了钟的高度。 对于掷硬币的例子，平均值接近 50，这是图中的顶部位置。

标准差

因为我保证这篇文章不会使用方程式，所以我不会在这里给出它的数学表示。 但无论如何，这并不难。 标准差是表示数据多样性的指标。

例如，托儿所的年龄标准差将低于足球俱乐部的年龄标准差，因为足球俱乐部中最年轻和最年长的群体之间的年龄差距应该大得多。

标准偏差决定了曲线的宽度。 较小的标准偏差会产生陡峭的曲线，而较大的标准偏差会产生更平坦的曲线。