用你的编程意识感受微积分

我相信会编程的人——有能力理解比微积分更复杂的概念。 有许多才华横溢的程序员仍在为微积分苦苦挣扎的一个原因并不是它很难。 这主要是因为我们以错误的方式教授它（以及许多其他主题）。

如果你在生活中做过一些编码——甚至是一些玩具练习，比如生成素数，你可能已经做过类似的事情，这些事情发生在微积分中，但从来没有机会联系起来。

写这篇文章的目的既不是教你微积分也不是编程——而是帮助你连接一些点。

我将在一分钟后进入编码部分。 但请允许我在此之前简要介绍一下背景。

变化率

微积分谈论“变化率”。 让我们试着理解这意味着什么。

对于变量 (x) 的变化，函数的变化率就是函数的变化除以 x 的变化。 让我们用实际数字可视化：

考虑 2 个点 x=2 和 x=6，以及函数 y=f(x) = x²。

另外，考虑dx = x 轴上这两个点之间的距离。 dy是这些 x 值的 y 值之间的距离。

那么，y 从 x=2 到 x=6 的变化率是

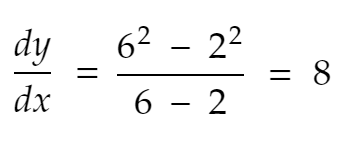
衍生物

现在——导数 dy/dx 是 x 的无限小的变化时 y 的变化率。 由于这个距离 (6–2=4) 不是无限小——甚至不是很近，我们不能将上述方程称为导数。 所以，现在让我们选择一个较小的数字， 0.1 。

当 x = 0 时，y = x² = 0² = 0。

正方向的最近邻，x = 0.1。 y 变为 0.1² = 0.01。

所以，

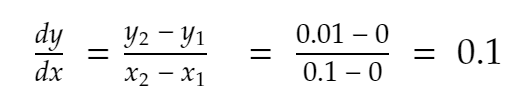
让我们再试一次。 0.1 到正方向的最近邻，x = 0.2。 因此，y 变为 0.2² = 0.04。 所以，

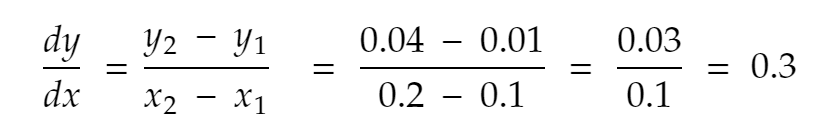
如果我们再重复这个过程几次，这就是我们得到的：

如果你想玩它，这里是 excel 文件。

在我们的上下文中， dx （这是我们虚构的 x 轴上 2 个相邻点之间的无限小距离）是 0.1。

x相应增加。

y就是 x²。

dy是 2 个相邻 y 值之间的距离。 例如，当 x= 0.1 时，当前 y (0.01 ) 和下一个 y (0.04) 之间的距离为 0.03 — 因此，在 x=0.1 时 dy 为 0.03。

dy/dx是 dy 除以 dx。

dy/dx / x是 dy/dx 除以 x。

现在请注意，随着 x 的增加，最后一行接近 2，这意味着 — x² 相对于 x 的变化率接近 x 的两倍，即2x 。

还记得 x² 关于 x 的导数吗？ 2倍！ 找到一些联系？

编码时间

让我们尝试一下我们迄今为止讨论过的代码。

假设您已经安装了 Python，在终端中运行：

之后，运行以下 Python 代码：

这里：

x ：包含从 0 到 9 的数字。

y : 另一个数组，每个元素都是对应 x 元素的平方

dy ：另一个用零初始化的数组。 我们将把 y 距离放在这个数组中。

dydx ：另一个用零初始化的数组。 它将包含每个点的 dy/dx 值。

dx ：很明显——它是步长。 2 个连续数字之间的距离，随着 SIZE 的增加而减小。 如果 SIZE = 10，dx = 1。如果 SIZE = 100，dx = 0.1。

首先，我们为每个点推导 dy。 然后我们从中计算 dydx。

请注意：

在这里，我们省略了第一个和最后一个值。 x 的第一个值为 0，这将产生零除错误。 而且我们无法计算 dy/dx 的最后一个值，因为我们没有 dy 的最后一个值——因为它需要 y 的最后一个可用值，而我们这里没有。

如果一切顺利，你会得到这个图表：

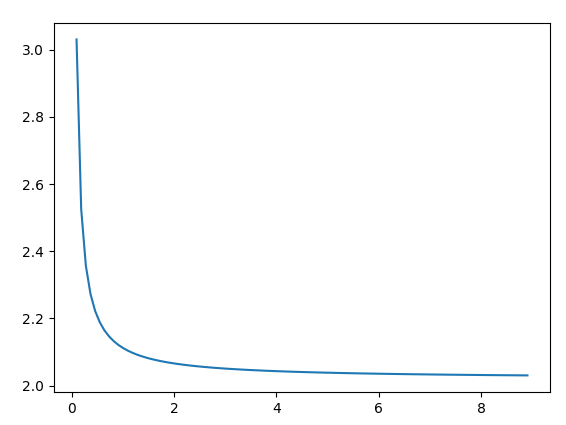
你从剧情中了解到的

如您所见，图表正在接近 2。增加 SIZE 的值（意味着将 dx 设置得更低）并查看图表如何更快地接近 2。

二阶导数

既然您已经走到了这一步，只需再执行几个步骤即可实现二阶导数，这将使您对任意阶的导数有了直觉。

如您所知，二阶导数是一阶导数相对于 x 的变化率。 简单地说——二阶导数中的 dy/dx 就像一阶导数中的 y。

让我们对上面的代码做如下修改：

再声明 2 个数组：

d2ydx2 ：这将代表二阶导数：

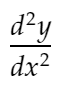
distance_dydx：表示 2 个相邻点之间 dy/dx 值之间的距离

这是二阶导数的完整代码：

在 for 循环中计算 dydx 后，我们执行另一个循环来计算二阶导数。 通过一些明智的编码，我们可以在同一个循环中计算二阶导数（尝试作为练习）——但为了清楚起见，我在这里将它们分开。

另外，请注意：

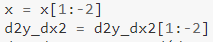
正如我们在一阶导数中所做的那样，我们也在这里省略了一些值。 最后两个值被省略，因为倒数第二个需要最后一个“一阶导数”值，我们无法计算（因为我们没有所需的 y 值——如上所述）。 这是否意味着在三阶导数的情况下我们必须省略最后 3 个值？🤔 - 那是你自己找的。

这是输出图：

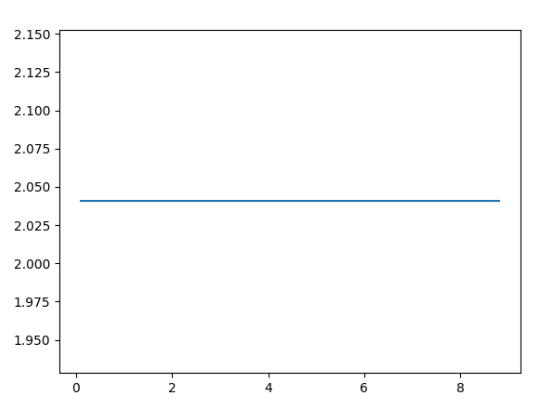
我们在这里看到了什么？

高中时就知道：

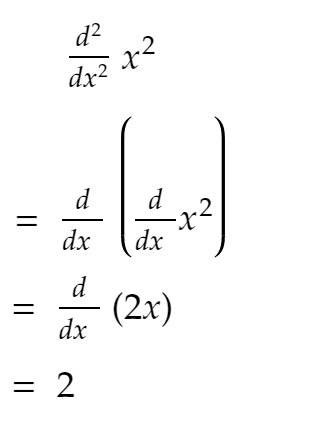
现在，正如您从上面的代码中看到的那样，二阶导数大部分保持不变，如果您继续增加 SIZE — 它接近 2！

为什么变化率很重要

你可能想知道：

——我们为什么要经历所有这些讨厌的麻烦？ 我们从变化率或导数中得到什么有用的信息？

— 为什么我们不能随随便便的变化率而变化？ 为什么只有无限小？ 我们从关于无穷小的变化率中得到什么信息，而这些信息不能从关于较大值的变化率中找到？

——这个无限小的东西有点像黑客？ 我们处理了一些上面的小数字，但实际上肯定不是无限小。

如果我允许自己继续下去，你会看到这篇文章的长度走开，不会走到这一步。 也许改天我们会解决这些问题😀。