Tip I ve Tip II Hatalar: Optimizasyonda Kaçınılmaz Hatalar

Tip I ve tip II hatalar, deneylerinizde yanlışlıkla kazananları tespit ettiğinizde veya onları tespit edemediğinizde meydana gelir. Her iki hatada da işe yarayıp yaramadığına karar verirsiniz. Ve gerçek sonuçlarla değil.

Test sonuçlarının yanlış yorumlanması yalnızca yanlış yönlendirilmiş optimizasyon çabalarıyla sonuçlanmaz, aynı zamanda uzun vadede optimizasyon programınızı rayından çıkarabilir.

Bu hataları yakalamak için en iyi zaman, onları yapmadan önce! Şimdi, optimizasyon denemelerinizde tip I ve tip II hatalarıyla karşılaşmaktan nasıl kaçınabileceğinizi görelim.

Ama ondan önce, boş hipoteze bakalım… çünkü tip I ve tip II hatalara neden olan boş hipotezin hatalı olarak reddedilmesi veya reddedilmemesidir .

Sıfır Hipotezi: ​H0

Bir denemeyi varsaydığınızda, önerilen değişikliğin belirli bir metriği hareket ettireceğini önermek için doğrudan atlamazsınız.

Önerilen değişikliğin ilgili metriği hiçbir şekilde etkilemeyeceğini, bunların alakasız olduğunu söyleyerek başlayın.

Bu sizin boş hipotezinizdir (H0). H0 her zaman değişiklik olmadığıdır. Varsayılan olarak inandığınız şey budur… ta ki denemeniz aksini ispatlayana kadar (ve eğer).

Ve alternatif hipoteziniz (Ha veya H1), olumlu bir değişiklik olduğu yönünde. H0 ve Ha her zaman matematiksel zıtlardır. Ha, önerilen değişikliğin bir fark yaratmasını beklediğiniz yerdir, bu sizin alternatif hipotezinizdir - ve bu, deneyiniz ile test ettiğiniz şeydir.

Bu nedenle, örneğin, fiyatlandırma sayfanızda bir deneme yapmak ve buna başka bir ödeme yöntemi eklemek isteseniz, önce boş bir hipotez oluşturur ve şöyle der: Ek ödeme yönteminin satışlar üzerinde hiçbir etkisi olmayacaktır. Alternatif hipoteziniz şöyle olurdu: Ek ödeme yöntemi satışları ARTIRACAKTIR.

Bir deney yürütmek, aslında, sıfır hipotezine veya statükoya meydan okumaktır.

Tip I ve tip II hatalar, boş hipotezi hatalı olarak reddettiğinizde veya reddetmediğinizde meydana gelir.

Tip I Hatalarını Anlama

Tip I hatalar, yanlış pozitifler veya Alfa hataları olarak bilinir.

Hipotez testinin birinci tip hata örneğinde, optimizasyon testiniz veya deneyiniz * BAŞARILI GÖRÜNÜYOR* ve siz (yanlışlıkla) test ettiğiniz varyasyonun orijinalinden farklı (daha iyi veya daha kötü) yaptığı sonucuna varırsınız.

Tip I hatalarında, yalnızca geçici olan ve uzun vadede devam etmeyecek artışlar veya düşüşler görürsünüz ve sonunda boş hipotezinizi reddedersiniz (ve alternatif hipotezinizi kabul edersiniz).

Sıfır hipotezini hatalı bir şekilde reddetmek çeşitli nedenlerle olabilir, ancak bunların başında göz atma uygulaması gelir (yani, sonuçlarınıza ara dönemde veya deney devam ederken bakmak). Ve testleri, belirlenen durdurma kriterlerine ulaşıldığından daha erken çağırmak.

Birçok test metodolojisi, ara sonuçlara bakmak yanlış sonuçlara yol açarak tip I hatalara yol açabileceğinden, gözetleme uygulamasını caydırır.

Tip I hatasını şu şekilde yapabilirsiniz:

B2B web sitenizin açılış sayfasını optimize ettiğinizi ve buna rozetler veya ödüller eklemenin potansiyel müşterilerinizin kaygısını azaltacağını ve böylece form doldurma oranınızı artıracağını varsaydığınızı varsayalım (daha fazla potansiyel müşteriyle sonuçlanır).

Dolayısıyla, bu deney için boş hipoteziniz şöyle olur: Rozet eklemenin form doldurma üzerinde hiçbir etkisi yoktur.

Böyle bir deney için durdurma kriteri genellikle belirli bir dönemdir ve/veya ayarlanan istatistiksel anlamlılık düzeyinde X dönüşüm gerçekleştikten sonradır. Geleneksel olarak, optimize ediciler %95 istatistiksel güven işaretine ulaşmaya çalışırlar çünkü bu size çoğu optimizasyon deneyi için yeterince düşük kabul edilen tip I hatayı yapma konusunda %5 şans bırakır. Genel olarak, bu metrik ne kadar yüksekse, tip I hata yapma şansı o kadar düşük olur.

Hedeflediğiniz güven düzeyi, tip I hata (α) alma olasılığınızın ne olacağını belirler.

Dolayısıyla, %95'lik bir güven düzeyi hedefliyorsanız, α değeriniz %5 olur. Burada, sonucunuzun yanlış olma ihtimalinin %5 olduğunu kabul ediyorsunuz.

Buna karşılık, denemenizde %99 güven düzeyi ile giderseniz, I. tip hata alma olasılığınız %1'e düşer.

Diyelim ki, bu deney için çok sabırsızsınız ve denemenizin bitmesini beklemek yerine, test aracınızın kontrol paneline (göz atın!) sadece bir gün içinde baktınız. Ve "görünür" bir artış fark ettiniz - form doldurma oranınız %95'lik bir güvenle %29,2 gibi büyük bir artış gösterdi.

Ve BAM…

… deneyini durdurursunuz.

… sıfır hipotezini reddedin (rozetlerin satışlar üzerinde hiçbir etkisi olmadığı).

… alternatif hipotezi kabul edin (rozetlerin satışları artırdığı).

… ve ödül rozetleri olan sürümle çalıştırın.

Ancak, ay boyunca olası satışlarınızı ölçtüğünüzde, sayının orijinal sürümle bildirdiğinizle neredeyse karşılaştırılabilir olduğunu görürsünüz. Sonuçta rozetler o kadar da önemli değildi. Ve boş hipotez muhtemelen boşuna reddedildi.

Burada olan şey, deneyinizi çok erken sonlandırmanız ve sıfır hipotezini reddetmeniz ve yanlış bir kazananla sonuçlanmanızdır - tip I hata yaparsınız.

Deneylerinizde Tip I Hatalardan Kaçınma

Birinci tip hata yapma şansınızı azaltmanın kesin yollarından biri, daha yüksek bir güven düzeyine sahip olmaktır. %5 istatistiksel anlamlılık düzeyi (%95 istatistiksel güven düzeyine çevrilerek) kabul edilebilir. Bu, çoğu optimize edicinin güvenle yapacağı bir bahis çünkü burada, olası olmayan %5 aralığında başarısız olacaksınız.

Yüksek bir güven düzeyi belirlemeye ek olarak, testlerinizi yeterince uzun süre çalıştırmak önemlidir. Test süresi hesaplayıcıları, testinizi ne kadar süreyle çalıştırmanız gerektiğini size söyleyebilir (diğerlerinin yanı sıra belirli bir etki boyutu gibi şeyleri hesaba kattıktan sonra). Bir denemenin amaçlanan seyrini yürütmesine izin verirseniz, 1. tip hatayla karşılaşma şansınızı önemli ölçüde azaltırsınız (yüksek bir güven düzeyi kullanıyorsanız). İstatistiksel olarak anlamlı sonuçlara ulaşana kadar beklemek, sıfır hipotezini hatalı olarak reddetme ve tip I hata yapma olasılığının düşük (genellikle %5) olmasını sağlar. Başka bir deyişle, istatistiksel olarak anlamlı sonuçlar elde etmek için çok önemli olduğundan, iyi bir örnek boyutu kullanın.

Şimdi tüm bunlar, deneylerinizdeki güven (veya önem) düzeyiyle ilgili tip I hatalarla ilgiliydi. Ancak testlerinize sızabilecek başka bir hata türü daha var - tip II hatalar.

Tip II Hataları Anlama

Tip II hatalar, yanlış negatifler veya Beta hataları olarak bilinir.

Tip I hatanın aksine, bir tip II hata durumunda, deney *BAŞARISIZ (VEYA SONUCUNUZ) GÖRÜNÜYOR* ve siz (hatalı bir şekilde) test ettiğiniz varyasyonun, orijinal.

Tip II hatalarda, gerçek artışları veya düşüşleri göremez ve sonuç olarak sıfır hipotezini ve alternatif hipotezi reddetmiş olursunuz.

Tip II hatasını şu şekilde yapabilirsiniz:

Yukarıdan aynı B2B web sitesine geri dönmek…

Bu sefer, formunuzun en üstüne belirgin bir şekilde bir GDPR uyumluluğu sorumluluk reddi beyanı eklemenin, daha fazla müşteri adayını bu formu doldurmaya teşvik edeceğini varsaydığınızı varsayalım (bu, daha fazla olası satışla sonuçlanır).

Bu nedenle, bu deney için boş hipoteziniz şöyle olur: GDPR uyumluluğu sorumluluk reddi beyanı, form doldurmalarını etkilemez.

Ve aynısı için alternatif hipotez şöyledir: GDPR uyumluluğu sorumluluk reddi beyanı, daha fazla form doldurma ile sonuçlanır.

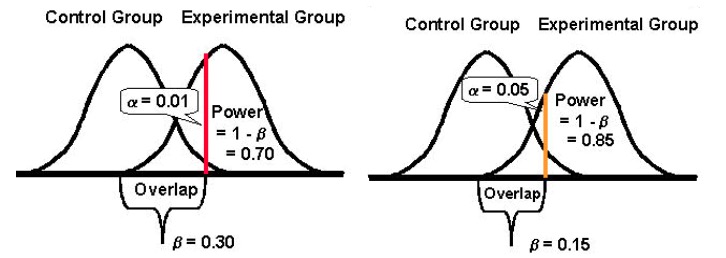
Bir testin istatistiksel gücü, herhangi bir sapma olması durumunda, orijinal ve rakip sürümlerinizin performansındaki farklılıkları ne kadar iyi tespit edebileceğini belirler. Geleneksel olarak, optimize ediciler %80 istatistiksel güç işaretine ulaşmaya çalışırlar çünkü bu ölçüm ne kadar yüksek olursa, II. tip hata yapma şansı o kadar düşük olur.

İstatistiksel güç 0 ile 1 arasında bir değer alır (ve genellikle % olarak ifade edilir) ve tip II hatanızın (β) olasılığını kontrol eder; şu şekilde hesaplanır: 1 – β

Testinizin istatistiksel gücü ne kadar yüksek olursa, II. tip hatalarla karşılaşma olasılığınız o kadar düşük olacaktır.

Dolayısıyla, bir deneyin istatistiksel gücü %10 ise, II. tip hataya oldukça açık olabilir. Oysa bir deneyin istatistiksel gücü %80 ise, II. tip hata yapma olasılığı çok daha düşük olacaktır.

Yine, testinizi yaparsınız, ancak bu sefer form doldurmalarınızda önemli bir artış fark etmezsiniz. Her iki sürüm de benzer dönüşümlere yakın rapor veriyor. Bu nedenle, denemenizi durdurur ve GDPR uyumluluğu sorumluluk reddi beyanı olmadan orijinal sürümle devam edersiniz.

Bununla birlikte, deneme dönemindeki potansiyel müşteri verilerinize daha derine indikçe, her iki sürümdeki (orijinal ve meydan okuyan) potansiyel müşteri sayısı aynı görünse de, GDPR sürümünün size sayı açısından iyi ve önemli bir artış sağladığını görüyorsunuz. Avrupa'dan gelen ipuçları. (Elbette, deneyi yalnızca Avrupa'dan gelen potansiyel müşterilere göstermek için hedef kitle hedeflemeyi kullanabilirdiniz - ama bu başka bir hikaye.)

Burada olan şey, yeterli güce ulaşıp ulaşmadığınızı kontrol etmeden testinizi çok erken bitirmenizdi – II. tip bir hata yaptınız.

Deneylerinizde Tip II Hatalardan Kaçınmak

Tip II hatalardan kaçınmak için yüksek istatistiksel güce sahip testler yapın. Deneylerinizi, en az %80 istatistiksel güç işaretine ulaşabilecek şekilde yapılandırmaya çalışın. Bu, çoğu optimizasyon deneyi için kabul edilebilir bir istatistiksel güç düzeyidir. Bununla, vakaların %80'inde en azından yanlış bir sıfır hipotezini doğru bir şekilde reddedeceğinizden emin olabilirsiniz.

Bunu yapmak için, ona ekleyen faktörlere bakmanız gerekir.

Bunların en büyüğü örneklem büyüklüğüdür (gözlenen bir etki büyüklüğü göz önüne alındığında). Numune boyutu, doğrudan bir testin gücüne bağlıdır. Büyük bir numune boyutu, yüksek güç testi anlamına gelir. Yetersiz testler, özellikle düşük MEI'ler için, meydan okuyucunuz ve orijinal sürümlerinizin sonuçlarındaki farklılıkları tespit etme şansınız büyük ölçüde azaldığından, tip II hatalara karşı çok savunmasızdır (daha fazlası aşağıdadır). Bu nedenle, tip II hatalardan kaçınmak için, tip II hataları en aza indirmek için testin yeterli güç toplamasını bekleyin. İdeal olarak, çoğu durumda en az %80'lik bir güce ulaşmak istersiniz.

Diğer bir faktör, denemeniz için hedeflediğiniz Minimum İlgi Etkisi (MEI) . MEI (MDE olarak da bilinir), söz konusu KPI'nizde tespit etmek istediğiniz minimum fark büyüklüğüdür. Düşük bir MEI ayarlarsanız (örneğin, %1,5'lik bir artış gözlemlerseniz), küçük farkları tespit etmek için önemli ölçüde daha büyük numune boyutları gerektiğinden (yeterli güce ulaşmak için) II. tip hatayla karşılaşma şansınız artar.

Ve son olarak, tip I hata yapma olasılığı (α) ile tip II hata yapma olasılığı (β) arasında ters bir ilişki olma eğiliminde olduğunu belirtmek önemlidir. Örneğin, I. tip hata yapma olasılığını azaltmak için α değerini düşürürseniz (diyelim ki α'yı %1 olarak ayarladınız, bu da %99'luk bir güven düzeyi anlamına gelir), denemenizin istatistiksel gücü (veya yeteneği, β) , var olduğunda bir fark tespit etme) da azalır, böylece II. tip hata alma olasılığınızı artırır.

Hatalardan Herhangi Birini Daha Fazla Kabullenmek: Tip I ve II (& Dengeyi Kurmak)

Bir hata türünün olasılığını düşürmek, diğer türün olasılığını artırır (verilen her şey aynı kalırsa).

Bu nedenle, hangi hata türüne karşı daha toleranslı olabileceğiniz konusunda arama yapmanız gerekir.

Bir yandan tip I hatası yapmak ve bir değişikliği tüm kullanıcılarınız için kullanıma sunmak, size dönüşümlere ve gelire mal olabilir - daha da kötüsü, dönüşüm katili de olabilir.

Öte yandan, II. tip bir hata yapmak ve kazanan bir sürümü tüm kullanıcılarınız için kullanıma sunmamak, başka türlü kazanabileceğiniz dönüşümlere tekrar mal olabilir.

Değişmez bir şekilde, her iki hata da bir maliyetle gelir.

Ancak, denemenize bağlı olarak, biri sizin için diğerine göre daha kabul edilebilir olabilir. Genel olarak, testçiler tip I hatayı tip II hatadan yaklaşık dört kat daha ciddi bulurlar.

Daha dengeli bir yaklaşım benimsemek istiyorsanız, istatistikçi Jacob Cohen, “ alfa ve beta riski arasında makul bir denge” ile gelen %80'lik bir istatistiksel güce gitmenizi önerir. ” (%80 güç aynı zamanda çoğu test aracı için standarttır.)

Ve istatistiksel anlamlılık söz konusu olduğunda, standart %95 olarak belirlenmiştir.

Temel olarak, her şey uzlaşma ve tahammül etmeye hazır olduğunuz risk seviyesi ile ilgilidir. Her iki hata olasılığını da gerçekten en aza indirmek istiyorsanız, %99'luk bir güven düzeyi ve %99'luk bir güç elde edebilirsiniz. Ancak bu, sonsuza kadar uzun görünen süreler için inanılmaz derecede büyük numune boyutlarıyla çalışacağınız anlamına gelir. Ayrıca, o zaman bile hatalar için bir miktar alan bırakmış olursunuz.

Arada bir, bir deneyi yanlış sonuçlandıracaksınız. Ancak bu, test sürecinin bir parçasıdır - A/B testi istatistiklerinde uzmanlaşmak biraz zaman alır. Başarılı veya başarısız deneylerinizi araştırmak ve yeniden test etmek veya takip etmek, bulgularınızı yeniden doğrulamanın veya bir hata yaptığınızı keşfetmenin bir yoludur.