Python'da Tek Nöron Sinir Ağı – Matematiksel Sezgiyle

Tek bir katmanla basit bir ağ oluşturalım - çok çok basit ama eksiksiz bir ağ. Yalnızca bir girdi ve bir nöron (bu da çıktıdır), bir ağırlık, bir önyargı.

Önce kodu çalıştıralım ve sonra parça parça analiz edelim

Github projesini klonlayın veya aşağıdaki kodu favori IDE'nizde çalıştırın.

Bir IDE kurma konusunda yardıma ihtiyacınız varsa, işlemi burada anlattım.

Her şey yolunda giderse, şu çıktıyı alacaksınız:

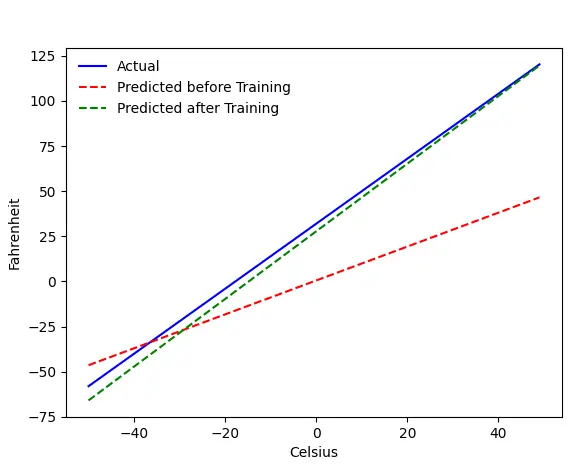
Problem — Celsius'tan Fahrenheit

Makinemizi Celsius'tan Fahrenheit'i tahmin etmesi için eğiteceğiz. Koddan (veya grafikten) anlayabileceğiniz gibi, mavi çizgi gerçek Celsius-Fahrenheit ilişkisidir. Kırmızı çizgi, bebek makinemizin herhangi bir eğitim almadan tahmin ettiği ilişkidir. Son olarak, makineyi eğitiyoruz ve yeşil çizgi, eğitimden sonraki tahmindir.

Satır#65–67'ye bakın - eğitimden önce ve sonra, aynı işlevi kullanarak tahmin yapıyor ( get_predicted_fahrenheit_values() ). Peki sihirli tren () ne yapıyor? Hadi bulalım.

Ağ yapısı

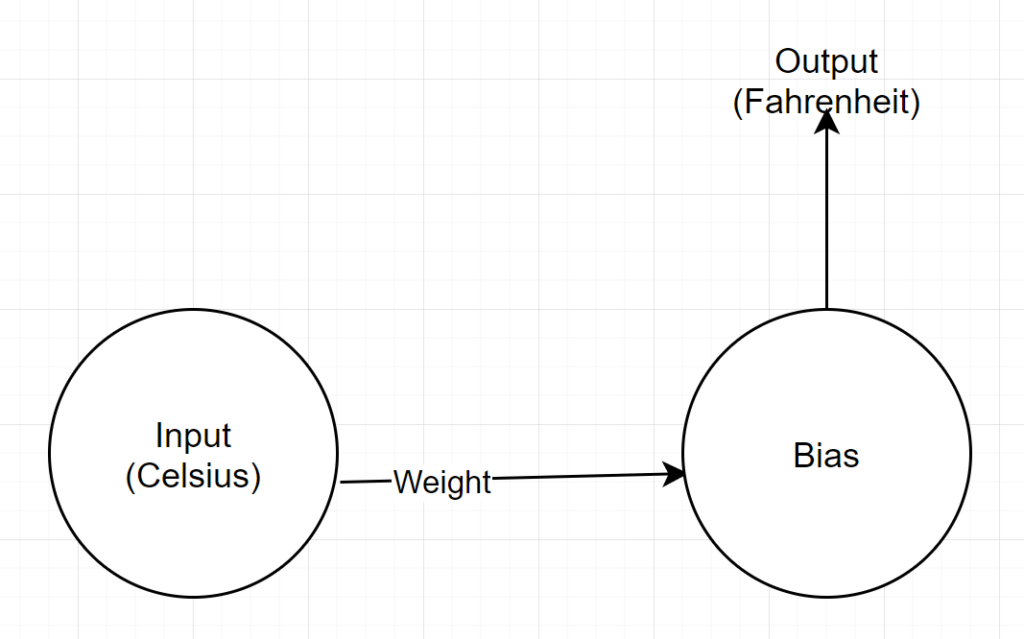
Girdi: Santigratı temsil eden bir sayı

Ağırlık: Ağırlığı temsil eden bir şamandıra

Bias: Önyargıyı temsil eden bir şamandıra

Çıktı: Tahmini Fahrenheit'i temsil eden bir şamandıra

Yani toplam 2 parametremiz var - 1 ağırlık ve 1 önyargı

Kod Analizi

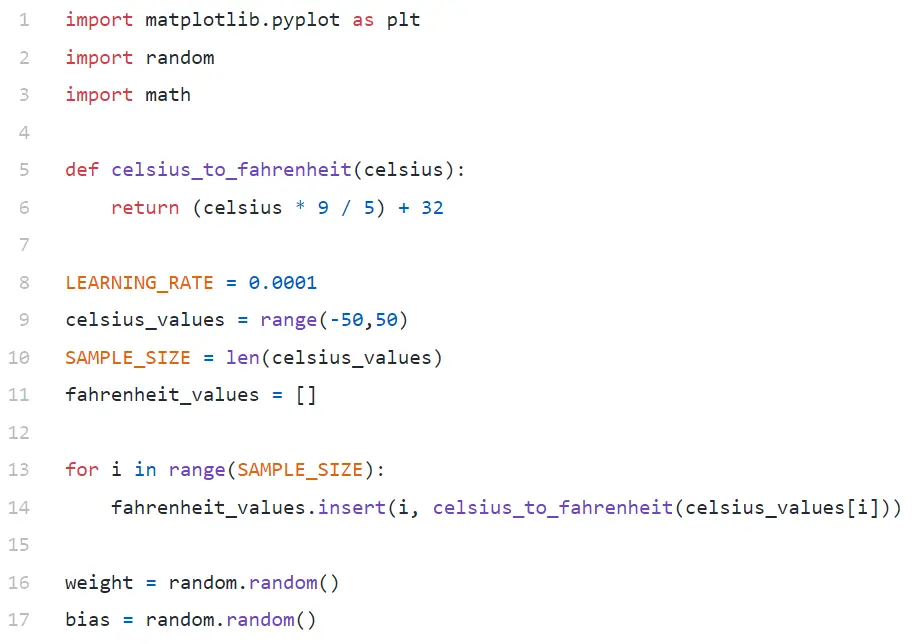
Satır#9'da, -50 ile +50 arasında 100 sayıdan oluşan bir dizi oluşturuyoruz (50 hariç — aralık işlevi üst sınır değerini hariç tutar).

Satır#11–14'te, her santigrat değeri için Fahrenhayt'ı üretiyoruz.

16. ve 17. satırda, ağırlık ve yanlılığı başlatıyoruz.

tren()

Burada 10000 yinelemeli eğitim yürütüyoruz. Her yineleme şunlardan oluşur:

1. ileri (Hat#57) geçişi
2. geriye doğru (Satır#58) geçiş
3. update_parameters (Satır#59)

Python'da yeniyseniz, size biraz garip gelebilir - python işlevleri tuple olarak birden çok değer döndürebilir.

İlgilendiğimiz tek şeyin update_parameters olduğuna dikkat edin. Burada yaptığımız diğer her şey, bu fonksiyonun parametrelerini, yani ağırlık ve sapmamızın gradyanları (aşağıda gradyanların ne olduğunu açıklayacağız) değerlendirmektir.

1. grad_weight: Ağırlık gradyanını temsil eden bir şamandıra
2. grad_bias: Önyargı gradyanını temsil eden bir şamandıra

Bu değerleri geriye doğru çağırarak elde ederiz, ancak 57. satırda ileriye doğru çağırarak elde ettiğimiz çıktıyı gerektirir.

ileri()

Burada celsius_values ​​ve fahrenheit_values ​​değerlerinin 100 satırlık diziler olduğuna dikkat edin:

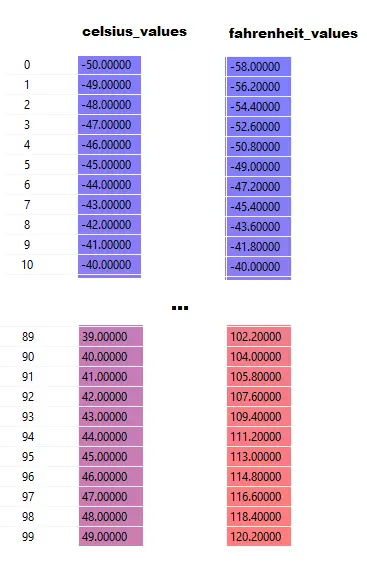
Satır#20–23'ü çalıştırdıktan sonra, santigrat değeri için 42 deyin.

çıktı = 42 * ağırlık + önyargı

Bu nedenle, celsius_values ​​içindeki 100 öğe için çıktı, karşılık gelen her bir santigrat değeri için 100 öğelik bir dizi olacaktır.

Satır#25–30, tüm farkların karesinin örnek sayısına bölünmesinin (bu durumda 100) süslü bir adı olan Ortalama Kare Hatası (MSE) kayıp işlevini kullanarak kaybı hesaplamaktadır.

Küçük kayıp, daha iyi tahmin anlamına gelir. Her yinelemede yazdırma kaybını devam ettirirseniz, eğitim ilerledikçe azaldığını göreceksiniz.

Son olarak, Satır#31'de tahmin edilen çıktı ve kaybı döndürüyoruz.

geriye

Sadece ağırlığımızı ve önyargımızı güncellemekle ilgileniyoruz. Bu değerleri güncellemek için gradyanlarını bilmeliyiz ve burada hesapladığımız şey bu.

Dikkat gradyanları ters sırada hesaplanmaktadır. Önce çıktının gradyanı, ardından ağırlık ve sapma için hesaplanır ve bu nedenle “geri yayılım” adı verilir. Bunun nedeni, ağırlık ve sapma gradyanını hesaplamak için çıktı gradyanını bilmemiz gerekiyor - böylece onu zincir kuralı formülünde kullanabiliriz.

Şimdi degrade ve zincir kuralının ne olduğuna bir göz atalım.

Gradyan

Basitlik adına, sırasıyla 42 ve 107.6 celsius_values ​​ve fahrenheit_values ​​değerlerinden yalnızca bir tanesine sahip olduğumuzu düşünün.

Şimdi, Satır#30'daki hesaplamanın dökümü şöyle olur:

kayıp = (107.6 — (42 * ağırlık + sapma))² / 1

Gördüğünüz gibi, kayıp 2 parametreye bağlıdır - ağırlıklar ve önyargı. Ağırlığı düşünün. Diyelim ki 0.8 gibi rastgele bir değerle başlattık ve yukarıdaki denklemi değerlendirdikten sonra kayıp değeri olarak 123.45 elde ettik. Bu kayıp değerine göre kilonuzu nasıl güncelleyeceğinize karar vermelisiniz. 0.9 mu yoksa 0.7 mi yapmalısın?

Ağırlığı bir sonraki yinelemede kayıp için daha düşük bir değer elde edecek şekilde güncellemeniz gerekir (unutmayın, kaybı en aza indirmek nihai hedeftir). Yani kiloyu artırmak kaybı arttırırsa, onu azaltacağız. Ve kiloyu arttırmak kaybı azaltırsa, onu arttırırız.

Şimdi soru, ağırlıkların artmasının kaybı artıracağını veya azaltacağını nasıl bileceğiz. Gradyanın geldiği yer burasıdır . Genel olarak, gradyan türev ile tanımlanır. Lise hesaplarınızdan hatırlayın, ∂y/∂x (y'nin x'e göre kısmi türevi/gradyanıdır), x'teki küçük bir değişiklikle y'nin nasıl değişeceğini gösterir.

∂y/∂x pozitifse, x'teki küçük bir artışın y'yi artıracağı anlamına gelir.

∂y/∂x negatifse, bu, x'teki küçük bir artışın y'yi azaltacağı anlamına gelir.

∂y/∂x büyükse, x'teki küçük bir değişiklik y'de büyük bir değişikliğe neden olur.

∂y/∂x küçükse, x'teki küçük bir değişiklik y'de küçük bir değişikliğe neden olur.

Böylece, gradyanlardan 2 bilgi alırız. Parametrenin hangi yönde (artış veya azalış) ve ne kadar (büyük veya küçük) güncellenmesi gerektiği.

Zincir kuralı

Gayri resmi olarak konuşursak, zincir kuralı şöyle der:

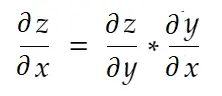
Yukarıdaki ağırlık örneğini düşünün. Bu ağırlığı güncellemek için derece_ağırlığını hesaplamamız gerekiyor, bu da şu şekilde hesaplanacak:

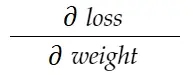
Zincir kuralı formülü ile şunu türetebiliriz:

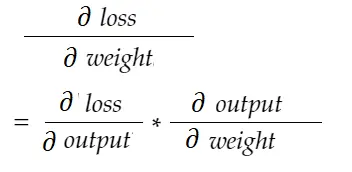
Benzer şekilde, önyargı için gradyan:

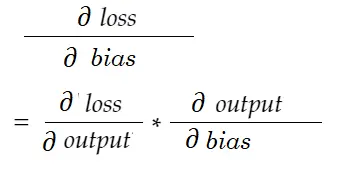
Bir bağımlılık diyagramı çizelim.

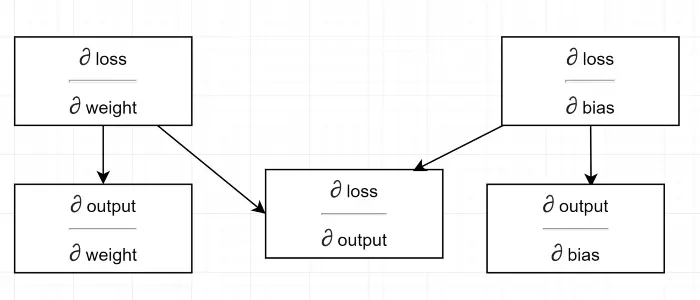
Tüm hesaplamaların çıktının derecesine bağlı olduğunu görün (∂ kayıp/∂ çıktı) . Bu yüzden ilk olarak geri geçişte hesaplıyoruz (Hat#34–36).

Aslında, yüksek seviyeli ML çerçevelerinde, örneğin PyTorch'ta, geri geçiş için kod yazmanız gerekmez! İleri geçiş sırasında hesaplamalı grafikler oluşturur ve geri geçiş sırasında grafikte zıt yönlerden geçerek gradyanları zincir kuralı kullanarak hesaplar.

∂ kayıp / ∂ çıktı

Bu değişkeni Satır#34–36'da hesapladığımız kodda grad_output ile tanımlarız. Kodda kullandığımız formülün nedenini bulalım.

Unutmayın, makinedeki 100 santigrat derecenin hepsini birlikte besliyoruz. Dolayısıyla, grad_output 100 öğeden oluşan bir dizi olacaktır, her öğe celsius_values ​​içinde karşılık gelen öğe için çıktı gradyanını içerir. Basitlik için, celsius_values ​​içinde sadece 2 öğe olduğunu düşünelim.

30 numaralı satırı kırmak,

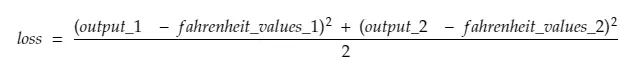
nerede,

output_1 = 1. santigrat değeri için çıkış değeri

output_2 = 2. santigrat değeri için çıkış değeri

fahreinheit_values_1 = 1. santigrat değeri için gerçek fahreinhayt değeri

fahreinheit_values_1 = 2. santigrat değeri için gerçek fahreinhayt değeri

Şimdi, elde edilen grad_output değişkeni 2 değer içerecektir - output_1 ve output_2 gradyanı, yani:

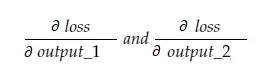
Sadece output_1 gradyanını hesaplayalım ve sonra aynı kuralı diğerleri için de uygulayabiliriz.

Hesap zamanı!

Bu, #34-36 numaralı satırla aynıdır.

Ağırlık gradyanı

Düşünün, celsius_values ​​içinde yalnızca bir öğemiz var. Şimdi:

Bu, Satır#38-40 ile aynıdır. 100 santigrat derece için, değerlerin her biri için gradyan değerleri toplanacaktır. Açık bir soru, sonucu neden küçültmüyoruz (yani SAMPLE_SIZE ile bölmek) olacaktır. Parametreleri güncellemeden önce tüm gradyanları küçük bir faktörle çarptığımız için gerekli değildir (bkz. son bölüm Parametreleri Güncelleme).

önyargı gradyanı

Hangi Satır # 42 ile aynıdır. Ağırlık gradyanları gibi, 100 girdinin her biri için bu değerler toplanıyor. Parametreleri güncellemeden önce gradyanlar küçük bir faktörle çarpıldığı için yine sorun yok.

Parametrelerin Güncellenmesi

Son olarak, parametreleri güncelliyoruz. Eğitimi kararlı hale getirmek için çıkarılmadan önce gradyanların küçük bir faktörle (LEARNING_RATE) çarpıldığına dikkat edin. LEARNING_RATE'in büyük bir değeri, bir aşma sorununa neden olur ve çok küçük bir değer, eğitimi yavaşlatır ve bu da çok daha fazla yineleme gerektirebilir. Biraz deneme yanılma ile bunun için en uygun değeri bulmalıyız. Öğrenme Hızı hakkında daha fazla bilgi edinmek için bu da dahil olmak üzere birçok çevrimiçi kaynak var.

Dikkat edin, ayarladığımız tam miktar son derece kritik değil. Örneğin, LEARNING_RATE'i biraz ayarlarsanız, iniş_grad_ağırlığı ve descent_grad_bias değişkenleri (Satır#49–50) değiştirilir, ancak makine çalışmaya devam edebilir. Önemli olan, aynı faktörle (bu durumda LEARNING_RATE) gradyanları küçülterek bu miktarların elde edilmesini sağlamaktır. Başka bir deyişle, “gradyanların inişini orantılı tutmak”, “ne kadar indiklerinden ” daha önemlidir.

Ayrıca, bu gradyan değerlerinin aslında 100 girişin her biri için değerlendirilen gradyanların toplamı olduğuna dikkat edin. Ancak bunlar aynı değerde ölçeklendirildiği için yukarıda belirtildiği gibi iyidir.

Parametreleri güncellemek için bunları global anahtar kelime ile (Satır#47'de) bildirmeliyiz.

Buradan nereye gidilir

For döngülerini Pythonic şekilde liste anlama ile değiştirerek kod çok daha küçük olacaktır. Şimdi bir göz atın - anlamak birkaç dakikadan fazla sürmez.

Şimdiye kadar her şeyi anladıysanız, muhtemelen birden fazla nöron/katman içeren basit bir ağın iç kısımlarını görmenin tam zamanıdır - işte bir makale.