Normal Dağılım – Matematiksiz Sezgisel Bir Giriş

Bu makaleyi mümkün olduğunca denklemlerden ve ağız dolusu jargonlardan uzak tutmaya çalışacağım. Ancak, en azından aşağıdaki yeteneklere sahip olmanızı istiyorum:

• Basit grafikleri yorumlayabilir.
• Olasılıkla ilgili temel düzeyde bilgi. Yazı-tura atarsam en azından tura gelme olasılığının %50 olduğunu anlamışsınızdır.
• İntegral hesap ve kuantum fiziği (şaka!)

Neden Normal Dağılım

Bir şeyi anlamanın sezgisel bir yolu, neden gerekli olduğunu araştırmaktır. Bunu normal dağılım için yapalım (Gauss Dağılımı da denir).

Komik bir alışkanlığın olduğunu söyle. Her gün 100 defa yazı tura atıyorsunuz. Günün çoğunda 50 kez veya 50'ye yakın bir zamanda başınızın dönmesini beklemek “normaldir”. Nadiren, kafa için iyi günler vardır - yaklaşık 55 kat ve çok nadiren 65 katın üzerine çıkabilirsiniz.

Şimdi, bu “nadirliği” ölçmek istiyorsunuz. Böylece her gün kaç kez kafayı yediğinizi takip etmeye başlarsınız.

Bir yılda her gün kafa sayısı

Aşağıda bir yıl (365 gün) sonraki veriler verilmiştir - ilki ilk gün aldığınız tura sayısı, sonuncusu ise son gün aldığınız tura sayısıdır. Aşağıdaki tüm sayıları kontrol etmenize gerek yok, ancak çoğunun 50 civarında olduğunu anlamak kolaydır.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Histogram ile Daha İyi Görselleştirin

Yukarıdaki verilerden bir histogram çizelim:

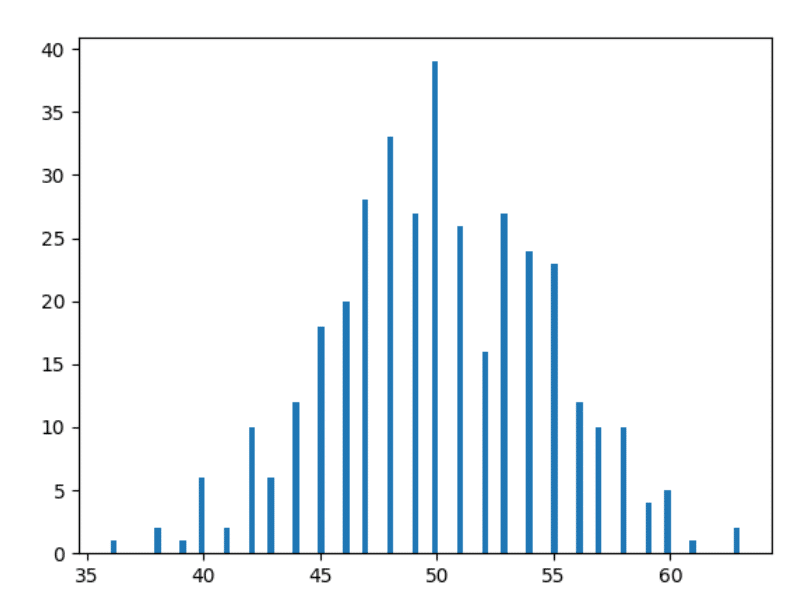
Aha! İnternette “Normal Dağılım” arattığınızda gördüğünüz görüntü zaten böyle değil mi? Neredeyse geldik!

Bu nedenle, eğer histogramları anlamıyorsanız – burada belirli bir kafa sayımı aldığımız günlerin sayısını belirledik. Örneğin, yılın belirli 2 gününde 36 kez kafa aldık (bana inanmıyorsanız yukarıdaki verilere bakın), bu yüzden 36'daki yatay noktada 2 birim yüksekliğinde bir çubuk var (kırmızı Aşağıdaki resimde soldaki dikdörtgen).

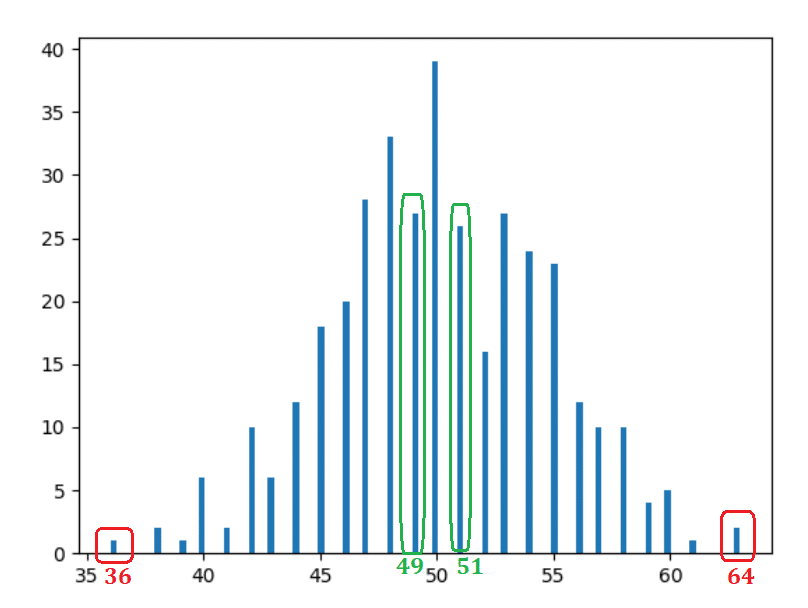
gözlemler

1. Oldukça açık ve beklenen - çoğu zaman 50 kafa meydana geldi.
2. Merkezden (50) uzaklaştıkça görülme sıklığı azalmaktadır.
3. Aynı mesafedeki çubuklar benzer şekiller alır. Örneğin, bir birimi sola (49) veya sağa (51) hareket ettirirseniz — oluşumlar benzerdir — sırasıyla 30 ve 31 (yeşil dikdörtgenler). 14 birim sola (36) veya sağa (64) hareket ettirirseniz, oluşumlar yine benzerdir - sırasıyla 2 ve 1 (kırmızı dikdörtgenler).

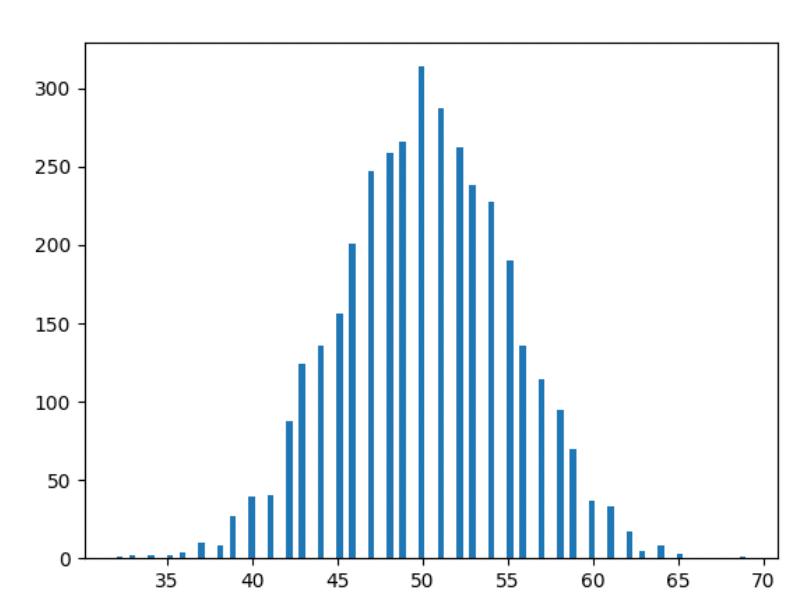
10 yıllık veriler

Şimdi biraz ileri saralım ve 10 yıllık verileri çizelim.

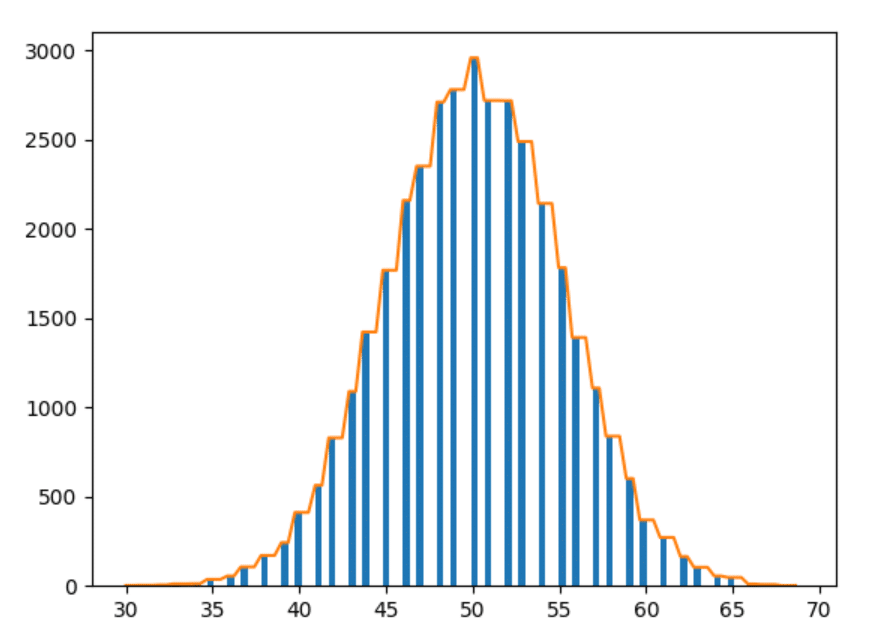
1000 yıllık veriler

Tamam - sonuncusu. 1000 yıllık verileri çizelim.

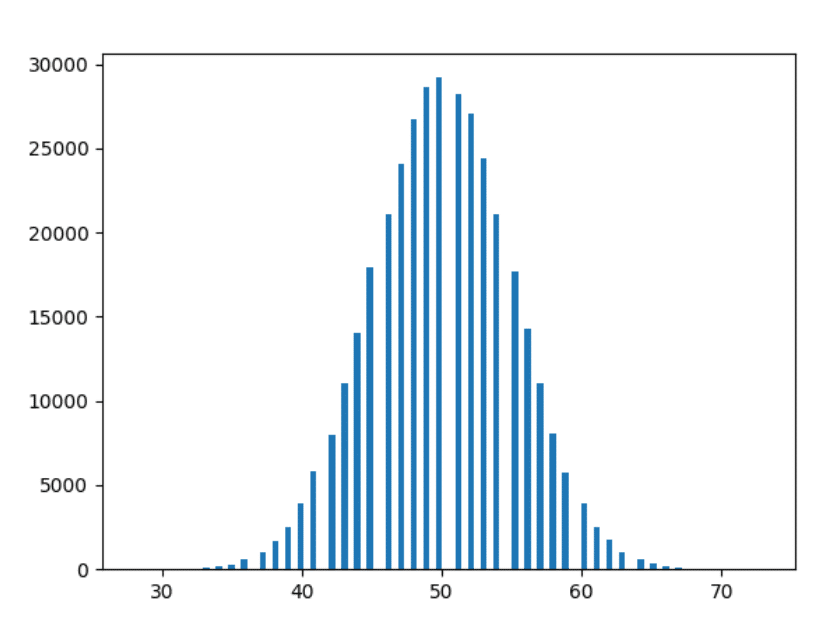
gözlemler

1. Ne kadar çok deney yaparsak, şekiller o kadar düzgün olur.
2. Ne kadar çok deney yaparsak, çubuklar yukarıdaki gözlemleri o kadar çok takip eder (yani, benzer mesafedeki çubuklar daha yakın şekiller alır).

Lanet olası normal dağılım nerede?

Tamam - çok fazla arka plan - şimdi konuya gelelim.

Google'ın önerdiği cevaba bakalım:

Bu tanımdaki birkaç şey:

Rastgele Değişken: Basitçe söylemek gerekirse - rastgele bir değişken, yazı tura gibi rastgele bir deneyin olası değerleri kümesidir. Örneğimizde, deneyimizin olası değeri Baş veya Kuyruktur .

Çan Şeklinde: Histogramımızın çan şeklini aldığını fark ettiniz mi?

Simetrik: Aynı mesafedeki çubuklar benzer şekillere sahiptir - simetrik değil mi?

Bu nedenle, normal dağılım, simetri ve çan şekli dahil olmak üzere dağılımın birkaç özelliği koruma eğiliminde olduğu yazı tura gibi olaylar için sonuçların dağılımını temsil eder.

Yazı tura dışında hangi fenomenler normal dağılımı takip eder?

Burada bazı harika örnekler.

• Nüfustaki yükseklik - daha fazla insan ortalama boy grubuna girer. Aşırı uzun veya aşırı kısa insanlar bulmak nadirdir. Ve son derece uzun ve son derece kısa bulma şansı neredeyse eşittir.
• zar atmak
• Ayakkabı numarası
• IQ
• Ve daha bir çok…

Bu fenomenler kesinlikle normal dağılımı takip ediyor mu?

Basit cevap hayır. Yukarıda gördüğümüz gibi - ne kadar çok deney yaparsanız, veriler o kadar normal dağılım özelliklerini izleyecektir. Ancak olası olmayan bir olayın yine de gerçekleşmeyeceğinin garantisi yoktur.

Evrendeki tüm olasılık dağılımları normal dağılım mıdır?

Hayır. Başka bir tür dağılım tarafından belirlenen birçok fenomen vardır.

• Belirli sayıda müşterinin gelme olasılığı, telefon görüşmeleri, kazalar, spor etkinlikleri ve seller Poisson Distribution'ı takip eder.
• Ticari satışlar için, bir şirketin müşterilerinin %20'si, satışların %80'inden sorumludur. ( Pareto Dağılımı )
• Bir şehirdeki trafik kalıpları — Üstel Dağılım
• Kız ve erkek nüfustan bir takım için rastgele üye seçimi - Hipergeometrik Dağılım

Ve daha fazlası …

Yukarıdaki listeyi, burada listelenen bazı dağıtımlarla "gerçek hayat örneği" aratarak oluşturdum - hepsini anladığımdan değil. 😉

Bazı doğal olayların normal dağılıma uyma eğiliminde olmasının bir nedeni var mı?

Evet - en sevdiğim açıklamayı alıntılayarak:

Genel açıklama, normal dağılım için “hata dağılımı” olan başka bir adla verilir. Buradaki fikir, hataların genellikle rastgele olduğu, böylece bir yöne gitme olasılığı diğer yönde olduğu kadar olasıdır. Örneğin, nişancının biraz sola, biraz sağa veya biraz yükseğe ve biraz aşağıya ateş etmesi muhtemeldir. Böylece, atışların bullseye ne kadar uzak olduğunu gösteren bir grafik bu rastgele eğilimi yansıtacak ve ortalama etrafında simetrik olacaktır. Benzer şekilde, boy ve zeka ile - beslenme, hastalıklar, düşük gelir ve benzeri gibi çok sayıda çevresel faktör gibi birçok gen (belki de binlerce) bu sonuçlara katkıda bulunur.

Normal dağılım parametreleri

Şimdiye kadar tartışmanın bir sezgisine sahipseniz - zaten kazanan sizsiniz. Görev tamamlandı. Makalenin geri kalanı bir bonus.

Gördüğünüz tüm normal dağılım grafikleri şekil olarak farklıdır. Bazıları diğerlerinden daha düzdür. Bazılarının yüksekliği iyi. Tüm bu şekiller sadece 2 parametre ile kontrol edilir:

Anlamına gelmek

Ortalama, ortalama ile tanımlanır. Zilin yüksekliğini tanımlar. Yazı tura örneğinde, ortalama, grafiğin en üst konumu olan 50'ye yakındır.

Standart sapma

Bu makalenin denklemlerden arındırılacağına söz verdiğim için burada matematiksel gösterimini vermiyorum. Ama yine de o kadar zor değil. Standart sapma, verilerin ne kadar çeşitli olduğunu gösteren bir ölçümdür.

Örneğin, çocuk bakımında yaş standart sapması, futbol fan kulübündeki yaşın standart sapmasından daha düşük olacaktır, çünkü futbol fan kulübünde en genç ve en yaşlı grup arasındaki yaş farkı çok daha yüksek olmalıdır.

Standart sapma eğrinin genişliğini belirler. Küçük bir standart sapma dik bir eğri, daha büyük bir standart sapma ise daha düz bir eğri üretir.