Bayes İstatistikleri: Bir A/B Testçisinin Hızlı ve Heyecansız Astarı
Yayınlanan: 2022-06-23
A/B test aracınız tarafından sağlanan sonuçları yorumlama yeteneğinizden ne kadar eminsiniz?
Diyelim ki, Bayes istatistiklerine dayalı bir araç kullanıyorsunuz ve size “B”nin “A”yı geçme şansının %70 olduğunu ve dolayısıyla “B”nin kazanan olduğunu söyledi. Bunun ne anlama geldiğini ve CRO stratejinizi nasıl bilgilendirmesi gerektiğini biliyor musunuz?
Bu makalede, A/B testinizin kontrolünü tekrar ele almanıza yardımcı olacak Bayes istatistiklerinin temellerini öğreneceksiniz.
- Bayes istatistiklerine tarafsız bir bakış
- Frequentist vs Bayesian avantajları ve dezavantajları
- Bazı yaygın efsane tuzaklarından kaçınırken, Bayesian A/B test sonuçlarını güvenle yorumlamak ve kullanmak için ihtiyacınız olan hazırlık.
- Bayes İstatistikleri Nedir?
- Bayes Köken Hikayesi
- A/B Testine Uygulanan Bayes İstatistiklerine Bir Örnek
- A/B Test Kullanıcıları için Önemli Bayes Terimlerinin Kısa Sözlüğü
- Bayes Çıkarımı
- Şartlı olasılık
- Olasılık Dağılımı/Olasılık Dağılımı
- Önceki İnanç Dağılımı
- eşlilik
- konjuge öncelikler
- Kayıp Fonksiyonu
- Sıkça İstatistik nedir?
- Bayesian vs Frequentist A/B Testi
- Sıkça Kullanılan Çerçeve
- Bayes Çerçevesi
- Bayes İstatistikleri A/B Testinde Size Gerçekte Ne Diyor?
- En İyi Olma Olasılığı (P2BB)
- Beklenen Artış
- Beklenen Kayıp
- Bayes İstatistiklerinden Kaçınılması Gereken Mitler
- Efsane 1: Bayesçiler Varsayımlarını Belirtirler, Sıkça Kullananlar Söylemez
- Efsane #2. Bayes Yöntemleri Size Aslında İstediğiniz Cevapları Verir
- Efsane #3: Bayes Çıkarımı, Belirsizliği Sıkça Çıkarımdan Daha İyi Anlatmanıza Yardımcı Oluyor
- Efsane #4. Bayes A/B Testi Sonuçları Göz Atmaya Bağışıklıdır
- Efsane #5. Sabit Bir Örnek Boyutunu Beklemeniz Gerektiğinden Sıkça Kullanılan İstatistikler Verimsizdir
- Peki, Bayesian mı yoksa Frequentist mi Seçmelisiniz? İkisinin de Yeri Vardır.
- Anahtar Paket Servis
Hazır? Temel bilgilerle başlayalım.
Bayes İstatistikleri Nedir?
Bayes istatistikleri, Bayes teoremine dayanan ve olaylarla ilgili inançları yeni veriler veya bu olaylarla ilgili kanıtlar toplanırken güncelleyen istatistiksel analize yönelik bir yaklaşımdır. Burada olasılık, bir olayın meydana geldiğine dair inancın bir ölçüsüdür.
Bunun anlamı: Bir olay hakkında önceden bir inancınız varsa ve onunla ilgili daha fazla bilgi alırsanız, bu inanç sonradan bir inanca dönüşecektir (veya en azından uyarlanacaktır).
Bu, belirsizliği anlamak için veya e-ticaret için dönüşüm oranı optimizasyonu ve makine öğrenimi gibi çok sayıda gürültülü veriyle çalışırken yararlıdır.
Bunu hayal edelim:
Örneğin, bir kolej market arabası yarışını izliyorsunuz ve sonra heyecanlı bir seyirci sizi kırmızı tişörtlü adamın yeşil tişörtlü bayana el atacağı üzerine bir bahse davet ediyor. Bunu düşünün ve bunun yerine siyah ceketli adam ve siyah kapüşonlu kızın kazanacağına karşı çıkıyorsunuz.

Tepede başka bir seyirci ve size bir tüyo fısıldadı, "Kırmızı tişörtlü adam 4 yarıştan son 3'ünü kazandı." Bahsiniz ne olacak? Artık pek emin değilsin, değil mi?
Siyah ceketli adamın uğurlu güneş gözlüklerini en son taktığında kazandığını da öğrendiğinizi varsayalım. Ve giymediği zamanlarda kırmızı tişörtlü adam kazandı.
Bugün siyah ceketli adamın o gözlükleri taktığını görüyorsunuz. İnancın yine değişir. Artık bahsine daha çok inanıyorsun, değil mi? Bu hikayede, her yeni veri kanıtı aldığınızda inancınızı güncellediniz. Bayes yaklaşımı budur.
Bayes Köken Hikayesi
Rahip Thomas Bayes teorisini ilk kez düşündüğünde, bunun yayınlanmaya değer olduğunu düşünmedi. Böylece, on yıldan fazla bir süre notlarında kaldı. Ailesi Richard Price'ın notlarını gözden geçirmesini istediğinde Price, Bayes Teoreminin temelini oluşturan notları keşfetti.
Bayes için bir düşünce deneyi ile başladı. Tamamen düz ve kare bir masaya sırtını vererek oturmayı ve bir yardımcısının masaya bir top atmasını sağlamayı düşündü.
Top masanın herhangi bir yerine düşebilirdi ama Bayes, tahminlerini yeni bilgilerle güncelleyerek nereye gideceğini tahmin edebileceğini düşündü. Top masaya düştüğünde, asistanına, önceki topun düştüğü yerin önüne veya arkasına, sola mı, sağa mı düştüğünü söylemesini isterdi.
Bunu not etti ve masaya daha fazla top düştüğünde dinledi. Bunun gibi ek bilgilerle, her atışta tahminlerinin doğruluğunu artırabileceğini keşfetti. Bu, gözlemden daha fazla kanıt elde ettiğimiz için anlayışımızı güncelleme fikrini getirdi.
Veri analizine Bayes yaklaşımı, bilim ve mühendislik gibi çeşitli alanlarda uygulanır ve hatta spor ve hukuku içerir.
Çevrimiçi rastgele kontrollü deneylerde, özellikle A/B testinde Bayes yaklaşımını 4 adımda kullanabilirsiniz:
- Önceki dağıtımınızı tanımlayın.
- İnançlarınızı yansıtan istatistiksel bir model seçin.
- Deneyi çalıştırın.
- Gözlemden sonra inançlarınızı güncelleyin ve bir sonsal dağılım hesaplayın.
Bayes algoritması adı verilen bir dizi kural kullanarak inançlarınızı güncellersiniz.
A/B Testine Uygulanan Bayes İstatistiklerine Bir Örnek
Bir Bayes A/B testi örneğini açıklayalım.
Bir Shopify mağazasının CTA düğmesi üzerinde basit bir A/B testi yaptığımızı hayal edin. “A” için “Sepete Ekle” ve “B” için “Sepetinize Ekle” kullanıyoruz.
İşte bir frekansçının teste nasıl yaklaşacağı.
İki alternatif dünya vardır: Biri A ve B'nin farklı olmadığı, bu nedenle test, dönüşüm oranında herhangi bir fark göstermeyecektir. Bu boş hipotez. Ve diğer dünyada bir fark var, yani bir düğme diğerinden daha iyi performans gösterecek.
Sık kullanan kişi, CTA düğmelerinde hiçbir farkın olmadığı, yani boş hipotezin doğru olduğunu varsayarak, 1. dünyada yaşadığımızı varsayacaktır. Ve sonra bunun yanlış olduğunu, önem düzeyi adı verilen önceden belirlenmiş bir kesinlik düzeyine kadar kanıtlamaya çalışacaklar.
Ancak bir Bayesian aynı teste şu şekilde yaklaşacaktır:
A ve B düğmelerinin her ikisinin de 0 ile %100 arasında bir dönüşüm oranı üretme şansının eşit olduğuna dair önceden bir inançla başlarlar. Yani, kapıdan hemen sonra düğme eşitliği var - her ikisinin de en iyi performans gösteren olma şansı %50.
Ardından test başlar ve veriler toplanır. Bayesian A/B test kullanıcıları, yeni bilgileri gözlemleyerek bilgilerini güncelleyecektir. Yani, eğer B umut veriyorsa, “B'nin A'yı yenme şansı %61'dir” diyerek bu gözleme dayalı olarak sonradan gelen bir inanca ulaşabilirler.
İki yöntem arasında temel farklılıklar vardır.
Bu nedenle Bayesian A/B testine tarafsız bir yaklaşım benimsememiz önemlidir.
Bayesian A/B test araçlarının çoğu - belki pazarlama amaçları için - aşırı sıklık karşıtı bir duruş sergiler ve Bayesian'ın size hangi varyantın daha "karlı" olduğunu söylemede daha iyi olduğu argümanını zorlar.
Ancak, A/B testine yönelik herhangi bir tek istatistiksel yaklaşım, içgörülerin münhasır haklarına sahip midir?
Bayesci argüman daha da ileri götürülürse, katılımcıların en iyi hareket tarzının ne olduğunu bilmek istediklerini veya karları veya benzer bir şeyi maksimize etmek istediklerini söyledikleri araştırmalarla karşı karşıya kalabilirler. Bu, soruyu kesin olarak karar-teorik alanına sokar - ne Bayes çıkarımının ne de sıklıkçı çıkarımın doğrudan söz sahibi olamayacağı bir şey.
Analytics-toolkit.com'un yaratıcısı ve “Çevrimiçi A/B Testinde İstatistiksel Yöntemler” kitabının yazarı Georgi Georgiev
Önümüzdeki bölümlerde bu ayrıntılara kısa bir dalış yapacağız. Şimdilik, bu astarın geri kalanını kavramayı kolaylaştıralım.
A/B Test Kullanıcıları için Önemli Bayes Terimlerinin Kısa Sözlüğü
Bayes Çıkarımı
Bayes çıkarımı, bir hipotezin olasılığını yeni verilerle güncellemektir. İnançlar ve olasılıklar üzerine inşa edilmiştir.
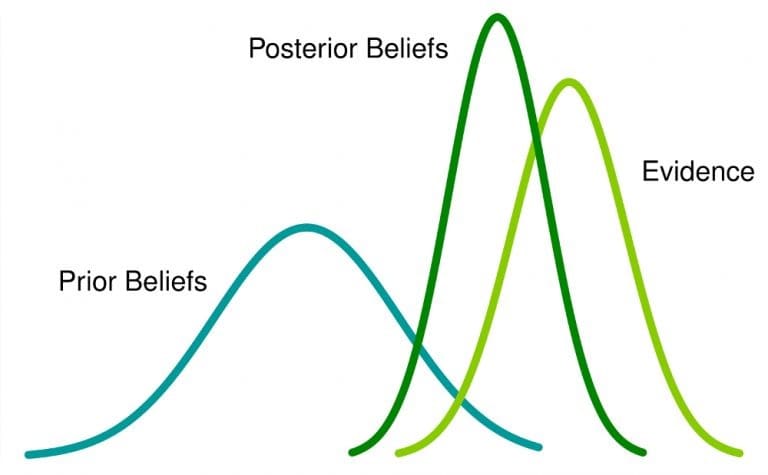
Bayes çıkarımı, verilerin inançlarımızı nasıl etkilediğini anlamamıza yardımcı olmak için koşullu olasılığı kullanır. Diyelim ki gökyüzünün kırmızı olduğuna dair önceden bir inançla başladık. Bazı verilere baktıktan sonra, bu önceki inancın yanlış olduğunu hemen anlayacağız. Bu nedenle, gökyüzünün rengiyle ilgili yanlış modelimizi iyileştirmek için Bayes güncellemesi yapıyoruz ve daha doğru bir arka inanışla sonuçlanıyoruz .
Michael Berk, Veri Bilimine Doğru
Şartlı olasılık
Koşullu olasılık, başka bir olayın meydana geldiği göz önüne alındığında bir olayın olasılığıdır. Yani, B koşulunda A'nın olasılığı.
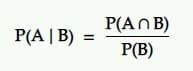
Tercüme: Başka bir B olayı verildiğinde bir A olayının olma olasılığı, B ve A'nın birlikte olma olasılığının B olayının olasılığına bölünmesine eşittir.
Olasılık Dağılımı/Olasılık Dağılımı
Olasılık dağılımları, verilerinizin belirli bir değeri alma olasılığını gösteren dağılımlardır.
Verilerinizin, örneğin gri, kırmızı, turuncu, mavi vb. olabilen renkler gibi bir kategori gibi birden çok değer alabileceği durumlarda, dağılımınız çok terimlidir. Bir dizi sayı için dağılım normal olabilir. Ve evet/hayır veya doğru/yanlış olabilen veri değerleri için binom olur.
Önceki İnanç Dağılımı
Veya basitçe önsel olarak adlandırılan önceki olasılık dağılımı, yeni verilere dair kanıt elde etmeden önceki inancınızı ifade eder. Yani, Bayes analizini (veya çıkarımını) kullanarak bazı kanıtları değerlendirdikten sonra güncelleyeceğiniz ilk inancınızın bir ifadesidir.
eşlilik
Her şeyden önce, eşlenik, genellikle çiftler halinde bir araya gelmeyi ifade eder. Bayesian olasılık teorisinde, eşlenik, öncekinin olabilirliğe eşlenik olduğunu varsaymaktır.
Posterior, önceki ile aynı işlevsel forma sahipse, o zaman önceki, olabilirlik fonksiyonuna eşleniktir. Bu, olabilirlik fonksiyonunun önceki dağılımı nasıl güncellediğini gösterir.
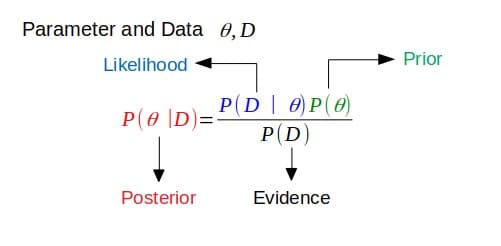
konjuge öncelikler
Bu, yukarıdaki tanımla bağlantılıdır. Sonuncusu, önceki olasılık dağılımıyla aynı olasılık dağılım ailesindeyse (veya aynı işlevsel forma sahipse), önceki ve sonrakiler eşlenik dağılımlardır. Bu durumda, olabilirlik fonksiyonu için önceliğe önceki eşlenik denir.
Sübjektif (deneycinin bilgisine dayanarak), objektif ve bilgilendirici (tarihsel verilere dayalı) veya bilgilendirici olmayabilirler.
Kayıp Fonksiyonu
Kayıp fonksiyonu, mevcut tahminimizin ne kadar kötü olduğunu ölçerek kaybı nicelleştirmenin bir yoludur. Özellikle bir dizi olası değerde yer alan bir çıkarımı ifade ederken, hipotez testi için kaybı en aza indirmemize yardımcı olur ve test sonuçlarımızla karar vermeyi destekler.
Şimdi bu yoldan çıktı, devam edebiliriz.
Bir süredir bloğun etrafındaysanız, muhtemelen birkaç Frequentist ve Bayesian istatistik memesinden daha fazlasıyla karşılaşmışsınızdır.

Her iki taraf da karşıt yönlerden cevaplar arıyor gibi görünüyor, ancak durum gerçekten böyle mi? Bunu daha iyi anlamak için (tarafsız kalarak), hadi Frequentists kampını ziyaret edelim.
Sıkça İstatistik nedir?
Bu, çoğu insanın istatistikte öğrendiği ilk çıkarımsal tekniktir. Sık kullanılan istatistikler, bir olayın (hipotez) aynı koşullar altında sıklıkla meydana gelme olasılığını hesaplar.
Sıklıkçı yaklaşımı kullanan A/B hipotez testi şu adımları takip eder:
- Bazı hipotezler açıklayın. Tipik olarak, sıfır hipotezi, yeni "B" varyantının orijinal "A"dan daha iyi olmadığı, alternatif hipotez ise bunun tersini beyan eder.
- Sıralı test yaklaşımları kullanmıyorsanız, istatistiksel bir güç hesaplaması kullanarak önceden bir örnek boyutu belirleyin . İstatistiksel gücü, mevcut dönüştürme oranını ve saptanabilir minimum etkiyi dikkate alan bir örnek boyutu hesaplayıcısı kullanın.
- Testi çalıştırın ve her bir varyasyonun önceden belirlenmiş numune boyutuna maruz kalmasını bekleyin.
- En az sıfır hipotezi (p-değeri) altındaki veriler kadar aşırı bir sonuç gözlemleme olasılığını hesaplayın . Boş hipotezi reddedin ve p değeri < %5 ise yeni varyantı üretime dağıtın.
Bu Bayesian ile nasıl karşılaştırılır? Bakalım…
Bayesian vs Frequentist A/B Testi
Bu, istatistiksel çıkarımın kullanıldığı her yerde meşhur bir tartışmadır. Ve dürüst olmak gerekirse, bu anlamsız. Her ikisinin de, kullanmanın en iyi yöntemi olduğu yararları ve örnekleri vardır.
Her iki kamptaki destekçilerin çoğunun size düşündüreceğinin aksine, birkaç yönden benzerler ve yaklaşımları farklı olsa da hiçbiri gerçeğe diğerinden daha yakın değil.
Örneğin, A/B testine uygulandığında, belirli bir yöntem, iş büyümesine neden olacak eylem planı açısından size mutlak ve doğru bir tahmin vermez. Bunun yerine, A/B testi, karar verme riskini ortadan kaldırmanıza yardımcı olur.
Verilerinizi nasıl analiz ederseniz edin – Bayesian veya Frequentist yaklaşımları kullanarak – haklı olduğunuza dair bir miktar kesinlik ile hamleler yapabilirsiniz.
Ve bu nedenle, her iki istatistiksel model de geçerlidir. Bayesian bir hız avantajına sahip olabilir, ancak Frequentist'ten daha fazla hesaplama gerektirir.
Diğer farklılıklara göz atın…
Sıkça Kullanılan Çerçeve
Çoğumuz, giriş istatistik derslerinden sık kullanılan yaklaşıma aşinayız. Yukarıdaki metodolojiyi tanımladık - sıfır hipotezi ilan etmekten, örnek boyutunu belirlemekten, rastgele bir deney yoluyla veri toplamaktan ve son olarak istatistiksel olarak anlamlı bir sonuç gözlemlemekten.
Sıklıkçılıkta, olasılığı temelde tekrarlanan olayların sıklıklarıyla ilişkili olarak görüyoruz. Yani, adil bir yazı tura atışında, bir Frequentist, yeterince sık tahminde bulunursa, zamanın %50'sinde tura alacağına ve tura için de aynı olduğuna inanır.
Sıkçı zihniyet: "Deneyimi aynı koşullarda tekrar tekrar yaparsam, yöntemimin doğru yanıtı alma şansı nedir?"
Bayes Çerçevesi
Sıklıkçı yaklaşım, her bir değişken için popülasyon parametresini (bilinmeyen) bir sabit olarak ele alırken, Bayes yaklaşımı, her parametre değerini bir miktar olasılık dağılımına sahip rastgele bir değişken olarak modeller.
Burada, doğrudan ilgilenilen parametreler için olasılık dağılımlarını (ve dolayısıyla beklenen değerleri) hesaplarsınız.
Ve her bir değişken için olasılık dağılımını modellemek için, deney sonuçlarını ilgili ölçüm hakkında sahip olduğumuz herhangi bir ön bilgiyle birleştirmek için Bayes kuralına güveniyoruz. Önceden bir eşlenik kullanarak hesaplamaları basitleştirebiliriz.
Alex Birkett, Bayes algoritmasını şu şekilde özetledi:
- Bir parametre hakkındaki öznel inançlarınızı içeren önceki dağılımı tanımlayın. Önceki bilgilendirici veya bilgilendirici olmayabilir.
- Veri toplamak.
- Sonsal bir dağılım elde etmek için önceki dağılımınızı Bayes teoremini kullanarak verilerle güncelleyin (ancak Bayes kuralını açıkça kullanmadan Bayes yöntemlerine sahip olabilirsiniz - bkz. parametrik olmayan Bayesian). Sonsal dağılım, verileri gördükten sonra parametre hakkındaki güncellenmiş inançlarınızı temsil eden bir olasılık dağılımıdır.
- Sonsal dağılımı analiz edin ve özetleyin (ortalama, medyan, sd, nicelikler…).
Kısacası, Bayes deneycisi kendi bakış açısına ve olasılığın onlar için ne anlama geldiğine odaklanır. Görüşleri gözlemlenen verilerle gelişir. Öte yandan, sık sık kullananlar, doğru cevabın orada bir yerde olduğuna inanıyor.

Frequentist ve Bayesian tartışmasının A/B test sonrası analizini o kadar fazla etkilemediğini anlayın. İki kamp arasındaki büyük farklar, daha çok neyin test edilebileceği ile ilgilidir.
Olasılık istatistikleri genellikle sonraki analizlerde büyük ölçüde kullanılmaz. Bayesian-Frequentist argümanı, A/B paradigmasında test edilecek değişkenlerin seçimi ile ilgili olarak daha uygulanabilir, ancak orada bile çoğu A/B testçisi, araştırma hipotezlerini, olasılıkları ve güven aralıklarını cehenneme çevirmektedir .
Dr. Rob Balon'dan CXL'e
Georgi daha da detaylandırıyor:
Birden fazla çevrimiçi Bayes hesaplayıcısı ve tümü bilgilendirici olmayan öncelikler olarak adlandırılan bir Bayes istatistiksel motoru uygulayan en az bir büyük A/B test yazılımı satıcısı vardır (biraz yanlış adlandırma, ancak buna girmeyelim). Çoğu durumda, bu araçlardan elde edilen sonuçlar, aynı veriler üzerinde sık yapılan bir testin sonuçlarıyla sayısal olarak örtüşmektedir. Diyelim ki Bayes aracı, 'B'nin A'dan daha iyi olması için %96 olasılık' gibi bir şey rapor ederken, sık kullanılan araç, %96'lık bir güven düzeyine karşılık gelen 0.04'lük bir p değeri üretecektir.
Yukarıdaki gibi, bazılarının kabul etmek isteyeceğinden çok daha yaygın olan bir durumda, her iki yöntem de aynı çıkarıma yol açacaktır ve yorum farklı olsa bile belirsizlik düzeyi aynı olacaktır.
Bir Bayesci bu sonuç hakkında ne söylerdi? Ön bilgi olmayan bir senaryoyu görüntülerken p-değerini uygun bir sonsal olasılığa dönüştürüyor mu? Yoksa Bayes testlerinin tüm bu uygulamaları, kendi başına bilgilendirici olmayan bir ön bilgi kullanmak için yanlış yönlendiriliyor mu?
Diğer kampa taş atmak için bir kamp seçip siper arkasında bir yer bulmaya gerçekten gerek yok. Her iki çerçevenin de aynı sonuçları ürettiğine dair kanıtlar bile var. Seçtiğiniz yol ne olursa olsun, hedef muhtemelen aynı olacaktır. Frequentist vs Bayesian ile oraya nasıl ulaşabileceğinize bağlı.
Örneğin:
- Bayes testinin daha hızlı olduğunu ve etkileşimli deneyler için tercih edilen seçim olduğunu gösteren veriler var:
Bayes paradigması, deneycilerin inancı resmi olarak nicelleştirmesine ve ek bilgileri dahil etmesine izin verdiğinden, geleneksel istatistiksel analizden daha hızlıdır.
Bir Bayesian A/B testi simülasyonunda, karar kriteri ayarlandığında (yani, hatalara karşı toleransın arttırılması), deneylerin %75'i, geleneksel yaklaşımın gerektirdiği gözlemlerin %22.7'sinde (%5 anlamlılık düzeyinde) sonuçlandırılmıştır. Ve sadece %10 tip II hata kaydetti. - Bayesian ayrıca daha bağışlayıcı olarak kabul edilirken, Frequentist riskten kaçınır:
Birçok Frequentist testi %95'lik bir istatistiksel anlamlılık kullanırken, Bayesçiler bundan daha azıyla tatmin olabilir. Beklenen kayba bağlı olarak bir varyantın kontrolü yenme şansı %78 ise, o varyantı dağıtmak doğru bir karar olabilir.
Eğer yanılıyorsanız ve beklenen kayıp yüzde birin altındaysa, bu birçok işletme için oldukça önemsiz bir zarardır. Bu dağınık yaklaşım, çok düşük riskli senaryolarda hızlı karar vermek için daha uygun olabilir. - Ancak, Bayes simülasyonları ve hesaplamaları, hesaplama açısından ağırdır:
Frequentist, diğer taraftan, kalem ve kağıt tabanlıdır. Uyarı: A/B test aracınız Bayesian kullanıyorsa ve verilerinize hangi varsayımların eklendiğini bilmiyorsanız, satıcınızın size verdiği "cevaba" güvenemezsiniz. Bir tutam tuzla birlikte alın. Ve kendi analizinizi yapın.
Bayesian ile her şey güneş ışığı ve gökkuşakları değil. Georgi'nin bu soru listesiyle işaret ettiği gibi:
- "Önceki olasılık ve olabilirlik fonksiyonunun çarpımını mı almak istiyorsunuz?"
- “Bir çıktı olarak önceki olasılıkların ve verilerin karışımını mı istiyorsunuz?”
- “Çıktıyı üretmek için verilerle karıştırılmış öznel inançlar mı istiyorsunuz?” (bilgilendirici öncelikler kullanılıyorsa)
- "Gerçek verilerle karıştırılmış olarak yüksek oranda kesin olduğu varsayılan ön bilgilerin bulunduğu istatistikleri sunmaktan çekinmez misiniz?"
Bunların hepsi, meslekten olmayanların terimleriyle Bayes istatistiklerinin yönleridir.
Bayes İstatistikleri A/B Testinde Size Gerçekte Ne Diyor?
A/B testinizi, bir değişikliğin, dönüşüm oranı veya ziyaretçi başına gelir gibi ilgi metriğinizi nasıl etkilediğine ilişkin bilgiler verecek şekilde tasarladınız.
Bayes istatistikleriyle çalışan bir araç kullandığınızda, sonuçlarınızın ne anlama geldiğini anlamak önemlidir çünkü “B kazanandır” tam olarak çoğu insanın düşündüğü anlamına gelmez.
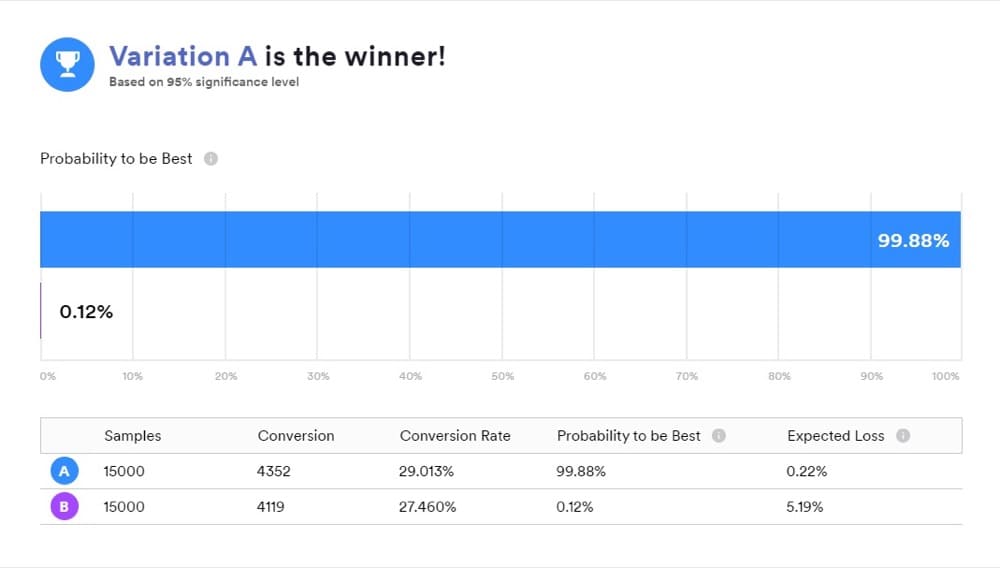
Sonuçları sunmanın uygun bir yolu, ancak testinizin ortaya çıkardığı şey bu değil. Bunun yerine, istediğiniz cevaplar “A” ve “B”nin sonsal karşılaştırmalarındadır.
İşte 3 karşılaştırma yöntemi:
En İyi Olma Olasılığı (P2BB)
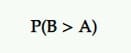
Bu, Bayesian A/B testinde kazanan ilan eden olasılıktır.
En iyi olma olasılığı olan değişken, diğerinden daha iyi performans göstermeye devam etme olasılığı en yüksek olandır.
Bu, orijinal ve sorgulayıcıdan ilgi ölçüsünün bir dizi sonsal örneğinden hesaplanır.
Bu nedenle, örneğin, B'nin dönüşüm oranlarınızı artırma olasılığı en yüksekse, örneğin B kazanan olarak ilan edilir.
Beklenen Artış
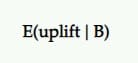
Öyleyse, kazanan B ise, ondan ne kadar yükselme beklemeliyiz? Testte gördüğümüz aynı sonuçları vermeye devam edecek mi?
Beklenen yükselişin sağlamaya çalıştığı içgörü budur. Bir dizi arka örnek verildiğinde, A yerine B'yi seçmenin beklenen artışı, yüzde artışının güvenilir aralığı (veya ortalaması) olarak tanımlanır.
A/B testinde, bunu genellikle kontrole karşı meydan okuyan olarak karşılaştırırız. Bu nedenle, yarışmacı kaybederse, negatif değerlerle (-%11,35 gibi) ve kazanırsa pozitif değerlerle (+%9,58 gibi) temsil edilir.
Beklenen Kayıp
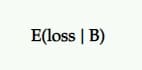
B'nin A'dan daha iyi olma olasılığı %100 olmadığından, A yerine B'yi seçerseniz bir kayıp kaydetme şansınız vardır. Bu, beklenen kayıp olarak temsil edilir ve tıpkı beklenen artışta olduğu gibi, kontrole karşı meydan okuyanın bakış açısı.
Size P2BB varyantınızı (yani, beyan edilen kazananı) seçme riskini söyler.
Efsanelere dalmadan önce, analitik efsanesi Georgi Georgiev'e çok teşekkür ederiz. A/B testinde sık kullanılan vs Bayes çıkarımı ve Bayes olasılık ve istatistiklerine ilişkin derinlemesine analizleri bir sonraki bölüme ilham verdi.
Bayes İstatistiklerinden Kaçınılması Gereken Mitler
Neredeyse gereksiz olduğu kadar eski bir rekabetle, Bayesian ve Frequentist tartışması çok fazla girdi topladı - ve birçok efsaneye yol açtı.
Bu efsanelerin en büyüğü (mit # 2), bir yaklaşımın neden diğerinden daha iyi olduğunu size anlatmak için A/B test aracı satıcıları tarafından desteklenir.
Ancak yukarıdaki bölümleri okuduktan sonra daha iyi bilirsiniz.
Gelin bu mitlerdeki boşlukları ortaya çıkaralım.
Efsane 1: Bayesçiler Varsayımlarını Belirtirler, Sıkça Kullananlar Söylemez
Bu, Bayescilerin önceki dağılımlar şeklinde varsayımlarda bulunduğunu ve bunların değerlendirmeye açık olduğunu göstermektedir. Ancak Sıkça kullanılanlar, matematiğin ortasında gizlenmiş varsayımlarda bulunurlar.
Neden yanlış: Bayesçiler ve Frekansçılar benzer temel varsayımlarda bulunurlar, tek fark Bayesçilerin matematiğin üstüne ek varsayımlar yapmasıdır.
Sık kullanılan modeller, dağılımın şekli, gözlemler arasındaki etkinin homojenliği veya heterojenliği ve gözlemin bağımsızlığı gibi matematikte varsayımları kullanır. Ve gizli değiller. Aslında, istatistiksel toplulukta geniş çapta tartışılırlar ve her sık kullanılan istatistiksel test için belirtilirler.
Gerçek: Sıkça kullananlar varsayımlarını açıkça belirtirler ve varsayımları test etmek için bir adım daha ileri giderler: normallik testleri, uygunluk testi (bunun altında örneklem oranı uyumsuzluğu testine sahibiz) ve daha fazlası.
Efsane #2. Bayes Yöntemleri Size Aslında İstediğiniz Cevapları Verir
Buradaki yanlış anlama, p-değerleri ve güven aralıklarının testçilere ne bilmek istediklerini söylemezken, arkadaki olasılıklar ve güvenilir aralıkların söylediğidir. İnsanlar gibi şeyleri bilmek ister
- B'nin A'dan daha iyi performans gösterme olasılığı ve
- Sonucun tesadüf olmama olasılığı.
P değerleri ve hipotez testleri (doğrudan çıkarım) bu bilgiyi sağlamaz, ancak ters çıkarım sağlar.
Neden yanlış: Bu bir dilbilim sorunudur. Genel olarak, istatistikçi olmayanlar “olasılık”, “şans” ve “olasılık” gibi terimleri kullandıklarında, bunları teknik anlamlarını göz önünde bulundurarak kullanmazlar. Daha derine inin ve onların düz çıkarım konusunda olduğu kadar ters çıkarım konusunda da kafalarının karışık olduğunu göreceksiniz.
Georgi Georgiev'e göre, bunun gibi sorular ortaya çıkmaya başlıyor:
- “ Önceki olasılık nedir ? Hangi değeri getiriyor?”
- "Olabilirlik fonksiyonu nedir?"
- “Hangi 'önceki' olasılık, önceden veri yok mu?”
- "Önceki bir olasılığın seçimini nasıl savunabilirim?"
- "Bu karışımlardan herhangi biri olmadan, verilerin söylediğini iletmenin bir yolu var mı?"
Gerçek: Testçilerin teknik terimleri yanlış yorumlamalarından ziyade bilmek istediklerine dair daha iyi bir anlayış olmalıdır. P değerleri, güven aralıkları ve diğerleri, toplanan verilerle sonuçların ne kadar iyi araştırıldığını size söyler. Sübjektif, test edilmemiş önceki varsayımların etkisi olmadan bir kesinlik ölçüsü sağladılar.
Efsane #3: Bayes Çıkarımı, Belirsizliği Sıkça Çıkarımdan Daha İyi Anlatmanıza Yardımcı Oluyor
Çünkü testlerin sonuçları daha “anlamlı” içgörüler üretiyor.
Neden yanlış: Hem Frequentist hem de Bayes yaklaşımlarının, kesinliği ve A/B testinizin sonuçlarını iletmenize yardımcı olacak benzer araçları vardır.
| sık sık | Bayes | ||||||||||
| ● Puan tahminleri | ● Puan tahminleri | ||||||||||
| ● P-değerleri | ● Güvenilir aralıklar | ||||||||||
| ● Güven aralıkları | ● Bayes faktörleri | ||||||||||
| ● P-değeri eğrileri | ● Arka dağılımlar (aynı görevi tamamla Frequentist eğrileri gibi) | ||||||||||
| ● Güven eğrileri | |||||||||||
| ● Önem eğrileri vb. |
Gerçek: Her şey onları nasıl kullandığınıza bağlı. Her iki yöntem de belirsizliğin iletilmesinde eşit derecede etkilidir. Ancak, belirsizlik ölçüsünü nasıl sundukları konusunda farklılıklar vardır.
Efsane #4. Bayes A/B Testi Sonuçları Göz Atmaya Bağışıklıdır
Bazı Bayes istatistikçileri, “açık bir kazanan” gördüğünüzde bir Bayes testini durdurabileceğinizi ve bunun nihai sonuçta çok az fark yarattığını iddia ediyor.
Muhtemelen bunun Frequentist testlerinde kabul edilemez olduğunu biliyorsunuzdur, bu nedenle Bayesian ile karşılaştırıldığında bir dezavantaj olarak sayılır. Ama gerçekten öyle mi?
Neden yanlış: Journal of the Royal Statistical Society'de yayınlanan “Veri Birikimi Üzerine Tekrarlanan Önem Testleri” başlıklı 1969 tarihli bir çalışmada Armitage ve ark. sonuca dayalı isteğe bağlı durdurmanın hata olasılığını nasıl artırdığını gösterdi.
Bir kazanan fark ettiğinizde duramaz, sonunuzu güncelleyemez ve Bayes analizinin çalışma şeklini ayarlamadan bir sonraki önceliğiniz olarak kullanamazsınız.
Gerçek: Peeking, Bayes çıkarımını Frequentist kadar etkiler (eğer doğru yapmak istiyorsanız).
Efsane #5. Sabit Bir Örnek Boyutunu Beklemeniz Gerektiğinden Sıkça Kullanılan İstatistikler Verimsizdir
CRO topluluğunun bazı üyeleri, sık yapılan istatistiksel testlerin sabit, önceden belirlenmiş bir örneklem boyutuyla yapılması gerektiğine inanır, aksi takdirde sonuçlar geçersizdir.
Sonuç olarak, istediğiniz sonuçları elde etmek için gereğinden fazla beklersiniz.
Neden yanlış: Sık kullanılan istatistikler yaklaşık yetmiş yıldır bu şekilde kullanılmamaktadır. Sık yapılan sıralı testler ile önceden belirlenmiş sabit bir süreye ihtiyacınız yoktur.
Gerçek: Günümüzde daha popüler olan sıralı testler, tip I ve tip II hataları dengelemek için maksimum bir örneklem büyüklüğü gerektirir, ancak kullanılan gerçek örnek boyutu, gözlemlenen sonuca bağlı olarak durumdan duruma değişir.
Peki, Bayesian mı yoksa Frequentist mi Seçmelisiniz? İkisinin de Yeri Vardır.
Taraf seçmeye gerek yok. Her iki yöntemin de yeri vardır. Örneğin, güncellenmiş öncelikleri kullanan ve hızlı sonuçlara ihtiyaç duyan uzun vadeli bir proje, Bayes yaklaşımıyla daha iyi sonuç verir.
Frequentist yöntemi ise sonuçlarında önemli miktarda tekrarlanabilirlik gerektiren projeler için en uygun yöntemdir. Birçok veri setine sahip birçok kişinin kullanacağı yazılım yazarken olduğu gibi.
Google Karar İstihbaratı Başkanı Cassie Kozyrkov'un dediği gibi, “İstatistik, belirsizlik altında fikrinizi değiştirme bilimidir”.
Bayesian vs Frequentist İstatistik özet videosunda şunları söyledi:
"Sık sık kullanılan ve Bayesci tartışmayı alabilir ve her şeyi, fikrinizi değiştirdiğiniz şeye indirgeyebilirsiniz. Sık sık insanlar eylemler hakkında fikirlerini değiştirirler, tercih edilen bir varsayılan eylemleri vardır - belki herhangi bir inançları yoktur - ama cehalet altında sevdikleri bir eylemleri vardır ve sonra sorarlar, “Kanıtım [veya verilerim] fikrimi değiştiriyor mu? bu eylem?" “Kanıtlarıma dayanarak bunu yaparken kendimi gülünç mü hissediyorum?”
Bayesçiler ise fikirlerini farklı bir şekilde değiştirirler. Öncelikli olarak adlandırılan, matematiksel olarak ifade edilen bir kişisel görüşle başlarlar ve sonra sorarlar, "Bazı kanıtları birleştirdikten sonra sahip olmam gereken mantıklı görüş nedir?" Ve böylece, Sık sık görüşenler eylemler hakkındaki fikirlerini değiştirirler, Bayesçiler ise inançlar hakkındaki fikirlerini değiştirirler.
Ve karar verme sürecinizi nasıl çerçevelemek istediğinize bağlı olarak, bir kamp yerine diğerine gitmeyi tercih edebilirsiniz.”
Sonunda, hepimiz benzer sonuçlara doğru gidiyoruz - fark, bu sonuçların size nasıl sunulduğudur.
Frekansçı ve Bayes çıkarımı, girdilerin istatistiksel problemler olduğu programlama işlevleri olsaydı, ikisi kullanıcıya geri döndüklerinde farklı olurdu. Sık çıkarım işlevi, bir tahmini temsil eden bir sayı döndürür (tipik olarak örnek ortalama vb. gibi bir özet istatistik), oysa Bayes işlevi olasılıkları döndürür.
“Olasılıksal Programlama ve Hackerlar için Bayes Yöntemleri” kitabından alıntı
Pek doğru olmayan, birinin diğerinden daha pratik sonuçlar verdiği iddiasıdır.
Anahtar Paket Servis
A/B testindeki Bayes istatistikleri 4 farklı adımdan oluşur:
- Önceki dağıtımınızı tanımlayın
- İnançlarınızı yansıtan istatistiksel bir model seçin
- Denemeyi çalıştırın
- İnançlarınızı güncellemek ve bir sonraki dağılımı hesaplamak için sonuçları kullanın
Sonuçlarınız sizi anlayışlı olasılıklara yönlendirecektir. Böylece hangi varyantın en iyi olma olasılığının en yüksek olduğunu, beklenen kaybınızı ve beklenen yükselişinizi bileceksiniz.
Bunlar genellikle sizin için Bayes istatistiklerini kullanan çoğu A/B test aracı tarafından yorumlanır. Ancak kapsamlı bir deneyci, bu sonuçları daha iyi anlamak için bir test sonrası analizi yapacaktır.
Buraya kadar geldiğiniz için, işte size eğlenceli bir gerçek: Herkesin aşina olduğu Thomas Bayes portresini biliyor musunuz? Bu:

Kimse onun o olduğundan %100 emin değil.