ข้อผิดพลาด Type I และ Type II: ข้อผิดพลาดที่หลีกเลี่ยงไม่ได้ในการเพิ่มประสิทธิภาพ

ข้อผิดพลาดประเภทที่ 1 และประเภทที่ 2 เกิดขึ้นเมื่อคุณระบุผู้ชนะในการทดสอบของคุณอย่างไม่ถูกต้อง หรือไม่สามารถระบุผู้ชนะได้ ด้วยข้อผิดพลาดทั้งสอง คุณจะลงเอยด้วยสิ่งที่ดูเหมือนว่าจะใช้ได้ผลหรือไม่ และไม่ใช่กับผลลัพธ์ที่แท้จริง

ผลการทดสอบที่แปลผิดไม่เพียงส่งผลให้เกิดความพยายามในการเพิ่มประสิทธิภาพที่ผิดพลาดเท่านั้น แต่ยังอาจทำให้โปรแกรมเพิ่มประสิทธิภาพของคุณเสียหายในระยะยาวอีกด้วย

เวลาที่ดีที่สุดในการตรวจจับข้อผิดพลาดเหล่านี้คือก่อนที่คุณจะสร้างมันขึ้นมาด้วยซ้ำ! มาดูกันว่าคุณจะหลีกเลี่ยงข้อผิดพลาดประเภท I และประเภท II ได้อย่างไรในการทดสอบการเพิ่มประสิทธิภาพของคุณ

แต่ก่อนหน้านั้น มาดูสมมติฐานว่างๆ… เพราะ เป็นการปฏิเสธที่ผิดพลาดหรือการไม่ปฏิเสธสมมติฐานว่างที่ทำให้เกิดข้อผิดพลาดประเภทที่ 1 และประเภท II

สมมติฐานว่าง: ​H0

เมื่อคุณตั้งสมมติฐานการทดสอบ คุณจะไม่ข้ามเพื่อแนะนำโดยตรงว่าการเปลี่ยนแปลงที่เสนอจะย้ายเมตริกหนึ่งๆ

คุณเริ่มด้วยการบอกว่าการเปลี่ยนแปลงที่เสนอจะไม่ส่งผลกระทบต่อเมตริกที่เกี่ยวข้องเลย ซึ่งไม่เกี่ยวข้องกัน

นี่คือสมมติฐานว่าง (H0) ของคุณ H0 อยู่เสมอว่าไม่มีการเปลี่ยนแปลง นี่คือสิ่งที่คุณเชื่อโดยค่าเริ่มต้น... จนกว่า (และถ้า) การทดสอบของคุณจะหักล้าง

และสมมติฐานทางเลือกของคุณ (Ha หรือ H1) คือมีการเปลี่ยนแปลงในเชิงบวก H0 และ Ha มักจะตรงกันข้ามทางคณิตศาสตร์ Ha คือสิ่งที่คุณคาดหวังว่าการเปลี่ยนแปลงที่เสนอจะสร้างความแตกต่าง เป็นสมมติฐานทางเลือกของคุณ และนี่คือสิ่งที่คุณกำลังทดสอบกับการทดสอบของคุณ

ตัวอย่างเช่น หากคุณต้องการเรียกใช้การทดสอบในหน้าการกำหนดราคาของคุณและเพิ่มวิธีการชำระเงินอื่นเข้าไป ขั้นแรกคุณจะต้องสร้างสมมติฐานว่างว่า: วิธีการชำระเงินเพิ่มเติมจะไม่มีผลกระทบต่อยอดขาย สมมติฐานอื่นของคุณจะอ่านว่า: วิธีการชำระเงินเพิ่มเติมจะเพิ่มยอดขาย

อันที่จริง การทำการทดสอบเป็นการท้าทายสมมติฐานว่างหรือสถานะที่เป็นอยู่

ข้อผิดพลาด Type I และ Type II เกิดขึ้นเมื่อคุณปฏิเสธหรือปฏิเสธสมมติฐานว่างโดยผิดพลาด

การทำความเข้าใจข้อผิดพลาดประเภทที่ 1

ข้อผิดพลาดประเภทที่ 1 เรียกว่าผลบวกลวงหรือข้อผิดพลาดอัลฟ่า

ในอินสแตนซ์ข้อผิดพลาดประเภทที่ 1 ของการทดสอบสมมติฐาน การทดสอบการเพิ่มประสิทธิภาพหรือการทดสอบของคุณ * ปรากฏว่าประสบความสำเร็จ* และคุณ (ผิดพลาด) สรุปว่ารูปแบบที่คุณกำลังทดสอบนั้นทำแตกต่างไปจากเดิม (ดีขึ้นหรือแย่ลง) กว่าเดิม

ในข้อผิดพลาดประเภทที่ 1 คุณเห็นการเพิ่มขึ้นหรือลดลง ซึ่งเกิดขึ้นเพียงชั่วคราวและไม่น่าจะคงอยู่ในระยะยาว และจบลงด้วยการปฏิเสธสมมติฐานว่างของคุณ (และยอมรับสมมติฐานทางเลือกของคุณ)

การปฏิเสธสมมติฐานว่างอย่างผิดพลาดอาจเกิดขึ้นได้จากหลายสาเหตุ แต่เหตุผลหลักคือการพยายาม แอบดู (เช่น การดูผลลัพธ์ของคุณในระหว่างช่วงเวลาหรือเมื่อการทดสอบยังทำงานอยู่) และเรียกการทดสอบเร็วกว่าเกณฑ์การหยุดที่กำหนดไว้

วิธีการทดสอบหลายๆ วิธีกีดกันการฝึกแอบมอง เนื่องจากการดูผลลัพธ์ระหว่างกาลอาจนำไปสู่ข้อสรุปที่ผิดพลาดซึ่งส่งผลให้เกิดข้อผิดพลาดประเภทที่ 1

ต่อไปนี้คือวิธีสร้างข้อผิดพลาดประเภทที่ 1

สมมติว่าคุณกำลังเพิ่มประสิทธิภาพหน้า Landing Page ของเว็บไซต์ B2B และตั้งสมมติฐานว่าการเพิ่มป้ายหรือรางวัลเข้าไปจะช่วยลดความวิตกกังวลของผู้มีแนวโน้มจะเป็นลูกค้า ซึ่งจะเพิ่มอัตราการส่งแบบฟอร์มของคุณ (ส่งผลให้มีลูกค้าเป้าหมายมากขึ้น)

ดังนั้น สมมติฐานว่างสำหรับการทดสอบนี้จึงกลายเป็น: การ เพิ่มป้ายไม่มีผลกระทบต่อการกรอกแบบฟอร์ม

เกณฑ์การหยุดสำหรับการทดสอบดังกล่าวมักจะเป็นช่วงเวลาหนึ่งและ/หรือหลังจากเกิด Conversion X ขึ้นที่ระดับนัยสำคัญทางสถิติที่ตั้งไว้ ตามธรรมเนียมแล้ว นักเพิ่มประสิทธิภาพพยายามที่จะบรรลุเครื่องหมายความเชื่อมั่นทางสถิติ 95% เพราะจะทำให้คุณมีโอกาส 5% ที่จะทำให้เกิดข้อผิดพลาดประเภทที่ 1 ซึ่งถือว่าต่ำพอสำหรับการทดสอบการเพิ่มประสิทธิภาพส่วนใหญ่ โดยทั่วไป ยิ่งเมตริกนี้สูงเท่าใด โอกาสในการสร้างข้อผิดพลาดประเภทที่ 1 ก็จะยิ่งต่ำลงเท่านั้น

ระดับความมั่นใจที่คุณตั้งเป้าไว้จะเป็นตัวกำหนดความน่าจะเป็นที่คุณจะได้รับข้อผิดพลาดประเภทที่ 1 (α)

ดังนั้นหากคุณตั้งเป้าไปที่ระดับความเชื่อมั่น 95% ค่าของคุณสำหรับ α จะกลายเป็น 5% ที่นี่ คุณยอมรับว่ามีโอกาส 5% ที่ข้อสรุปของคุณอาจผิดพลาด

ในทางตรงกันข้าม หากคุณใช้ระดับความมั่นใจ 99% กับการทดสอบของคุณ ความน่าจะเป็นที่จะเกิดข้อผิดพลาดประเภทที่ 1 จะลดลงเหลือ 1%

สมมติว่าสำหรับการทดสอบนี้ คุณใจร้อนเกินไป และแทนที่จะรอให้การทดสอบสิ้นสุด คุณดูที่แดชบอร์ดของเครื่องมือทดสอบ (ดู!) เพียงวันเดียวในการทดสอบนั้น และคุณสังเกตเห็นการเพิ่มขึ้นที่ "ชัดเจน" — ว่าอัตราการกรอกแบบฟอร์มของคุณเพิ่มขึ้น 29.2% ด้วยระดับความมั่นใจ 95%

และแบม...

… คุณหยุดการทดลองของคุณ

… ปฏิเสธสมมติฐานว่าง (ตราว่าไม่มีผลกระทบต่อการขาย)

… ยอมรับสมมติฐานทางเลือก (ที่ป้ายเพิ่มยอดขาย)

… และวิ่งด้วยรุ่นที่มีป้ายรางวัล

แต่เมื่อคุณวัดโอกาสในการขายของคุณตลอดทั้งเดือน คุณจะพบว่าจำนวนนั้นใกล้เคียงกับสิ่งที่คุณรายงานด้วยเวอร์ชันดั้งเดิม ป้ายก็ไม่ได้สำคัญอะไรมาก และสมมุติฐานว่างก็อาจจะถูกปฏิเสธไปโดยเปล่าประโยชน์

สิ่งที่เกิดขึ้นที่นี่คือคุณสิ้นสุดการทดสอบเร็วเกินไปและปฏิเสธสมมติฐานว่างและลงเอยด้วยผู้ชนะที่ผิดพลาด — ทำให้เกิดข้อผิดพลาดประเภทที่ 1

หลีกเลี่ยงข้อผิดพลาดประเภทที่ 1 ในการทดลองของคุณ

วิธีหนึ่งที่แน่นอนในการลดโอกาสในการตีข้อผิดพลาดประเภทที่ 1 คือระดับความมั่นใจที่สูงขึ้น ระดับนัยสำคัญทางสถิติ 5% (แปลเป็นระดับความเชื่อมั่นทางสถิติ 95%) เป็นที่ยอมรับ การเดิมพันที่นักเพิ่มประสิทธิภาพส่วนใหญ่จะทำได้อย่างปลอดภัยเพราะที่นี่ คุณจะล้มเหลวในช่วง 5% ที่ไม่น่าจะเกิดขึ้นได้

นอกจากการกำหนดระดับความมั่นใจในระดับสูงแล้ว การทำการทดสอบให้นานเพียงพอก็เป็นสิ่งสำคัญ เครื่องคำนวณระยะเวลาการทดสอบสามารถบอกคุณได้ว่าคุณต้องทำการทดสอบนานแค่ไหน หากคุณปล่อยให้การทดสอบดำเนินไปตามที่ตั้งใจไว้ คุณจะลดโอกาสในการพบข้อผิดพลาดประเภทที่ 1 ลงอย่างมาก (เนื่องจากคุณใช้ระดับความมั่นใจสูง) การรอจนกว่าคุณจะบรรลุผลลัพธ์ที่มีนัยสำคัญทางสถิติจะช่วยให้แน่ใจว่ามีโอกาสน้อย (โดยปกติคือ 5%) ที่คุณปฏิเสธสมมติฐานว่างอย่างผิดพลาดและเกิดข้อผิดพลาดประเภทที่ 1 พูดอีกอย่างก็คือ ใช้ขนาดตัวอย่างที่ดี เพราะนั่นสำคัญต่อการได้ผลลัพธ์ที่มีนัยสำคัญทางสถิติ

นั่นคือทั้งหมดที่เกี่ยวกับข้อผิดพลาดประเภทที่ 1 ที่เกี่ยวข้องกับระดับความเชื่อมั่น (หรือความสำคัญ) ในการทดสอบของคุณ แต่มีข้อผิดพลาดอีกประเภทหนึ่งที่สามารถเล็ดลอดเข้ามาในการทดสอบของคุณได้ นั่นคือข้อผิดพลาดประเภท II

การทำความเข้าใจข้อผิดพลาดประเภท II

ข้อผิดพลาดประเภท II เรียกว่าข้อผิดพลาดเท็จหรือข้อผิดพลาดเบต้า

ตรงกันข้ามกับข้อผิดพลาดประเภทที่ 1 ในกรณีของข้อผิดพลาดประเภท II การทดลอง *ดูเหมือนจะไม่สำเร็จ (หรือสรุปไม่ได้)* และคุณ (อย่างผิด) สรุปว่ารูปแบบที่คุณกำลังทดสอบไม่ได้แตกต่างไปจากข้อผิดพลาดประเภทที่ 1 ต้นฉบับ.

ในข้อผิดพลาดประเภท II คุณจะไม่เห็นการยกหรือการลดลงจริง และจบลงด้วยการล้มเหลวในการปฏิเสธสมมติฐานว่างและปฏิเสธสมมติฐานทางเลือก

ต่อไปนี้เป็นวิธีสร้างข้อผิดพลาดประเภท II:

กลับไปที่เว็บไซต์ B2B เดิมจากด้านบน…

สมมติว่าคราวนี้ คุณตั้งสมมติฐานว่าการเพิ่มข้อจำกัดความรับผิดชอบการปฏิบัติตาม GDPR ที่ด้านบนสุดของแบบฟอร์มอย่างเด่นชัดจะกระตุ้นให้ผู้ที่มีแนวโน้มจะเป็นลูกค้ากรอกแบบฟอร์มมากขึ้น (ส่งผลให้มีลูกค้าเป้าหมายมากขึ้น)

ดังนั้น สมมติฐานว่างสำหรับการทดสอบนี้จะกลายเป็น: ข้อจำกัดความรับผิดชอบการปฏิบัติตาม GDPR ไม่ส่งผลต่อการกรอกแบบฟอร์ม

และสมมติฐานทางเลือกสำหรับสิ่งเดียวกันนั้นอ่านว่า: ข้อจำกัดความรับผิดชอบในการปฏิบัติตาม GDPR ส่งผลให้มีการกรอกแบบฟอร์มมากขึ้น

พลังทางสถิติของการทดสอบเป็นตัวกำหนดว่าสามารถตรวจจับความแตกต่างในประสิทธิภาพของเวอร์ชันดั้งเดิมและเวอร์ชันที่ท้าทายได้ดีเพียงใด หากมีการเบี่ยงเบนใดๆ ตามเนื้อผ้า นักเพิ่มประสิทธิภาพพยายามที่จะบรรลุเครื่องหมายอำนาจทางสถิติ 80% เพราะยิ่งตัวชี้วัดนี้สูงเท่าใด โอกาสในการสร้างข้อผิดพลาดประเภท II ก็ยิ่งต่ำลงเท่านั้น

กำลังทางสถิติใช้ค่าระหว่าง 0 ถึง 1 (และมักแสดงเป็น %) และควบคุมความน่าจะเป็นของข้อผิดพลาดประเภท II (β) ของคุณ คำนวณเป็น: 1 – β

ยิ่งพลังทางสถิติของการทดสอบของคุณสูงขึ้น ความน่าจะเป็นที่จะพบข้อผิดพลาดประเภท II ก็จะยิ่งต่ำลง

ดังนั้น หากการทดสอบมีพลังทางสถิติ 10% ก็อาจมีความอ่อนไหวต่อข้อผิดพลาดประเภท II ได้ ในขณะที่หากการทดสอบมีพลังทางสถิติ 80% ก็มีโอกาสน้อยที่จะสร้างข้อผิดพลาดประเภท II

อีกครั้ง คุณทำการทดสอบ แต่คราวนี้ คุณไม่สังเกตเห็นการเพิ่มขึ้นอย่างมีนัยสำคัญในการกรอกแบบฟอร์มของคุณ ทั้งสองเวอร์ชันรายงานว่ามี Conversion ใกล้เคียงกัน ด้วยเหตุนี้ คุณจึงหยุดการทดสอบและดำเนินการต่อในเวอร์ชันดั้งเดิมโดยไม่มีข้อจำกัดความรับผิดชอบของ GDPR

อย่างไรก็ตาม เมื่อคุณเจาะลึกข้อมูลลีดของคุณจากช่วงทดสอบ คุณพบว่าในขณะที่จำนวนลีดจากทั้งสองเวอร์ชัน (ต้นฉบับและผู้ท้าชิง) ดูเหมือนจะเหมือนกัน แต่เวอร์ชัน GDPR ทำให้คุณมีจำนวนเพิ่มขึ้นที่ดีและมีนัยสำคัญ ของผู้นำจากยุโรป (แน่นอน คุณสามารถใช้การกำหนดกลุ่มเป้าหมายเพื่อแสดงการทดสอบต่อลูกค้าเป้าหมายจากยุโรปเท่านั้น แต่นั่นเป็นอีกเรื่องหนึ่ง)

สิ่งที่เกิดขึ้นที่นี่คือคุณสิ้นสุดการทดสอบเร็วเกินไป โดยไม่ตรวจสอบว่าคุณได้รับพลังงานเพียงพอหรือไม่ ซึ่งทำให้เกิดข้อผิดพลาดประเภท II

การหลีกเลี่ยงข้อผิดพลาดประเภท II ในการทดลองของคุณ

เพื่อหลีกเลี่ยงข้อผิดพลาดประเภท II ให้เรียกใช้การทดสอบที่มีกำลังทางสถิติสูง พยายามกำหนดค่าการทดสอบของคุณเพื่อให้คุณสามารถบรรลุเครื่องหมายอำนาจทางสถิติอย่างน้อย 80% นี่เป็นระดับพลังทางสถิติที่ยอมรับได้สำหรับการทดสอบการปรับให้เหมาะสมส่วนใหญ่ ด้วยสิ่งนี้ คุณสามารถมั่นใจได้ว่าใน 80% ของกรณี อย่างน้อย คุณจะปฏิเสธสมมติฐานว่างที่เป็นเท็จได้อย่างถูกต้อง

ในการทำเช่นนี้ คุณต้องดูปัจจัยที่เพิ่มเข้าไป

ที่ใหญ่ที่สุดคือขนาดกลุ่มตัวอย่าง (โดยพิจารณาจากขนาดผลที่สังเกตได้) ขนาดกลุ่มตัวอย่างสัมพันธ์โดยตรงกับพลังของการทดสอบ ขนาดตัวอย่างที่ใหญ่หมายถึงการทดสอบกำลังสูง การทดสอบที่ด้อยประสิทธิภาพมีความเสี่ยงต่อข้อผิดพลาดประเภท II อย่างมาก เนื่องจากโอกาสในการตรวจจับความแตกต่างในผลลัพธ์ของผู้ท้าชิงและเวอร์ชันดั้งเดิมของคุณลดลงอย่างมาก โดยเฉพาะอย่างยิ่งสำหรับ MEI ที่ต่ำ (เพิ่มเติมเกี่ยวกับเรื่องนี้ด้านล่าง) ดังนั้นเพื่อหลีกเลี่ยงข้อผิดพลาดประเภท II ให้รอให้การทดสอบสะสมกำลังเพียงพอเพื่อลดข้อผิดพลาดประเภท II ตามหลักการแล้ว ในกรณีส่วนใหญ่ คุณต้องการเพิ่มกำลังอย่างน้อย 80%

อีกปัจจัยหนึ่งคือ ผลกระทบขั้นต่ำของความสนใจ (MEI) ที่คุณกำหนดเป้าหมายสำหรับการทดสอบของคุณ MEI (เรียกอีกอย่างว่า MDE) คือขนาดต่ำสุดของความแตกต่างที่คุณต้องการตรวจพบใน KPI ที่เป็นปัญหา หากคุณตั้งค่า MEI ต่ำ (เช่น การเพิ่มขึ้น 1.5% เป็นต้น) โอกาสในการพบข้อผิดพลาดประเภท II จะเพิ่มขึ้น เนื่องจากการตรวจจับความแตกต่างเพียงเล็กน้อยนั้นต้องใช้ขนาดตัวอย่างที่ใหญ่ขึ้นมาก (เพื่อให้ได้พลังงานเพียงพอ)

และสุดท้าย สิ่งสำคัญคือต้องสังเกตว่ามีแนวโน้มที่จะมีความสัมพันธ์แบบผกผันระหว่างความน่าจะเป็นที่จะทำให้เกิดข้อผิดพลาดประเภทที่ 1 (α) กับความน่าจะเป็นที่จะทำให้เกิดข้อผิดพลาดประเภท II (β) ตัวอย่างเช่น หากคุณลดค่าของ α เพื่อลดความน่าจะเป็นที่จะทำให้เกิดข้อผิดพลาดประเภท I (เช่น คุณตั้งค่า α ที่ 1% ซึ่งหมายถึงระดับความมั่นใจ 99%) พลังทางสถิติของการทดสอบของคุณ (หรือความสามารถของการทดสอบคือ β ของการตรวจจับความแตกต่างเมื่อมันมีอยู่) ก็ลดลงเช่นกัน ซึ่งจะเพิ่มความน่าจะเป็นของคุณที่จะได้รับข้อผิดพลาดประเภท II

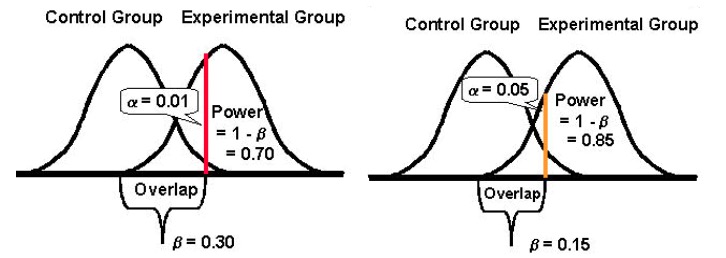
การยอมรับข้อผิดพลาดอย่างใดอย่างหนึ่งมากขึ้น: Type I และ II (& ความสมดุล)

การลดความน่าจะเป็นของข้อผิดพลาดประเภทหนึ่งจะทำให้ข้อผิดพลาดประเภทอื่นลดลง (หากข้อผิดพลาดทั้งหมดยังคงเหมือนเดิม)

ดังนั้น คุณต้องรับสายว่าข้อผิดพลาดประเภทใดที่คุณยอมรับได้มากกว่านี้

การทำข้อผิดพลาดประเภทที่ 1 และการเปิดตัวการเปลี่ยนแปลงสำหรับผู้ใช้ทั้งหมดของคุณอาจทำให้คุณต้องเสีย Conversion และรายได้ ซึ่งแย่กว่านั้นคืออาจเป็นตัวทำลาย Conversion ได้เช่นกัน

ในทางกลับกัน การทำข้อผิดพลาดประเภท II และการล้มเหลวในการเปิดตัวเวอร์ชันที่ชนะสำหรับผู้ใช้ทั้งหมดของคุณ อาจทำให้คุณต้องเสียค่าใช้จ่ายในการแปลงที่คุณอาจได้รับ

ข้อผิดพลาดทั้งสองมักมีค่าใช้จ่าย

อย่างไรก็ตาม ขึ้นอยู่กับการทดสอบของคุณ การทดสอบหนึ่งอาจเป็นที่ยอมรับของคุณมากกว่าการทดสอบอื่นๆ โดยทั่วไป ผู้ทดสอบพบ ข้อผิดพลาดประเภทที่ 1 ที่ร้ายแรงกว่าข้อผิดพลาดประเภท II ถึงสี่เท่า

หากคุณต้องการใช้วิธีการที่สมดุลมากขึ้น นักสถิติ Jacob Cohen แนะนำว่าคุณควรใช้พลังทางสถิติ 80% ที่มาพร้อมกับ “ ความสมดุลที่สมเหตุสมผลระหว่างความเสี่ยงอัลฟ่าและเบต้า ” (กำลัง 80% เป็นมาตรฐานสำหรับเครื่องมือทดสอบส่วนใหญ่เช่นกัน)

และเท่าที่มีนัยสำคัญทางสถิติ มาตรฐานตั้งไว้ที่ 95%

โดยพื้นฐานแล้ว มันเป็นเรื่องของการประนีประนอมและระดับความเสี่ยงที่คุณยินดีจะยอมรับ หากคุณต้องการลดโอกาสของข้อผิดพลาดทั้งสองอย่างแท้จริงให้เหลือน้อยที่สุด คุณสามารถไปที่ระดับความมั่นใจ 99% และพลัง 99% แต่นั่นก็หมายความว่าคุณจะต้องทำงานกับกลุ่มตัวอย่างขนาดใหญ่อย่างไม่น่าเชื่อในช่วงเวลาที่ดูเหมือนยาวนานชั่วนิรันดร์ นอกจากนี้ คุณยังเหลือขอบเขตสำหรับข้อผิดพลาดอยู่บ้าง

นานๆ ครั้ง คุณจะสรุปการทดลองอย่างผิดๆ แต่นั่นเป็นส่วนหนึ่งของกระบวนการทดสอบ — ต้องใช้เวลาสักพักกว่าจะเชี่ยวชาญสถิติการทดสอบ A/B การตรวจสอบและทดสอบซ้ำหรือติดตามการทดลองที่ประสบความสำเร็จหรือล้มเหลวเป็นวิธีหนึ่งในการยืนยันสิ่งที่คุณค้นพบหรือค้นพบว่าคุณทำผิดพลาด