Single Neuron Neural Network บน Python – ด้วยสัญชาตญาณทางคณิตศาสตร์

เผยแพร่แล้ว: 2021-06-21

มาสร้างเครือข่ายที่เรียบง่ายกันเถอะ — ง่ายมาก แต่เป็นเครือข่ายที่สมบูรณ์ - ด้วยเลเยอร์เดียว อินพุตเดียวเท่านั้น — และหนึ่งเซลล์ประสาท (ซึ่งเป็นเอาต์พุตด้วย) หนึ่งน้ำหนัก หนึ่งอคติ

มารันโค้ดกันก่อนแล้วค่อยวิเคราะห์ทีละส่วน

ลอกแบบโปรเจ็กต์ Github หรือเพียงแค่รันโค้ดต่อไปนี้ใน IDE ที่คุณชื่นชอบ

หากคุณต้องการความช่วยเหลือในการตั้งค่า IDE ฉันได้อธิบายขั้นตอนไว้ที่นี่

หากทุกอย่างเป็นไปด้วยดี คุณจะได้ผลลัพธ์นี้:

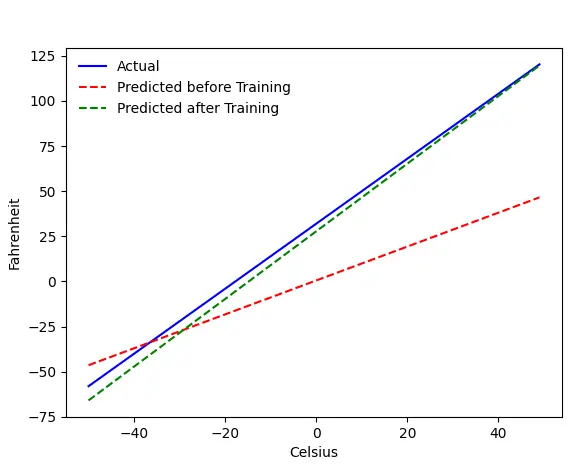
ปัญหา — ฟาเรนไฮต์จากเซลเซียส

เราจะฝึกเครื่องของเราให้ทำนายฟาเรนไฮต์จากเซลเซียส ดังที่คุณเข้าใจได้จากโค้ด (หรือกราฟ) เส้นสีน้ำเงินคือความสัมพันธ์ระหว่างเซลเซียสกับฟาเรนไฮต์จริง เส้นสีแดงคือความสัมพันธ์ที่ทำนายโดยเครื่องลูกของเราโดยไม่มีการฝึกใดๆ สุดท้าย เราฝึกเครื่องจักร และเส้นสีเขียวเป็นการทำนายหลังการฝึก

ดูบรรทัด#65–67 — ก่อนและหลังการฝึก คาดการณ์โดยใช้ฟังก์ชันเดียวกัน ( get_predicted_fahrenheit_values() ) แล้ว magic train() กำลังทำอะไรอยู่? ลองหากัน

โครงสร้างเครือข่าย

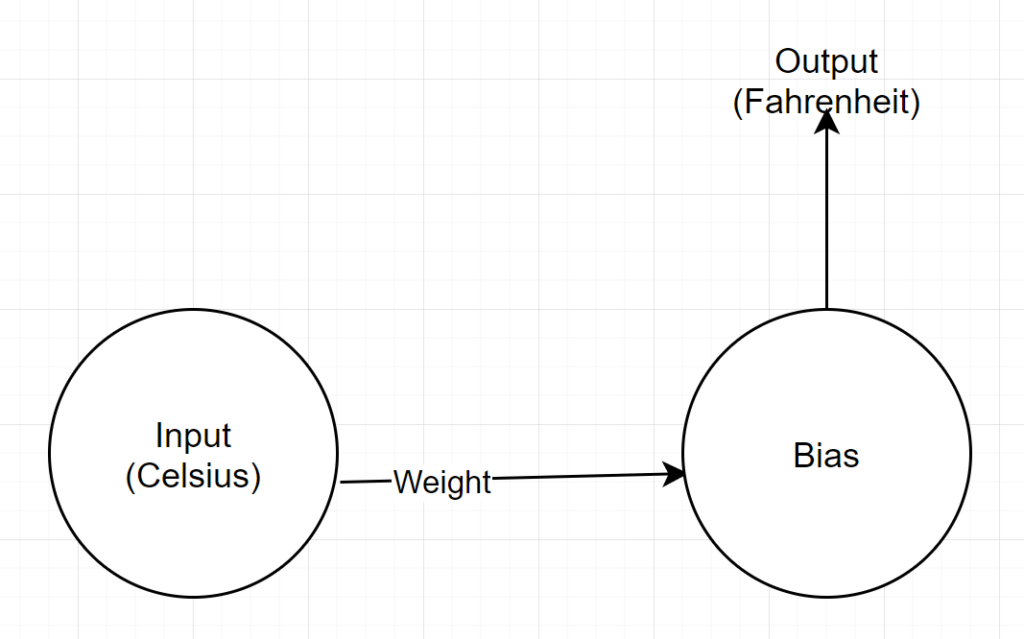
อินพุต: ตัวเลขที่แสดงเซลเซียส

น้ำหนัก: ทุ่นแทนน้ำหนัก

อคติ: ลอยแทนอคติ

ผลลัพธ์: ทุ่นที่แสดงถึงฟาเรนไฮต์ที่คาดการณ์ไว้

ดังนั้นเราจึงมีพารามิเตอร์ทั้งหมด 2 ตัว — 1 น้ำหนักและ 1 อคติ

การวิเคราะห์รหัส

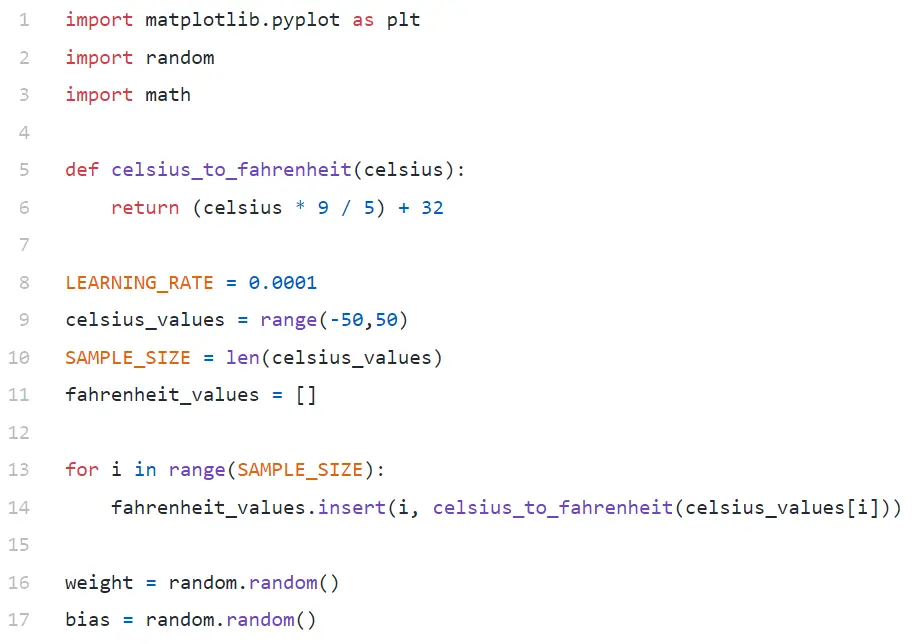
ในบรรทัด #9 เรากำลังสร้างอาร์เรย์ 100 หมายเลขระหว่าง -50 ถึง +50 (ยกเว้นฟังก์ชัน 50 — range ไม่รวมค่าขีดจำกัดบน)

ในบรรทัด #11–14 เรากำลังสร้างฟาเรนไฮต์สำหรับค่าเซลเซียสแต่ละค่า

ในบรรทัด #16 และ #17 เรากำลังเริ่มต้นน้ำหนักและอคติ

รถไฟ()

เรากำลังดำเนินการฝึกอบรมซ้ำ 10,000 ครั้งที่นี่ การทำซ้ำแต่ละครั้งประกอบด้วย:

ส่งต่อ (สาย#57) ผ่าน
ย้อนกลับ (บรรทัด#58) ผ่าน
update_parameters (บรรทัด#59)

หากคุณเพิ่งเริ่มใช้ python อาจดูแปลกๆ สำหรับคุณ — ฟังก์ชัน python สามารถคืนค่าได้หลายค่าเป็น tuple

โปรดสังเกตว่า update_parameters เป็นสิ่งเดียวที่เราสนใจ สิ่งอื่นที่เราทำที่นี่คือการประเมินพารามิเตอร์ของฟังก์ชันนี้ ซึ่งก็คือการ ไล่ระดับสี (เราจะอธิบายด้านล่างว่าการไล่ระดับสีคืออะไร) ของน้ำหนักและอคติของเรา

grad_weight: ทุ่นที่แสดงถึงการไล่ระดับสีของน้ำหนัก
grad_bias: ลอยแทนการไล่ระดับของอคติ

เราได้รับค่าเหล่านี้โดยการโทรย้อนกลับ แต่ต้องมีเอาต์พุต ซึ่งเราได้รับโดยการโทรไปข้างหน้าที่บรรทัด #57

ซึ่งไปข้างหน้า()

โปรดสังเกตว่าที่นี่ celsius_values และ fahrenheit_values เป็นอาร์เรย์ 100 แถว:

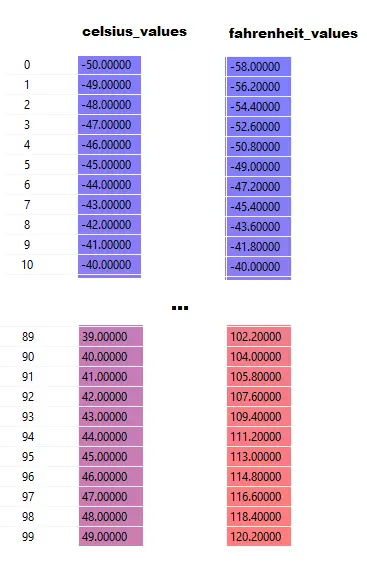
หลังจากรันบรรทัด#20–23 สำหรับค่าเซลเซียส ให้พูดว่า 42

ผลลัพธ์ = 42 * น้ำหนัก + อคติ

ดังนั้นสำหรับ 100 องค์ประกอบใน celsius_values เอาต์พุตจะเป็นอาร์เรย์ 100 องค์ประกอบสำหรับแต่ละค่าเซลเซียสที่สอดคล้องกัน

บรรทัด#25–30 กำลังคำนวณการสูญเสียโดยใช้ฟังก์ชันการสูญเสีย Mean Squared Error (MSE) ซึ่งเป็นเพียงชื่อแฟนซีของกำลังสองของส่วนต่างทั้งหมดหารด้วยจำนวนตัวอย่าง (100 ในกรณีนี้)

การสูญเสียเล็กน้อยหมายถึงการคาดการณ์ที่ดีขึ้น หากคุณยังคงสูญเสียการพิมพ์ในการทำซ้ำทุกครั้ง คุณจะเห็นว่าการพิมพ์นั้นลดลงเมื่อการฝึกอบรมดำเนินไป

สุดท้าย ในบรรทัด #31 เรากำลังส่งคืนผลลัพธ์และการสูญเสียที่คาดการณ์ไว้

ย้อนกลับ

เราสนใจเพียงแค่อัปเดตน้ำหนักและอคติของเราเท่านั้น ในการอัปเดตค่าเหล่านี้ เราต้องทราบการไล่ระดับสี และนั่นคือสิ่งที่เรากำลังคำนวณที่นี่

กำลังคำนวณการไล่ระดับสีของการแจ้งเตือนในลำดับที่กลับกัน ขั้นแรกให้คำนวณการไล่ระดับของเอาต์พุต จากนั้นสำหรับน้ำหนักและอคติ ดังนั้นชื่อ "backpropagation" เหตุผลก็คือ ในการคำนวณเกรเดียนท์ของน้ำหนักและอคติ เราจำเป็นต้องรู้เกรเดียนท์ของเอาต์พุต เพื่อที่เราจะสามารถใช้มันในสูตร กฎลูกโซ่ ได้

ตอนนี้เรามาดูกันว่ากฎการไล่ระดับสีและลูกโซ่คืออะไร

ไล่โทนสี

เพื่อความง่าย ให้พิจารณาว่าเรามีค่า celsius_values และ fahrenheit_values เพียงค่าเดียวคือ 42 และ 107.6 ตามลำดับ

ตอนนี้ รายละเอียดของการคำนวณในบรรทัด #30 กลายเป็น:

การสูญเสีย = (107.6 — (42 * น้ำหนัก + อคติ))² / 1

อย่างที่คุณเห็น การสูญเสียขึ้นอยู่กับ 2 พารามิเตอร์ — น้ำหนักและอคติ พิจารณาน้ำหนัก ลองนึกภาพ เราเริ่มต้นมันด้วยค่าสุ่ม เช่น 0.8 และหลังจากประเมินสมการข้างต้น เราได้ 123.45 เป็นค่าการ สูญเสีย จากมูลค่าการสูญเสียนี้ คุณต้องตัดสินใจว่าจะอัปเดตน้ำหนักอย่างไร คุณควรทำให้มันเป็น 0.9 หรือ 0.7?

คุณต้องอัปเดตน้ำหนักในลักษณะที่ในการทำซ้ำครั้งต่อไปคุณจะได้รับค่าการสูญเสียที่ต่ำกว่า (จำไว้ว่าการลดการสูญเสียเป็นเป้าหมายสูงสุด) ดังนั้น ถ้าน้ำหนักขึ้นเพิ่มการสูญเสีย เราก็จะลดลง และถ้าน้ำหนักขึ้นทำให้ลด เราก็เพิ่มค่ะ

ทีนี้ คำถามคือ เราจะรู้ได้อย่างไรว่าการเพิ่มน้ำหนักจะเพิ่มหรือลดการสูญเสีย นี่คือที่มาของการไล่ระดับสี เกรเดียนต์ถูกกำหนดโดยอนุพันธ์ จำจากแคลคูลัสระดับมัธยมปลายของคุณ ∂y/∂x (ซึ่งเป็นอนุพันธ์ย่อย/การไล่ระดับของ y เทียบกับ x) ระบุว่า y จะเปลี่ยนแปลงอย่างไรเมื่อมีการเปลี่ยนแปลงเล็กน้อยของ x

ถ้า ∂y/∂x เป็นบวก หมายความว่าการเพิ่มขึ้นเล็กน้อยใน x จะเพิ่ม y

ถ้า ∂y/∂x เป็นลบ หมายความว่าการเพิ่มขึ้นเล็กน้อยใน x จะลดลง y

ถ้า ∂y/∂x มีขนาดใหญ่ การเปลี่ยนแปลงเล็กน้อยของ x จะทำให้เกิดการเปลี่ยนแปลงครั้งใหญ่ใน y

ถ้า ∂y/∂x น้อย การเปลี่ยนแปลงเล็กน้อยของ x จะทำให้เกิดการเปลี่ยนแปลงเล็กน้อยใน y

จากการไล่ระดับ เราจะได้ข้อมูล 2 ข้อมูล ทิศทางที่พารามิเตอร์ต้องได้รับการปรับปรุง (เพิ่มขึ้นหรือลดลง) และเท่าใด (มากหรือน้อย)

กฎลูกโซ่

กฎลูกโซ่กล่าวอย่างไม่เป็นทางการว่า:

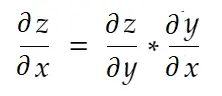
พิจารณาตัวอย่าง น้ำหนัก ด้านบน เราจำเป็นต้องคำนวณ grad_weight เพื่ออัปเดตน้ำหนักนี้ ซึ่งจะคำนวณโดย:

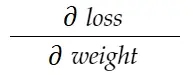
ด้วยสูตรกฎลูกโซ่ เราสามารถได้มันมา:

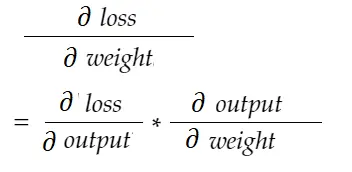
ในทำนองเดียวกันการไล่ระดับสีสำหรับอคติ:

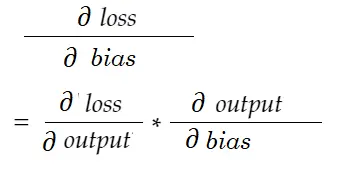
มาวาดแผนภาพการพึ่งพากัน

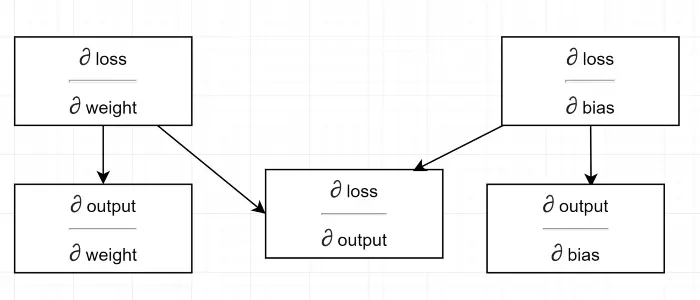
ดูการคำนวณทั้งหมดขึ้นอยู่กับการไล่ระดับของเอาต์พุต (∂ loss/∂ output) นั่นคือเหตุผลที่เราคำนวณมันก่อนบนแบ็คพาส (บรรทัด#34–36)

ที่จริงแล้ว ในเฟรมเวิร์ก ML ระดับสูง เช่น ใน PyTorch คุณไม่จำเป็นต้องเขียนโค้ดสำหรับแบ็คพาส! ในระหว่างการส่งต่อ จะสร้างกราฟการคำนวณ และในระหว่างการส่งผ่านกลับ จะส่งผ่านในทิศทางตรงกันข้ามในกราฟ และคำนวณการไล่ระดับสีโดยใช้กฎลูกโซ่

∂ สูญเสีย / ∂ ส่งออก

เรากำหนดตัวแปรนี้โดย grad_output ในโค้ด ซึ่งเราคำนวณในบรรทัด #34–36 มาหาเหตุผลเบื้องหลังสูตรที่เราใช้ในโค้ดกัน

จำไว้ว่าเรากำลังป้อนค่า 100 celsius_values ทั้งหมดในเครื่องด้วยกัน ดังนั้น grad_output จะเป็นอาร์เรย์ 100 องค์ประกอบ แต่ละองค์ประกอบมีการไล่ระดับสีของเอาต์พุตสำหรับองค์ประกอบที่เกี่ยวข้องใน celsius_values เพื่อความเรียบง่าย ให้เราพิจารณา มีเพียง 2 รายการใน celsius_values

ดังนั้น แบ่งบรรทัด #30

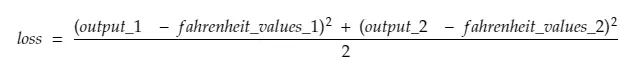
ที่ไหน,

output_1 = ค่าเอาต์พุตสำหรับค่า 1 เซลเซียส

output_2 = ค่าเอาต์พุตสำหรับค่าเซลเซียสที่ 2

fahreinheit_values_1 = ค่าฟาเรนไฮต์จริงสำหรับค่าเซลเซียสที่ 1

fahreinheit_values_1 = ค่าฟาเรนไฮต์จริงสำหรับค่าเซลเซียสที่ 2

ตอนนี้ ตัวแปรผลลัพธ์ grad_output จะมี 2 ค่า — gradient ของ output_1 และ output_2 ความหมาย:

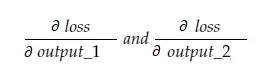
ให้เราคำนวณความชันของ output_1 เท่านั้น จากนั้นเราก็สามารถใช้กฎเดียวกันนี้กับกฎอื่นๆ ได้

เวลาแคลคูลัส!

ซึ่งเหมือนกับบรรทัด#34–36

ไล่น้ำหนัก

ลองนึกภาพ เรามีองค์ประกอบเดียวใน celsius_values ตอนนี้:

ซึ่งเหมือนกับบรรทัด#38–40 สำหรับ 100 celsius_values ค่าการไล่ระดับสีสำหรับแต่ละค่าจะถูกรวมเข้าด้วยกัน คำถามที่ชัดเจนก็คือ ทำไมเราไม่ลดขนาดผลลัพธ์ลง (เช่น หารด้วย SAMPLE_SIZE) เนื่องจากเรากำลังคูณการไล่ระดับสีทั้งหมดด้วยปัจจัยเล็กๆ ก่อนอัปเดตพารามิเตอร์ จึงไม่จำเป็น (ดูส่วนสุดท้าย การอัปเดตพารามิเตอร์)

อคติไล่ระดับ

ซึ่งเหมือนกับบรรทัด #42 เช่นเดียวกับการไล่ระดับน้ำหนัก ค่าเหล่านี้สำหรับอินพุต 100 รายการจะถูกรวมเข้าด้วยกัน อีกครั้ง เป็นเรื่องปกติเนื่องจากการไล่ระดับสีจะถูกคูณด้วยปัจจัยเล็กๆ ก่อนที่จะอัปเดตพารามิเตอร์

กำลังอัปเดตพารามิเตอร์

สุดท้ายนี้ เรากำลังอัปเดตพารามิเตอร์ โปรดสังเกตว่าการไล่ระดับสีคูณด้วยปัจจัยเล็กน้อย (LEARNING_RATE) ก่อนลบออก เพื่อให้การฝึกมีเสถียรภาพ ค่า LEARNING_RATE จำนวนมากจะทำให้เกิดปัญหาการ โอเวอร์โหลด และค่าที่น้อยมากจะทำให้การฝึกช้าลง ซึ่งอาจต้องทำซ้ำอีกมาก เราควรหาค่าที่เหมาะสมที่สุดด้วยการลองผิดลองถูก มีแหล่งข้อมูลออนไลน์มากมายรวมถึงแหล่งข้อมูลนี้เพื่อทราบข้อมูลเพิ่มเติมเกี่ยวกับอัตราการเรียนรู้

โปรดทราบว่าจำนวนเงินที่เราปรับนั้นไม่สำคัญอย่างยิ่ง ตัวอย่างเช่น หากคุณปรับ LEARNING_RATE เล็กน้อย ตัวแปร descent_grad_weight และ descent_grad_bias (บรรทัด#49–50) จะเปลี่ยนไป แต่เครื่องอาจยังทำงานอยู่ สิ่งสำคัญคือต้องแน่ใจว่าจำนวนเหล่านี้ได้มาจากการปรับขนาดการไล่ระดับสีด้วยปัจจัยเดียวกัน (LEARNING_RATE ในกรณีนี้) กล่าวอีกนัยหนึ่ง "การรักษาความลาดชันของการ ไล่ ระดับสีตามสัดส่วน" มีความสำคัญมากกว่า "การ ตกลง มามากแค่ไหน"

นอกจากนี้ ให้สังเกตด้วยว่าค่าการไล่ระดับสีเหล่านี้เป็นผลรวมของการไล่ระดับสีที่ประเมินสำหรับอินพุต 100 รายการแต่ละรายการ แต่เนื่องจากสิ่งเหล่านี้ถูกปรับมาตราส่วนด้วยค่าเดียวกัน จึงถือว่าใช้ได้ตามที่กล่าวไว้ข้างต้น

ในการอัพเดทพารามิเตอร์ เราต้องประกาศด้วยคำสำคัญสากล (ในบรรทัด#47)

จะไปไหนต่อจากนี้

โค้ดจะเล็กกว่ามากโดยแทนที่ for loops ด้วย list comprehension ด้วยวิธี pythonic ลองดูตอนนี้ — จะใช้เวลาไม่เกินสองสามนาทีเพื่อทำความเข้าใจ

หากคุณเข้าใจทุกอย่างจนถึงตอนนี้ อาจเป็นเวลาที่ดีที่จะเห็นเครือข่ายภายในแบบง่ายๆ ที่มีเซลล์ประสาท/เลเยอร์หลายชั้น นี่คือบทความ