การแจกแจงแบบปกติ – บทนำที่เข้าใจง่ายโดยไม่ต้องใช้คณิตศาสตร์

ฉันจะพยายามทำให้บทความนี้ปราศจากสมการและศัพท์เฉพาะ — ให้มากที่สุด อย่างไรก็ตาม ฉันต้องการให้คุณมีความสามารถดังต่อไปนี้เป็นอย่างน้อย:

• สามารถตีความกราฟอย่างง่ายได้
• ความรู้ระดับประถมศึกษาในเรื่องความน่าจะเป็น อย่างน้อยคุณเข้าใจดีว่ามีโอกาส 50% สำหรับหัวถ้าฉันโยนเหรียญ
• แคลคูลัสเชิงปริพันธ์และฟิสิกส์ควอนตัม (ล้อเล่น!)

ทำไมการกระจายแบบปกติ

วิธีที่เข้าใจง่ายในการทำความเข้าใจบางสิ่งคือการตรวจสอบว่าทำไมจึงจำเป็น ลองทำเพื่อการแจกแจงแบบปกติ (เรียกอีกอย่างว่าการกระจายแบบเกาส์เซียน)

สมมติว่าคุณมีนิสัยที่ตลก ทุกวันคุณโยนเหรียญ 100 ครั้ง เป็นเรื่องปกติที่จะคาดหวังว่าคุณจะได้รับศีรษะ 50 ครั้ง - หรือเกือบ 50 ครั้งเกือบทุกวัน ไม่ค่อยมีวันที่ดีสำหรับศีรษะ คุณอาจได้รับประมาณ 55 ครั้ง และแทบจะไม่เกิน 65 ครั้งมากนัก

ตอนนี้ คุณต้องการหาปริมาณ "ความหายาก" นี้ ดังนั้นคุณเริ่มติดตามจำนวนครั้งที่คุณได้รับหัวทุกวัน

จำนวนหัวทุกวันในหนึ่งปี

ด้านล่างนี้คือข้อมูลหลังจากหนึ่งปี (365 วัน) — อันแรกคือจำนวนหัวที่คุณได้รับในวันแรก และอันสุดท้ายคือจำนวนหัวที่คุณได้รับในวันสุดท้าย คุณไม่จำเป็นต้องตรวจสอบตัวเลขทั้งหมดด้านล่าง แต่สังเกตได้ง่ายว่าตัวเลขส่วนใหญ่อยู่ที่ประมาณ 50

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

แสดงภาพได้ดีขึ้นด้วยฮิสโตแกรม

ลองพล็อตฮิสโตแกรมจากข้อมูลด้านบนกัน:

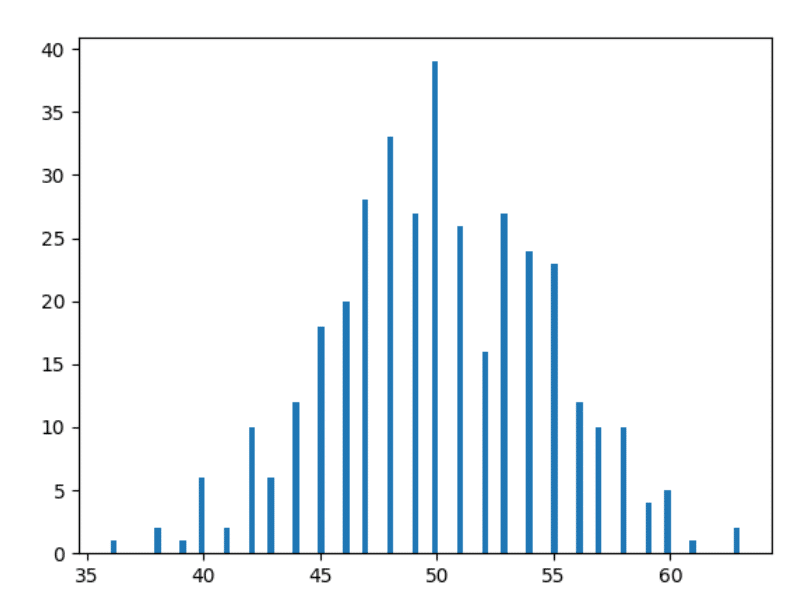
อ้า! มันดูไม่เหมือนภาพที่คุณเห็นบนอินเทอร์เน็ตเมื่อคุณค้นหาคำว่า "Normal Distribution" ใช่หรือไม่? เราเกือบจะอยู่ที่นั่นแล้ว!

ดังนั้น หากคุณไม่เข้าใจฮิสโตแกรม เราเพิ่งพล็อตมานับจำนวนวันที่เรานับหัวโดยเฉพาะ ตัวอย่างเช่น เราได้หัว 36 ครั้งใน 2 วันโดยเฉพาะอย่างยิ่งในปี (ตรวจสอบข้อมูลด้านบนหากคุณไม่เชื่อฉัน) นั่นเป็นสาเหตุที่มีแถบความสูง 2 หน่วยบนจุดแนวนอนที่ 36 (สีแดง สี่เหลี่ยมด้านซ้ายในภาพด้านล่าง)

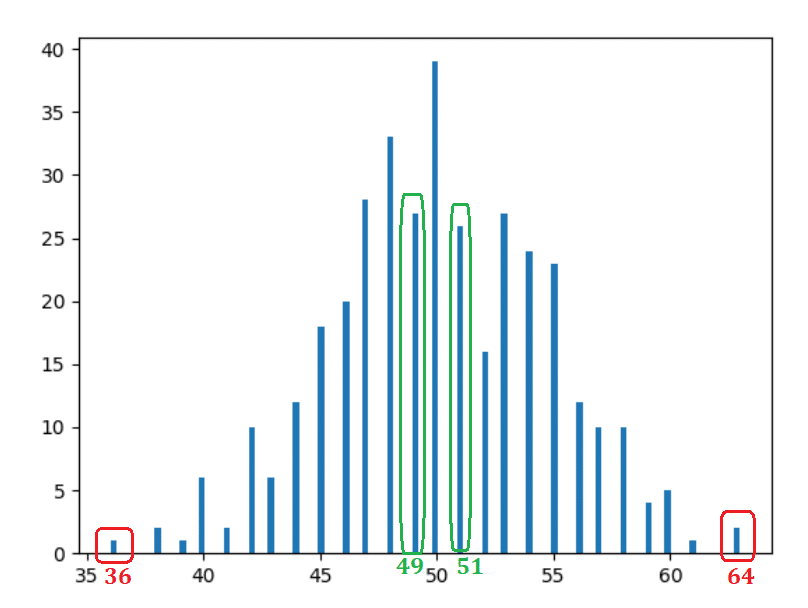
ข้อสังเกต

1. ค่อนข้างชัดเจนและคาดหวัง - 50 หัวเกิดขึ้นเกือบทุกครั้ง
2. ยิ่งเราออกจากศูนย์กลาง (50) มากเท่าไร เหตุการณ์ก็ลดลงเป็นส่วนใหญ่
3. แท่งที่ระยะห่างเท่ากันมีรูปร่างคล้ายกัน ตัวอย่างเช่น หากคุณย้ายหนึ่งหน่วยไปทางซ้าย (49) หรือทางขวา (51) เหตุการณ์จะคล้ายกัน — 30 และ 31 ตามลำดับ (สี่เหลี่ยมสีเขียว) หากคุณย้าย 14 หน่วยไปทางซ้าย (36) หรือขวา (64) เหตุการณ์จะคล้ายกันอีกครั้ง — 2 และ 1 ตามลำดับ (สี่เหลี่ยมสีแดง)

ข้อมูล 10 ปี

ทีนี้มาต่อกันอย่างรวดเร็ว — และพล็อตข้อมูล 10 ปี

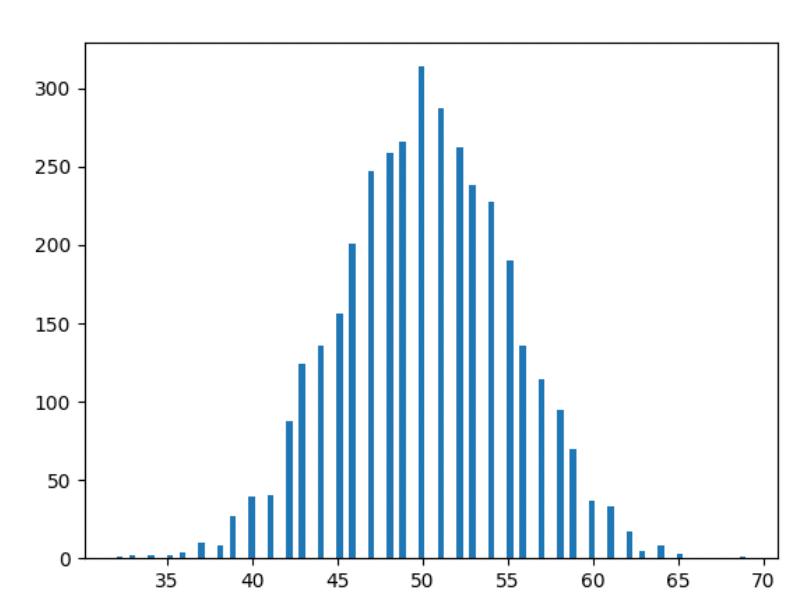
ข้อมูล 1,000 ปี

โอเค - คนสุดท้าย ลองพลอตข้อมูล 1,000 ปีกัน

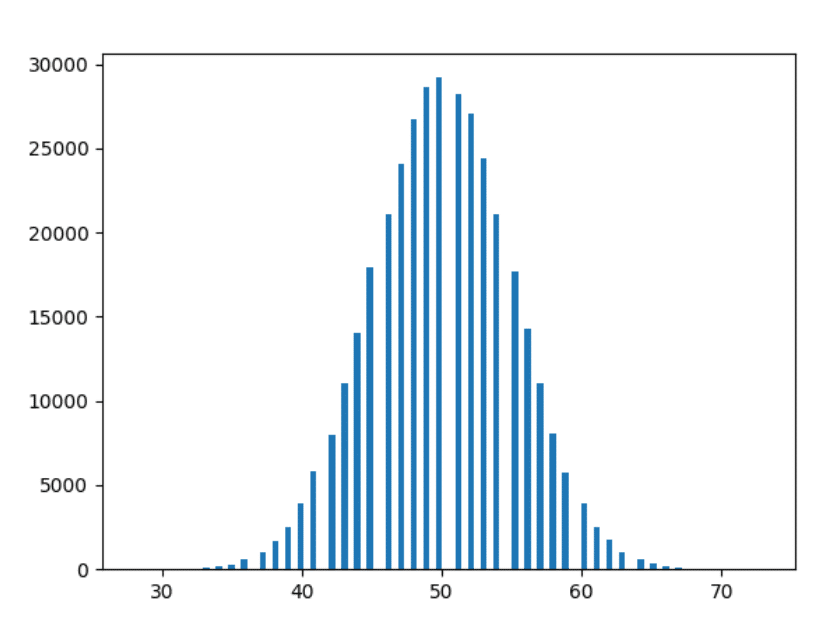
ข้อสังเกต

1. ยิ่งเราทดลองมากเท่าไหร่ รูปร่างก็จะยิ่งเรียบเนียนขึ้นเท่านั้น
2. ยิ่งเราทดลองมากเท่าไร แท่งแท่งต่างๆ จะยิ่งติดตามการสังเกตด้านบนมากขึ้นเท่านั้น (เช่น แท่งที่ระยะห่างใกล้เคียงกันจะมีรูปร่างที่ใกล้เคียงกันมากขึ้น)

การแจกแจงแบบปกตินั้นอยู่ที่ไหน

เอาล่ะ - พื้นหลังมากเกินไป - ตอนนี้มาที่ประเด็นกัน

มาดูคำตอบที่แนะนำโดย Google:

บางสิ่งในคำจำกัดความนี้:

ตัวแปรสุ่ม: พูดง่ายๆ ก็คือ ตัวแปรสุ่มคือชุดของค่าที่เป็นไปได้ของการทดลองแบบสุ่ม เช่น การโยนเหรียญ ในตัวอย่างของเรา ค่าที่เป็นไปได้ของการทดสอบของเราคือ Head หรือ Tail

รูประฆัง: คุณสังเกตเห็นไหมว่าฮิสโทแกรมของเราเป็นรูประฆัง?

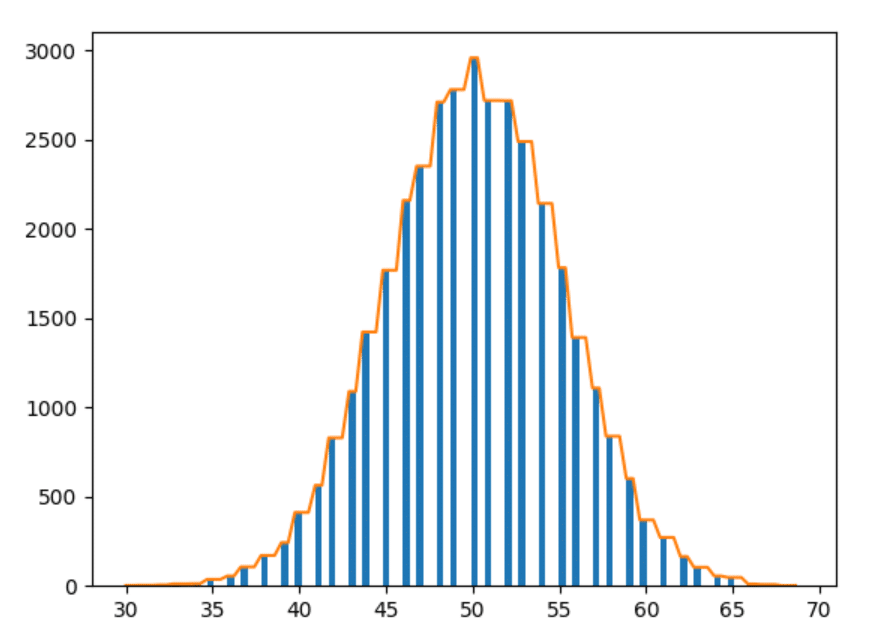
สมมาตร: แท่งที่ระยะห่างเท่ากันมีรูปร่างคล้ายกัน — ไม่สมมาตรใช่หรือไม่

ดังนั้น การแจกแจงแบบปกติหมายถึงการแจกแจงผลลัพธ์สำหรับเหตุการณ์ เช่น การโยนเหรียญ ซึ่งการแจกแจงมีแนวโน้มที่จะรักษาคุณสมบัติบางอย่างไว้ รวมถึงความสมมาตรและรูปทรงระฆัง

ปรากฏการณ์ใดนอกจากการโยนเหรียญตามการแจกแจงแบบปกติ

ตัวอย่างเด็ด ๆ ที่นี่

• ความสูงของประชากร — ผู้คนจำนวนมากขึ้นตกอยู่ในกลุ่มความสูงเฉลี่ย หายากมากที่จะพบคนที่สูงมากหรือเตี้ยมาก และโอกาสที่จะพบความสูงมากและสั้นมากนั้นเกือบจะเท่ากัน
• ทอยลูกเต๋า
• ขนาดรองเท้า
• ไอคิว
• และอื่นๆ อีกมาก…

ปรากฏการณ์เหล่านี้ปฏิบัติตามการแจกแจงแบบปกติอย่างเคร่งครัดหรือไม่?

คำตอบง่ายๆคือไม่ แม้ว่าดังที่เราเห็นข้างต้น ยิ่งคุณทำการทดสอบมากเท่าใด ข้อมูลก็จะยิ่งเป็นไปตามคุณสมบัติการกระจายแบบปกติมากขึ้นเท่านั้น แต่ไม่มีการรับประกันว่าเหตุการณ์ที่ไม่น่าจะเกิดขึ้นบางอย่างจะไม่เกิดขึ้นอยู่ดี

การแจกแจงความน่าจะเป็นทั้งหมดในจักรวาลเป็นการแจกแจงแบบปกติหรือไม่?

ไม่ มีปรากฏการณ์มากมายที่กำหนดโดยการกระจายแบบอื่น

• ความน่าจะเป็นของลูกค้าจำนวนหนึ่งที่จะมาถึง การโทรศัพท์ อุบัติเหตุ การแข่งขันกีฬา และน้ำท่วม เป็นไปตาม การกระจายของปัวซอง
• สำหรับการขายเชิงธุรกิจ ลูกค้าของบริษัท 20% รับผิดชอบยอดขาย 80% ( จำหน่ายพาเรโต้ )
• รูปแบบการจราจรในเมือง — การกระจายแบบทวีคูณ
• สุ่มเลือกสมาชิกสำหรับทีมจากประชากรของเด็กหญิงและเด็กชาย — Hypergeometric Distribution

และอื่น ๆ อีกมากมาย …

ฉันสร้างรายการข้างต้นโดยเพียงแค่ googling "ตัวอย่างชีวิตจริง" พร้อมการแจกแจงบางส่วนที่แสดงไว้ที่นี่ ไม่ใช่ว่าฉันเข้าใจทั้งหมด 😉

มีเหตุผลว่าทำไมปรากฏการณ์ทางธรรมชาติบางอย่างจึงมีแนวโน้มที่จะติดตามการแจกแจงแบบปกติ

ใช่ — ยกคำอธิบายที่ฉันชอบ:

คำอธิบายทั่วไปมีให้โดยชื่ออื่นสำหรับการแจกแจงแบบปกติ ซึ่งก็คือ "การกระจายข้อผิดพลาด" แนวคิดก็คือข้อผิดพลาดโดยทั่วไปมักเกิดขึ้นแบบสุ่ม ดังนั้น จึงมีแนวโน้มที่จะไปในทิศทางเดียวเช่นเดียวกับในอีกทางหนึ่ง ตัวอย่างเช่น นักแม่นปืนมักจะยิงไปทางซ้ายเล็กน้อย ไปทางขวาเล็กน้อย หรือสูงแต่ต่ำเล็กน้อย ดังนั้น กราฟของระยะที่ช็อตจากเป้าจะสะท้อนถึงแนวโน้มแบบสุ่มนี้ และมีความสมมาตรรอบๆ ค่าเฉลี่ย ในทำนองเดียวกัน ด้วยความสูงและสติปัญญา ยีนจำนวนมาก (อาจเป็นหลายพัน) มีส่วนทำให้เกิดผลลัพธ์เหล่านี้ เช่นเดียวกับปัจจัยแวดล้อมจำนวนมาก เช่น โภชนาการ การเจ็บป่วย รายได้ต่ำ และอื่นๆ

พารามิเตอร์ของการแจกแจงแบบปกติ

หากคุณมีสัญชาตญาณของการสนทนาจนถึงตอนนี้ แสดงว่าคุณเป็นผู้ชนะแล้ว ภารกิจเสร็จสมบูรณ์. ส่วนที่เหลือของบทความเป็นโบนัส

กราฟการแจกแจงแบบปกติทั้งหมดที่คุณเห็นมีรูปร่างต่างกัน บางคนก็ประจบประแจงกว่าคนอื่น ๆ บางคนมีความสูงที่ดี รูปร่างทั้งหมดเหล่านี้ถูกควบคุมโดยพารามิเตอร์ 2 ตัวเท่านั้น:

หมายถึง

ค่าเฉลี่ยถูกกำหนดโดยค่าเฉลี่ย มันกำหนดความสูงของระฆัง สำหรับตัวอย่างการโยนเหรียญ ค่าเฉลี่ยอยู่ใกล้ 50 ซึ่งเป็นตำแหน่งบนสุดในกราฟ

ส่วนเบี่ยงเบนมาตรฐาน

เนื่องจากฉันสัญญาว่าบทความนี้จะปราศจากสมการ ฉันจึงไม่แสดงการแทนค่าทางคณิตศาสตร์ที่นี่ แต่มันก็ไม่ได้ยากอยู่ดี ส่วนเบี่ยงเบนมาตรฐานคือตัวชี้วัดที่แสดงถึงความหลากหลายของข้อมูล

ตัวอย่างเช่น ค่าเบี่ยงเบนมาตรฐานของอายุในการดูแลเด็กจะต่ำกว่าค่าเบี่ยงเบนมาตรฐานของอายุในแฟนคลับฟุตบอล เนื่องจากช่องว่างอายุระหว่างกลุ่มที่อายุน้อยที่สุดและแก่ที่สุดควรสูงกว่ามากในแฟนคลับฟุตบอล

ส่วนเบี่ยงเบนมาตรฐานกำหนดความกว้างของเส้นโค้ง ส่วนเบี่ยงเบนมาตรฐานขนาดเล็กทำให้เกิดเส้นโค้งที่สูงชัน และค่าเบี่ยงเบนมาตรฐานที่ใหญ่กว่าจะสร้างเส้นโค้งที่แบนราบกว่า