สัมผัสแคลคูลัสด้วยความรู้สึกในการเขียนโปรแกรมของคุณ

ฉันเชื่อว่าคนที่เขียนโค้ดได้ — มีความสามารถในการเข้าใจแนวคิดที่ซับซ้อนกว่าแคลคูลัส เหตุผลหนึ่งที่ว่าทำไมมีโปรแกรมเมอร์ที่มีความสามารถจำนวนมากที่ยังมีปัญหากับแคลคูลัสอยู่นั้นไม่ได้ยากเลย ส่วนใหญ่เป็นเพราะเราถูกสอนมาในทางที่ผิด (พร้อมกับหัวข้ออื่นๆ อีกมากมาย)

หากคุณเคยเขียนโค้ดมาในชีวิตแล้ว แม้แต่แบบฝึกหัดของเล่น เช่น การสร้างจำนวนเฉพาะ คุณอาจเคยทำสิ่งที่คล้ายกันซึ่งเกิดขึ้นในแคลคูลัสแต่ไม่มีโอกาสได้มีส่วนร่วม

วัตถุประสงค์ของการเขียนนี้ไม่ใช่เพื่อสอนแคลคูลัสหรือการเขียนโปรแกรม แต่เพื่อช่วยให้คุณเชื่อมโยงบางจุด

ฉันจะไปที่ส่วนการเข้ารหัสในไม่กี่นาที แต่ขอเล่าเบื้องหลังคร่าวๆ ก่อนว่า

อัตราการเปลี่ยนแปลง

แคลคูลัสเชิงอนุพันธ์พูดถึง "อัตราการเปลี่ยนแปลง" ลองทำความเข้าใจว่าหมายถึงอะไร

สำหรับการเปลี่ยนแปลงในตัวแปร (x) อัตราการเปลี่ยนแปลงของฟังก์ชันเป็นเพียงการเปลี่ยนแปลงในฟังก์ชันหารด้วยการเปลี่ยนแปลงใน x ให้เห็นภาพด้วยตัวเลขจริง:

พิจารณา 2 จุด x=2 และ x=6 และฟังก์ชัน y=f(x) = x²

นอกจากนี้ ให้พิจารณา dx = ระยะห่างระหว่าง 2 จุดเหล่านี้ในแกน x และ dy คือระยะห่างระหว่างค่า y สำหรับค่า x เหล่านี้

จากนั้น อัตราการเปลี่ยนแปลงของ y จาก x=2 ถึง x=6 is

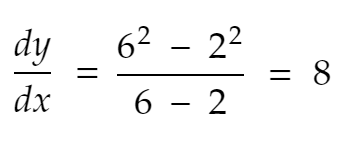
อนุพันธ์

ทีนี้ — อนุพันธ์ dy/dx คืออัตราการเปลี่ยนแปลงของ y สำหรับการเปลี่ยนแปลงเพียงเล็กน้อยใน x เนื่องจากระยะทางนี้ (6–2=4) ไม่ได้เล็กมาก — ไม่ใกล้เลย เราจึงเรียกสมการข้างบนนี้ว่าอนุพันธ์ไม่ได้ ลองเลือกจำนวนที่น้อยกว่า 0.1 ตอนนี้

เมื่อ x = 0, y = x² = 0² = 0

เพื่อนบ้านที่ใกล้ที่สุดกับทิศทางบวก x = 0.1 โดยที่ y กลายเป็น 0.1² = 0.01

ดังนั้น,

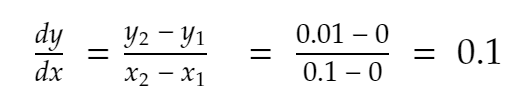
มาลองกันอีกครั้ง เพื่อนบ้านที่ใกล้ที่สุดของ 0.1 ไปยังทิศทางบวก x = 0.2 ดังนั้น y กลายเป็น 0.2² = 0.04 ดังนั้น,

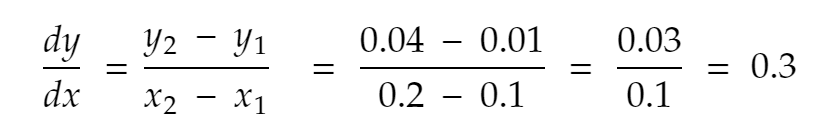
หากเราทำซ้ำอีกสองสามครั้ง นี่คือสิ่งที่เราได้รับ:

นี่คือไฟล์ excel หากคุณต้องการเล่นกับมัน

dx (ซึ่งเป็นระยะห่างเล็กน้อยในจินตนาการของเราระหว่างจุดที่อยู่ติดกัน 2 จุดบนแกน x) คือ 0.1 ในบริบทของเรา

x เพิ่มขึ้นตามลำดับ

y ก็แค่ x²

dy คือระยะห่างระหว่างค่า y 2 ค่าที่อยู่ติดกัน ตัวอย่างเช่น เมื่อ x= 0.1 ระยะห่างระหว่างกระแส y (0.01 ) และ y ถัดไป (0.04) คือ 0.03 ดังนั้น dy คือ 0.03 ที่ x=0.1

dy/dx คือ dy หารด้วย dx

dy/dx / x คือ dy/dx หารด้วย x

สังเกตว่า เมื่อ x เพิ่มขึ้น แถวสุดท้ายจะเข้าใกล้ 2 ซึ่งหมายความว่า — อัตราการเปลี่ยนแปลงของ x² เทียบกับ x กำลังเข้าใกล้สองเท่าของ x ซึ่งเท่ากับ 2x

จำอนุพันธ์ของ x² เทียบกับ x ได้ไหม 2x! กำลังหาการเชื่อมต่อ?

เวลาเข้ารหัส

มาลองทำสิ่งต่าง ๆ ในโค้ดที่เราได้พูดคุยกันถึงตอนนี้

สมมติว่าคุณติดตั้ง Python ไว้แล้วในเทอร์มินัล ให้รัน:

หลังจากนั้นให้รันโค้ด Python ต่อไปนี้:

ที่นี่:

x : มีตัวเลขตั้งแต่ 0 ถึง 9

y : อาร์เรย์อื่น แต่ละองค์ประกอบเป็นกำลังสองขององค์ประกอบ x ที่สอดคล้องกัน

dy : อาร์เรย์อื่นเริ่มต้นด้วยศูนย์ เราจะใส่ระยะ y ในอาร์เรย์นี้

dydx : อาร์เรย์อื่นเริ่มต้นด้วยศูนย์ มันจะมีค่า dy/dx ของทุกจุด

dx : ค่อนข้างชัดเจน — มันคือขนาดขั้นตอน ระยะห่างระหว่างตัวเลข 2 ตัวติดต่อกัน ซึ่งจะลดลงเมื่อ SIZE เพิ่มขึ้น ถ้าขนาด = 10 dx = 1 ถ้าขนาด = 100 dx = 0.1

อันดับแรก เราได้รับ dy ทุกจุด จากนั้นเราคำนวณ dydx จากมัน

สังเกตว่า:

ที่นี่เรากำลังละเว้นค่าแรกและค่าสุดท้าย ค่าแรกของ x คือ 0 ซึ่งจะทำให้เกิดข้อผิดพลาดในการแบ่งศูนย์ และเราไม่สามารถคำนวณค่าสุดท้ายของ dy/dx ได้ เนื่องจากเราไม่มีค่าสุดท้ายของ dy — เพราะมันต้องการถัดจากค่าที่มีสุดท้ายของ y ซึ่งเราไม่มีที่นี่

หากทุกอย่างเป็นไปด้วยดี คุณจะได้กราฟนี้:

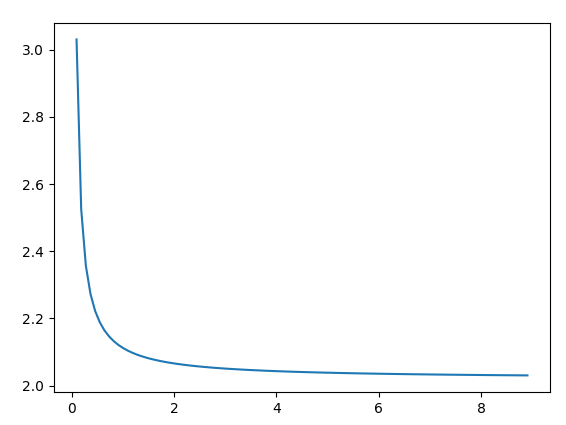
สิ่งที่คุณเข้าใจจากโครงเรื่อง

อย่างที่คุณเห็น กราฟกำลังเข้าใกล้ 2 เพิ่มค่าของ SIZE (หมายถึงการตั้งค่าต่ำกว่า dx) และดูว่ากราฟเข้าใกล้ 2 เร็วขึ้นได้อย่างไร

อนุพันธ์อันดับสอง

ตอนนี้คุณมาไกลถึงขนาดนี้แล้ว อีกไม่กี่ขั้นตอนเพื่อทำความเข้าใจอนุพันธ์อันดับสอง ซึ่งจะทำให้คุณได้สัญชาตญาณสำหรับอนุพันธ์ของคำสั่งใดๆ

อย่างที่คุณจำได้ อนุพันธ์อันดับสองคืออัตราการเปลี่ยนแปลงของอนุพันธ์อันดับหนึ่งเทียบกับ x พูดง่ายๆ — dy/dx ในอนุพันธ์อันดับสองก็เหมือน y ในอนุพันธ์อันดับหนึ่ง

มาทำการแก้ไขต่อไปนี้กับโค้ดด้านบน:

ประกาศ 2 อาร์เรย์เพิ่มเติม:

d2ydx2 : ซึ่งจะเป็นตัวแทนของอนุพันธ์อันดับสอง:

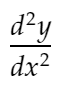
Distance_dydx: เพื่อแสดงระยะห่างระหว่างค่า dy/dx ระหว่าง 2 จุดที่อยู่ติดกัน

นี่คือรหัสเต็มสำหรับอนุพันธ์อันดับสอง:

หลังจากคำนวณ dydx ในลูป for แล้ว เราจะรันลูปอื่นเพื่อคำนวณอนุพันธ์อันดับสอง ด้วยการเข้ารหัสที่ชาญฉลาด เราสามารถคำนวณอนุพันธ์อันดับสองในวงเดียวกัน (ลองทำแบบฝึกหัด) — แต่ฉันแยกมันไว้ที่นี่เพื่อความชัดเจน

นอกจากนี้ ให้สังเกตว่า:

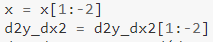
อย่างที่เราทำในอนุพันธ์อันดับ 1 เรากำลังละเว้นค่าบางค่าที่นี่ด้วย ค่า 2 ค่าสุดท้ายจะถูกละเว้นเนื่องจากค่าที่สองจากค่าสุดท้ายจะต้องใช้ค่า "อนุพันธ์อันดับแรก" ล่าสุด ซึ่งเราไม่สามารถคำนวณได้ (เนื่องจากเราไม่มีค่า y ที่จำเป็นสำหรับค่าดังกล่าว — ตามที่อธิบายข้างต้น) หมายความว่าเราต้องละเว้น 3 ค่าสุดท้ายในกรณีของอนุพันธ์อันดับ 3 หรือไม่🤔 — นั่นคือให้คุณค้นหา

นี่คือกราฟผลลัพธ์:

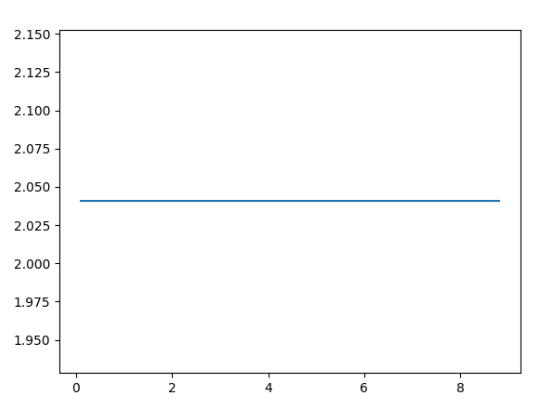
เราเห็นอะไรที่นี่?

อย่างที่คุณรู้จากโรงเรียนมัธยม:

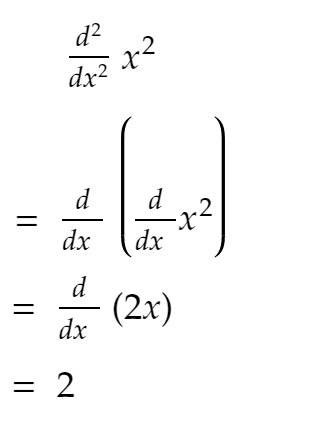
อย่างที่คุณเห็นจากโค้ดด้านบน อนุพันธ์อันดับสองส่วนใหญ่คงที่ และถ้าคุณเพิ่ม SIZE ไปเรื่อย ๆ มันจะเข้าใกล้ 2!

ทำไมอัตราการเปลี่ยนแปลงจึงสำคัญ

คุณอาจสงสัยว่า:

— ทำไมเราถึงผ่านปัญหาที่น่ารังเกียจเหล่านี้ทั้งหมด? เราได้ข้อมูลที่เป็นประโยชน์อะไรบ้างจากอัตราการเปลี่ยนแปลงหรืออนุพันธ์?

— ทำไมเราไม่สามารถไปกับอัตราการเปลี่ยนแปลงสำหรับจำนวนเท่าใดก็ได้? ทำไมจึงเล็กนิดเดียว? เราได้รับข้อมูลอะไรบ้างจากอัตราการเปลี่ยนแปลงเมื่อเทียบกับ ค่าขนาดเล็กที่ไม่สิ้นสุด ซึ่งไม่สามารถหาได้จากอัตราการเปลี่ยนแปลงเมื่อเทียบกับค่าที่มากกว่า

— สิ่ง เล็ก ๆ น้อย ๆ นี้ดูเหมือนแฮ็ค? เราทำงานกับตัวเลขเล็กๆ ด้านบนนี้ แต่แน่นอนว่าไม่ใช่จำนวนที่น้อยมาก

ถ้าฉันยอมให้ไปต่อ เธอคงเดินจากไปเห็นความยาวของบทความนี้ และคงไม่มาไกลถึงขนาดนี้ บางทีเราจะตอบคำถามเหล่านั้นในวันอื่น😀