สถิติแบบเบย์: ไพรเมอร์ที่รวดเร็วและปราศจากโฆษณาเกินจริงของผู้ทดสอบ A/B
เผยแพร่แล้ว: 2022-06-23
คุณมั่นใจในความสามารถในการตีความผลลัพธ์ที่ได้จากเครื่องมือทดสอบ A/B ของคุณมากน้อยเพียงใด
สมมติว่าคุณกำลังใช้เครื่องมือที่สร้างขึ้นจากสถิติแบบเบย์ และมันบอกคุณว่า “B” มีโอกาส 70% ที่จะเอาชนะ “A” ดังนั้น “B” จึงเป็นผู้ชนะ คุณรู้หรือไม่ว่ามันหมายถึงอะไรและควรแจ้งกลยุทธ์ CRO ของคุณอย่างไร?
ในบทความนี้ คุณจะได้เรียนรู้พื้นฐานของสถิติแบบเบย์ที่จะช่วยให้คุณกลับมาควบคุมการทดสอบ A/B ของคุณได้ ซึ่งรวมถึง
- มุมมองที่ เป็นกลาง ของสถิติแบบเบย์
- Frequentist vs Bayesian ข้อดีและข้อเสีย
- การเตรียมการที่คุณต้องตีความและใช้ผลการทดสอบ A/B แบบเบย์อย่างมั่นใจ ในขณะที่หลีกเลี่ยงกับดักในตำนานทั่วไป
- สถิติแบบเบย์คืออะไร?
- เรื่องราวต้นกำเนิดแบบเบย์
- ตัวอย่างสถิติเบย์ที่ใช้กับการทดสอบ A/B
- อภิธานศัพท์สั้นๆ ของคำศัพท์ Bayesian ที่มีความสำคัญต่อผู้ทดสอบ A/B
- การอนุมานแบบเบย์
- ความน่าจะเป็นแบบมีเงื่อนไข
- การกระจายความน่าจะเป็น/การกระจายความน่าจะเป็น
- การกระจายความเชื่อก่อนหน้า
- คอนจูกาซี
- Conjugate Priors
- ฟังก์ชั่นการสูญเสีย
- สถิติความถี่คืออะไร?
- การทดสอบ A/B แบบ Bayesian กับ Frequentist
- กรอบงานบ่อย
- กรอบการทำงานแบบเบย์
- สถิติแบบเบย์บอกอะไรคุณได้บ้างในการทดสอบ A/B?
- ความน่าจะเป็นที่จะดีที่สุด (P2BB)
- ความคาดหวังที่เพิ่มขึ้น
- ขาดทุนที่คาดหวัง
- ตำนานเกี่ยวกับสถิติแบบเบย์ที่ควรหลีกเลี่ยง
- ตำนาน # 1: Bayesians ระบุสมมติฐานของพวกเขา Frequentists Don't
- ตำนาน # 2 วิธีการแบบเบย์ให้คำตอบที่คุณต้องการจริงๆ
- ตำนาน #3: การอนุมานแบบเบย์ช่วยให้คุณสื่อสารความไม่แน่นอนได้ดีกว่าการอนุมานบ่อยๆ
- ตำนาน #4. ผลการทดสอบ A/B ของ Bayesian มีภูมิคุ้มกันต่อการแอบมอง
- ตำนาน #5. สถิติที่ใช้บ่อยนั้นไม่มีประสิทธิภาพเนื่องจากคุณต้องรอขนาดตัวอย่างคงที่
- ดังนั้นคุณควรเลือก Bayesian หรือ Frequentist หรือไม่? มีที่สำหรับทั้งคู่
- ที่สำคัญ Takeaway
พร้อม? เริ่มจากพื้นฐานกันก่อน
สถิติแบบเบย์คืออะไร?
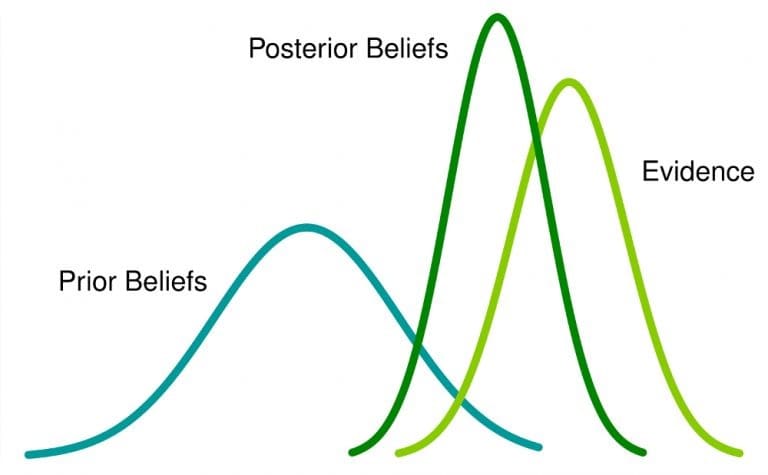
สถิติแบบเบย์เป็นวิธีการวิเคราะห์ทางสถิติที่อิงตามทฤษฎีบทของเบย์ ซึ่งอัปเดตความเชื่อเกี่ยวกับเหตุการณ์เมื่อมีการรวบรวมข้อมูลใหม่หรือหลักฐานเกี่ยวกับเหตุการณ์เหล่านั้น ในที่นี้ ความน่าจะเป็นเป็นหน่วยวัดความเชื่อที่ว่าเหตุการณ์หนึ่งเกิดขึ้น
สิ่งนี้หมายความว่า: หากคุณมีความเชื่อมา ก่อน เกี่ยวกับเหตุการณ์ และได้รับข้อมูลเพิ่มเติมเกี่ยวกับเหตุการณ์นั้น ความเชื่อนั้นจะเปลี่ยนแปลง (หรืออย่างน้อยก็ถูกปรับ) เป็นความเชื่อใน ภายหลัง
สิ่งนี้มีประโยชน์สำหรับการทำความเข้าใจความไม่แน่นอนหรือเมื่อทำงานกับข้อมูลที่มีเสียงรบกวนมากมาย เช่น ในการเพิ่มประสิทธิภาพอัตรา Conversion สำหรับอีคอมเมิร์ซและในการเรียนรู้ของเครื่อง
ลองนึกภาพสิ่งนี้:
ตัวอย่างเช่น สมมติว่าคุณกำลังดูการแข่งขันรถเข็นขายของในมหาวิทยาลัย จากนั้นผู้ชมที่ตื่นเต้นท้าให้คุณเดิมพันว่าผู้ชายที่ใส่เสื้อยืดสีแดงลากผู้หญิงที่ใส่เสื้อสีเขียวจะเป็นผู้ชนะ ลองคิดดูและโต้กลับว่าชายเสื้อดำและสาวเสื้อฮู้ดดำจะชนะแทน

ผู้ชมอีกคนอยู่เหนือศีรษะและกระซิบเคล็ดลับกับคุณว่า “ชายเสื้อแดงชนะการแข่งขัน 3 รายการสุดท้ายจาก 4 รายการ” จะเกิดอะไรขึ้นกับการเดิมพันของคุณ? คุณไม่แน่ใจอีกต่อไปแล้วใช่ไหม
สมมติว่าคุณได้เรียนรู้ด้วยว่าครั้งสุดท้ายที่ชายแจ็กเก็ตสีดำสวมแว่นกันแดดนำโชคของเขา เขาชนะ และครั้งที่เขาไม่ใส่มัน คนเสื้อแดงก็ชนะ
วันนี้คุณเห็นชายแจ็กเก็ตสีดำสวมแว่นตานั่น ความเชื่อของคุณเปลี่ยนไปอีกครั้ง ตอนนี้คุณมีความเชื่อมั่นในการเดิมพันของคุณมากขึ้นใช่ไหม ในเรื่องนี้ คุณได้อัปเดตความเชื่อของคุณทุกครั้งที่มีหลักฐานของข้อมูลใหม่ นั่นคือแนวทางแบบเบย์เซียน
เรื่องราวต้นกำเนิดแบบเบย์
เมื่อสาธุคุณโธมัส เบย์สนึกถึงทฤษฎีของเขาเป็นครั้งแรก เขาไม่คิดว่ามันควรค่าแก่การตีพิมพ์ ดังนั้นมันจึงอยู่ในบันทึกของเขามานานกว่าทศวรรษ เมื่อครอบครัวของเขาขอให้ริชาร์ด ไพรซ์อ่านบันทึกของเขาว่าไพรซ์ค้นพบโน้ตที่เป็นรากฐานของทฤษฎีบทของเบย์
มันเริ่มต้นด้วยการทดลองทางความคิดของเบย์ เขาคิดที่จะนั่งโดยให้หลังของเขากับโต๊ะแบนราบและให้ผู้ช่วยโยนลูกบอลลงบนโต๊ะ
ลูกบอลสามารถตกลงไปที่ใดก็ได้บนโต๊ะ แต่ Bayes คิดว่าเขาสามารถเดาได้ว่าที่ไหนโดยอัปเดตการเดาของเขาด้วยข้อมูลใหม่ เมื่อลูกบอลตกลงบนโต๊ะ ให้ผู้ช่วยบอกเขาว่าลูกบอลตกลงไปทางซ้ายหรือขวา ข้างหน้าหรือข้างหลัง
เขาตั้งข้อสังเกตและฟังเมื่อลูกบอลตกลงบนโต๊ะมากขึ้น ด้วยข้อมูลเพิ่มเติมเช่นนี้ เขาพบว่าเขาสามารถปรับปรุงความแม่นยำในการเดาของเขาได้ในการโยนแต่ละครั้ง สิ่งนี้ทำให้เกิดแนวคิดในการปรับปรุงความเข้าใจของเราในขณะที่เราได้รับหลักฐานเพิ่มเติมจากการสังเกต
แนวทาง Bayesian ในการวิเคราะห์ข้อมูลถูกนำไปใช้ในหลายสาขา เช่น วิทยาศาสตร์และวิศวกรรมศาสตร์ และรวมถึงกีฬาและกฎหมายด้วย
ในการทดลองควบคุมแบบสุ่มทางออนไลน์ โดยเฉพาะการทดสอบ A/B คุณสามารถใช้แนวทางแบบเบย์ใน 4 ขั้นตอน:
- ระบุการแจกจ่ายก่อนหน้าของคุณ
- เลือกแบบจำลองทางสถิติที่สะท้อนความเชื่อของคุณ
- เรียกใช้การทดสอบ
- หลังจากการสังเกต ปรับปรุงความเชื่อของคุณและคำนวณการแจกแจงหลัง
คุณอัปเดตความเชื่อของคุณโดยใช้ชุดกฎที่เรียกว่าอัลกอริทึมแบบเบย์
ตัวอย่างสถิติเบย์ที่ใช้กับการทดสอบ A/B
มาดูตัวอย่างการทดสอบ A/B แบบเบย์กัน
ลองนึกภาพว่าเราทำการทดสอบ A/B แบบง่ายๆ บนปุ่ม CTA ของร้านค้า Shopify สำหรับ “A” เราใช้ “Add to Cart” และสำหรับ “B” เราใช้ “Add to Your Basket”
นี่คือวิธีที่ผู้ที่มาบ่อยจะเข้าใกล้การทดสอบ
มีสองโลกทางเลือก: โลกหนึ่งที่ A และ B ไม่แตกต่างกัน ดังนั้นการทดสอบจะไม่แสดงความแตกต่างของอัตราการแปลง นั่นคือสมมติฐานว่าง และในอีกโลกหนึ่ง มีความแตกต่างกัน ดังนั้นปุ่มหนึ่งจะทำงานได้ดีกว่าอีกปุ่มหนึ่ง
ผู้ที่ใช้บ่อยจะถือว่าเราอยู่ในโลกที่ 1 ซึ่งไม่มีความแตกต่างในปุ่ม CTA นั่นคือ สมมติว่าสมมติฐานว่างเป็นจริง จากนั้นพวกเขาจะพยายามพิสูจน์ว่าผิดถึงระดับความแน่นอนที่กำหนดไว้ล่วงหน้าซึ่งเรียกว่าระดับนัยสำคัญ
แต่นี่คือวิธีที่ Bayesian จะทำการทดสอบแบบเดียวกัน:
พวกเขาเริ่มต้นด้วยความเชื่อก่อนหน้านี้ว่าทั้งปุ่ม A และ B มีโอกาสเท่าเทียมกันในการสร้างอัตราการแปลงระหว่าง 0 ถึง 100% ดังนั้นจึงมีความเท่าเทียมกันของปุ่มตั้งแต่เริ่มต้น — ทั้งคู่มีโอกาส 50% ที่จะเป็นนักแสดงชั้นนำ
จากนั้นการทดสอบจะเริ่มขึ้นและรวบรวมข้อมูล จากการสังเกตข้อมูลใหม่ ผู้ทดสอบ A/B ของ Bayesian จะอัปเดตความรู้ของตน ดังนั้น ถ้า B แสดงสัญญา พวกเขาสามารถเข้าถึงความเชื่อภายหลังตามข้อสังเกตนั้นว่า "B มีโอกาส 61% ที่จะชนะ A"
มีความแตกต่างหลักระหว่างสองวิธี
นั่นเป็นเหตุผลสำคัญที่เราต้องรักษาแนวทางที่เป็นกลางในการทดสอบ A/B แบบเบย์
เครื่องมือทดสอบ A/B ของ Bayesian ส่วนใหญ่ - อาจเป็นเพื่อวัตถุประสงค์ทางการตลาด - ใช้จุดยืนต่อต้านความถี่ที่ร้ายแรงและผลักดันข้อโต้แย้งว่า Bayesian ดีกว่าที่จะบอกคุณว่าตัวแปรใด "ทำกำไรได้" มากกว่า
แต่วิธีการทางสถิติเดียวในการทดสอบ A/B นั้นมีสิทธิ์เฉพาะตัวในข้อมูลเชิงลึกหรือไม่
หากมีการผลักดันข้อโต้แย้งแบบเบย์มากขึ้น พวกเขาอาจต้องเผชิญกับการศึกษาที่ผู้ตอบแบบสอบถามกล่าวว่าพวกเขาต้องการทราบว่าแนวทางปฏิบัติที่ดีที่สุดคืออะไร หรือพวกเขาต้องการเพิ่มผลกำไรสูงสุดหรือสิ่งที่คล้ายกัน สิ่งนี้ทำให้คำถามอยู่ในขอบเขตทฤษฎีการตัดสินใจอย่างแน่นหนา - สิ่งที่ทั้งการอนุมานแบบเบย์และการอนุมานแบบใช้บ่อยไม่สามารถพูดได้โดยตรง
Georgi Georgiev ผู้สร้าง Analytics-toolkit.com และผู้เขียน “Statistical Methods in Online A/B Testing”
เราจะเจาะลึกรายละเอียดเหล่านี้โดยย่อในหัวข้อถัดไป ในตอนนี้ เรามาทำให้ไพรเมอร์ที่เหลือนี้ง่ายต่อการเข้าใจกันก่อน
อภิธานศัพท์สั้นๆ ของคำศัพท์ Bayesian ที่มีความสำคัญต่อผู้ทดสอบ A/B
การอนุมานแบบเบย์
การอนุมานแบบเบย์กำลังอัปเดตความน่าจะเป็นสำหรับสมมติฐานด้วยข้อมูลใหม่ มันสร้างขึ้นจากความเชื่อและความน่าจะเป็น
การอนุมานแบบเบย์ใช้ประโยชน์จากความน่าจะเป็นแบบมีเงื่อนไขเพื่อช่วยให้เราเข้าใจว่าข้อมูลส่งผลต่อความเชื่อของเราอย่างไร สมมติว่าเราเริ่มด้วยความเชื่อก่อนว่าท้องฟ้าเป็นสีแดง หลังจากดูข้อมูลบางอย่างแล้ว ในไม่ช้าเราจะรู้ว่าความเชื่อก่อนหน้านี้นี้ผิด ดังนั้นเราจึงดำเนินการอัปเดตแบบเบย์เซียนเพื่อปรับปรุงแบบจำลองที่ไม่ถูกต้องเกี่ยวกับสีของท้องฟ้า และจบลงด้วยความเชื่อทางด้านหลังที่แม่นยำยิ่งขึ้น
Michael Berk ใน Towards Data Science
ความน่าจะเป็นแบบมีเงื่อนไข
ความน่าจะเป็นแบบมีเงื่อนไขคือความน่าจะเป็นของเหตุการณ์หนึ่งที่มีเหตุการณ์อื่นเกิดขึ้น นั่นคือ ความน่าจะเป็นของ A ภายใต้เงื่อนไข B
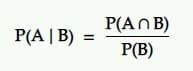
การ แปล: ความน่าจะเป็นของเหตุการณ์ A ที่เกิดขึ้นจากเหตุการณ์อื่น B เท่ากับความน่าจะเป็นของ B และ A ที่เกิดขึ้นร่วมกันหารด้วยความน่าจะเป็นของเหตุการณ์ B
การกระจายความน่าจะเป็น/การกระจายความน่าจะเป็น
การแจกแจงความน่าจะเป็นคือการแจกแจงที่แสดงว่าข้อมูลของคุณจะถือว่าค่าเฉพาะนั้นเป็นไปได้มากน้อยเพียงใด
ในกรณีที่ข้อมูลของคุณสามารถสมมติค่าได้หลายค่า เช่น หมวดหมู่ เช่น สี ซึ่งอาจเป็นสีเทา สีแดง สีส้ม สีฟ้า ฯลฯ การกระจายของคุณเป็นแบบพหุนาม สำหรับชุดตัวเลข การแจกแจงอาจเป็นปกติ และสำหรับค่าข้อมูลที่อาจเป็นใช่/ไม่ใช่ หรือ จริง/เท็จ จะเป็นแบบทวินาม
การกระจายความเชื่อก่อนหน้า
หรือการแจกแจงความน่าจะเป็นก่อนหน้า เรียกง่ายๆ ว่าก่อน เป็นการแสดงออกถึงความเชื่อของคุณก่อนที่คุณจะได้รับหลักฐานของข้อมูลใหม่ ดังนั้นจึงเป็นการแสดงออกถึงความเชื่อเริ่มต้นของคุณซึ่งคุณจะอัปเดตหลังจากพิจารณาหลักฐานบางอย่างโดยใช้การวิเคราะห์แบบเบย์ (หรือการอนุมาน)
คอนจูกาซี
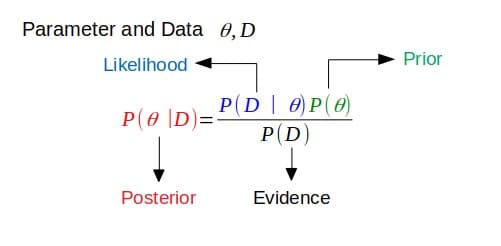
ประการแรก คอนจูเกตหมายถึงการรวมเข้าด้วยกัน มักจะเป็นคู่ ในทฤษฎีความน่าจะเป็นแบบเบย์ คอนจูกาซีจะถือว่าก่อนหน้านั้นคอนจูเกตกับความน่าจะเป็น
ถ้าส่วนหลังมีรูปแบบการทำงานเหมือนกับก่อนหน้า ดังนั้นค่าก่อนหน้าจะผสานกับฟังก์ชันความน่าจะเป็น นี่แสดงให้เห็นว่าฟังก์ชันความน่าจะเป็นจะอัปเดตการแจกแจงก่อนหน้าอย่างไร
Conjugate Priors
สิ่งนี้เชื่อมโยงกับคำจำกัดความข้างต้น ถ้าหลังอยู่ในกลุ่มการกระจายความน่าจะเป็นเดียวกัน (หรือมีรูปแบบการทำงานเหมือนกัน) กับการแจกแจงความน่าจะเป็นก่อนหน้า การแจกแจงก่อนหน้าและหลังจะเป็นการแจกแจงแบบคอนจูเกต ในกรณีนี้ ค่าก่อนหน้านี้เรียกว่าคอนจูเกตก่อนสำหรับฟังก์ชันความน่าจะเป็น
พวกเขาอาจเป็นอัตนัย (ตามความรู้ของผู้ทดลอง) วัตถุประสงค์และข้อมูล (ตามข้อมูลทางประวัติศาสตร์) หรือไม่ใช่ข้อมูล
ฟังก์ชั่นการสูญเสีย
ฟังก์ชันการสูญเสียเป็นวิธีการหาปริมาณการสูญเสียโดยการวัดว่าค่าประมาณปัจจุบันของเราแย่แค่ไหน ช่วยให้เราลดการสูญเสียสำหรับการทดสอบสมมติฐาน โดยเฉพาะอย่างยิ่งเมื่อแสดงการอนุมานซึ่งอยู่ในช่วงของค่าที่น่าจะเป็นไปได้ และสนับสนุนการตัดสินใจด้วยผลการทดสอบของเรา
หมดหนทางแล้ว เราไปต่อได้
หากคุณเคยอยู่แถวนี้มาระยะหนึ่งแล้ว คุณอาจเจอมส์สถิติ Frequentist vs Bayesian มากกว่าสองสามแบบ

ทั้งสองฝ่ายดูเหมือนจะค้นหาคำตอบจากทิศทางตรงกันข้าม แต่เป็นเช่นนั้นจริงหรือ? เพื่อให้เข้าใจดีขึ้น (ในขณะที่ยังคงเป็นกลาง) ให้ไปที่ค่าย Frequentists
สถิติความถี่คืออะไร?
นี่เป็นเทคนิคอนุมานแรกที่คนส่วนใหญ่เรียนรู้ในสถิติ สถิติที่ใช้บ่อยคำนวณความน่าจะเป็นที่เหตุการณ์ (สมมติฐาน) เกิดขึ้นบ่อยครั้งภายใต้เงื่อนไขเดียวกัน
การทดสอบสมมติฐาน A/B โดยใช้วิธีการที่ใช้บ่อยมีขั้นตอนดังนี้:
- ประกาศสมมติฐานบางอย่าง โดยทั่วไป สมมติฐานว่างคือตัวแปรใหม่ “B” ไม่ได้ดีไปกว่า “A” ดั้งเดิมในขณะที่สมมติฐานทางเลือกประกาศตรงกันข้าม
- กำหนดขนาดตัวอย่างล่วงหน้าโดยใช้การคำนวณกำลังทางสถิติ เว้นแต่คุณจะใช้วิธีการทดสอบตามลำดับ ใช้เครื่องคำนวณขนาดตัวอย่างซึ่งพิจารณากำลังทางสถิติ อัตราการแปลงปัจจุบัน และผลที่ตรวจพบขั้นต่ำ
- เรียกใช้การทดสอบ และรอให้แต่ละรูปแบบได้สัมผัสกับขนาดตัวอย่างที่กำหนดไว้ล่วงหน้า
- คำนวณความน่าจะเป็นของการสังเกตผลลัพธ์อย่างน้อยที่สุดเท่ากับข้อมูลภายใต้สมมติฐานว่าง (p-value) ปฏิเสธสมมติฐานว่างและปรับใช้ตัวแปรใหม่กับการใช้งานจริงหากค่า p < 5%
สิ่งนี้เปรียบเทียบกับ Bayesian ได้อย่างไร มาดูกัน…
การทดสอบ A/B แบบ Bayesian กับ Frequentist
นี่เป็นการอภิปรายที่มีชื่อเสียงในทุกที่ที่มีการอนุมานทางสถิติ และบอกตรงๆ ว่าไร้สาระ ทั้งสองมีข้อดีและกรณีที่เป็นวิธีที่ดีที่สุดในการใช้
ตรงกันข้ามกับสิ่งที่คุณคิดในโปรโมเตอร์ส่วนใหญ่ในทั้งสองค่าย พวกเขามีความคล้ายคลึงกันในหลาย ๆ ด้านและไม่ได้ใกล้ชิดกับความจริงมากไปกว่าที่อื่น ๆ แม้ว่าแนวทางของพวกเขาจะแตกต่างกัน
ตัวอย่างเช่น เมื่อนำไปใช้กับการทดสอบ A/B ไม่มีวิธีใดที่เจาะจงที่จะให้การคาดการณ์ที่แม่นยำและแม่นยำในแง่ของการดำเนินการที่จะทำให้ธุรกิจเติบโต การทดสอบ A/B ช่วยให้คุณขจัดความเสี่ยงออกจากการตัดสินใจได้
ไม่ว่าคุณจะวิเคราะห์ข้อมูลด้วยวิธีใด โดยใช้วิธีการแบบ Bayesian หรือ Frequentist คุณสามารถดำเนินการได้ด้วยความมั่นใจว่าคุณพูดถูกในระดับหนึ่ง
และด้วยเหตุนั้น แบบจำลองทางสถิติทั้งสองแบบจึงถูกต้อง Bayesian อาจมีข้อได้เปรียบด้านความเร็ว แต่มีความต้องการด้านการคำนวณมากกว่า Frequentist
ตรวจสอบความแตกต่างอื่น ๆ ...
กรอบงานบ่อย
พวกเราส่วนใหญ่คุ้นเคยกับแนวทางที่ใช้บ่อยจากหลักสูตรสถิติเบื้องต้น เราได้กำหนดวิธีการข้างต้น — ตั้งแต่การประกาศสมมติฐานว่าง การกำหนดขนาดตัวอย่าง การรวบรวมข้อมูลผ่านการทดลองแบบสุ่ม และในที่สุดก็สังเกตผลลัพธ์ที่มีนัยสำคัญทางสถิติ
ใน Frequentism เรามองว่าความน่าจะเป็นนั้นสัมพันธ์กับความถี่ของเหตุการณ์ที่เกิดซ้ำ ดังนั้น ในการโยนเหรียญที่ยุติธรรม นักเล่นประจำเชื่อว่าหากพวกเขาเดาบ่อยพอ พวกเขาจะได้หัวที่ถูกต้อง 50% ของเวลา และเช่นเดียวกันสำหรับก้อย
Frequentist mindset: “ถ้าฉันทำการทดลองซ้ำในเงื่อนไขเดิมซ้ำแล้วซ้ำเล่า วิธีของฉันจะได้คำตอบที่ถูกต้องมีมากแค่ไหน”
กรอบการทำงานแบบเบย์
ในขณะที่แนวทางที่ใช้บ่อยถือว่าพารามิเตอร์ประชากรสำหรับตัวแปรแต่ละตัวเป็นค่าคงที่ (ไม่ทราบ) วิธีแบบเบย์จะจำลองค่าพารามิเตอร์แต่ละค่าเป็นตัวแปรสุ่มพร้อมการแจกแจงความน่าจะเป็นบางส่วน
ที่นี่ คุณคำนวณการแจกแจงความน่าจะเป็น (และค่าที่คาดไว้) สำหรับพารามิเตอร์ที่สนใจโดยตรง
และเพื่อจำลองการกระจายความน่าจะเป็นสำหรับตัวแปรแต่ละตัว เราอาศัยกฎของเบย์เพื่อรวมผลการทดสอบกับความรู้ก่อนหน้าใดๆ ที่เรามีเกี่ยวกับเมตริกที่น่าสนใจ เราสามารถลดความซับซ้อนของการคำนวณโดยใช้คอนจูเกตก่อน
Alex Birkett สรุปอัลกอริทึมแบบเบย์ดังนี้:
- กำหนดการกระจายก่อนหน้าที่รวมเอาความเชื่อส่วนตัวของคุณเกี่ยวกับพารามิเตอร์ ก่อนหน้านี้อาจไม่มีข้อมูลหรือให้ข้อมูล
- รวบรวมข้อมูล
- อัปเดตการแจกแจงก่อนหน้าของคุณด้วยข้อมูลโดยใช้ทฤษฎีบทของเบย์ (แม้ว่าคุณจะมีวิธีแบบเบย์โดยไม่ต้องใช้กฎของเบย์อย่างชัดแจ้ง—ดูแบบไม่มีพารามิเตอร์แบบอิงพารามิเตอร์) เพื่อรับการแจกแจงหลัง การแจกแจงหลังเป็นการแจกแจงความน่าจะเป็นที่แสดงถึงความเชื่อที่อัปเดตของคุณเกี่ยวกับพารามิเตอร์หลังจากดูข้อมูลแล้ว
- วิเคราะห์การแจกแจงหลังและสรุป (mean, median, sd, quantiles…)
กล่าวโดยสรุป ผู้ทดลองแบบเบย์มุ่งเน้นไปที่มุมมองของตนเองและความน่าจะเป็นที่มีความหมายต่อพวกเขา ความคิดเห็นของพวกเขาวิวัฒนาการด้วยข้อมูลที่สังเกตได้ ในทางกลับกันผู้ที่มาบ่อยเชื่อว่าคำตอบที่ถูกต้องอยู่ที่ไหนสักแห่ง

เข้าใจว่าการโต้วาทีบ่อยครั้งและแบบเบส์ไม่ส่งผลกระทบต่อการวิเคราะห์หลังการทดสอบ A/B มากขนาดนั้น ความแตกต่างที่สำคัญระหว่างทั้งสองค่ายนั้นสัมพันธ์กับสิ่งที่สามารถทดสอบได้มากกว่า
โดยทั่วไปแล้วสถิติความน่าจะเป็นจะไม่ถูกนำมาใช้ในการวิเคราะห์ในภายหลัง อาร์กิวเมนต์ Bayesian-Frequentist ใช้ได้กับการเลือกตัวแปรที่จะทดสอบในกระบวนทัศน์ A/B มากกว่า แต่ถึงแม้จะมีผู้ทดสอบ A/B ส่วนใหญ่ก็ยังฝ่าฝืนสมมติฐานการวิจัย ความน่าจะเป็น และช่วงความเชื่อมั่น
ดร.ร็อบ บาลอน ถึง CXL
Georgi อธิบายเพิ่มเติมว่า:
มีเครื่องคิดเลข Bayesian ออนไลน์หลายเครื่องและผู้จำหน่ายซอฟต์แวร์ทดสอบ A/B รายใหญ่อย่างน้อยหนึ่งรายที่ใช้เอ็นจิ้นทางสถิติแบบเบย์ซึ่งทั้งหมดใช้สิ่งที่เรียกว่านักบวชที่ไม่ให้ข้อมูล (เรียกชื่อผิดนิดหน่อย แต่อย่าเจาะลึกเรื่องนี้) ในกรณีส่วนใหญ่ ผลลัพธ์จากเครื่องมือเหล่านี้ตรงกับตัวเลขกับผลลัพธ์จากการทดสอบบ่อยครั้งในข้อมูลเดียวกัน สมมติว่าเครื่องมือ Bayesian จะรายงานบางอย่างเช่น 'ความน่าจะเป็น 96% ที่ B ดีกว่า A' ในขณะที่เครื่องมือที่ใช้บ่อยจะสร้างค่า p ที่ 0.04 ซึ่งสอดคล้องกับระดับความเชื่อมั่น 96%
ในสถานการณ์เช่นนี้ ซึ่งพบได้ทั่วไปมากกว่าที่บางคนต้องการยอมรับ ทั้งสองวิธีจะนำไปสู่การอนุมานเดียวกัน และระดับของความไม่แน่นอนจะเท่ากัน แม้ว่าการตีความจะต่างกัน
ชาวเบย์จะพูดอะไรเกี่ยวกับผลลัพธ์นี้ มันเปลี่ยนค่า p เป็นความน่าจะเป็นหลังที่เหมาะสมเมื่อดูสถานการณ์ที่ไม่มีข้อมูลก่อนหน้าหรือไม่? หรือแอปพลิเคชันทั้งหมดของการทดสอบแบบเบย์เหล่านี้เข้าใจผิดสำหรับการใช้แบบไม่มีข้อมูลก่อนหน้าต่อ se?
ไม่จำเป็นต้องเลือกค่ายและหาจุดหลังที่กำบังเพื่อปาก้อนหินที่ค่ายอื่น มีหลักฐานว่าเฟรมเวิร์กทั้งสองให้ผลลัพธ์ที่เหมือนกัน ไม่ว่าจะเลือกทางไหน ปลายทางก็คงจะเหมือนเดิม ขึ้นอยู่กับว่าคุณจะไปที่นั่นด้วย Frequentist vs Bayesian ได้อย่างไร
ตัวอย่างเช่น:
- มีข้อมูลที่แสดงว่าการทดสอบแบบเบย์นั้นเร็วกว่าและเป็นตัวเลือกที่ต้องการสำหรับการทดสอบเชิงโต้ตอบ:
เนื่องจากกระบวนทัศน์แบบเบย์ทำให้ผู้ทดลองสามารถหาปริมาณความเชื่ออย่างเป็นทางการและรวมความรู้เพิ่มเติมเข้าด้วยกัน จึงเร็วกว่าการวิเคราะห์ทางสถิติแบบเดิม
ในการจำลองการทดสอบ A/B แบบเบย์ เมื่อมีการปรับเกณฑ์การตัดสินใจ (เช่น เพิ่มความทนทานต่อข้อผิดพลาด) 75% ของการทดลองสรุปได้ภายใน 22.7% ของการสังเกตที่กำหนดโดยวิธีการแบบเดิม (ที่ระดับนัยสำคัญ 5%) และบันทึกข้อผิดพลาดประเภท II เพียง 10% เท่านั้น - Bayesian ยังถือว่าให้อภัยมากกว่า ในขณะที่ Frequentist ไม่ชอบความเสี่ยง:
แม้ว่าการทดสอบ Frequentist จำนวนมากใช้นัยสำคัญทางสถิติที่ 95% แต่ Bayesian ก็พอใจได้น้อยกว่านั้น หากตัวแปรมีโอกาส 78% ที่จะเอาชนะส่วนควบคุม ขึ้นอยู่กับการสูญเสียที่คาดหวัง อาจเป็นการตัดสินใจที่ดีที่จะ "ปรับใช้ตัวแปรนั้น"
หากคุณผิดและคาดว่าจะขาดทุนน้อยกว่าร้อยละ นั่นเป็นความเสียหายเล็กน้อยสำหรับธุรกิจจำนวนมาก แนวทางที่กระท่อนกระแท่นนี้อาจเหมาะกว่าสำหรับการตัดสินใจอย่างรวดเร็วในสถานการณ์ที่มีความเสี่ยงต่ำมาก - อย่างไรก็ตาม การจำลองและการคำนวณแบบเบย์นั้นใช้การคำนวณอย่างหนัก:
ในทางกลับกัน frequentist นั้นใช้ปากกาและกระดาษ คำเตือน: หากเครื่องมือทดสอบ A/B ของคุณใช้ Bayesian และคุณไม่ทราบว่ามีการเพิ่มสมมติฐานใดในข้อมูลของคุณ คุณจะไม่สามารถพึ่งพา "คำตอบ" ที่ผู้ขายของคุณมอบให้คุณได้ ใช้เกลือเล็กน้อย และดำเนินการวิเคราะห์ของคุณเอง
ไม่ใช่แสงแดดและรุ้งกับเบย์เซียน เช่นเดียวกับ Georgi ชี้ให้เห็นรายการคำถามนี้:
- “คุณต้องการได้ผลลัพธ์ของความน่าจะเป็นก่อนหน้าและฟังก์ชันความน่าจะเป็นหรือไม่”
- “คุณต้องการผสมระหว่างความน่าจะเป็นและข้อมูลก่อนหน้าเป็นผลลัพธ์หรือไม่”
- “คุณต้องการความเชื่อส่วนตัวผสมกับข้อมูลเพื่อสร้างผลลัพธ์หรือไม่” (ถ้าใช้ข้อมูลก่อน)
- “คุณสะดวกไหมที่จะนำเสนอสถิติซึ่งมีข้อมูลก่อนหน้านี้ที่สันนิษฐานว่ามีความแน่นอนสูงผสมกับข้อมูลจริง”
สิ่งเหล่านี้เป็นสถิติแบบเบย์ทั้งหมดในแง่ของฆราวาส
สถิติแบบเบย์บอกอะไรคุณได้บ้างในการทดสอบ A/B?
คุณออกแบบการทดสอบ A/B เพื่อให้ข้อมูลเชิงลึกว่าการเปลี่ยนแปลงส่งผลต่อเมตริกที่คุณสนใจอย่างไร เช่น อัตรา Conversion หรือรายได้ต่อผู้เข้าชม
เมื่อคุณใช้เครื่องมือที่ทำงานร่วมกับสถิติแบบเบย์ สิ่งสำคัญคือต้องเข้าใจว่าผลลัพธ์ของคุณหมายถึงอะไร เพราะ "B คือผู้ชนะ" ไม่ได้หมายความว่าสิ่งที่คนส่วนใหญ่คิดจะทำอย่างแน่นอน
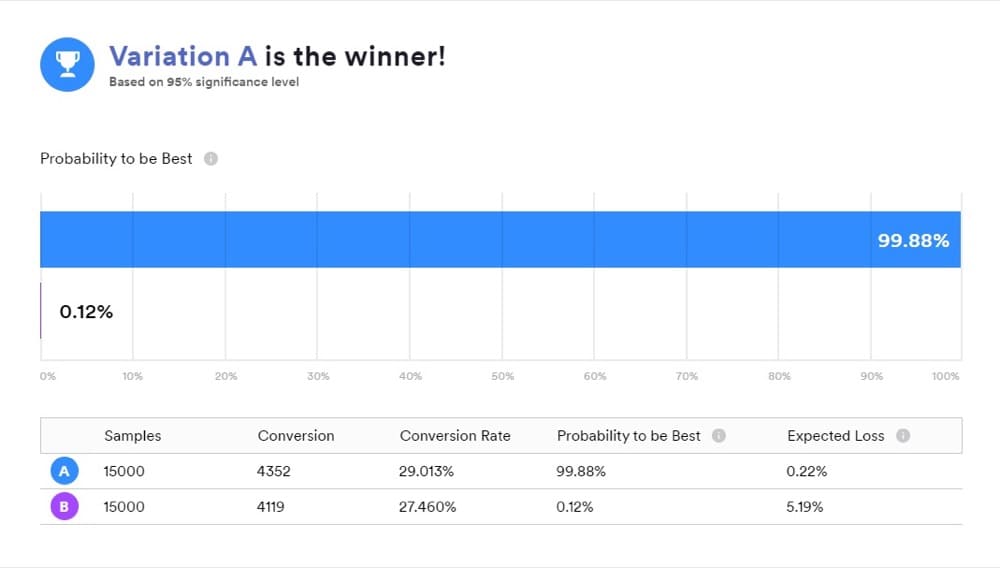
เป็นวิธีที่สะดวกในการนำเสนอผลลัพธ์ แต่นั่นไม่ใช่สิ่งที่การทดสอบของคุณเปิดเผย คำตอบที่คุณต้องการจะอยู่ในการเปรียบเทียบด้านหลังของ "A" และ "B"
เปรียบเทียบได้ 3 วิธีดังนี้
ความน่าจะเป็นที่จะดีที่สุด (P2BB)
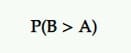
นี่คือความน่าจะเป็นที่จะประกาศผู้ชนะในการทดสอบ A/B แบบเบย์
ตัวแปรที่มีความเป็นไปได้ที่จะดีที่สุดคือตัวแปรที่มีความเป็นไปได้สูงที่สุดที่จะทำผลงานได้ดีกว่าอีกตัวเลือกหนึ่ง
ซึ่งคำนวณจากชุดตัวอย่างหลังของการวัดดอกเบี้ยจากต้นฉบับและผู้ท้าชิง
ดังนั้น หาก B มีความเป็นไปได้สูงที่สุดในการเพิ่มอัตราการแปลงของคุณ ตัวอย่างเช่น B จะถูกประกาศให้เป็นผู้ชนะ
ความคาดหวังที่เพิ่มขึ้น
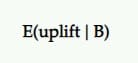
แล้วถ้า B เป็นผู้ชนะ เราควรคาดหวังการยกระดับมากแค่ไหน? มันจะยังคงให้ผลลัพธ์แบบเดียวกับที่เราเห็นในการทดสอบหรือไม่?
นั่นคือข้อมูลเชิงลึกที่คาดว่าจะได้รับการยกระดับขึ้น การเพิ่มขึ้นที่คาดไว้ของการเลือก B ส่วน A โดยให้ชุดตัวอย่างด้านหลัง ถูกกำหนดเป็นช่วงที่น่าเชื่อถือ (หรือค่าเฉลี่ย) ของเปอร์เซ็นต์ที่เพิ่มขึ้น
ในการทดสอบ A/B เรามักจะเปรียบเทียบสิ่งนี้ว่าเป็นผู้ท้าชิงกับกลุ่มควบคุม ดังนั้น หากผู้ท้าชิงแพ้ มันจะแสดงเป็นค่าลบ (เช่น -11.35%) และค่าบวก (เช่น +9.58%) หากชนะ
ขาดทุนที่คาดหวัง
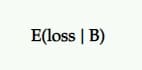
เนื่องจากไม่มีความน่าจะเป็น 100% ที่ B ดีกว่า A จึงมีโอกาสที่จะบันทึกการสูญเสียหากคุณเลือก B ส่วน A ซึ่งแสดงเป็นการสูญเสียที่คาดหวัง และเช่นเดียวกับการเพิ่มขึ้นที่คาดหวัง มันแสดงจาก มุมมองของผู้ท้าชิงกับการควบคุม
มันบอกคุณถึงความเสี่ยงในการเลือกตัวแปร P2BB ของคุณ (เช่น ผู้ชนะที่ประกาศแล้ว)
ก่อนที่เราจะดำดิ่งสู่ตำนาน ขอขอบคุณนักวิเคราะห์ตำนาน Georgi Georgiev การวิเคราะห์เชิงลึกของเขาเกี่ยวกับการอนุมานที่ใช้บ่อยเทียบกับแบบเบย์ และความน่าจะเป็นและสถิติแบบเบย์ในการทดสอบ A/B เป็นแรงบันดาลใจในส่วนถัดไป
ตำนานเกี่ยวกับสถิติแบบเบย์ที่ควรหลีกเลี่ยง
ด้วยการแข่งขันที่เกือบจะเก่าเท่าที่ไม่จำเป็น การดีเบตแบบ Bayesian vs Frequentist ได้รวบรวมข้อมูลจำนวนมาก — และก่อให้เกิดตำนานมากมาย
ตำนานที่ใหญ่ที่สุดเหล่านี้ (ตำนาน #2) ได้รับการส่งเสริมโดยผู้จำหน่ายเครื่องมือทดสอบ A/B เพื่อบอกคุณว่าเหตุใดวิธีการหนึ่งจึงดีกว่าอีกวิธีหนึ่ง
แต่หลังจากอ่านหัวข้อด้านบนแล้ว คุณก็รู้ดีขึ้น
มาเปิดเผยหลุมในตำนานเหล่านี้กัน
ตำนาน # 1: Bayesians ระบุสมมติฐานของพวกเขา Frequentists Don't
นี่แสดงให้เห็นว่าชาวเบย์ตั้งสมมติฐานในรูปแบบของการแจกแจงล่วงหน้าและเปิดให้ประเมินได้ แต่ผู้ที่มักใช้บ่อยมักตั้งสมมติฐานที่ซ่อนอยู่ตรงกลางคณิตศาสตร์
ทำไมมันผิด: Bayesians และ Frequentists สร้างสมมติฐานพื้นฐานที่คล้ายกัน ความแตกต่างเพียงอย่างเดียวคือ Bayesians สร้างสมมติฐานเพิ่มเติม — ด้านบนของคณิตศาสตร์
แบบจำลองที่ใช้บ่อยใช้สมมติฐานในการคำนวณ เช่น รูปร่างของการกระจาย ความเหมือนกันหรือความแตกต่างของผลกระทบจากการสังเกต และความเป็นอิสระของการสังเกต และพวกเขาไม่ได้ซ่อนเร้น อันที่จริง มีการพูดคุยกันอย่างกว้างขวางในชุมชนทางสถิติและระบุไว้สำหรับการทดสอบทางสถิติที่ใช้บ่อยทุกครั้ง
ความจริง: ผู้ที่ใช้บ่อยระบุสมมติฐานของตนอย่างชัดเจนและดำเนินการอีกขั้นเพื่อทดสอบสมมติฐาน: การทดสอบความปกติ การทดสอบความพอดี (ซึ่งเรามีการทดสอบอัตราส่วนตัวอย่างที่ไม่ตรงกัน) และอื่นๆ
ตำนาน # 2 วิธีการแบบเบย์ให้คำตอบที่คุณต้องการจริงๆ
ความเข้าใจผิดที่นี่คือ p-values และช่วงความเชื่อมั่นไม่ได้บอกผู้ทดสอบถึงสิ่งที่พวกเขาต้องการทราบ ในขณะที่ความน่าจะเป็นหลังและช่วงที่น่าเชื่อถือทำ คนอยากรู้เรื่องเช่น
- ความน่าจะเป็นที่ B ทำได้ดีกว่า A และ
- โอกาสที่ผลลัพธ์จะไม่ใช่เรื่องบังเอิญ
การทดสอบค่า P และสมมติฐาน (การอนุมานตรง) ไม่ได้ให้ข้อมูลนั้น แต่การอนุมานแบบผกผันให้
ทำไมมันผิด: นี่เป็นคำถามเกี่ยวกับภาษาศาสตร์ โดยทั่วไป เมื่อผู้ที่ไม่ใช่นักสถิติใช้คำต่างๆ เช่น "ความน่าจะเป็น" "โอกาส" และ "ความน่าจะเป็น" พวกเขาไม่ได้ใช้คำเหล่านี้โดยคำนึงถึงความหมายทางเทคนิคในใจ สำรวจให้ลึกขึ้นและคุณจะพบว่าพวกเขาสับสนเกี่ยวกับการอนุมานแบบผกผันพอ ๆ กับการอนุมานแบบตรง
ตามที่ Georgi Georgiev คำถามเหล่านี้เริ่มปรากฏขึ้น:
- “ ความ น่าจะเป็นก่อนหน้าคืออะไร? มันนำมาซึ่งคุณค่าอะไร?”
- “ฟังก์ชันความน่าจะเป็นคืออะไร”
- “ความน่าจะเป็น 'ก่อนหน้า' คืออะไร ฉันไม่มีข้อมูลก่อนหน้านี้”
- “ฉันจะปกป้องทางเลือกของความน่าจะเป็นก่อนหน้าได้อย่างไร”
- “มีวิธีสื่อสารตามที่ข้อมูลพูดโดยไม่มีส่วนผสมเหล่านี้หรือไม่”
ความจริง: ควรมีข้อมูลเชิงลึกที่ดีกว่าในสิ่งที่ผู้ทดสอบต้องการทราบ ไม่ใช่การตีความข้อกำหนดทางเทคนิคที่ผิด ค่า P ช่วงความเชื่อมั่น และอื่นๆ จะบอกคุณว่าผลลัพธ์ที่ได้นั้นผ่านการสอบสวนมาอย่างดีเพียงใดจากข้อมูลที่รวบรวมมา พวกเขาให้การวัดความแน่นอนโดยไม่มีอิทธิพลของสมมติฐานส่วนตัวที่ไม่ได้ทดสอบก่อน
ตำนาน #3: การอนุมานแบบเบย์ช่วยให้คุณสื่อสารความไม่แน่นอนได้ดีกว่าการอนุมานบ่อยๆ
เนื่องจากผลการทดสอบทำให้เกิดความเข้าใจที่ "มีความหมาย" มากขึ้น
ทำไมจึงผิด: ทั้ง Frequentist และ Bayesian มีเครื่องมือที่คล้ายคลึงกันเพื่อช่วยให้คุณสื่อสารความแน่นอนและผลการทดสอบ A/B ของคุณ
| frequentist | เบย์เซียน | ||||||||||
| ● ประมาณการคะแนน | ● ประมาณการคะแนน | ||||||||||
| ● ค่า P | ● ช่วงเวลาที่น่าเชื่อถือ | ||||||||||
| ● ช่วงความเชื่อมั่น | ● ปัจจัยเบส์ | ||||||||||
| ● เส้นโค้งค่า P | ● การแจกแจงหลัง (ทำภารกิจเดียวกันให้สำเร็จ เป็นเส้นโค้งความถี่) | ||||||||||
| ● เส้นความมั่นใจ | |||||||||||
| ● เส้นโค้งความรุนแรง ฯลฯ |
ความจริง: ทุกอย่างขึ้นอยู่กับว่าคุณใช้มันอย่างไร ทั้งสองวิธีมีประสิทธิภาพเท่าเทียมกันในการสื่อสารความไม่แน่นอน อย่างไรก็ตาม มีความแตกต่างในวิธีการนำเสนอการวัดความไม่แน่นอน
ตำนาน #4. ผลการทดสอบ A/B ของ Bayesian มีภูมิคุ้มกันต่อการแอบมอง
นักสถิติแบบเบย์บางคนโต้แย้งว่า "คุณสามารถหยุดการทดสอบแบบเบย์ได้เมื่อคุณเห็น "ผู้ชนะที่ชัดเจน" และทำให้ผลลัพธ์สุดท้ายแตกต่างกันเล็กน้อย
คุณอาจรู้ว่าสิ่งนี้ไม่เป็นที่ยอมรับในการทดสอบบ่อยครั้ง ดังนั้นจึงถือว่าเสียเปรียบเมื่อเทียบกับแบบเบย์เซียน แต่มันจริงเหรอ?
เหตุใดจึงผิด: ในการศึกษาปี 1969 ในวารสาร Royal Statistical Society เรื่อง “การทดสอบความสำคัญซ้ำซ้อนเกี่ยวกับข้อมูลสะสม”, Armitage et al. แสดงให้เห็นว่าการหยุดทางเลือกตามผลลัพธ์เพิ่มความน่าจะเป็นของข้อผิดพลาดได้อย่างไร
คุณไม่สามารถหยุดแค่เมื่อสังเกตเห็นผู้ชนะ อัปเดตส่วนหลังของคุณ และใช้เป็นลำดับถัดไปโดยไม่ต้องปรับวิธีการทำงานของการวิเคราะห์แบบเบย์
ความจริง: Peeking ส่งผลต่อการอนุมานแบบเบย์มากเท่ากับ Frequentist (ถ้าคุณต้องการทำให้ถูกต้อง)
ตำนาน #5. สถิติที่ใช้บ่อยนั้นไม่มีประสิทธิภาพเนื่องจากคุณต้องรอขนาดตัวอย่างคงที่
สมาชิกบางคนของชุมชน CRO เชื่อว่าการทดสอบทางสถิติที่ใช้บ่อยต้องรันด้วยขนาดตัวอย่างที่ตายตัวและถูกกำหนดไว้ล่วงหน้า มิฉะนั้น ผลลัพธ์จะไม่ถูกต้อง
เป็นผลให้คุณรอนานเกินความจำเป็นเพื่อให้ได้ผลลัพธ์ที่คุณต้องการ
ทำไมมันถึงผิด: สถิติที่ใช้บ่อยไม่ได้ถูกใช้แบบนั้นมาเป็นเวลาประมาณเจ็ดทศวรรษแล้ว ด้วยการทดสอบตามลำดับความถี่ คุณไม่จำเป็นต้องกำหนดระยะเวลาที่กำหนดไว้ล่วงหน้าแบบตายตัว
ความจริง: การทดสอบตามลำดับซึ่งเป็นที่นิยมมากขึ้นในปัจจุบัน ต้องใช้ขนาดตัวอย่าง สูงสุด เพื่อสร้างสมดุลระหว่างข้อผิดพลาดประเภท I และประเภท II แต่ขนาดตัวอย่างจริงที่ใช้จะแตกต่างกันไปในแต่ละกรณี ขึ้นอยู่กับผลลัพธ์ที่สังเกตได้
ดังนั้นคุณควรเลือก Bayesian หรือ Frequentist หรือไม่? มีที่สำหรับทั้งคู่
ไม่จำเป็นต้องเลือกข้าง ทั้งสองวิธีมีสถานที่ของพวกเขา ตัวอย่างเช่น โครงการระยะยาวที่ใช้ตัวก่อนหน้าที่อัปเดตและต้องการผลลัพธ์ที่รวดเร็วจะได้ผลดีกว่าด้วยแนวทางแบบเบย์
ในทางกลับกัน วิธี Frequentist เหมาะที่สุดสำหรับโครงการที่ต้องการความสามารถในการทำซ้ำจำนวนมากในผลลัพธ์ เช่นในการเขียนซอฟต์แวร์ที่หลายคนที่มีชุดข้อมูลจำนวนมากจะใช้
Cassie Kozyrkov หัวหน้าหน่วยข่าวกรองการตัดสินใจของ Google กล่าวว่า "สถิติคือศาสตร์แห่งการเปลี่ยนความคิดของคุณภายใต้ความไม่แน่นอน"
ในวิดีโอสรุปสถิติ Bayesian vs Frequentist ของเธอ เธอกล่าวว่า:
“คุณสามารถใช้การอภิปรายของ Frequentist และ Bayesian แล้วยุบลงไปที่สิ่งที่คุณกำลังเปลี่ยนใจ ผู้ที่มาบ่อยเปลี่ยนใจเกี่ยวกับการกระทำ พวกเขามีการกระทำผิดนัดมากกว่า — บางทีพวกเขาอาจไม่มีความเชื่อ — แต่พวกเขามีการกระทำที่พวกเขาชอบภายใต้ความเขลา แล้วพวกเขาก็ถามว่า “หลักฐานของฉัน [หรือข้อมูล] ทำให้ฉันเปลี่ยนใจหรือไม่ การกระทำนั้น?” “ฉันรู้สึกไร้สาระที่ทำมันโดยอาศัยหลักฐานของฉันหรือเปล่า”
ในทางกลับกัน ชาวเบย์เปลี่ยนใจไปในทางที่ต่างออกไป พวกเขาเริ่มต้นด้วยความคิดเห็น ความคิดเห็นส่วนตัวที่แสดงออกทางคณิตศาสตร์ เรียกว่า ก่อน แล้วจึงถามว่า "ความคิดเห็นที่สมเหตุสมผลที่ฉันควรมีหลังจากรวมหลักฐานแล้วคืออะไร" ดังนั้นผู้ที่ใช้บ่อยจึงเปลี่ยนใจเกี่ยวกับการกระทำ ชาวเบย์จึงเปลี่ยนความคิดเกี่ยวกับความเชื่อ
และขึ้นอยู่กับว่าคุณต้องการวางกรอบการตัดสินใจอย่างไร คุณอาจจะชอบไปกับค่ายหนึ่งมากกว่าที่อื่น”
ในท้ายที่สุด เราทุกคนต่างมุ่งไปสู่ข้อสรุปที่คล้ายคลึงกัน — ความแตกต่างอยู่ที่วิธีการนำเสนอข้อสรุปเหล่านั้นแก่คุณ
หากการอนุมานความถี่สูงและแบบเบย์เป็นฟังก์ชันการเขียนโปรแกรม โดยที่อินพุตเป็นปัญหาทางสถิติ ทั้งสองจะมีความแตกต่างกันในสิ่งที่พวกเขาส่งคืนให้กับผู้ใช้ ฟังก์ชันอนุมานที่ใช้บ่อยจะส่งกลับตัวเลข แทนค่าประมาณ (โดยทั่วไปจะเป็นสถิติสรุป เช่น ค่าเฉลี่ยตัวอย่าง เป็นต้น) ในขณะที่ฟังก์ชันเบย์เซียนจะส่งกลับค่าความน่าจะเป็น
ตัดตอนมาจากหนังสือ “Probabilistic Programming & Bayesian Methods for Hackers
สิ่งที่ไม่ถูกต้องนักคือการอ้างว่าฝ่ายหนึ่งให้ผลลัพธ์เชิงปฏิบัติมากกว่าอีกฝ่ายหนึ่ง
ที่สำคัญ Takeaway
สถิติแบบเบย์ในการทดสอบ A/B ประกอบด้วย 4 ขั้นตอนที่แตกต่างกัน:
- ระบุการแจกจ่ายก่อนหน้าของคุณ
- เลือกแบบจำลองทางสถิติที่สะท้อนความเชื่อของคุณ
- ทำการทดลอง
- ใช้ผลลัพธ์เพื่ออัปเดตความเชื่อของคุณและคำนวณการแจกแจงหลัง
ผลลัพธ์ของคุณจะนำคุณไปสู่ความน่าจะเป็นเชิงลึก ดังนั้นคุณจะรู้ว่าตัวแปรใดมีความเป็นไปได้สูงที่สุดที่จะดีที่สุด การสูญเสียที่คาดหวัง และการเพิ่มขึ้นที่คาดหวังของคุณ
เครื่องมือทดสอบ A/B ส่วนใหญ่จะตีความข้อมูลเหล่านี้ให้คุณโดยใช้สถิติแบบเบย์ แต่ผู้ทดลองอย่างละเอียดจะทำการวิเคราะห์หลังการทดสอบเพื่อทำความเข้าใจผลลัพธ์เหล่านั้นให้ดีขึ้น
เนื่องจากคุณมาไกลถึงขนาดนี้ จึงมีข้อเท็จจริงสนุกๆ สำหรับคุณ: คุณรู้จักภาพเหมือนของ Thomas Bayes ที่ทุกคนคุ้นเคยไหม อันนี้:

ไม่มีใครแน่ใจ 100% ว่าเป็นเขา