Ошибки типа I и типа II: неизбежные ошибки в оптимизации

Ошибки типа I и типа II случаются, когда вы ошибочно определяете победителей в своих экспериментах или не можете их обнаружить. С обеими ошибками вы в конечном итоге выбираете то, что работает или нет. И не с реальными результатами.

Неверная интерпретация результатов тестирования не только приводит к ошибочным усилиям по оптимизации, но и может сорвать вашу программу оптимизации в долгосрочной перспективе.

Лучшее время, чтобы поймать эти ошибки, еще до того, как вы их сделаете! Итак, давайте посмотрим, как вы можете избежать ошибок типа I и типа II в своих экспериментах по оптимизации.

Но перед этим давайте посмотрим на нулевую гипотезу… потому что именно ошибочное отклонение или непринятие нулевой гипотезы вызывает ошибки первого и второго рода .

Нулевая гипотеза: ​H0

Когда вы выдвигаете гипотезу об эксперименте, вы не сразу предполагаете, что предлагаемое изменение сдвинет определенный показатель.

Вы начинаете с того, что говорите, что предлагаемое изменение вообще не повлияет на соответствующую метрику — что они не связаны между собой.

Это ваша нулевая гипотеза (H0). H0 всегда означает, что изменений нет. Это то, во что вы верите по умолчанию… пока (и если) ваш эксперимент не опровергнет это.

И ваша альтернативная гипотеза (Ha или H1) состоит в том, что есть положительное изменение. H0 и Ha всегда являются математическими противоположностями. Ха — это та, в которой вы ожидаете, что предлагаемое изменение будет иметь значение, это ваша альтернативная гипотеза — и это то, что вы проверяете в своем эксперименте.

Так, например, если вы хотите провести эксперимент на своей странице с ценами и добавить на нее еще один способ оплаты, вы должны сначала сформулировать нулевую гипотезу, утверждающую: дополнительный способ оплаты не повлияет на продажи. Ваша альтернативная гипотеза будет звучать так: дополнительный способ оплаты увеличит продажи.

Проведение эксперимента, по сути, ставит под сомнение нулевую гипотезу или статус-кво.

Ошибки типа I и типа II происходят, когда вы ошибочно отвергаете или не можете отвергнуть нулевую гипотезу.

Понимание ошибок типа I

Ошибки типа I известны как ложные срабатывания или альфа-ошибки.

В случае ошибки типа I при проверке гипотезы ваш оптимизационный тест или эксперимент * КАЖЕТСЯ УСПЕШНЫМ* , и вы (ошибочно) заключаете, что тестируемый вами вариант работает иначе (лучше или хуже), чем оригинал.

При ошибках типа I вы видите подъемы или спады — которые носят временный характер и вряд ли сохранятся в долгосрочной перспективе — и в конечном итоге отвергаете свою нулевую гипотезу (и принимаете альтернативную гипотезу).

Ошибочное отклонение нулевой гипотезы может произойти по разным причинам, но ведущей из них является практика подглядывания (т. е. просмотр ваших результатов в промежуточный период или во время проведения эксперимента). И вызов тестов раньше, чем будут достигнуты установленные критерии остановки.

Многие методологии тестирования не одобряют практику подглядывания, поскольку просмотр промежуточных результатов может привести к неправильным выводам, что приведет к ошибкам первого рода.

Вот как можно совершить ошибку первого рода:

Предположим, вы оптимизируете целевую страницу своего веб-сайта B2B и предполагаете, что добавление на нее значков или наград уменьшит беспокойство ваших потенциальных клиентов, тем самым увеличив скорость заполнения форм (что приведет к увеличению числа лидов).

Таким образом, ваша нулевая гипотеза для этого эксперимента звучит так: добавление значков не влияет на заполнение форм.

Критерием прекращения такого эксперимента обычно является определенный период и/или после того, как X конверсий произойдет на заданном уровне статистической значимости. Традиционно оптимизаторы стараются достичь отметки статистической достоверности 95%, потому что это оставляет вам 5%-й шанс совершить ошибку первого рода, которая считается достаточно низкой для большинства экспериментов по оптимизации. В целом, чем выше этот показатель, тем ниже вероятность совершения ошибок первого рода.

Уровень достоверности, к которому вы стремитесь, определяет, какова будет вероятность совершения ошибки I рода (α).

Таким образом, если вы стремитесь к доверительному уровню 95%, ваше значение для α становится равным 5%. Здесь вы соглашаетесь с тем, что вероятность того, что ваш вывод может быть неправильным, составляет 5%.

Напротив, если вы используете уровень достоверности 99% в своем эксперименте, ваша вероятность получить ошибку первого рода падает до 1%.

Скажем, для этого эксперимента вы слишком нетерпеливы и вместо того, чтобы ждать окончания эксперимента, вы смотрите на панель инструментов вашего инструмента тестирования (загляните!) всего за день до его начала. И вы замечаете «очевидный» рост — скорость заполнения вашей формы выросла на колоссальные 29,2% с уровнем достоверности 95%.

А БАМ…

… вы прекращаете свой эксперимент.

… отвергнуть нулевую гипотезу (о том, что значки не повлияли на продажи).

… принять альтернативную гипотезу (о том, что значки повышают продажи).

… и запускайте версию со значками наград.

Но когда вы измеряете количество потенциальных клиентов в течение месяца, вы обнаружите, что число почти сопоставимо с тем, что вы указали в исходной версии. В конце концов, значки не имели большого значения. И что нулевая гипотеза, вероятно, была отвергнута напрасно.

Здесь произошло то, что вы закончили свой эксперимент слишком рано, отвергли нулевую гипотезу и в итоге получили ложного победителя — совершив ошибку первого рода.

Как избежать ошибок типа I в ваших экспериментах

Один из верных способов снизить ваши шансы на совершение ошибки первого рода — использовать более высокий уровень достоверности. Приемлем уровень статистической значимости 5% (что соответствует уровню статистической достоверности 95%). Это ставка, которую сделали бы большинство оптимизаторов, потому что здесь вы потерпите неудачу в маловероятном диапазоне 5%.

Помимо установки высокого уровня достоверности, важно проводить тесты достаточно долго. Калькуляторы продолжительности теста могут подсказать вам, как долго вы должны проводить тест (после учета таких вещей, как указанный размер эффекта среди прочего). Если вы позволите эксперименту пройти по намеченному курсу, вы значительно уменьшите свои шансы столкнуться с ошибкой типа 1 (учитывая, что вы используете высокий уровень достоверности). Ожидание получения статистически значимых результатов гарантирует, что вероятность того, что вы ошибочно отклоните нулевую гипотезу и совершите ошибку I рода, очень мала (обычно 5%). Другими словами, используйте хороший размер выборки, потому что это имеет решающее значение для получения статистически значимых результатов.

Теперь это все об ошибках типа I, которые связаны с уровнем уверенности (или значимости) в ваших экспериментах. Но есть и другой тип ошибок, которые могут закрасться в ваши тесты — ошибки типа II.

Понимание ошибок типа II

Ошибки типа II известны как ложноотрицательные или бета-ошибки.

В отличие от ошибки типа I, в случае ошибки типа II эксперимент *КАЖЕТСЯ НЕУСПЕШНЫМ (ИЛИ БЕЗРЕЗУЛЬТАТНЫМ)* , и вы (ошибочно) заключаете, что вариант, который вы тестируете, ничем не отличается от эксперимента. оригинал.

При ошибках типа II вы не видите реальных подъемов или спадов и в конечном итоге не можете отвергнуть нулевую гипотезу и отвергнете альтернативную гипотезу.

Вот как можно совершить ошибку второго рода:

Возвращаясь к тому же сайту B2B сверху…

Итак, предположим, на этот раз вы предполагаете, что добавление заявления об отказе от соблюдения GDPR на видном месте в верхней части вашей формы побудит больше потенциальных клиентов заполнить его (что приведет к большему количеству потенциальных клиентов).

Таким образом, ваша нулевая гипотеза для этого эксперимента выглядит следующим образом: Отказ от ответственности за соответствие GDPR не влияет на заполнение форм.

И альтернативная гипотеза для того же гласит: Отказ от ответственности за соответствие GDPR приводит к большему заполнению форм.

Статистическая мощность теста определяет, насколько хорошо он может обнаруживать различия в производительности вашей исходной версии и версии-претендента, если существуют какие-либо отклонения. Традиционно оптимизаторы стараются достичь отметки статистической мощности в 80%, потому что чем выше этот показатель, тем ниже вероятность совершения ошибок типа II.

Статистическая мощность принимает значение от 0 до 1 (и часто выражается в %) и контролирует вероятность вашей ошибки второго рода (β); рассчитывается как: 1 – β

Чем выше статистическая мощность вашего теста, тем ниже будет вероятность столкнуться с ошибками второго рода.

Таким образом, если эксперимент имеет статистическую мощность 10 %, он может быть весьма восприимчив к ошибке второго рода. Принимая во внимание, что если эксперимент имеет статистическую мощность 80%, вероятность совершения ошибки второго рода будет гораздо меньше.

Вы снова запускаете свой тест, но на этот раз вы не замечаете значительного увеличения числа заполненных форм. Обе версии сообщают о примерно одинаковых конверсиях. Из-за этого вы прекращаете эксперимент и продолжаете использовать исходную версию без заявления об отказе от соблюдения GDPR.

Однако, если вы углубитесь в свои данные о потенциальных клиентах за период эксперимента, вы обнаружите, что, хотя количество потенциальных клиентов в обеих версиях (исходной и альтернативной) кажется одинаковым, версия GDPR действительно дает вам хороший, значительный рост числа лидов из Европы. (Конечно, можно было использовать таргетинг на аудиторию, чтобы показать эксперимент только лидам из Европы — но это уже другая история.)

Здесь произошло то, что вы закончили свой тест слишком рано, не проверив, достигли ли вы достаточной мощности, — совершив ошибку второго рода.

Избегайте ошибок типа II в своих экспериментах

Чтобы избежать ошибок типа II, запускайте тесты с высокой статистической мощностью. Попробуйте настроить свои эксперименты так, чтобы вы могли достичь отметки статистической мощности не менее 80%. Это приемлемый уровень статистической мощности для большинства экспериментов по оптимизации. С его помощью вы можете гарантировать, что по крайней мере в 80% случаев вы правильно отклоните ложную нулевую гипотезу.

Чтобы сделать это, вам нужно посмотреть на факторы, которые добавляют к нему.

Самым большим из них является размер выборки (с учетом наблюдаемого размера эффекта). Размер выборки напрямую зависит от мощности теста. Огромный размер выборки означает высокую мощность теста. Тесты с недостаточной мощностью очень уязвимы для ошибок типа II, поскольку ваши шансы обнаружить различия в результатах вашего претендента и исходных версий значительно снижаются, особенно для низких MEI (подробнее об этом ниже). Таким образом, чтобы избежать ошибок типа II, подождите, пока тест наберет достаточную мощность, чтобы свести к минимуму ошибки типа II. В идеале, в большинстве случаев, вы хотели бы достичь мощности не менее 80%.

Другим фактором является минимальный эффект интереса (MEI) , на который вы ориентируетесь в своем эксперименте. MEI (также называемый MDE) — это минимальная величина разницы, которую вы хотели бы обнаружить в рассматриваемом KPI. Если вы установите низкий MEI (например, ожидая повышения на 1,5%), ваши шансы столкнуться с ошибкой типа II увеличиваются, потому что для обнаружения небольших различий требуются значительно большие размеры выборки (для достижения достаточной мощности).

И, наконец, важно отметить, что существует обратная зависимость между вероятностью совершения ошибки первого рода (α) и вероятностью совершения ошибки второго рода (β). Например, если вы уменьшите значение α, чтобы снизить вероятность совершения ошибки первого рода (скажем, вы установили α равным 1%, что означает доверительный уровень 99%), статистическая мощность вашего эксперимента (или его способность, β , обнаружения разницы, когда она существует) в конечном итоге также уменьшается, тем самым увеличивая вероятность получения ошибки типа II.

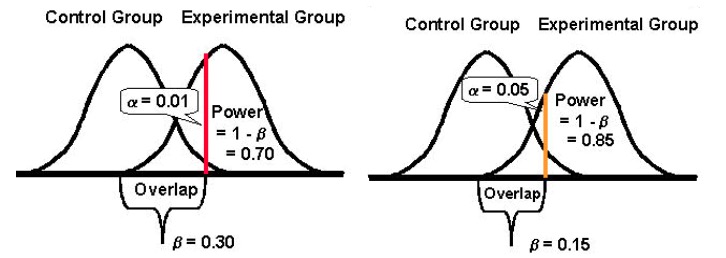
Быть более восприимчивым к любой из ошибок: тип I и II (и найти баланс)

Снижение вероятности одного типа ошибки увеличивает вероятность другого типа (при условии, что все остальное остается прежним).

И поэтому вам нужно решить, к какому типу ошибок вы могли бы быть более терпимы.

С одной стороны, совершение ошибки первого рода и внедрение изменений для всех ваших пользователей может стоить вам конверсий и дохода — что еще хуже, это также может стать убийцей конверсий.

С другой стороны, совершение ошибки типа II и неспособность развернуть выигрышную версию для всех ваших пользователей может, опять же, стоить вам конверсий, которые вы могли бы получить в противном случае.

Неизменно, обе ошибки дорого обходятся.

Однако, в зависимости от вашего эксперимента, один из них может оказаться для вас более приемлемым, чем другой. В целом тестировщики находят ошибку типа I примерно в четыре раза более серьезной, чем ошибку типа II .

Если вы хотите использовать более сбалансированный подход, статистик Джейкоб Коэн предлагает вам выбрать статистическую мощность 80%, которая предполагает «разумный баланс между альфа- и бета-рисками». (мощность 80% также является стандартом для большинства инструментов тестирования.)

А что касается статистической значимости, стандарт установлен на уровне 95%.

По сути, все дело в компромиссе и уровне риска, который вы готовы терпеть. Если вы действительно хотите свести к минимуму вероятность обеих ошибок, вы можете выбрать уровень достоверности 99% и мощность 99%. Но это означало бы, что вы будете работать с невероятно огромными размерами выборки в течение периодов, которые кажутся бесконечно длинными. Кроме того, даже тогда вы оставляете место для ошибок.

Время от времени вы будете заканчивать эксперимент неправильно. Но это часть процесса тестирования — требуется время, чтобы освоить статистику A/B-тестирования. Исследование и повторное тестирование или отслеживание ваших успешных или неудачных экспериментов — это один из способов подтвердить свои выводы или обнаружить, что вы допустили ошибку.