Нормальное распределение — интуитивно понятное введение без математики

Я постараюсь, насколько это возможно, освободить эту статью от уравнений и жаргона. Однако мне нужно, чтобы вы обладали как минимум следующими способностями:

• Умеет интерпретировать простые графики.
• Знание начального уровня вероятности. Вы хоть понимаете, что есть 50% вероятность выпадения орла, если я подброшу монетку.
• Интегральное исчисление и квантовая физика (шучу!)

Почему нормальное распределение

Интуитивный способ понять что-то — исследовать, зачем это нужно. Давайте сделаем это для нормального распределения (также называемого распределением Гаусса).

Скажем, у вас есть забавная привычка. Каждый день вы подбрасываете монету 100 раз. Это «нормально» ожидать, что вы получите голову 50 раз — или почти 50 раз большую часть дня. Редко бывают хорошие дни для головы — вы можете пройти около 55 раз и очень редко больше 65 раз.

Теперь вы хотите количественно оценить эту «редкость». Итак, вы начинаете отслеживать, сколько раз вы получили голову каждый день.

Количество голов каждый день в году

Ниже приведены данные через год (365 дней) — первое — это количество голов, которое вы получили в первый день, а последнее — количество голов, которое вы получили в последний день. Вам не нужно проверять все числа ниже, но легко заметить, что большинство из них около 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Визуализируйте лучше с помощью гистограммы

Давайте построим гистограмму из данных выше:

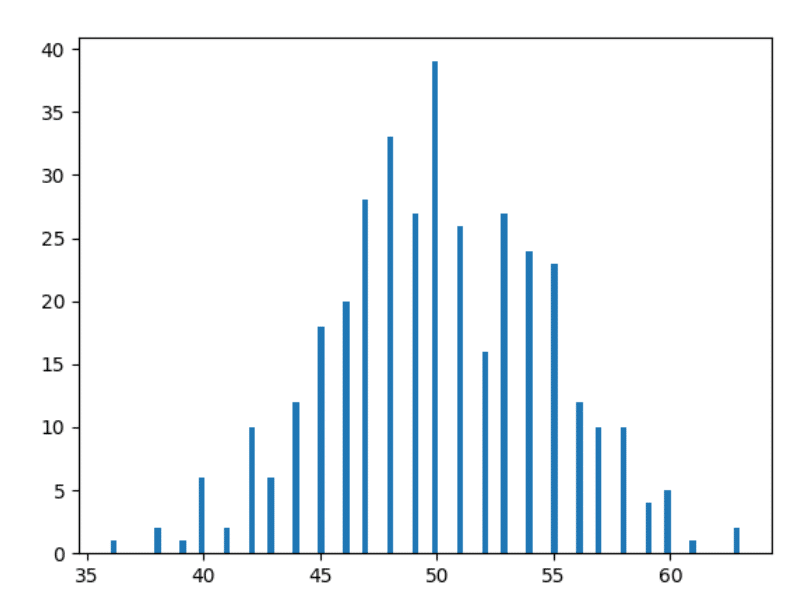
Ага! Разве это уже не похоже на изображение, которое вы видели в Интернете, когда гуглили «Нормальное распространение»? Мы почти на месте!

Итак, если вы не понимаете гистограммы – мы только что отложили здесь количество дней, в течение которых мы получили определенный счет для головы. Например, мы получили голову 36 раз в 2 конкретных дня в году (проверьте данные выше, если не верите мне), поэтому на горизонтальной точке 36 есть полоса высотой 2 единицы (красный цвет). прямоугольник слева на изображении ниже).

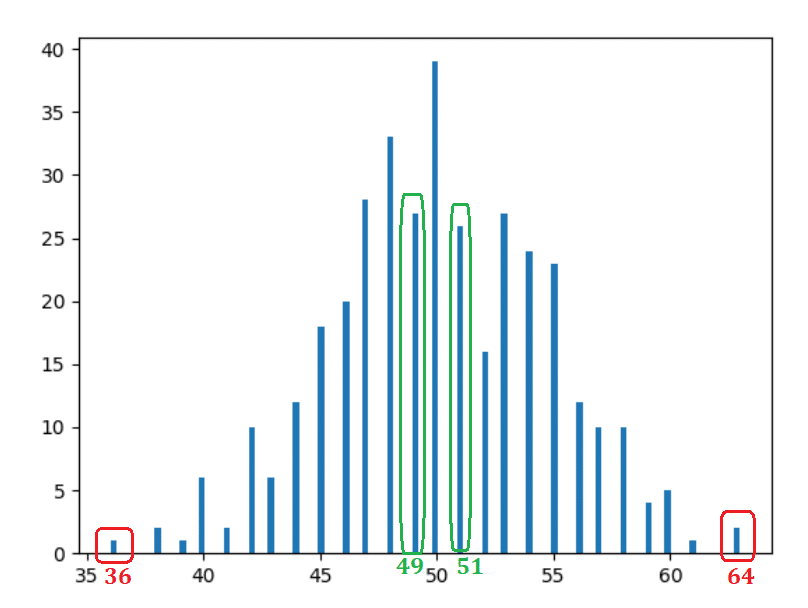
Наблюдения

1. Довольно очевидно и ожидаемо — чаще всего выпадало 50 голов.
2. Чем дальше мы удаляемся от центра (50), тем больше встречаемость уменьшается.
3. Стержни на одинаковом расстоянии принимают одинаковую форму. Например, если вы переместите одну единицу влево (49) или вправо (51) — вхождения будут одинаковыми — 30 и 31 соответственно (зеленые прямоугольники). Если вы переместитесь на 14 единиц влево (36) или вправо (64), вхождения снова будут аналогичны — 2 и 1 соответственно (красные прямоугольники).

данные за 10 лет

Теперь давайте немного перемотаем вперед — и построим данные за 10 лет.

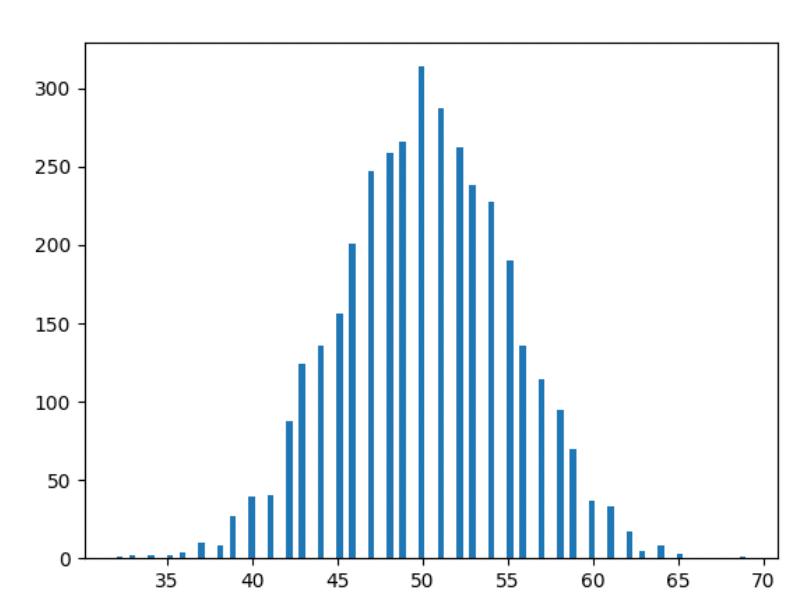
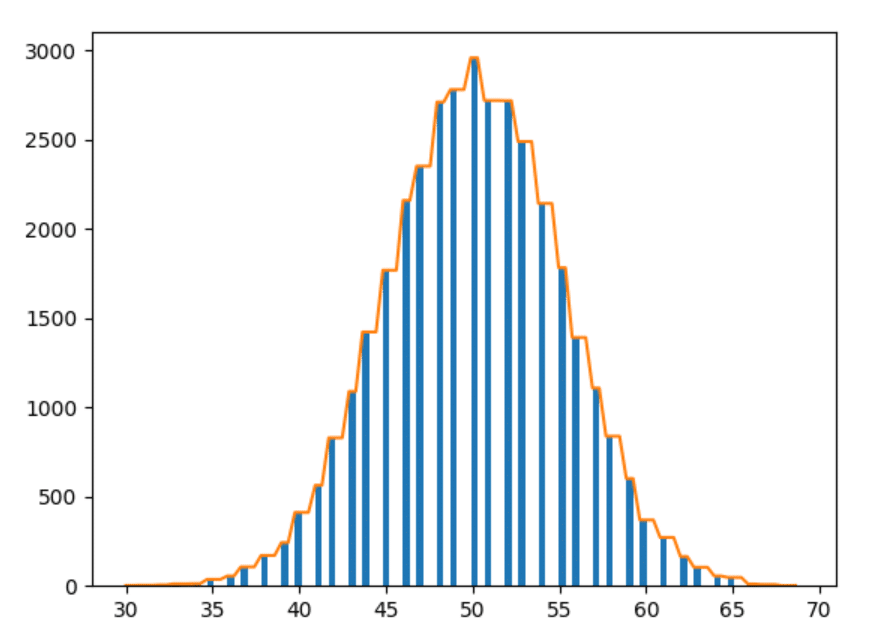
Данные за 1000 лет

Хорошо — последний. Давайте построим данные за 1000 лет.

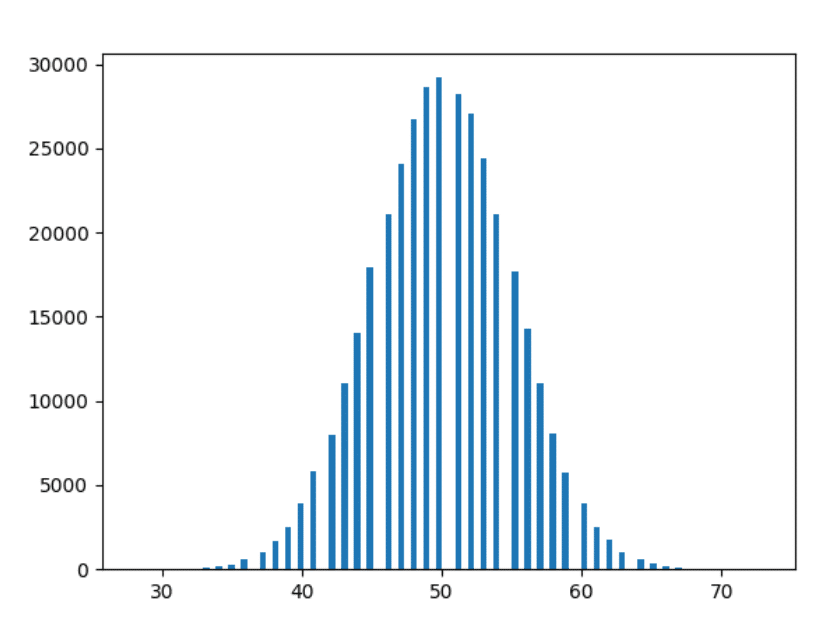
Наблюдения

1. Чем больше мы экспериментируем, тем ровнее получаются формы.
2. Чем больше мы экспериментируем, тем больше столбцы следуют приведенным выше наблюдениям (т.е. столбцы на одинаковом расстоянии принимают более близкую форму).

Где чертово нормальное распределение?

Ладно — слишком много предыстории — теперь давайте перейдем к делу.

Давайте посмотрим на ответ, предложенный Google:

Несколько вещей в этом определении:

Случайная переменная: Проще говоря, случайная величина — это набор возможных значений случайного эксперимента, такого как подбрасывание монеты. В нашем примере возможное значение нашего эксперимента — Голова или Хвост .

В форме колокола: вы заметили, что наша гистограмма принимает форму колокола?

Симметрично: столбики на одинаковом расстоянии имеют одинаковую форму — разве это не симметрично?

Таким образом, нормальное распределение представляет собой распределение результатов для таких событий, как подбрасывание монеты, где распределение имеет тенденцию сохранять несколько свойств, включая симметрию и форму колокола.

Какие явления, кроме подбрасывания монеты, подчиняются нормальному распределению?

Несколько крутых примеров здесь.

• Рост населения — больше людей попадает в группу среднего роста. Редко можно встретить очень высоких или очень низких людей. И шансы найти экстремально высокого и экстремально низкого почти равны.
• Бросание костей
• Размер обуви
• IQ
• И многое другое…

Эти явления строго подчиняются нормальному распределению?

Простой ответ - нет. Хотя, как мы видели выше — чем больше вы экспериментируете, тем больше данные будут следовать свойствам нормального распределения. Но нет никакой гарантии, что какое-то маловероятное событие все равно не произойдет.

Являются ли все распределения вероятностей во Вселенной нормальным распределением?

Нет. Есть много явлений, которые определяются каким-то другим видом распределения.

• Вероятность данного количества прибывающих клиентов, телефонных звонков, несчастных случаев, спортивных мероприятий и наводнений подчиняется распределению Пуассона .
• В бизнес-продажах 20% клиентов компании несут ответственность за 80% продаж. ( Распределение Парето )
• Схемы движения в городе — экспоненциальное распределение
• Случайный выбор членов команды из популяции девочек и мальчиков — гипергеометрическое распределение

И многое другое…

Я составил приведенный выше список, просто погуглив «пример из реальной жизни» с некоторыми перечисленными здесь дистрибутивами — не то, чтобы я понимал их все. 😉

Есть ли причина, по которой некоторые природные явления имеют тенденцию следовать нормальному распределению?

Да — цитирую мое любимое объяснение:

Обычное объяснение дается другим названием нормального распределения — «распределением ошибок». Идея состоит в том, что ошибки, как правило, случайны, так что они с одинаковой вероятностью могут пойти в одном направлении, как и в другом. Например, стрелок может стрелять немного левее, немного правее или чуть выше, чем немного ниже. Таким образом, график того, насколько далеко выстрелы от мишени, будет отражать эту случайную тенденцию и будет симметричен относительно среднего значения. Точно так же с ростом и интеллектом — многие гены (возможно, тысячи) вносят свой вклад в эти результаты, как и большое количество факторов окружающей среды, таких как питание, болезни, низкий доход и так далее.

Параметры нормального распределения

Если у вас есть интуиция обсуждения до сих пор — вы уже победитель. Миссия выполнена. Остальная часть статьи является бонусом.

Все графики нормального распределения, которые вы видите, имеют разную форму. Некоторые из них более плоские, чем другие. Некоторые из них имеют хороший рост. Все эти формы управляются всего двумя параметрами:

Иметь в виду

Среднее значение определяется средним значением. Он определяет высоту колокола. В примере с подбрасыванием монеты среднее значение близко к 50, что является верхним положением на графике.

Стандартное отклонение

Поскольку я обещаю, что в этой статье не будет уравнений, я не буду приводить здесь ее математическое представление. Но в любом случае это не так сложно. Стандартное отклонение — это метрика, показывающая, насколько разнообразны данные.

Например, стандартное отклонение возраста в уходе за детьми будет ниже, чем стандартное отклонение возраста в футбольном фан-клубе, поскольку разница в возрасте между самой младшей и самой старшей группой должна быть намного выше в футбольном фан-клубе.

Стандартное отклонение определяет ширину кривой. Небольшое стандартное отклонение дает крутую кривую, а большее стандартное отклонение дает более пологую кривую.