Почувствуйте исчисление своим чувством программирования

Я верю, что люди, умеющие программировать, способны понимать более сложные понятия, чем исчисление. Одна из причин, почему есть много талантливых программистов, которые все еще борются с исчислением, не в том, что это сложно. Это в основном потому, что нас учили этому неправильно (наряду со многими другими темами).

Если вы хоть раз в жизни занимались программированием — даже с такими игрушечными упражнениями, как генерация простых чисел, — возможно, вы уже занимались подобными вещами, которые происходят в исчислении, но у вас никогда не было возможности рассказать об этом.

Цель этого письма не в том, чтобы научить вас исчислению или программированию, а в том, чтобы помочь вам соединить некоторые точки.

Я перейду к части кодирования через минуту. Но позвольте мне дать некоторую предысторию перед этим.

Скорость изменения

Дифференциальное исчисление говорит о «скорости изменения». Попробуем понять, что это значит.

Для изменения переменной (x) скорость изменения функции равна просто изменению функции, деленному на изменение x. Давайте визуализируем с реальными числами:

Рассмотрим 2 точки x=2 и x=6 и функцию y=f(x) = x².

Также рассмотрим dx = расстояние между этими двумя точками по оси x. А dy — это расстояние между значениями y для этих значений x.

Тогда скорость изменения y от x=2 до x=6 равна

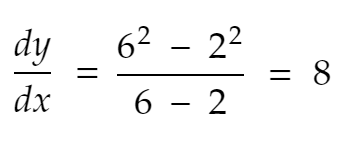
Производная

Теперь — производная dy/dx — это скорость изменения y при бесконечно малом изменении x. Поскольку это расстояние (6–2=4) не бесконечно мало — даже не близко, мы не можем назвать приведенное выше уравнение производной. Итак, давайте пока выберем меньшее число, 0,1 .

Когда x = 0, y = x² = 0² = 0.

Ближайший сосед в положительном направлении, x = 0,1. Там y становится 0,1² = 0,01.

Так,

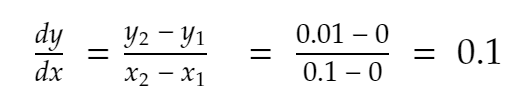
Давайте попробуем еще раз. Ближайший сосед 0,1 в положительном направлении, x = 0,2. Итак, y становится 0,2² = 0,04. Так,

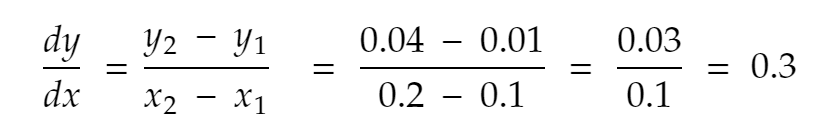
Если мы повторим процесс еще несколько раз, то получим вот что:

Вот файл Excel, если вы хотите поиграть с ним.

dx (которое является нашим вымышленным бесконечно малым расстоянием между двумя соседними точками на оси x) в нашем контексте равно 0,1.

х соответственно увеличивается.

y просто x².

dy — расстояние между двумя соседними значениями y. Например, когда x = 0,1, расстояние между текущим y (0,01) и следующим y (0,04) равно 0,03, поэтому dy равно 0,03 при x = 0,1.

dy/dx — это dy, деленное на dx.

dy/dx / x — это dy/dx, деленное на x.

Теперь обратите внимание, что по мере увеличения x последняя строка приближается к 2, а это означает, что скорость изменения x² по отношению к x приближается к удвоенной величине x, что равно 2x .

Помните производную x² по x? 2 раза! Найти какую-то связь?

Время кодирования

Давайте попробуем в коде то, что мы обсуждали до сих пор.

Предполагая, что у вас уже установлен Python, в терминале запустите:

После этого запустите следующий код Python:

Здесь:

x : содержит числа от 0 до 9.

y : другой массив, каждый элемент которого является квадратом соответствующего элемента x

dy : Другой массив, инициализированный нулями. Мы поместим y-расстояния в этот массив.

dydx : еще один массив, инициализированный нулями. Он будет содержать значение dy/dx для каждой точки.

dx : Довольно очевидно — это размер шага. Расстояние между двумя последовательными числами, которое уменьшается по мере увеличения SIZE. Если РАЗМЕР = 10, dx = 1. Если РАЗМЕР = 100, dx = 0,1.

Во-первых, мы получаем dy для каждой точки. Затем мы вычисляем dydx из него.

Заметь:

Здесь мы опускаем первое и последнее значения. Первое значение x равно 0, что приведет к ошибке деления на ноль. И мы не можем вычислить последнее значение dy/dx, так как у нас нет последнего значения dy — потому что для этого потребуется рядом с последним доступным значением y, которого здесь нет.

Если все пойдет нормально, вы получите такой график:

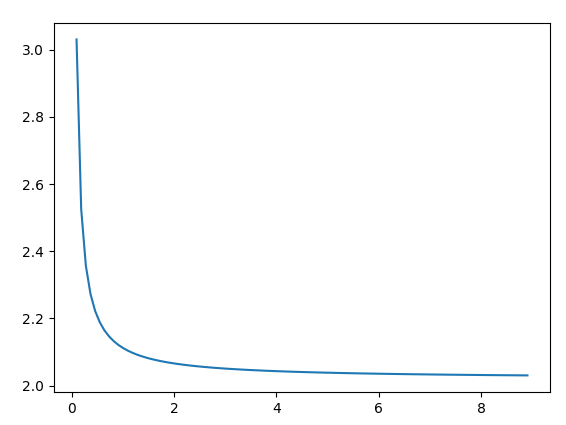
Что вы понимаете из сюжета

Как вы видите, график приближается к 2. Увеличьте значение SIZE (имеется в виду установка меньшего значения dx) и посмотрите, как график быстрее приближается к 2.

Вторая производная

Теперь, когда вы зашли так далеко, осталось сделать еще несколько шагов, чтобы понять вторую производную, которая даст вам интуитивное представление о производной любого порядка.

Как вы помните, вторая производная — это скорость изменения первой производной по x. Проще говоря — dy/dx во второй производной похож на y в первой производной.

Сделаем следующие изменения в приведенном выше коде:

Объявить еще 2 массива:

d2ydx2 : что будет представлять вторую производную:

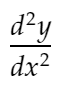
Distance_dydx: для представления расстояния между значением dy/dx между двумя соседними точками.

Вот полный код второй производной:

После вычисления dydx в цикле for мы выполняем еще один цикл для вычисления второй производной. С помощью некоторого мудрого кода мы могли бы вычислить вторую производную в том же цикле (попробуйте в качестве упражнения), но здесь я разделил их для ясности.

Также обратите внимание, что:

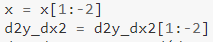
Как и в первой производной, здесь мы опускаем некоторые значения. Последние 2 значения опущены, поскольку для второго из последних потребовалось бы последнее значение «первой производной», которое мы не могли вычислить (поскольку у нас не было требуемого значения y для него — как описано выше). Значит ли это, что мы должны опустить последние 3 значения в случае 3-й производной?🤔 — это вам решать.

Вот выходной график:

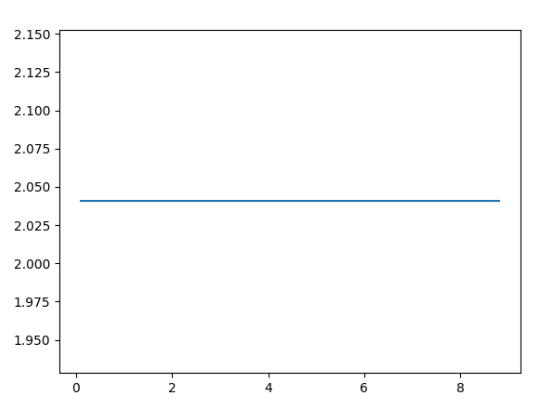
Что мы здесь видим?

Как вы знаете из средней школы:

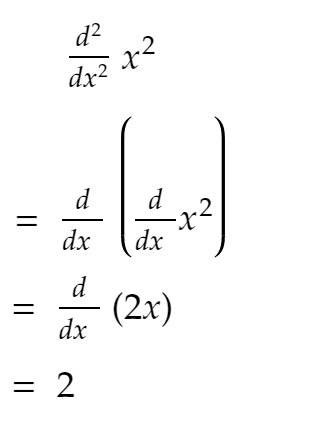
Теперь, как вы видите из кода выше, вторая производная в основном остается постоянной, и если вы продолжаете увеличивать SIZE — она приближается к 2!

Почему важна скорость изменения

Вам может быть интересно:

— Почему мы проходим через все эти неприятные неприятности? Какую полезную информацию мы получаем из скорости изменения или производной?

— Почему мы не можем просто пойти по курсу обмена на любую сумму? Почему только бесконечно мало? Какую информацию мы получаем из скорости изменения по отношению к бесконечно малому , которую нельзя получить из скорости изменения по отношению к большим значениям?

— Эта бесконечно малая штучка чем-то похожа на халтуру? Мы работали с некоторыми небольшими числами выше, но, конечно, не бесконечно малыми.

Если я позволю себе продолжить, вы уйдете, увидев длину этой статьи, и не зайдете так далеко. Возможно, мы ответим на эти вопросы как-нибудь в другой день 😀.