Байесовская статистика: быстрый и простой учебник для A/B-тестеров
Опубликовано: 2022-06-23
Насколько вы уверены в своей способности интерпретировать результаты, полученные с помощью вашего инструмента A/B-тестирования?
Скажем, вы используете инструмент, основанный на байесовской статистике, и он сказал вам, что у «Б» есть 70% шансов победить «А», поэтому «Б» — победитель. Знаете ли вы, что это значит и как это должно повлиять на вашу CRO-стратегию?
В этой статье вы познакомитесь с основами байесовской статистики, которые помогут вам снова контролировать свое A/B-тестирование, в том числе
- Беспристрастный взгляд на байесовскую статистику
- Преимущества и недостатки частотного и байесовского методов
- Подготовка, необходимая для того, чтобы уверенно интерпретировать и использовать результаты байесовского A/B-тестирования, избегая некоторых распространенных ловушек мифов.
- Что такое байесовская статистика?
- Байесовская история происхождения
- Пример применения байесовской статистики к A/B-тестированию
- Краткий глоссарий байесовских терминов, важных для A/B-тестеров
- Байесовский вывод
- Условная возможность
- Распределение вероятностей/распределение правдоподобия
- Предварительное распределение убеждений
- сопряжение
- Сопряженные приоры
- Функция потери
- Что такое статистика частотников?
- Байесовское и частотное A/B-тестирование
- Фреймворк Frequentist
- Байесовская структура
- Что на самом деле говорит байесовская статистика в A/B-тестировании?
- Вероятность стать лучшим (P2BB)
- Ожидаемый рост
- Ожидаемый убыток
- Мифы вокруг байесовской статистики, которых следует избегать
- Миф № 1. Байесовцы заявляют о своих предположениях, а частотисты — нет
- Миф №2. Байесовские методы дают вам ответы, которые вы на самом деле хотите
- Миф № 3: Байесовский вывод помогает вам сообщать о неопределенности лучше, чем частотный вывод
- Миф №4. Результаты байесовского A/B-тестирования защищены от просмотра
- Миф №5. Статистика Frequentist неэффективна, поскольку вы должны ждать фиксированного размера выборки
- Итак, что выбрать: байесовский или частотный? Есть место для обоих.
- Ключевые вынос
Готовый? Начнем с основ.
Что такое байесовская статистика?
Байесовская статистика — это подход к статистическому анализу, основанный на теореме Байеса, которая обновляет представления о событиях по мере сбора новых данных или свидетельств об этих событиях. Здесь вероятность является мерой уверенности в том, что событие произойдет.
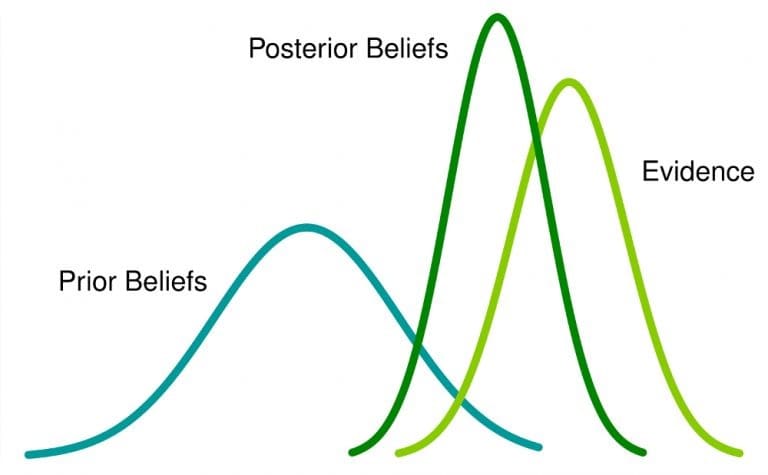
Что это означает: если у вас есть априорное убеждение о событии и вы получаете больше информации, связанной с ним, это убеждение изменится (или, по крайней мере, будет скорректировано) на апостериорное убеждение.
Это полезно для понимания неопределенности или при работе с большим количеством зашумленных данных, например, при оптимизации коэффициента конверсии для электронной коммерции и машинного обучения.
Давайте представим это:
Скажем, например, вы смотрите гонку продуктовых тележек в колледже, а затем возбужденный зритель предлагает вам поспорить, что чувак в красной футболке, возящий даму в зеленой рубашке, выиграет. Вы думаете об этом и возражаете, что вместо этого выиграют парень в черной куртке и девушка в черной толстовке.

Другой зритель над головой прошептал вам подсказку: «Парень в красной футболке выиграл последние 3 гонки из 4». Что происходит с вашей ставкой? Ты уже не слишком уверен, верно?
Предположим, вы также узнали, что в последний раз, когда парень в черной куртке надевал свои счастливые солнцезащитные очки, он выиграл. И когда он не надевал ее, выигрывал парень в красной футболке.
Сегодня вы видите, что парень в черной куртке носит эти очки. Ваша вера снова меняется. Теперь ты больше веришь в свою ставку, верно? В этой истории вы обновляли свое убеждение каждый раз, когда получали доказательства новых данных. Это байесовский подход.
Байесовская история происхождения
Когда преподобный Томас Байес впервые подумал о своей теории, он не подумал, что она достойна публикации. Таким образом, он оставался в его записях более десяти лет. Когда его семья попросила Ричарда Прайса просмотреть его записи, Прайс обнаружил записи, которые легли в основу теоремы Байеса.
Все началось с мысленного эксперимента Байеса. Он подумал о том, чтобы сесть спиной к идеально плоскому квадратному столу и попросить ассистента бросить мяч на стол.
Мяч мог приземлиться где угодно на столе, но Байес думал, что сможет догадаться, где именно, обновляя свои догадки новой информацией. Когда мяч приземлялся на стол, он просил ассистента сказать ему, приземлился ли он слева или справа, впереди или позади того места, где приземлился предыдущий мяч.
Он заметил это и стал слушать, как на стол приземляются новые шары. С такой дополнительной информацией он обнаружил, что может повышать точность своих догадок с каждым броском. Это привело к идее обновления нашего понимания по мере того, как мы получали больше данных из наблюдений.
Байесовский подход к анализу данных применяется в различных областях, таких как наука и инженерия, и даже включает спорт и право.
В рандомизированных контролируемых онлайн-экспериментах, в частности в A/B-тестировании, вы можете использовать байесовский подход, состоящий из 4 шагов:
- Определите свое предыдущее распределение.
- Выберите статистическую модель, которая отражает ваши убеждения.
- Проведите эксперимент.
- После наблюдения обновите свои убеждения и рассчитайте апостериорное распределение.
Вы обновляете свои убеждения, используя набор правил, называемый байесовским алгоритмом.
Пример применения байесовской статистики к A/B-тестированию
Давайте проиллюстрируем пример байесовского A/B-тестирования.
Представьте, что мы провели простой A/B-тест кнопки CTA в магазине Shopify. Для «А» мы используем «Добавить в корзину», а для «Б» мы используем «Добавить в корзину».
Вот как частотник подойдет к тесту.
Есть два альтернативных мира: один, где A и B не отличаются друг от друга, поэтому тест не покажет никакой разницы в коэффициенте конверсии. Это нулевая гипотеза. А в другом мире есть разница, так что одна кнопка будет работать лучше, чем другая.
Частотист предположит, что мы живем в мире 1, где нет никакой разницы в кнопках CTA, то есть предположим, что нулевая гипотеза верна. А затем они попытаются доказать, что это не так, с заранее установленным уровнем уверенности, называемым уровнем значимости.
Но вот как байесовец подойдет к тому же тесту:
Они начинают с априорного убеждения, что обе кнопки A и B имеют равные шансы обеспечить коэффициент конверсии от 0 до 100%. Таким образом, есть равенство кнопок прямо из ворот — у обоих есть 50% шанс стать лучшими.
Затем начинается тест и собираются данные. Наблюдая за новой информацией, байесовские A/B-тестеры будут обновлять свои знания. Таким образом, если B подает надежды, они могут прийти к апостериорному убеждению, основанному на этом наблюдении, в котором говорится: «B имеет 61%-й шанс победить A».
Между этими двумя методами есть принципиальные различия.
Вот почему для нас важно придерживаться беспристрастного подхода к байесовскому A/B-тестированию.
Большинство байесовских инструментов A/B-тестирования — возможно, в маркетинговых целях — занимают крайнюю античастотную позицию и выдвигают аргумент, что байесовский анализ лучше подсказывает, какой вариант более «прибыльный».
Но обладает ли какой-либо отдельный статистический подход к A/B-тестированию исключительными правами на выводы?
Если продолжить байесовский аргумент, можно столкнуться с исследованиями, в которых респонденты говорят, что хотят знать, как лучше поступить, или хотят максимизировать прибыль, или что-то подобное. Это твердо ставит вопрос на территорию теории принятия решений — то, в чем ни байесовский вывод, ни частотный вывод не могут иметь прямого значения.
Георги Георгиев, создатель Analytics-toolkit.com и автор книги «Статистические методы в онлайн-тестировании A/B».
Мы кратко рассмотрим эти детали в следующих разделах. А пока давайте сделаем остальную часть этого учебника легкой для понимания.
Краткий глоссарий байесовских терминов, важных для A/B-тестеров
Байесовский вывод
Байесовский вывод обновляет вероятность гипотезы новыми данными. Он построен вокруг убеждений и вероятностей.
Байесовский вывод использует условную вероятность, чтобы помочь нам понять, как данные влияют на наши убеждения. Допустим, мы начинаем с априорного убеждения, что небо красное. Посмотрев на некоторые данные, мы вскоре поймем, что это предыдущее убеждение неверно. Итак, мы выполняем байесовское обновление, чтобы улучшить нашу неверную модель цвета неба, в результате чего получаем более точное апостериорное убеждение .
Майкл Берк в книге «На пути к науке о данных»
Условная возможность
Условная вероятность — это вероятность события при условии, что произошло другое событие. То есть вероятность А при условии В.
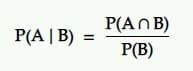
Перевод: Вероятность того, что событие А произойдет при наличии другого события В, равна вероятности того, что В и А произойдут вместе, деленной на вероятность события В.
Распределение вероятностей/распределение правдоподобия
Распределения правдоподобия — это распределения, которые показывают, насколько вероятно, что ваши данные примут определенное значение.
Если ваши данные могут принимать несколько значений, например, такие категории, как цвета, которые могут быть серыми, красными, оранжевыми, синими и т. д., ваше распределение является полиномиальным. Для набора чисел распределение может быть нормальным. А для значений данных, которые могут быть либо да/нет, либо истина/ложь, они будут биномиальными.
Предварительное распределение убеждений
Или априорное распределение вероятностей, просто называемое априорным, выражает ваше убеждение до того, как вы получили доказательства новых данных. Итак, это выражение вашего первоначального убеждения, которое вы собираетесь обновить после рассмотрения некоторых доказательств с использованием байесовского анализа (или вывода).
сопряжение
Прежде всего, конъюгат относится к соединению вместе, обычно попарно. В байесовской теории вероятности сопряженность предполагает, что априор сопряжен с вероятностью.
Если апостериорная функция имеет ту же функциональную форму, что и априорная, то априорная функция сопряжена с функцией правдоподобия. Это показывает, как функция правдоподобия обновляет предыдущее распределение.
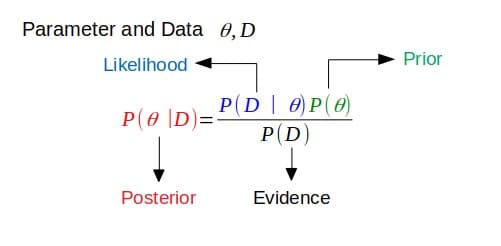
Сопряженные приоры
Это связано с приведенным выше определением. Если апостериорное распределение находится в том же семействе распределения вероятностей (или имеет ту же функциональную форму), что и априорное распределение вероятностей, то априорное и апостериорное распределения являются сопряженными распределениями. В этом случае априор называется сопряженным априором для функции правдоподобия.
Они могут быть субъективными (основанными на знаниях экспериментатора), объективными и информативными (основанными на исторических данных) или неинформативными.
Функция потери
Функция потерь — это способ количественной оценки потерь путем измерения того, насколько плоха наша текущая оценка. Это помогает нам свести к минимуму потери при проверке гипотез, особенно при выражении вывода, лежащего в диапазоне вероятных значений, и поддерживать принятие решений с помощью результатов наших испытаний.
Теперь с этим покончено, мы можем двигаться дальше.
Если вы какое-то время были в этом квартале, вы, вероятно, сталкивались с более чем несколькими мемами Frequentist vs Bayesian Statistics.

Обе стороны, похоже, ищут ответы с противоположных сторон, но так ли это на самом деле? Чтобы лучше понять это (оставаясь при этом беспристрастным), давайте посетим лагерь Frequentists.
Что такое статистика частотников?
Это первый метод логического вывода, который большинство людей изучают в статистике. Частотная статистика вычисляет вероятность того, что событие (гипотеза) происходит часто при одних и тех же условиях.
Проверка гипотез A/B с использованием частотного подхода состоит из следующих шагов:
- Сформулируйте несколько гипотез. Как правило, нулевая гипотеза состоит в том, что новый вариант «В» не лучше исходного «А», тогда как альтернативная гипотеза утверждает обратное.
- Заранее определите размер выборки с помощью статистического расчета мощности , если только вы не используете методы последовательного тестирования. Используйте калькулятор размера выборки, который учитывает статистическую мощность, текущий коэффициент конверсии и минимальный обнаруживаемый эффект.
- Запустите тест и подождите, пока каждый вариант будет представлен заранее определенному размеру выборки.
- Рассчитайте вероятность наблюдения результата, по крайней мере столь же экстремального, как данные при нулевой гипотезе (p-значение). Отклоните нулевую гипотезу и разверните новый вариант в производстве, если p-значение < 5%.
Как это соотносится с байесовским? Посмотрим…
Байесовское и частотное A/B-тестирование
Это печально известная дискуссия везде, где используется статистический вывод. А если быть откровенным, то бессмысленно. У обоих есть свои достоинства и случаи, когда они являются лучшим методом для использования.
Вопреки тому, что большинство промоутеров из обоих лагерей заставят вас думать, они во многом похожи, и ни один из них не ближе к истине, чем другой, хотя их подходы различаются.
Например, применительно к A/B-тестированию ни один конкретный метод не даст вам абсолютного и точного прогноза относительно курса действий, который приведет к росту бизнеса. Вместо этого A/B-тестирование помогает вам исключить риск из процесса принятия решений.
Независимо от того, как вы анализируете свои данные — с помощью байесовского или частотного подходов — вы можете делать ходы с определенной степенью уверенности в своей правоте.
И по этой причине обе статистические модели действительны. Байесовский метод может иметь преимущество в скорости, но требует больше вычислительных ресурсов, чем частотный.
Ознакомьтесь с другими отличиями…
Фреймворк Frequentist
Большинство из нас знакомы с частотным подходом из вводных курсов по статистике. Мы определили методологию выше — от объявления нулевой гипотезы, определения размера выборки, сбора данных с помощью рандомизированного эксперимента и, наконец, наблюдения за статистически значимым результатом.
В фреквентизме мы рассматриваем вероятность как фундаментально связанную с частотой повторяющихся событий. Таким образом, при правильном подбрасывании монеты частый игрок полагает, что если он будет угадывать достаточно часто, то в 50% случаев упадет орел и то же самое в случае решки.
Фреквентистское мышление: «Если я буду повторять эксперимент в одних и тех же условиях снова и снова, каковы шансы, что мой метод даст правильный ответ?»
Байесовская структура
В то время как частотный подход рассматривает параметр совокупности для каждого варианта как (неизвестную) константу, байесовский подход моделирует каждое значение параметра как случайную величину с некоторым распределением вероятностей.
Здесь вы вычисляете распределения вероятностей (и, следовательно, ожидаемые значения) для интересующих параметров напрямую.
И чтобы смоделировать распределение вероятностей для каждого варианта, мы полагаемся на правило Байеса, чтобы объединить результаты эксперимента с любыми имеющимися у нас предварительными знаниями об интересующей метрике. Мы можем упростить вычисления, используя сопряженный априор.
Алекс Биркетт резюмировал байесовский алгоритм следующим образом:
- Определите предварительное распределение, которое включает ваши субъективные представления о параметре. Априор может быть неинформативным или информативным.
- Соберите данные.
- Обновите свое предыдущее распределение данными, используя теорему Байеса (хотя вы можете использовать байесовские методы без явного использования правила Байеса — см. Непараметрический байесовский метод), чтобы получить апостериорное распределение. Апостериорное распределение — это распределение вероятностей, которое представляет ваши обновленные представления о параметре после просмотра данных.
- Проанализируйте апостериорное распределение и суммируйте его (среднее, медиана, стандартное отклонение, квантили…).
Короче говоря, байесовский экспериментатор сосредотачивается на своей собственной точке зрения и на том, что для него значит вероятность. Их мнение развивается вместе с наблюдаемыми данными. Часто задаваемые вопросы, с другой стороны, считают, что правильный ответ где-то там.

Поймите, что дебаты Frequentist и Bayesian не так уж сильно влияют на анализ после A/B-тестирования. Основные различия между двумя лагерями больше связаны с тем, что можно проверить.
Вероятностная статистика, как правило, мало используется в последующем анализе. Аргумент байесовско-частотного анализа более применим в отношении выбора переменных для тестирования в парадигме A/B, но даже в этом случае большинство тестировщиков A/B нарушают до чертиков исследовательские гипотезы, вероятности и доверительные интервалы .
Доктор Роб Балон в CXL
Далее Георгий уточняет:
Существует множество байесовских онлайн-калькуляторов и по крайней мере один крупный поставщик программного обеспечения для A/B-тестирования, применяющий байесовский статистический движок, и все они используют так называемые неинформативные априорные значения (немного неправильное название, но давайте не будем углубляться в это). В большинстве случаев результаты этих инструментов численно совпадают с результатами частотного теста на тех же данных. Допустим, байесовский инструмент сообщит что-то вроде «вероятность 96%, что B лучше, чем A», в то время как частотный инструмент выдаст значение p, равное 0,04, что соответствует уровню достоверности 96%.
В ситуации, подобной приведенной выше, которая встречается гораздо чаще, чем некоторые хотели бы признать, оба метода приведут к одному и тому же выводу, а уровень неопределенности будет одинаковым, даже если интерпретация различна.
Что сказал бы байесовец об этом результате? Превращает ли это p-значение в правильную апостериорную вероятность при просмотре сценария, в котором нет априорной информации? Или все эти применения байесовских тестов ошибочны из-за использования неинформативного априора как такового?
На самом деле нет необходимости выбирать лагерь и находить место за укрытием, чтобы бросать камни в другой лагерь. Есть даже свидетельства того, что обе платформы дают одинаковые результаты. Независимо от того, какую дорогу вы выберете, пункт назначения, вероятно, будет одним и тем же. Это зависит от того, как вы сможете добиться этого с помощью Frequentist против Bayesian.
Например:
- Есть данные, показывающие, что байесовское тестирование быстрее и предпочтительнее для интерактивных экспериментов:
Поскольку байесовская парадигма позволяет экспериментаторам формально оценивать убеждения и включать дополнительные знания, она выполняется быстрее, чем традиционный статистический анализ.
В моделировании байесовского A/B-тестирования, когда критерий принятия решения был скорректирован (т. е. увеличена устойчивость к ошибкам), 75% экспериментов завершились в пределах 22,7% наблюдений, требуемых традиционным подходом (при уровне значимости 5%). И он зафиксировал только 10% ошибок типа II. - Байесовцы также считаются более снисходительными, в то время как частотники не склонны к риску:
В то время как многие тесты Frequentist используют статистическую значимость 95%, байесовцы могут довольствоваться меньшим значением. Если у варианта есть 78% шанс превзойти контроль, в зависимости от ожидаемых потерь, может быть разумным решением развернуть этот вариант.
Если вы ошибаетесь и ожидаемый убыток составляет менее процента, это довольно незначительный ущерб для многих предприятий. Этот отрывочный подход может лучше подходить для быстрого принятия решений в сценариях с очень низким уровнем риска. - Однако байесовское моделирование и расчеты требуют больших вычислительных ресурсов:
Frequentist, с другой стороны, основан на ручке и бумаге. Предупреждение: если ваш инструмент A/B-тестирования использует байесовский подход, и вы не знаете, какие допущения добавляются к вашим данным, то вы не можете полагаться на «ответ», который дает вам ваш поставщик. Возьмите его с щепоткой соли. И проведите собственный анализ.
С байесовским подходом не все так радужно и солнечно. Как указывает Георгий с этим списком вопросов:
- «Вы хотите получить произведение априорной вероятности и функции правдоподобия?»
- «Хотите на выходе смесь априорных вероятностей и данных?»
- «Вы хотите, чтобы субъективные убеждения, смешанные с данными, давали результат?» (при использовании информативных априоров)
- «Не могли бы вы представить статистику, в которой априорная информация, которая считается весьма достоверной, смешана с фактическими данными?»
Это все аспекты байесовской статистики, если говорить простым языком.
Что на самом деле говорит байесовская статистика в A/B-тестировании?
Вы разработали A/B-тест, чтобы понять, как изменение влияет на интересующую вас метрику, например на коэффициент конверсии или доход на одного посетителя.
Когда вы используете инструмент, работающий с байесовской статистикой, важно понимать, что означают ваши результаты, поскольку фраза «Б — победитель» не означает в точности то, что думает большинство людей.
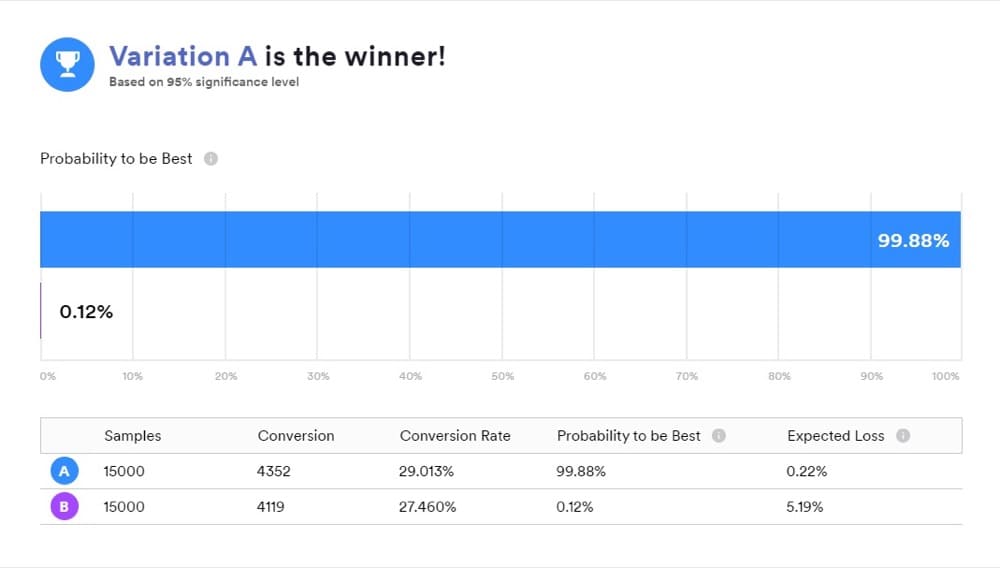
Это удобный способ представить результаты, но это не то, что показал ваш тест. Вместо этого ответы, которые вам нужны, находятся в апостериорных сравнениях «А» и «Б».
Вот 3 метода сравнения:
Вероятность стать лучшим (P2BB)
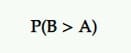
Это вероятность, которая объявляет победителя в байесовском A/B-тестировании.
Вариант с вероятностью быть лучшим — это вариант с наибольшей вероятностью продолжать превосходить другой.
Это вычисляется из набора апостериорных выборок интересующей меры от оригинала и претендента.
Так, например, если B имеет наибольшую вероятность увеличения коэффициента конверсии, B объявляется победителем.
Ожидаемый рост
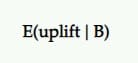
Итак, если B является победителем, какой прирост мы можем ожидать от него? Будет ли он продолжать давать те же результаты, которые мы видели в тесте?
Это понимание ожидаемого подъема стремится обеспечить. Ожидаемый выигрыш от выбора B вместо A с учетом набора апостериорных выборок определяется как достоверный интервал (или среднее значение) процентного увеличения.
В A/B-тестировании мы обычно сравниваем это как претендент с контролем. Таким образом, если претендент проиграл, он представлен отрицательными значениями (например, -11,35%) и положительными значениями (например, +9,58%), если он выиграл.
Ожидаемый убыток
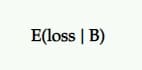
Поскольку нет 100%-ной вероятности того, что B лучше, чем A, то есть шанс записать убыток, если вы выберете B, а не A. Это представлено как ожидаемый убыток и, как и в случае с ожидаемым подъемом, выражается из точка зрения претендента против контроля.
Он сообщает вам о риске выбора вашего варианта P2BB (т. е. объявленного победителя).
Прежде чем мы погрузимся в мифы, огромное спасибо легенде аналитики Георгию Георгиеву. Его глубокий анализ частотного и байесовского вывода, а также байесовской вероятности и статистики в A/B-тестировании вдохновил его на создание следующего раздела.
Мифы вокруг байесовской статистики, которых следует избегать
С соперничеством, которое столь же старо, сколь и бесполезно, дебаты между байесовцами и частотниками собрали много информации и породили множество мифов.
Самый большой из этих мифов (миф № 2) продвигается поставщиками инструментов A/B-тестирования, чтобы рассказать вам, почему один подход лучше другого.
Но после прочтения разделов выше вы знаете лучше.
Давайте раскроем дыры в этих мифах.
Миф № 1. Байесовцы заявляют о своих предположениях, а частотисты — нет
Это говорит о том, что байесовцы делают предположения в форме априорных распределений, и они открыты для оценки. Но Frequentists делают предположения, которые скрыты в середине математики.
Почему это неправильно: байесовцы и частотщики делают одинаковые базовые предположения, единственная разница в том, что байесовцы делают дополнительные предположения — поверх математики.
Частотные модели используют предположения в математике, такие как форма распределения, однородность или неоднородность эффекта по наблюдениям и независимость наблюдения. И они не скрыты. Фактически, они широко обсуждаются в статистическом сообществе и устанавливаются для каждого частотного статистического теста.
Правда: частотщики явно формулируют свои предположения и делают еще один шаг, чтобы проверить предположения: тесты на нормальность, тест на согласие (в соответствии с которым у нас есть тест на несоответствие отношения выборки) и многое другое.
Миф №2. Байесовские методы дают вам ответы, которые вы на самом деле хотите
Заблуждение здесь состоит в том, что p-значения и доверительные интервалы не говорят тестерам то, что они хотят знать, в то время как апостериорные вероятности и достоверные интервалы говорят. Люди хотят знать такие вещи, как
- Вероятность того, что B превзойдет A и
- Вероятность того, что результат не является случайным.
P-значения и проверки гипотез (прямой вывод) не предоставляют эту информацию, но дает обратный вывод.
Почему это неправильно: это вопрос лингвистики. Как правило, когда специалисты, не занимающиеся статистикой, используют такие термины, как «вероятность», «шанс» и «вероятность», они не учитывают их технического значения. Копните глубже, и вы обнаружите, что они так же запутались в обратном выводе, как и в прямом.
По словам Георгия Георгиева, начинают появляться такие вопросы:
- « Что такое априорная вероятность? Какую ценность это приносит?»
- «Что такое функция правдоподобия?»
- «Какая «априорная» вероятность, у меня нет априорных данных?»
- «Как мне защитить выбор априорной вероятности?»
- «Есть ли способ передать только то, что говорят данные, без каких-либо этих смесей?»
Правда: должно быть лучше понимание того, что хотят знать тестировщики, а не их неправильное толкование технических терминов. P-значения, доверительные интервалы и другие параметры сообщают вам, насколько хорошо изучены результаты собранных данных. Они обеспечили меру уверенности без влияния субъективных, непроверенных предварительных предположений.
Миф № 3: Байесовский вывод помогает вам сообщать о неопределенности лучше, чем частотный вывод
Потому что результаты тестов дают более «значимые» выводы.
Почему это неправильно: и частотный, и байесовский подходы имеют схожие инструменты, помогающие сообщить уверенность и результаты вашего A/B-теста.
| частост | байесовский | ||||||||||
| ● Точечные оценки | ● Точечные оценки | ||||||||||
| ● Р-значения | ● Достоверные интервалы | ||||||||||
| ● Доверительные интервалы | ● Факторы Байеса | ||||||||||
| ● Кривые P-значения | ● Апостериорные распределения (выполнить ту же задачу как кривые Frequentist) | ||||||||||
| ● Кривые достоверности | |||||||||||
| ● Кривые серьезности и т. д. |
Правда: все зависит от того, как вы их используете. Оба метода одинаково эффективны в сообщении о неопределенности. Однако существуют различия в том, как они представляют меру неопределенности.
Миф №4. Результаты байесовского A/B-тестирования защищены от просмотра
Некоторые байесовские статистики утверждают, что «вы можете остановить байесовский тест, как только увидите «явного победителя», и это мало повлияет на конечный результат.
Вы, наверное, знаете, что это неприемлемо в частотных тестах, поэтому считается недостатком по сравнению с байесовским. Но так ли это на самом деле?
Почему это неправильно: в исследовании 1969 г., опубликованном в Журнале Королевского статистического общества под названием «Повторные тесты значимости накопленных данных», Armitage et al. показали, как необязательная остановка на основе результата увеличивает вероятность ошибки.
Вы не можете просто остановиться, когда заметите победителя, обновить свой апостериор и использовать его в качестве следующего априорного, не изменив способ работы байесовского анализа.
Правда: Подглядывание влияет на байесовский вывод так же сильно, как и на Frequentist (если вы хотите сделать это правильно).
Миф №5. Статистика Frequentist неэффективна, поскольку вы должны ждать фиксированного размера выборки
Некоторые члены сообщества CRO считают, что частотные статистические тесты должны выполняться с фиксированным, заранее определенным размером выборки, иначе результаты будут недействительными.
В результате вы ждете дольше, чем необходимо, чтобы получить желаемые результаты.
Почему это неправильно: статистика Frequentist не использовалась таким образом уже около семи десятилетий. При частотных последовательных тестах вам не требуется фиксированная заранее определенная продолжительность.
Правда: последовательные тесты, которые сегодня более популярны, требуют максимального размера выборки, чтобы сбалансировать ошибки типа I и типа II, но фактический размер используемой выборки варьируется от случая к случаю в зависимости от наблюдаемого результата.
Итак, что выбрать: байесовский или частотный? Есть место для обоих.
Нет необходимости выбирать сторону. Оба метода имеют свое место. Например, долгосрочный проект, который использует обновленные априорные данные и нуждается в быстрых результатах, лучше подходит для байесовского подхода.
С другой стороны, метод Frequentist лучше всего подходит для проектов, требующих значительной повторяемости результатов. Например, при написании программного обеспечения, которое будут использовать многие люди с большим количеством наборов данных.
Как говорит Кэсси Козырков, глава отдела анализа решений в Google, «статистика — это наука о том, как менять свое мнение в условиях неопределенности».
В своем сводном видео по байесовской и частотной статистике она сказала:
«Вы можете взять дискуссию между частотниками и байесовцами и свести все к тому, о чем вы меняете свое мнение. Частые меняют свое мнение о действиях, у них есть предпочтительное действие по умолчанию — может быть, у них нет никаких убеждений — но у них есть действие, которое им нравится в неведении, а затем они спрашивают: «Изменяют ли мои доказательства [или данные] мое мнение о это действие?» «Чувствую ли я себя нелепо, делая это, основываясь на моих доказательствах?»
С другой стороны, байесовцы меняют свое мнение по-другому. Они начинают с мнения, математически выраженного личного мнения, называемого априорным, а затем спрашивают: «Какое разумное мнение у меня должно быть после того, как я приведу некоторые доказательства?» И поэтому фреквентисты меняют свое мнение о действиях, байесовцы меняют свое мнение об убеждениях.
И в зависимости от того, как вы хотите сформулировать свое решение, вы можете предпочесть один лагерь, а не другой».
В конце концов, мы все приходим к одним и тем же выводам — разница в том, как эти выводы вам преподносят.
Если бы частотный и байесовский вывод были функциями программирования, а входные данные представляли бы собой статистические задачи, то они бы различались тем, что они возвращают пользователю. Функция частотного вывода будет возвращать число, представляющее оценку (обычно сводную статистику, такую как среднее значение выборки и т. д.), тогда как байесовская функция будет возвращать вероятности.
Отрывок из книги «Вероятностное программирование и байесовские методы для хакеров».
Что не совсем правильно, так это утверждение, что одно дает больше практических результатов, чем другое.
Ключевые вынос
Байесовская статистика в A/B-тестировании состоит из 4 отдельных шагов:
- Определите свое предыдущее распределение
- Выберите статистическую модель, которая отражает ваши убеждения
- Проведите эксперимент
- Используйте результаты, чтобы обновить свои убеждения и рассчитать апостериорное распределение.
Ваши результаты укажут вам на проницательные вероятности. Таким образом, вы будете знать, какой вариант с наибольшей вероятностью будет лучшим, ожидаемый убыток и ожидаемый рост.
Обычно они интерпретируются для вас большинством инструментов A/B-тестирования с использованием байесовской статистики. Но тщательный экспериментатор выполнит посттестовый анализ, чтобы лучше понять эти результаты.
Поскольку вы зашли так далеко, вот вам забавный факт: вы знаете портрет Томаса Байеса, с которым все знакомы? Вот этот:

Никто на 100% не уверен, что это он.