Erori de tip I și de tip II: erori inevitabile în optimizare

Erorile de tip I și de tip II apar atunci când identificați în mod eronat câștigătorii în experimentele dvs. sau nu reușiți să îi identificați. Cu ambele erori, ajungi să mergi cu ceea ce pare să funcționeze sau nu. Și nu cu rezultatele reale.

Interpretarea greșită a rezultatelor testelor nu are ca rezultat doar eforturi de optimizare greșite, ci poate, de asemenea, să vă deraieze programul de optimizare pe termen lung.

Cel mai bun moment pentru a detecta aceste erori este chiar înainte de a le face! Deci, să vedem cum puteți evita să întâlniți erori de tip I și de tip II în experimentele dvs. de optimizare.

Dar înainte de asta, să ne uităm la ipoteza nulă... deoarece respingerea sau nerespingerea eronată a ipotezei nule provoacă erori de tip I și de tip II .

Ipoteza nulă: H0

Când formulați ipoteza unui experiment, nu săriți direct pentru a sugera că modificarea propusă va muta o anumită valoare.

Începeți prin a spune că modificarea propusă nu va afecta deloc valoarea în cauză - că nu au nicio legătură.

Aceasta este ipoteza ta nulă (H0). H0 este întotdeauna că nu există nicio schimbare. Aceasta este ceea ce crezi, implicit... până când (și dacă) experimentul tău îl respinge.

Și ipoteza ta alternativă (Ha sau H1) este că există o schimbare pozitivă. H0 și Ha sunt întotdeauna opuse matematice. Ha este cea în care vă așteptați ca schimbarea propusă să facă o diferență, este ipoteza dvs. alternativă - și asta este ceea ce testați cu experimentul dvs.

Deci, de exemplu, dacă doriți să desfășurați un experiment pe pagina dvs. de prețuri și să adăugați o altă metodă de plată la acesta, mai întâi ați forma o ipoteză nulă care să spună: metoda de plată suplimentară nu va avea niciun impact asupra vânzărilor. Ipoteza dvs. alternativă ar fi: Metoda de plată suplimentară VA crește vânzările.

Derularea unui experiment înseamnă, de fapt, contestarea ipotezei nule sau a status quo-ului.

Erorile de tip I și de tip II apar atunci când respingi sau nu respingi în mod eronat ipoteza nulă.

Înțelegerea erorilor de tip I

Erorile de tip I sunt cunoscute ca false pozitive sau erori Alpha.

Într-un exemplu de eroare de tip I de testare a ipotezelor, testul sau experimentul dvs. de optimizare * PARE A FI REUSIT* și (în mod eronat) ajungeți la concluzia că variația pe care o testați se descurcă diferit (mai bine sau mai rău) decât cea originală.

În erorile de tip I, vedeți creșteri sau scăderi - care sunt doar temporare și probabil că nu se vor menține pe termen lung - și ajungeți să vă respingeți ipoteza nulă (și să vă acceptați ipoteza alternativă).

Respingerea eronată a ipotezei nule se poate întâmpla din diverse motive, dar principalul este acela al practicii de peeking (adică, privind rezultatele dvs. între timp sau când experimentul este încă în desfășurare). Și apelarea testelor mai devreme decât este atins criteriul de oprire stabilit.

Multe metodologii de testare descurajează practica analizei, deoarece analiza rezultatelor intermediare ar putea duce la concluzii greșite, care ar duce la erori de tip I.

Iată cum ați putea face o eroare de tip I:

Să presupunem că optimizați pagina de destinație a site-ului dvs. B2B și presupuneți că adăugarea de insigne sau premii la aceasta va reduce anxietatea potențialilor dvs., crescând astfel rata de completare a formularelor (rezultând mai mulți clienți potențiali).

Prin urmare, ipoteza dvs. nulă pentru acest experiment devine: Adăugarea de insigne nu are niciun impact asupra completărilor formularelor.

Criteriul de oprire pentru un astfel de experiment este de obicei o anumită perioadă și/sau după ce conversiile X au loc la nivelul de semnificație statistică stabilit. În mod convențional, optimizatorii încearcă să atingă marca de încredere statistică de 95%, deoarece vă lasă o șansă de 5% să faceți eroarea de tip I care este considerată suficient de mică pentru majoritatea experimentelor de optimizare. În general, cu cât această măsurătoare este mai mare, cu atât sunt mai mici șansele de a face erori de tip I.

Nivelul de încredere pe care îl urmăriți determină care va fi probabilitatea de a obține o eroare de tip I (α).

Deci, dacă țintiți la un nivel de încredere de 95%, valoarea dvs. pentru α devine 5%. Aici, acceptați că există o șansă de 5% ca concluzia dvs. să fie greșită.

Spre deosebire de aceasta, dacă experimentați cu un nivel de încredere de 99%, probabilitatea de a obține o eroare de tip I scade la 1%.

Să spunem, pentru acest experiment, că devii prea nerăbdător și, în loc să aștepți să se încheie experimentul, te uiți la tabloul de bord al instrumentului tău de testare (peek!) doar la o zi. Și observați o creștere „aparentă” - că rata de completare a formularelor a crescut cu 29,2%, cu un nivel de încredere de 95%.

Și BAM...

… vă opriți experimentul.

… respinge ipoteza nulă (că insignele nu au avut impact asupra vânzărilor).

… acceptați ipoteza alternativă (că insignele au stimulat vânzările).

… și rulați cu versiunea cu insignele de premii.

Dar, pe măsură ce vă măsurați clienții potențiali de-a lungul lunii, găsiți că numărul este aproape comparabil cu ceea ce ați raportat cu versiunea originală. La urma urmei, insignele nu contau atât de mult. Și că ipoteza nulă a fost probabil respinsă în zadar.

Ceea ce s-a întâmplat aici a fost că ai încheiat experimentul prea devreme și ai respins ipoteza nulă și ai ajuns cu un câștigător fals - făcând o eroare de tip I.

Evitarea erorilor de tip I în experimentele dvs

O modalitate sigură de a vă reduce șansele de a lovi o eroare de tip I este să mergeți cu un nivel de încredere mai ridicat. Un nivel de semnificație statistică de 5% (care se traduce într-un nivel de încredere statistică de 95%) este acceptabil. Este un pariu pe care majoritatea optimizatorilor l-ar face în siguranță, deoarece, aici, veți eșua în intervalul puțin probabil de 5%.

Pe lângă stabilirea unui nivel ridicat de încredere, este important să rulați testele pentru o perioadă suficient de lungă. Calculatoarele de durată a testului vă pot spune pentru cât timp trebuie să rulați testul (după ce luați în considerare lucruri precum dimensiunea unui efect specificat, printre altele). Dacă lăsați un experiment să urmeze cursul dorit, vă reduceți semnificativ șansele de a întâmpina eroarea de tip 1 (având în vedere că utilizați un nivel de încredere ridicat). Așteptarea până când ajungeți la rezultate semnificative din punct de vedere statistic vă asigură că există doar o șansă mică (de obicei 5%) ca să respingeți ipoteza nulă în mod eronat și să comiteți o eroare de tip I. Cu alte cuvinte, utilizați o dimensiune bună a eșantionului, deoarece aceasta este esențială pentru a obține rezultate semnificative statistic.

Acum, asta era totul despre erorile de tip I care sunt legate de nivelul de încredere (sau de semnificație) în experimentele dvs. Dar există și un alt tip de eroare care se poate strecura în testele tale - erorile de tip II.

Înțelegerea erorilor de tip II

Erorile de tip II sunt cunoscute ca fals negative sau erori Beta.

Spre deosebire de eroarea de tip I, în cazul unei erori de tip II, experimentul *PARE A FIE NERECUCIT (SAU INCONCLUSIV)* și tu (în mod eronat) concluzionezi că variația pe care o testați nu face nimic diferit de original.

În erorile de tip II, nu reușești să vezi creșterile sau scăderile reale și ajungi să eșuezi să respingi ipoteza nulă și să respingi ipoteza alternativă.

Iată cum ați putea face eroarea de tip II:

Revenind la același site B2B de sus...

Așadar, să presupunem că de data aceasta emiteți ipoteza că adăugarea unei declinări de responsabilitate a conformității GDPR în partea de sus a formularului va încuraja mai mulți clienți potențiali să o completeze (rezultând mai mulți clienți potențiali).

Prin urmare, ipoteza dvs. nulă pentru acest experiment devine: declinarea răspunderii conform GDPR nu afectează completarea formularelor.

Iar ipoteza alternativă pentru aceeași este: declinarea răspunderii pentru conformitate GDPR are ca rezultat mai multe completări de formulare.

Puterea statistică a unui test determină cât de bine poate detecta diferențele de performanță a versiunilor originale și challenger, în cazul în care există abateri. În mod tradițional, optimizatorii încearcă să atingă marca de putere statistică de 80%, deoarece cu cât această măsurătoare este mai mare, cu atât sunt mai mici șansele de a face erori de tip II.

Puterea statistică ia o valoare între 0 și 1 (și este adesea exprimată în %) și controlează probabilitatea erorii dvs. de tip II (β); se calculează ca: 1 – β

Cu cât este mai mare puterea statistică a testului dumneavoastră, cu atât va fi mai mică probabilitatea de a întâlni erori de tip II.

Deci, dacă un experiment are o putere statistică de 10%, atunci poate fi destul de susceptibil la o eroare de tip II. În timp ce, dacă un experiment are o putere statistică de 80%, va fi mult mai puțin probabil să facă o eroare de tip II.

Din nou, executați testul, dar de data aceasta nu observați nicio creștere semnificativă în completarea formularelor. Ambele versiuni raportează aproape conversii similare. Din acest motiv, vă opriți experimentul și continuați cu versiunea originală fără declinarea răspunderii la GDPR.

Cu toate acestea, pe măsură ce cercetați mai adânc în datele dvs. de clienți potențiali din perioada experimentului, descoperiți că, deși numărul de clienți potențiali din ambele versiuni (original și contestator) părea identic, versiunea GDPR v-a adus o creștere bună și semnificativă a numărului. de piste din Europa. (Desigur, ați fi putut folosi direcționarea către public pentru a arăta experimentul doar clienților potențiali din Europa – dar asta este o altă poveste.)

Ceea ce s-a întâmplat aici a fost că ți-ai încheiat testul prea devreme, fără a verifica dacă ai atins suficientă putere - făcând o eroare de tip II.

Evitarea erorilor de tip II în experimentele dvs

Pentru a evita erorile de tip II, executați teste cu putere statistică mare. Încercați să configurați experimentele astfel încât să puteți atinge cel puțin marca de putere statistică de 80%. Acesta este un nivel acceptabil de putere statistică pentru majoritatea experimentelor de optimizare. Cu acesta, vă puteți asigura că, în cel puțin 80% din cazuri, veți respinge corect o ipoteză nulă falsă.

Pentru a face acest lucru, trebuie să vă uitați la factorii care se adaugă.

Cea mai mare dintre acestea este dimensiunea eșantionului (dată fiind dimensiunea efectului observat). Mărimea eșantionului se leagă direct de puterea unui test. O dimensiune mare a eșantionului înseamnă un test de mare putere. Testele cu putere redusă sunt foarte vulnerabile la erorile de tip II, deoarece șansele dvs. de a detecta diferențe între rezultatele challenger-ului și versiunile originale se reduc foarte mult, în special pentru MEI scăzute (mai multe despre asta mai jos). Deci, pentru a evita erorile de tip II, așteptați ca testul să acumuleze suficientă putere pentru a minimiza erorile de tip II. În mod ideal, pentru majoritatea cazurilor, ați dori să ajungeți la o putere de cel puțin 80%.

Un alt factor este efectul minim de interes (MEI) pe care îl vizați pentru experiment. MEI (numit și MDE) este magnitudinea minimă a diferenței pe care ați dori să o detectați în KPI-ul în cauză. Dacă setați un MEI scăzut (observând o creștere de 1,5%, de exemplu), șansele dvs. de a întâlni eroarea de tip II cresc, deoarece detectarea diferențelor mici necesită dimensiuni substanțial mai mari ale eșantionului (pentru a obține o putere suficientă).

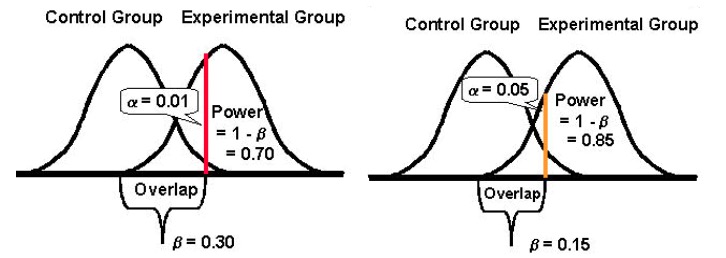
Și, în sfârșit, este important de menționat că tinde să existe o relație inversă între probabilitatea de a face o eroare de tip I (α) și probabilitatea de a face o eroare de tip II (β). De exemplu, dacă reduceți valoarea lui α pentru a reduce probabilitatea de a face o eroare de tip I (să ​​spunem că ați stabilit α la 1%, adică un nivel de încredere de 99%), puterea statistică a experimentului dvs. (sau capacitatea sa, β , de a detecta o diferență atunci când aceasta există) ajunge să se reducă și, crescând astfel probabilitatea de a obține o eroare de tip II.

Acceptarea mai mare a oricăreia dintre erori: Tipul I și II (și atingerea unui echilibru)

Scăderea probabilității unui tip de eroare o crește pe cea a celuilalt tip (având în vedere că toate celelalte rămân aceleași).

Și deci trebuie să răspundeți la ce tip de eroare ați putea fi mai tolerant.

Efectuarea unei erori de tip I, pe de o parte, și lansarea unei modificări pentru toți utilizatorii dvs. ar putea costa conversii și venituri - și mai rău, ar putea fi și un ucigaș de conversie.

Pe de altă parte, a face o eroare de tip II și a nu lansa o versiune câștigătoare pentru toți utilizatorii dvs. ar putea, din nou, să vă coste conversiile pe care le-ați fi câștigat altfel.

Invariabil, ambele erori au un cost.

Cu toate acestea, în funcție de experimentul dvs., unul ar putea fi mai acceptabil pentru dvs. decât celălalt. În general, testerii găsesc eroarea de tip I de aproximativ patru ori mai gravă decât eroarea de tip II .

Dacă doriți să adoptați o abordare mai echilibrată, statisticianul Jacob Cohen sugerează că ar trebui să alegeți o putere statistică de 80% care vine cu „ un echilibru rezonabil între riscul alfa și beta. ” (80% putere este, de asemenea, standardul pentru majoritatea instrumentelor de testare.)

Și în ceea ce privește semnificația statistică, standardul este stabilit la 95%.

Practic, totul este despre compromis și nivelul de risc pe care ești dispus să-l tolerezi. Dacă doriți să minimizați cu adevărat șansele ambelor erori, ați putea alege un nivel de încredere de 99% și o putere de 99%. Dar asta ar însemna că ai lucra cu eșantioane de dimensiuni imposibil de uriașe pentru perioade care par etern lungi. În plus, chiar și atunci ai lăsa un loc pentru erori.

Din când în când, veți încheia un experiment greșit. Dar asta face parte din procesul de testare - durează ceva timp pentru a stăpâni statisticile de testare A/B. Investigarea și retestarea sau urmărirea experimentelor dvs. de succes sau eșuate este o modalitate de a vă reafirma constatările sau de a descoperi că ați făcut o greșeală.