Rețea neuronală cu un singur neuron pe Python - Cu intuiție matematică

Să construim o rețea simplă – foarte, foarte simplă, dar o rețea completă – cu un singur strat. O singură intrare - și un neuron (care este și ieșirea), o greutate, o părtinire.

Să rulăm mai întâi codul și apoi să analizăm parte cu parte

Clonează proiectul Github sau pur și simplu rulează următorul cod în IDE-ul tău preferat.

Dacă aveți nevoie de ajutor la configurarea unui IDE, am descris procesul aici.

Dacă totul merge bine, veți obține această ieșire:

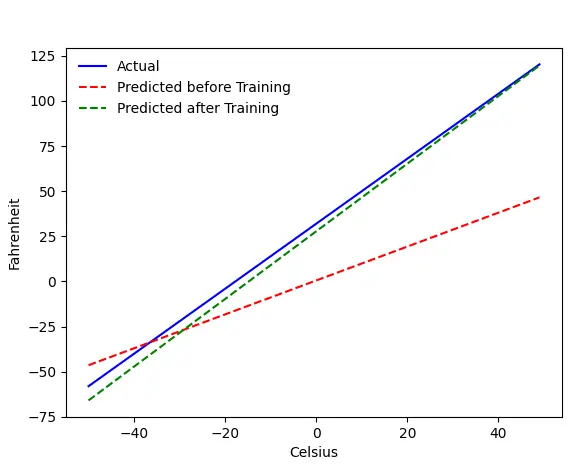
Problema - Fahrenheit de la Celsius

Ne vom antrena mașina să prezică Fahrenheit de la Celsius. După cum puteți înțelege din cod (sau grafic), linia albastră este relația reală Celsius-Fahrenheit. Linia roșie este relația prezisă de aparatul nostru pentru bebeluși fără niciun antrenament. În cele din urmă, antrenăm mașina, iar linia verde este predicția după antrenament.

Uită-te la rândul #65–67 — înainte și după antrenament, se prezice folosind aceeași funcție ( get_predicted_fahrenheit_values() ). Deci ce tren magic() face? Să aflăm.

Structura rețelei

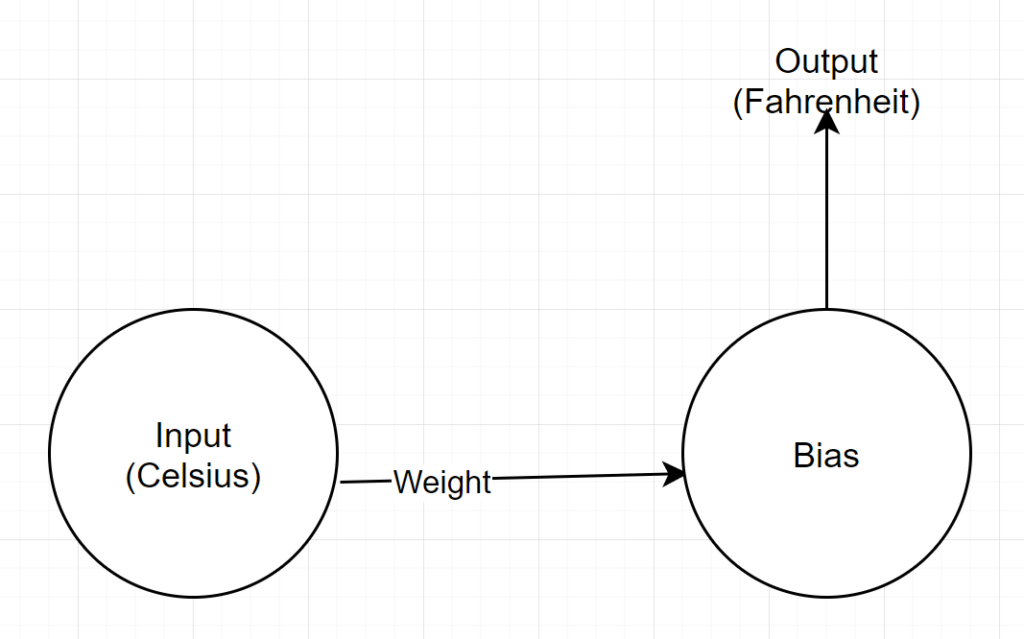
Intrare: un număr care reprezintă celsius

Greutate: un plutitor care reprezintă greutatea

Bias: un float care reprezintă părtinire

Ieșire: un float reprezentând Fahrenheit estimat

Deci, avem în total 2 parametri - 1 greutate și 1 părtinire

Analiza codului

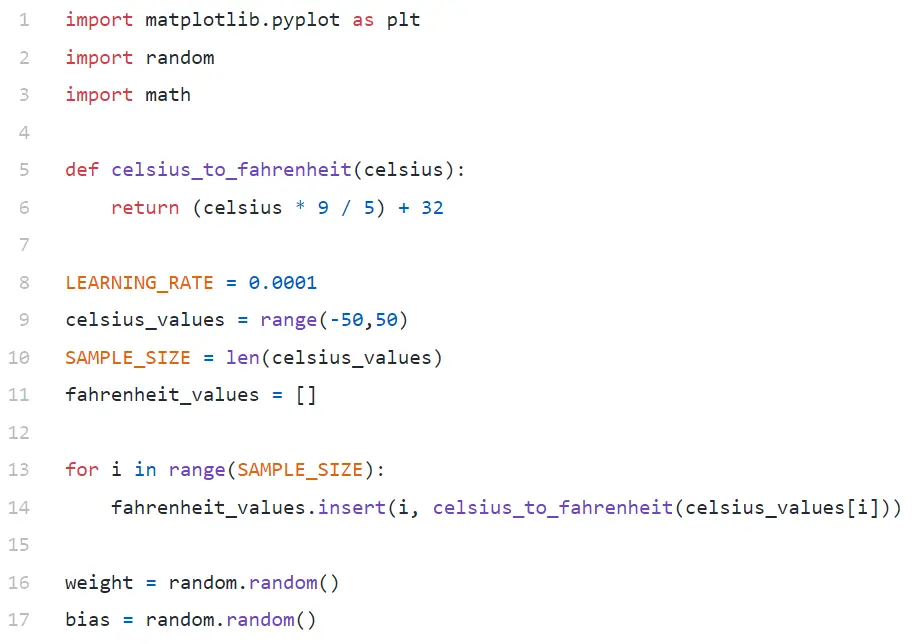
În linia #9, generăm o matrice de 100 de numere între -50 și +50 (excluzând 50 - funcția de interval exclude valoarea limită superioară).

În rândul #11–14, generăm Fahrenheit pentru fiecare valoare celsius.

În rândurile #16 și #17, inițializam greutatea și părtinirea.

tren()

Derulăm 10.000 de iterații de instruire aici. Fiecare iterație este alcătuită din:

1. înainte (linia #57) trece
2. trece înapoi (linia#58).
3. update_parameters (linia#59)

Dacă sunteți nou în python, s-ar putea să vă pară puțin ciudat - funcțiile python pot returna mai multe valori ca tuple .

Observați că update_parameters este singurul lucru care ne interesează. Tot ceea ce facem aici este să evaluăm parametrii acestei funcții, care sunt gradienții (vom explica mai jos ce sunt gradienții) ponderii și părtinirii noastre.

1. grad_weight: un float reprezentând gradient de greutate
2. grad_bias: Un float reprezentând gradient de părtinire

Obținem aceste valori apelând înapoi, dar necesită ieșire, pe care o obținem apelând înainte la rândul #57.

redirecţiona()

Observați că aici celsius_values ​​și fahrenheit_values ​​sunt matrice de 100 de rânduri:

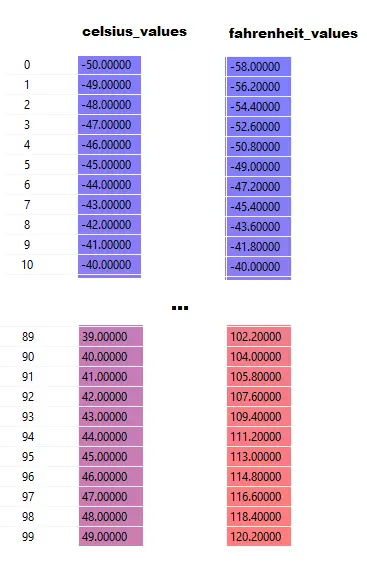
După executarea liniei #20–23, pentru o valoare celsius, să spunem 42

ieșire = 42 * greutate + părtinire

Deci, pentru 100 de elemente în celsius_values ​​, ieșirea va fi o matrice de 100 de elemente pentru fiecare valoare celsius corespunzătoare.

Linia #25–30 calculează pierderea utilizând funcția de pierdere Eroare pătratică medie (MSE), care este doar un nume de lux al pătratului tuturor diferențelor împărțit la numărul de mostre (100 în acest caz).

Pierderea mică înseamnă o predicție mai bună. Dacă continuați pierderea prin imprimare la fiecare iterație, veți vedea că aceasta scade pe măsură ce antrenamentul progresează.

În cele din urmă, în rândul #31, returnăm rezultatul și pierderile estimate.

înapoi

Suntem interesați doar să ne actualizăm greutatea și părtinirea. Pentru a actualiza aceste valori, trebuie să le cunoaștem gradienții și asta este ceea ce calculăm aici.

Observați că gradienții sunt calculati în ordine inversă. Gradientul de ieșire este calculat mai întâi, apoi pentru greutate și părtinire, deci numele „backpropagation”. Motivul este, pentru a calcula gradientul greutății și părtinirea, trebuie să cunoaștem gradientul de ieșire - astfel încât să îl putem folosi în formula regulii lanțului .

Acum să aruncăm o privire la ce sunt regulile gradientului și ale lanțului.

Gradient

De dragul simplității, considerăm că avem o singură valoare a valorilor_celsius și valorilor_fahrenheit , 42 și respectiv 107,6 .

Acum, defalcarea calculului din rândul #30 devine:

pierdere = (107,6 — (42 * greutate + părtinire))² / 1

După cum vedeți, pierderea depinde de 2 parametri - greutăți și părtinire. Luați în considerare greutatea. Imaginați-vă că am inițializat-o cu o valoare aleatorie, să zicem, 0,8, iar după evaluarea ecuației de mai sus, obținem 123,45 ca valoare a pierderii . Pe baza acestei valori de pierdere, trebuie să decideți cum veți actualiza greutatea. Ar trebui să-l faci 0,9 sau 0,7?

Trebuie să actualizați greutatea într-un mod astfel încât în ​​următoarea iterație să obțineți o valoare mai mică pentru pierdere (rețineți că reducerea la minimum a pierderii este scopul final). Deci, dacă creșterea în greutate crește pierderea, o vom scădea. Și dacă creșterea în greutate scade pierderea, o vom crește.

Acum, întrebarea, cum știm dacă creșterea greutății va crește sau scade pierderea. Aici intervine gradientul . În linii mari, gradientul este definit prin derivată. Amintiți-vă, din calculul de liceu, ∂y/∂x (care este derivată parțială/gradient a lui y față de x) indică modul în care y se va schimba cu o mică modificare a lui x.

Dacă ∂y/∂x este pozitivă, înseamnă că un mic increment în x va crește y.

Dacă ∂y/∂x este negativ, înseamnă că un mic increment în x va scădea y.

Dacă ∂y/∂x este mare, o mică modificare în x va determina o schimbare mare în y.

Dacă ∂y/∂x este mic, o mică modificare în x va determina o mică modificare în y.

Deci, din gradienți, obținem 2 informații. În ce direcție trebuie actualizat parametrul (creștere sau descreștere) și cât de mult (mare sau mic).

Regula lanțului

Informal vorbind, regula lanțului spune:

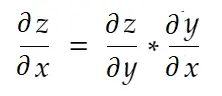
Luați în considerare exemplul de greutate de mai sus. Trebuie să calculăm grad_weight pentru a actualiza această greutate, care va fi calculată prin:

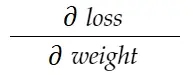
Cu formula de regulă a lanțului, o putem deriva:

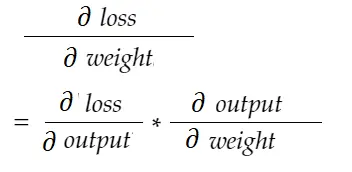
În mod similar, gradient pentru părtinire:

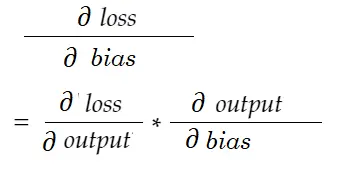
Să desenăm o diagramă de dependență.

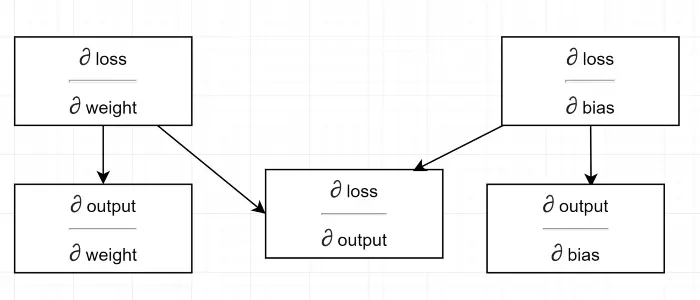
A se vedea tot calculul depinde de gradientul de ieșire (∂ pierdere/∂ ieșire) . De aceea îl calculăm mai întâi pe trecerea înapoi (linia #34–36).

De fapt, în cadrele ML de nivel înalt, de exemplu în PyTorch, nu trebuie să scrieți coduri pentru backpass! În timpul trecerii înainte, creează grafice de calcul, iar în timpul trecerii înapoi, trece prin direcția opusă în grafic și calculează gradienții folosind regula lanțului.

∂ pierdere / ∂ ieșire

Definim această variabilă prin grad_output în cod, pe care l-am calculat în rândul #34–36. Să aflăm motivul din spatele formulei pe care am folosit-o în cod.

Amintiți-vă, alimentăm împreună toate cele 100 de valori celsius din mașină. Deci, grad_output va fi o matrice de 100 de elemente, fiecare element conținând gradient de ieșire pentru elementul corespunzător în celsius_values ​​. Pentru simplitate, să luăm în considerare că există doar 2 elemente în celsius_values ​​.

Deci, defalcând linia # 30,

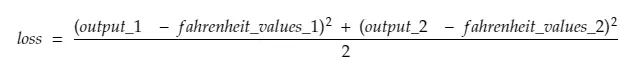
Unde,

output_1 = valoarea de ieșire pentru prima valoare celsius

output_2 = valoarea de ieșire pentru a 2-a valoare celsius

fahreinheit_values_1 = Valoarea reală fahreinheit pentru prima valoare celsius

fahreinheit_values_1 = Valoarea reală Fahreinheit pentru valoarea a 2-a celsius

Acum, variabila rezultată grad_output va conține 2 valori — gradientul output_1 și output_2, adică:

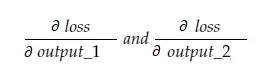
Să calculăm doar gradientul output_1 și apoi putem aplica aceeași regulă pentru celelalte.

Timp de calcul!

Care este același cu rândul #34–36.

Gradient de greutate

Imaginați-vă că avem un singur element în celsius_values. Acum:

Care este la fel ca și linia #38–40. Pentru 100 celsius_values, valorile gradientului pentru fiecare dintre valori vor fi însumate. O întrebare evidentă ar fi de ce nu reducem rezultatul (adică împărțim cu SAMPLE_SIZE). Deoarece înmulțim toți gradienții cu un factor mic înainte de a actualiza parametrii, nu este necesar (vezi ultima secțiune Actualizarea parametrilor).

Gradient de părtinire

Care este la fel cu Linia #42. La fel ca gradienții de greutate, aceste valori pentru fiecare dintre cele 100 de intrări sunt însumate. Din nou, este bine, deoarece gradienții sunt înmulțiți cu un factor mic înainte de a actualiza parametrii.

Actualizarea parametrilor

În cele din urmă, actualizăm parametrii. Observați că gradienții s-au înmulțit cu un factor mic (LEARNING_RATE) înainte de a fi scăzuți, pentru a face antrenamentul stabil. O valoare mare a LEARNING_RATE va cauza o problemă de depășire , iar o valoare extrem de mică va face antrenamentul mai lent, ceea ce ar putea necesita mai multe iterații. Ar trebui să găsim o valoare optimă pentru el cu unele încercări și erori. Există multe resurse online, inclusiv aceasta pentru a afla mai multe despre rata de învățare.

Observați că, suma exactă pe care o ajustăm nu este extrem de critică. De exemplu, dacă reglați puțin LEARNING_RATE, variabilele descent_grad_weight și descent_grad_bias (linia #49–50) vor fi modificate, dar mașina ar putea funcționa în continuare. Lucrul important este să vă asigurați că aceste sume sunt derivate prin reducerea gradienților cu același factor (LEARNING_RATE în acest caz). Cu alte cuvinte, „păstrarea proporțională a coborârii gradienților” contează mai mult decât „cât de mult coboară ”.

De asemenea, observați că aceste valori ale gradientului sunt de fapt o sumă a gradienților evaluați pentru fiecare dintre cele 100 de intrări. Dar, deoarece acestea sunt scalate cu aceeași valoare, este bine așa cum am menționat mai sus.

Pentru a actualiza parametrii, trebuie să îi declarăm cu cuvântul cheie global (în rândul #47).

Unde să mergi de aici

Codul ar fi mult mai mic prin înlocuirea buclelor for cu înțelegerea listei în mod pythonic. Aruncă o privire acum - nu ar dura mai mult de câteva minute pentru a înțelege.

Dacă ați înțeles totul până acum, probabil că este un moment bun pentru a vedea elementele interne ale unei rețele simple cu neuroni/straturi multiple - iată un articol.