Distribuție normală – o introducere intuitivă fără matematică

Voi încerca să mențin acest articol fără ecuații și jargon gura — cât mai mult posibil. Totuși, am nevoie să aveți cel puțin următoarele capacități:

• Capabil să interpreteze grafice simple.
• Cunoștințe de nivel elementar în probabilitate. Înțelegi cel puțin că există o probabilitate de 50% pentru cap dacă arunc o monedă.
• Calcul integral și fizica cuantică (glumesc!)

De ce distribuție normală

O modalitate intuitivă de a înțelege ceva este să investighezi de ce este nevoie. Să o facem pentru distribuția normală (numită și Distribuție Gaussiană).

Spuneți că aveți un obicei amuzant. În fiecare zi arunci o monedă de 100 de ori. Este „normal” să te aștepți că vei avea cap de 50 de ori – sau aproape de 50 de ori în cea mai mare parte a zilei. Rareori, există zile bune pentru cap - s-ar putea să ajungi de aproximativ 55 de ori și foarte rar de peste 65 de ori.

Acum, doriți să cuantificați această „raritate”. Deci, începi să ții evidența de câte ori ai primit capul în fiecare zi.

Numărul de capete în fiecare zi într-un an

Mai jos sunt datele după un an (365 de zile) — primul este numărul de capete pe care le-ați primit în prima zi, iar ultimul este numărul de capete pe care le-ați primit în ultima zi. Nu trebuie să verificați toate numerele de mai jos, dar este ușor de observat că majoritatea sunt în jur de 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 48, 6 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 4 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 4 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 4 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 4 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 53, 53, 53 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 4 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 43, 46 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 53, 5, 5 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 57, 57 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 44, 44 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 5 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 4. 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 4 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Vizualizați mai bine cu histogramă

Să trasăm o histogramă din datele de mai sus:

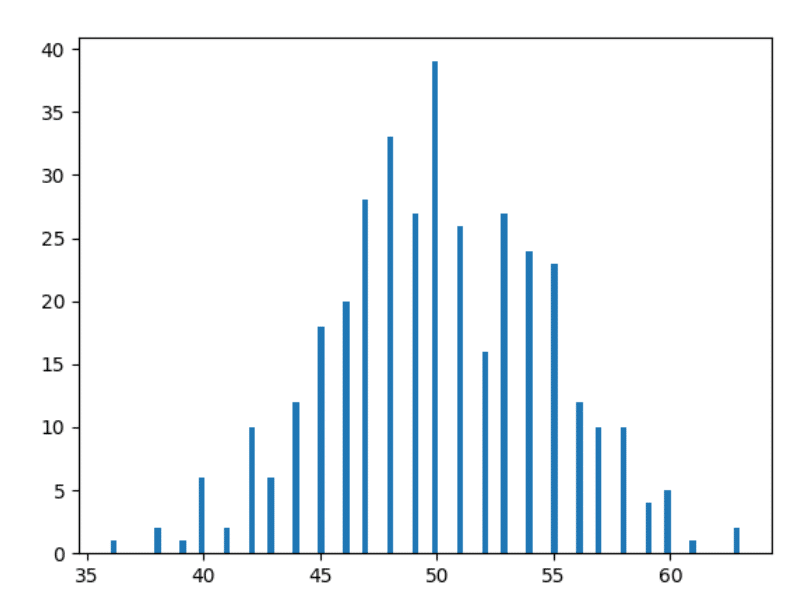
Aha! Nu seamănă deja cu imaginea pe care ai văzut-o pe internet când ai căutat pe google „Distribuție normală”? Aproape am ajuns!

Deci, dacă nu înțelegeți histogramele - tocmai am reprezentat aici numărul de zile în care am primit un anumit număr pentru cap. De exemplu, am primit capul de 36 de ori în 2 anumite zile ale anului (verificați datele de mai sus dacă nu mă credeți), de aceea există o bară de înălțime de 2 unități pe punctul orizontal la 36 (roșu dreptunghi din stânga în imaginea de mai jos).

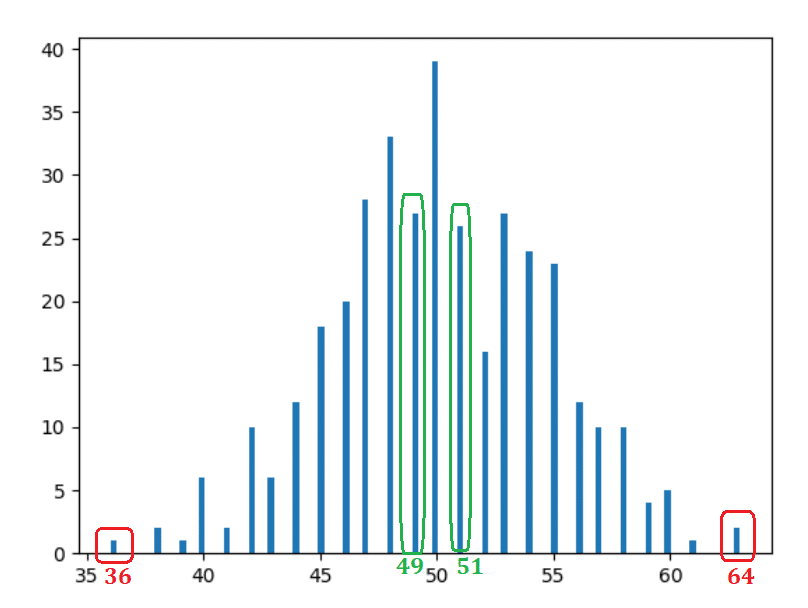
Observatii

1. Destul de evident și de așteptat - 50 de capete au apărut de cele mai multe ori.
2. Cu cât ne depărtăm de centru (50), apariția este în cea mai mare parte în scădere.
3. Barele aflate la aceeași distanță iau forme similare. De exemplu, dacă mutați o unitate la stânga (49) sau la dreapta (51) — aparițiile sunt similare — 30 și, respectiv, 31 (dreptunghiurile verzi). Dacă mutați 14 unități la stânga (36) sau la dreapta (64), aparițiile sunt din nou similare - 2 și, respectiv, 1 (dreptunghiuri roșii).

Date de 10 ani

Acum haideți să avansăm puțin – și să reprezentăm datele de 10 ani.

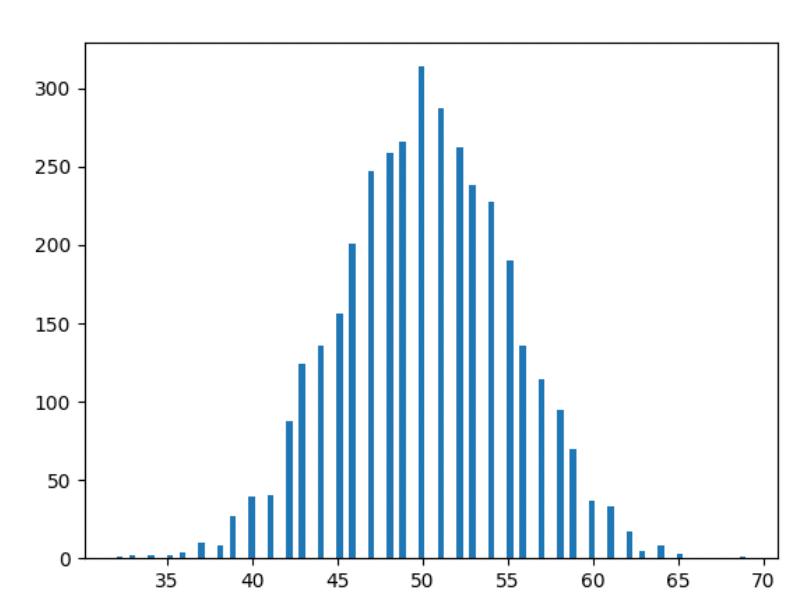
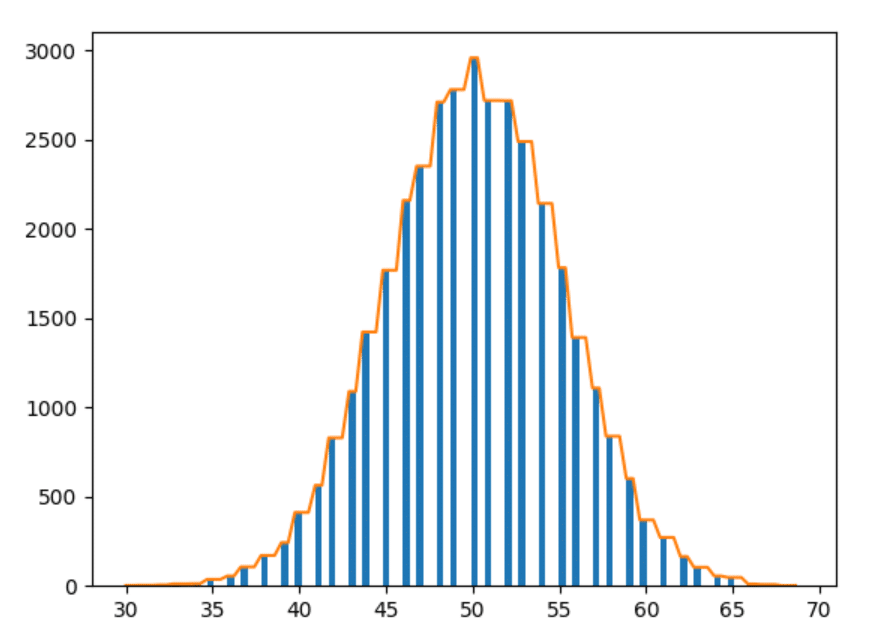
Date de 1000 de ani

Bine - ultimul. Să reprezentăm datele a 1000 de ani.

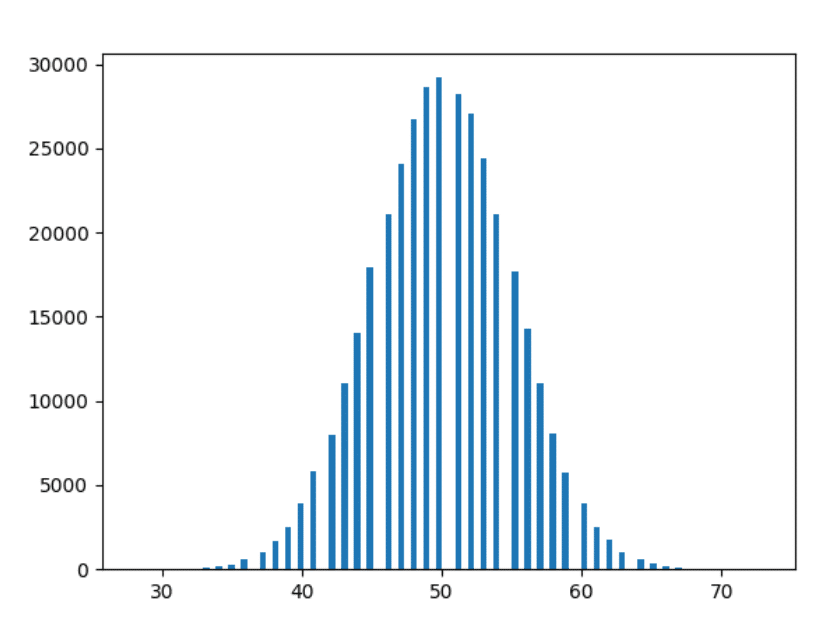
Observatii

1. Cu cât experimentăm mai mult, cu atât formele sunt mai fine.
2. Cu cât experimentăm mai mult, cu atât barele urmăresc observațiile de mai sus (adică barele aflate la o distanță similară iau forme mai apropiate).

Unde este al naibii de distribuție normală

Bine — prea mult fundal — acum să trecem la subiect.

Să vedem răspunsul sugerat de Google:

Câteva lucruri în această definiție:

Variabilă aleatorie: Mai simplu spus - o variabilă aleatorie este un set de valori posibile ale unui experiment aleatoriu, cum ar fi aruncarea unei monede. În exemplul nostru, valoarea posibilă a experimentului nostru este Cap sau coadă .

În formă de clopot: Ați observat că histograma noastră ia formă de clopot?

Simetric: barele aflate la aceeași distanță au forme similare - nu este simetric?

Deci, distribuția normală reprezintă distribuția rezultatelor pentru evenimente precum aruncarea monedelor - unde distribuția tinde să mențină câteva proprietăți, inclusiv simetria și forma clopotului.

Ce fenomene în afară de aruncarea monedelor urmează distribuția normală?

Câteva exemple interesante aici.

• Înălțimea populației – mai mulți oameni se încadrează în grupul de înălțime medie. Este rar să găsești oameni extrem de înalți sau extrem de scunzi. Și șansele de a găsi extrem de înalt și extrem de scund sunt aproape egale.
• Rularea unui zar
• Mărimea pantofului
• IQ
• Si multe altele…

Urmează aceste fenomene cu strictețe distribuția normală?

Răspunsul simplu este nu. Deși, așa cum am văzut mai sus, cu cât experimentezi mai mult, cu atât datele vor urma proprietățile normale de distribuție. Dar nu există nicio asigurare că un eveniment improbabil nu va avea loc oricum.

Sunt toate distribuțiile de probabilitate din univers distribuție normală?

Nu. Există multe fenomene care sunt determinate de un alt tip de distribuție.

• Probabilitatea ca un anumit număr de clienți să sosească, apelurile telefonice, accidentele, evenimentele sportive și inundațiile urmează distribuția Poisson .
• Pentru vânzările de afaceri, 20% dintre clienții unei companii sunt responsabili pentru 80% din vânzări. ( Distribuția Pareto )
• Tipare de trafic într-un oraș — Distribuție exponențială
• Selectarea aleatorie a membrilor unei echipe dintr-o populație de fete și băieți — Distribuție hipergeometrică

Si multe altele …

Am produs lista de mai sus doar căutând pe google „exemple din viața reală” cu unele distribuții enumerate aici - nu că le înțeleg pe toate. 😉

Există vreun motiv pentru care unele fenomene naturale tind să urmeze distribuția normală

Da, citând explicația mea preferată:

Explicația obișnuită este dată de un alt nume pentru distribuția normală, care este „distribuția de eroare”. Ideea este că erorile sunt în general aleatorii, astfel încât sunt la fel de probabil să meargă într-o direcție ca și în cealaltă. De exemplu, trăgătorul este la fel de probabil să tragă puțin la stânga, la fel de puțin spre dreapta sau puțin sus, cât și puțin jos. Astfel, un grafic cu cât de departe sunt fotografiile de ochiul va reflecta această tendință aleatorie și va fi simetric în jurul valorii medii. În mod similar, cu înălțimea și inteligența - multe gene (poate mii) contribuie la aceste rezultate, la fel ca un număr mare de factori de mediu, cum ar fi nutriția, bolile, veniturile scăzute și așa mai departe.

Parametrii distribuției normale

Dacă ai avut o intuiție a discuției până acum — ești deja câștigătorul. Misiune indeplinita. Restul articolului este un bonus.

Toate graficele de distribuție normale pe care le vedeți sunt diferite ca formă. Unele dintre ele sunt mai plate decât altele. Unii dintre ei au înălțimi bune. Toate aceste forme sunt controlate de doar 2 parametri:

Rău

Media este definită de medie. Acesta definește înălțimea clopotului. Pentru exemplul de aruncare a monedelor, media este aproape de 50, care este locația de sus a graficului.

Deviație standard

Deoarece promit că acest articol va fi lipsit de ecuații, nu vă ofer aici reprezentarea sa matematică. Dar oricum nu este atât de greu. Abaterea standard este o măsură pentru a reprezenta cât de variate sunt datele.

De exemplu, abaterea standard a vârstei în îngrijirea copiilor va fi mai mică decât abaterea standard a vârstei în clubul de fani ai fotbalului, deoarece diferența de vârstă dintre grupul cel mai tânăr și cel mai în vârstă ar trebui să fie mult mai mare în clubul de fani ai fotbalului.

Abaterea standard determină lățimea curbei. O abatere standard mică produce o curbă abruptă, iar o abatere standard mai mare produce o curbă mai plată.