Simțiți calculul cu simțul dvs. de programare

Cred că oamenii care pot codifica — au capacitatea de a înțelege concepte mai complicate decât calculul. Unul dintre motivele pentru care există mulți programatori talentați care încă se luptă cu calculul nu este că este greu. Mai ales pentru că am fost învățați în mod greșit (împreună cu multe alte subiecte).

Dacă ai făcut ceva codificare în viața ta - chiar și unele exerciții de jucărie, cum ar fi generarea de numere prime, s-ar putea să fi făcut deja lucruri similare care se întâmplă în calcul, dar nu ai avut niciodată șansa de a relaționa.

Obiectivul acestei scrieri nu este nici să vă învețe calculul sau programarea, ci să vă ajute să conectați câteva puncte.

Voi ajunge la partea de codificare într-un minut. Dar permiteți-mi să vă ofer un scurt context înainte de asta.

Rata de schimbare

Calculul diferențial vorbește despre „rata schimbării”. Să încercăm să înțelegem ce înseamnă asta.

Pentru o modificare a unei variabile (x), rata de modificare a unei funcții este pur și simplu modificarea funcției împărțită la modificarea lui x. Să vizualizăm cu numere reale:

Se consideră 2 puncte x=2 și x=6 și o funcție y=f(x) = x².

De asemenea, luați în considerare dx = distanța dintre aceste 2 puncte din axa x. Și dy este distanța dintre valorile y pentru aceste valori x.

Atunci, rata de schimbare a lui y de la x=2 la x=6 este

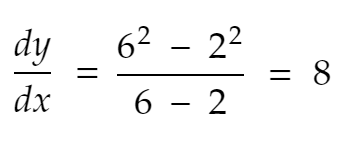
Derivat

Acum — derivata dy/dx este rata de schimbare a lui y pentru o modificare infinitezimal mică a lui x. Deoarece această distanță (6–2=4) nu este infinitezimal de mică - nici măcar aproape, nu putem numi ecuația de mai sus o derivată. Deci, să alegem un număr mai mic, 0,1, pentru moment.

Când x = 0, y = x² = 0² = 0.

Cel mai apropiat vecin de direcția pozitivă, x = 0,1. Acolo y devine 0,1² = 0,01.

Asa de,

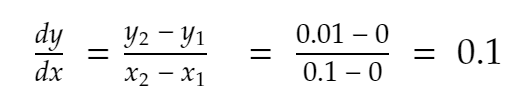
Să mai încercăm o dată. Cel mai apropiat vecin de 0,1 de direcția pozitivă, x = 0,2. Deci, y devine 0,2² = 0,04. Asa de,

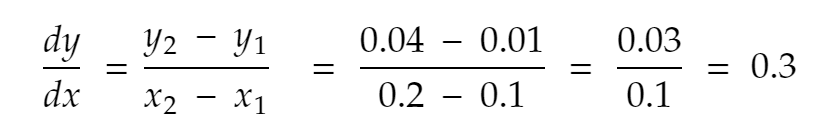
Dacă repetăm ​​procesul de câteva ori, iată ce obținem:

Aici este fișierul excel dacă doriți să jucați cu el.

dx (care este distanța noastră infinitezimal fictivă dintre 2 puncte adiacente de pe axa x) este 0,1 în contextul nostru.

x crește în consecință.

y este pur și simplu x².

dy este distanța dintre 2 valori y adiacente. De exemplu, când x= 0,1, distanța dintre curentul y (0,01 ) și următorul y (0,04) este 0,03 - deci, dy este 0,03 la x=0,1.

dy/dx este dy împărțit la dx.

dy/dx / x este dy/dx împărțit la x.

Acum observați că, pe măsură ce x crește, ultimul rând se apropie de 2, ceea ce înseamnă că — rata de schimbare a lui x² față de x se apropie de două ori de x, care este 2x .

Vă amintiți derivata lui x² față de x? 2x! Găsiți o legătură?

Timp de codare

Să încercăm lucrurile din cod despre care am discutat până acum.

Presupunând că aveți deja instalat Python, în terminal, rulați:

După aceea, rulați următorul cod Python:

Aici:

x : care conține numere de la 0 la 9.

y : o altă matrice, fiecare element este pătrat al elementului x corespunzător

dy : O altă matrice inițializată cu zerouri. Vom pune distanțe y în această matrice.

dydx : O altă matrice inițializată cu zerouri. Acesta va conține valoarea dy/dx a fiecărui punct.

dx : Destul de evident - este dimensiunea pasului. Distanța dintre 2 numere consecutive, care scade pe măsură ce crește SIZE. Dacă SIZE = 10, dx = 1. Dacă SIZE = 100, dx = 0,1.

În primul rând, derivăm dy pentru fiecare punct. Apoi calculăm dydx din el.

Observa asta:

Aici omitem prima și ultima valoare. Prima valoare a lui x este 0, ceea ce va produce o eroare de diviziune zero. Și nu putem calcula ultima valoare a lui dy/dx, deoarece nu avem ultima valoare a lui dy - pentru că ar necesita lângă ultima valoare disponibilă a lui y, pe care nu o avem aici.

Dacă totul merge bine, veți obține acest grafic:

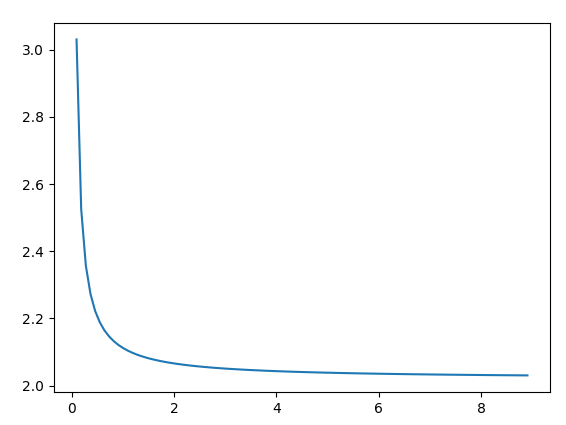
Ceea ce intelegi din intriga

După cum vedeți, graficul se apropie de 2. Creșteți valoarea SIZE (adică setarea mai mică a dx) și vedeți cum graficul se apropie mai repede de 2.

A doua derivată

Acum că ați ajuns până aici, mai sunt doar câțiva pași pentru a realiza derivata a doua, care vă va oferi intuiția pentru derivată de orice ordin.

După cum vă amintiți, a doua derivată este rata de modificare a primei derivate în raport cu x. Pur și simplu, dy/dx în derivata a doua este ca y în derivata întâi.

Să facem următoarele modificări codului de mai sus:

Declarați încă 2 matrice:

d2ydx2 : care va reprezenta derivata a doua:

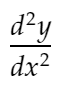
distance_dydx: Pentru a reprezenta distanța dintre valoarea dy/dx între 2 puncte adiacente

Iată codul complet pentru derivata a doua:

După calcularea dydx în bucla for, executăm o altă buclă pentru a calcula derivata a doua. Cu o codificare înțeleaptă, am putea calcula derivata a doua în aceeași buclă (încercați ca exercițiu) - dar le-am păstrat separate aici pentru claritate.

De asemenea, observați că:

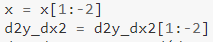
Așa cum am făcut în prima derivată, omitem și aici unele valori. Ultimele 2 valori sunt omise, deoarece a doua din ultima ar necesita ultima valoare „prima derivată”, pe care nu am putut-o calcula (din moment ce nu aveam valoarea y necesară pentru aceasta - așa cum este descris mai sus). Înseamnă că trebuie să omitem ultimele 3 valori în cazul derivatei a 3-a?🤔 — asta trebuie să găsiți.

Iată graficul de ieșire:

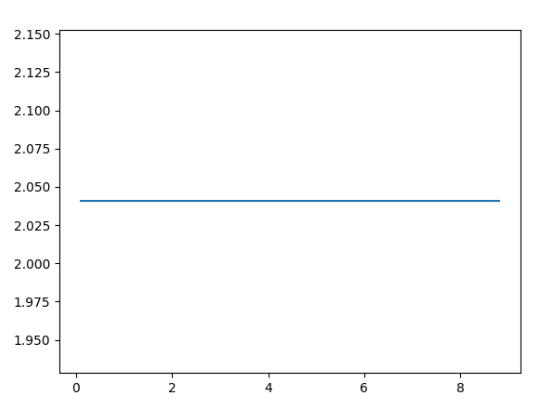
Ce vedem aici?

După cum știți din liceu:

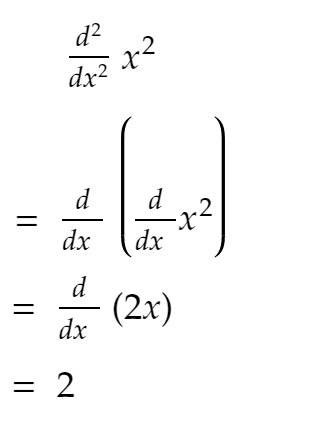
Acum, după cum vedeți din codul de mai sus, derivata a doua rămâne în mare parte constantă, iar dacă continuați să creșteți SIZE - se apropie de 2!

De ce este importantă rata de schimbare

S-ar putea să vă întrebați:

— De ce trecem prin toate aceste necazuri urâte? Ce informații utile obținem din rata de schimbare sau derivată?

— De ce nu putem merge cu rata de schimbare pentru orice sumă? De ce doar infinitezimal de mic? Ce informații obținem din rata de schimbare în raport cu infinitezimal mic , care nu poate fi găsită din rata de schimbare față de valori mai mari?

— Acest lucru infinitezimal de mic arată ca un hack? Am lucrat cu câteva numere mici mai sus, în regulă, dar cu siguranță nu de fapt infinitezimal de mici.

Dacă îmi permit să continui, ai pleca văzând lungimea acestui articol și nu ai fi ajuns atât de departe. Poate că vom aborda aceste întrebări într-o altă zi 😀.