Statistici bayesiene: un primer tester A/B rapid și fără hype
Publicat: 2022-06-23
Cât de încrezător sunteți în capacitatea dvs. de a interpreta rezultatele furnizate de instrumentul dvs. de testare A/B?
Să zicem că folosești un instrument construit pe statistici bayesiene și ți-a spus că „B” are șanse de 70% să învingă „A”, așa că „B” este câștigătorul. Știți ce înseamnă asta și cum ar trebui să vă informeze strategia CRO?
În acest articol, veți afla elementele fundamentale ale statisticilor bayesiene care vă vor ajuta să reveniți la controlul testării dvs. A/B, inclusiv
- O viziune imparțială asupra statisticilor bayesiene
- Avantaje și dezavantaje Frequentist vs Bayesian
- Pregătirea de care aveți nevoie pentru a interpreta și utiliza cu încredere rezultatele testelor Bayesian A/B, evitând în același timp unele capcane mituri comune.
- Ce este statistica bayesiană?
- Povestea originii bayesiene
- Un exemplu de statistică bayesiană aplicată testării A/B
- Un scurt glosar al termenilor bayesieni care contează pentru testerii A/B
- Inferența Bayesiană
- Probabilitate condițională
- Distribuția probabilității/Distribuția probabilității
- Distribuția anterioară a credinței
- Conjugarea
- Conjugați Priori
- Funcția de pierdere
- Ce este statistica frecventistă?
- Testare Bayesian vs Frequentist A/B
- Cadrul frecventist
- Cadrul Bayesian
- Ce vă spun de fapt statisticile bayesiene în testarea A/B?
- Probabilitatea de a fi cel mai bun (P2BB)
- Creștere așteptată
- Pierderea așteptată
- Mituri în jurul statisticilor bayesiene de evitat
- Mitul #1: Bayesienii își exprimă ipotezele, frecvențiștii nu
- Mitul #2. Metodele bayesiene vă oferă răspunsurile pe care le doriți de fapt
- Mitul #3: Inferența bayesiană vă ajută să comunicați incertitudinea mai bine decât inferența frecventistă
- Mitul #4. Rezultatele testării Bayesian A/B sunt imune la peeking
- Mitul #5. Statisticile Frecventist sunt ineficiente, deoarece trebuie să așteptați o dimensiune fixă a eșantionului
- Deci, ar trebui să alegeți Bayesian sau Frequentist? Există un loc pentru amândoi.
- Cheie la pachet
Gata? Să începem cu elementele de bază.
Ce este statistica bayesiană?
Statistica bayesiană este o abordare a analizei statistice care se bazează pe teorema lui Bayes, care actualizează convingerile despre evenimente pe măsură ce sunt colectate noi date sau dovezi despre acele evenimente. Aici, probabilitatea este o măsură a credinței că are loc un eveniment.
Ce înseamnă asta: dacă aveți o credință anterioară despre un eveniment și obțineți mai multe informații legate de acesta, acea credință se va schimba (sau cel puțin va fi adaptată) la o credință ulterioară .
Acest lucru este util pentru înțelegerea incertitudinii sau atunci când lucrați cu multe date zgomotoase, cum ar fi optimizarea ratei de conversie pentru comerțul electronic și în învățarea automată.
Să ne imaginăm asta:
Să spunem, de exemplu, că urmărești o cursă cu cărucioarele de la o facultate și apoi un spectator entuziasmat te provoacă la pariu că tipul în tricou roșu care o poartă cu doamna într-o cămașă verde va câștiga. Gândește-te la asta și contrazici că tipul cu jacheta neagră și fata cu hanoracul negru vor câștiga în schimb.

Un alt spectator deasupra capului și ți-a șoptit un pont: „Băiatul cu tricoul roșu a câștigat ultimele 3 curse din 4.” Ce se întâmplă cu pariul tău? Nu mai ești prea sigur, nu?
Să presupunem că ai aflat și că ultima dată când tipul cu jacheta neagră și-a purtat ochelarii de soare norocoși, a câștigat. Și când nu l-a purtat, a câștigat tipul cu tricoul roșu.
Astăzi, vezi că tipul cu jacheta neagră poartă acei ochelari. Convingerea ta se schimbă din nou. Acum ai mai multă încredere în pariul tău, nu? În această poveste, ți-ai actualizat credința de fiecare dată când ai primit dovezi de date noi. Aceasta este abordarea bayesiană.
Povestea originii bayesiene
Când reverendul Thomas Bayes s-a gândit pentru prima dată la teoria sa, el nu a considerat că este demnă de publicare. Așadar, a rămas în notele sale timp de peste un deceniu. Când familia lui i-a cerut lui Richard Price să-și parcurgă notele, Price a descoperit notele care au stat la baza teoremei lui Bayes.
A început cu un experiment de gândire pentru Bayes. S-a gândit să stea cu spatele la o masă perfect plată și pătrată și să pună un asistent să arunce o minge pe masă.
Mingea ar putea ateriza oriunde pe masă, dar Bayes a crezut că ar putea ghici unde actualizându-și presupunerile cu informații noi. Când mingea a aterizat pe masă, el i-ar fi cerut asistentului să-i spună dacă a aterizat în stânga sau în dreapta, în fața sau în spatele locului în care a aterizat mingea anterioară.
El a notat asta și a ascultat când mai multe mingi aterizau pe masă. Cu informații suplimentare de genul acesta, a descoperit că ar putea îmbunătăți acuratețea presupunerilor sale cu fiecare aruncare. Acest lucru a adus ideea de a ne actualiza înțelegerea pe măsură ce am obținut mai multe dovezi din observație.
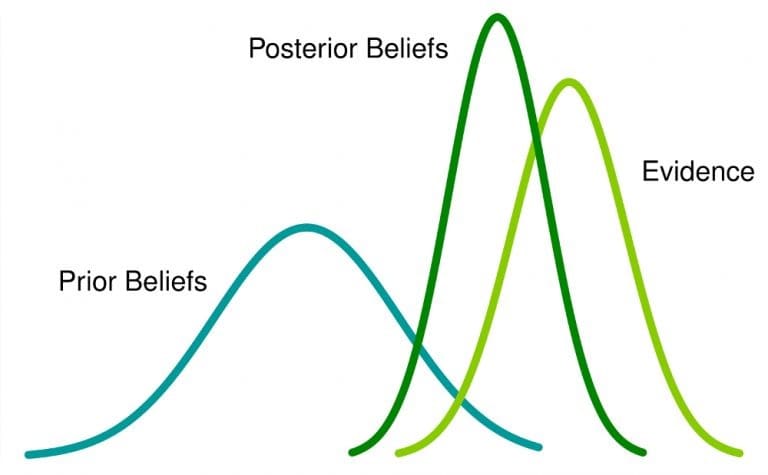
Abordarea bayesiană a analizei datelor este aplicată în diverse domenii, cum ar fi știința și inginerie, și include chiar și sportul și dreptul.
În experimentele online controlate randomizate, în special testarea A/B, puteți utiliza abordarea bayesiană în 4 pași:
- Identificați distribuția dvs. anterioară.
- Alegeți un model statistic care să reflecte convingerile dvs.
- Rulați experimentul.
- După observație, actualizați-vă convingerile și calculați o distribuție posterioară.
Vă actualizați convingerile folosind un set de reguli numit algoritm bayesian.
Un exemplu de statistică bayesiană aplicată testării A/B
Să ilustrăm un exemplu de testare Bayesian A/B.
Imaginați-vă că am efectuat un simplu test A/B pe butonul CTA al unui magazin Shopify. Pentru „A”, folosim „Adaugă în coș”, iar pentru „B”, folosim „Adaugă în coșul tău”.
Iată cum va aborda un frecventist testul.
Există două lumi alternative: una în care A și B nu sunt diferite, astfel încât testul nu va arăta nicio diferență în rata de conversie. Aceasta este ipoteza nulă. Și în cealaltă lume, există o diferență, așa că un buton va funcționa mai bine decât celălalt.
Frecventistul va presupune că trăim în lumea 1 unde nu există nicio diferență în butoanele CTA, adică presupunând că ipoteza nulă este adevărată. Și apoi vor încerca să demonstreze că este greșit la un nivel predeterminat de certitudine numit nivel de semnificație.
Dar așa va aborda un bayesian același test:
Ei încep cu convingerea anterioară că ambele butoane A și B au șanse egale de a produce o rată de conversie între 0 și 100%. Așadar, există o egalitate de butoane chiar de la capăt - ambii au șanse de 50% să fie cei mai performanti.
Apoi începe testul și se strâng datele. Din observarea noilor informații, testerii Bayesian A/B își vor actualiza cunoștințele. Deci, dacă B promite, ei pot ajunge la o credință posterioară bazată pe acea observație care spune: „B are șanse de 61% să-l învingă pe A”.
Există diferențe de bază între cele două metode.
De aceea, este important pentru noi să păstrăm o abordare imparțială a testării Bayesian A/B.
Majoritatea instrumentelor de testare Bayesian A/B – poate în scopuri de marketing – adoptă o atitudine anti-frecventă extremă și susțin argumentul că Bayesian este mai bine să vă spună care variantă este mai „profitabilă”.
Dar o singură abordare statistică a testării A/B deține drepturile exclusive asupra informațiilor?
Dacă se împinge mai departe argumentul bayesian, ei se pot confrunta cu studii în care respondenții spun că vor să știe care este cel mai bun curs de acțiune sau că doresc să maximizeze profiturile sau ceva similar. Acest lucru pune întrebarea ferm pe teritoriul teoretic al deciziei - ceva în care nici inferența bayesiană, nici inferența frecventistă nu pot avea un cuvânt direct de spus.
Georgi Georgiev, creatorul Analytics-toolkit.com și autorul cărții „Metode statistice în testarea A/B online”
Vom face o scurtă scufundare în aceste detalii în secțiunile următoare. Deocamdată, să facem restul acestui primer ușor de înțeles.
Un scurt glosar al termenilor bayesieni care contează pentru testerii A/B
Inferența Bayesiană
Inferența bayesiană este actualizarea probabilității pentru o ipoteză cu date noi. Este construit în jurul credințelor și probabilităților.
Inferența bayesiană folosește probabilitatea condiționată pentru a ne ajuta să înțelegem modul în care datele ne afectează convingerile. Să presupunem că începem cu o credință anterioară că cerul este roșu. După ce ne uităm la unele date, ne-am da seama în curând că această credință anterioară este greșită. Așadar, efectuăm o actualizare bayesiană pentru a îmbunătăți modelul nostru incorect despre culoarea cerului, ajungând la o credință posterioară mai precisă .
Michael Berk în Towards Data Science
Probabilitate condițională
Probabilitatea condiționată este probabilitatea unui eveniment dat fiind că a avut loc un alt eveniment. Adică probabilitatea lui A în condiția B.
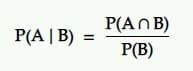
Traducere: Probabilitatea ca un eveniment A să se întâmple având în vedere un alt eveniment B este egală cu probabilitatea ca B și A să se întâmple împreună împărțită la probabilitatea evenimentului B.
Distribuția probabilității/Distribuția probabilității
Distribuțiile de probabilitate sunt distribuții care arată cât de probabil că datele dvs. vor lua o anumită valoare.
Acolo unde datele dvs. pot lua mai multe valori, de exemplu, o categorie precum culorile care ar putea fi gri, roșu, portocaliu, albastru etc., distribuția dvs. este multinomială. Pentru un set de numere, distribuția poate fi normală. Și pentru valorile datelor care ar putea fi fie da/nu, fie adevărat/fals, ar fi binom.
Distribuția anterioară a credinței
Sau distribuția de probabilitate anterioară, numită pur și simplu anterioară, exprimă credința dvs. înainte de a obține dovezi de date noi. Deci, este o expresie a credinței tale inițiale pe care o vei actualiza după ce ai luat în considerare unele dovezi, folosind analiza bayesiană (sau inferența).
Conjugarea
În primul rând, conjugatul se referă la unirea, de obicei în perechi. În teoria probabilității Bayesiană, conjugarea presupune că priorul este conjugat cu probabilitatea.
Dacă posteriorul are aceeași formă funcțională ca anterioară, atunci priorul este conjugat cu funcția de probabilitate. Aceasta arată cum funcția de probabilitate actualizează distribuția anterioară.
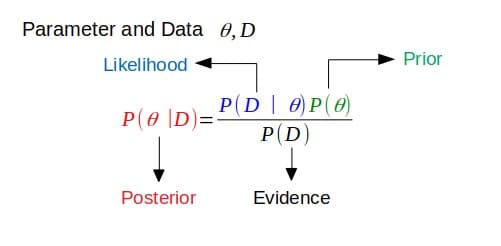
Conjugați Priori
Aceasta este legată de definiția de mai sus. Dacă posteriorul este în aceeași familie de distribuție de probabilitate (sau are aceeași formă funcțională) ca și distribuția de probabilitate anterioară, atunci anterioară și posterioară sunt distribuții conjugate. În acest caz, priorul este numit priorul conjugat pentru funcția de probabilitate.
Ele pot fi subiective (pe baza cunoștințelor experimentatorului), obiective și informative (pe baza datelor istorice) sau neinformative.
Funcția de pierdere
O funcție de pierdere este o modalitate de a cuantifica pierderea prin măsurarea cât de proastă este estimarea noastră actuală. Ne ajută să minimizăm pierderile pentru testarea ipotezelor, mai ales atunci când exprimăm o inferență care se află într-o gamă de valori probabile și să sprijinim luarea deciziilor cu rezultatele testelor noastre.
Acum, asta e din drum, putem merge mai departe.
Dacă ai fost în jurul blocului de ceva vreme, probabil că ai întâlnit mai mult decât câteva meme-uri cu statistici Frequentist vs Bayesian.

Ambele părți par să caute răspunsuri din direcții opuse, dar este chiar așa? Pentru a înțelege mai bine acest lucru (în timp ce rămânem imparțiali), haideți să vizităm tabăra Frequentiștilor.
Ce este statistica frecventistă?
Aceasta este prima tehnică inferențială pe care majoritatea oamenilor o învață în statistică. Statisticile frecventiste calculeaza probabilitatea ca un eveniment (ipoteza) sa apara frecvent in aceleasi conditii.
Testarea ipotezei A/B folosind abordarea frecventistă urmează acești pași:
- Declară unele ipoteze. De obicei, ipoteza nulă este că noua variantă „B” nu este mai bună decât originalul „A”, în timp ce ipoteza alternativă declară contrariul.
- Determinați în avans dimensiunea eșantionului utilizând un calcul statistic al puterii , cu excepția cazului în care utilizați abordări de testare secvențială. Utilizați un calculator pentru dimensiunea eșantionului care ia în considerare puterea statistică, rata de conversie curentă și efectul minim detectabil.
- Rulați testul și așteptați ca fiecare variație să fie expusă la dimensiunea eșantionului predeterminată.
- Calculați probabilitatea de a observa un rezultat cel puțin la fel de extrem ca datele din ipoteza nulă (valoarea p). Respingeți ipoteza nulă și implementați noua variantă în producție dacă valoarea p < 5%.
Cum se compară asta cu Bayesian? Sa vedem…
Testare Bayesian vs Frequentist A/B
Aceasta este o dezbatere notorie oriunde este folosită inferența statistică. Și să fiu sincer, este inutil. Ambele au meritele lor și cazurile în care sunt cea mai bună metodă de utilizat.
Spre deosebire de ceea ce vă vor face să credeți majoritatea promotorilor din ambele tabere, ei sunt similari în mai multe moduri și niciunul nu se apropie de adevăr decât celălalt – deși abordările lor diferă.
Când este aplicată testării A/B, de exemplu, nicio metodă specifică nu vă va oferi o predicție absolută și precisă în ceea ce privește cursul de acțiune care va determina creșterea afacerii. În schimb, testarea A/B vă ajută să eliminați riscul din luarea deciziilor.
Indiferent de modul în care îți analizezi datele – folosind abordări bayesiene sau frecventiste – poți face mișcări cu un anumit nivel de siguranță că ai dreptate.
Și din acest motiv, ambele modele statistice sunt valabile. Bayesianul poate avea un avantaj de viteză, dar este mai solicitant din punct de vedere computațional decât Frequentist.
Vezi și alte diferențe...
Cadrul frecventist
Cei mai mulți dintre noi sunt familiarizați cu abordarea frecventistă din cursurile introductive de statistică. Am definit metodologia de mai sus - de la declararea ipotezei nule, determinarea dimensiunii eșantionului, colectarea datelor printr-un experiment randomizat și, în final, observarea unui rezultat semnificativ statistic.
În Frecventism, considerăm probabilitatea ca fiind legată în mod fundamental de frecvențele evenimentelor repetate. Deci, într-o aruncare corectă de monede, un frecventist crede că, dacă ghicește suficient de des, va obține capul corect în 50% din timp și la fel și pentru cozi.
Mentalitate frecventistă: „Dacă repet experimentul în aceleași condiții iar și iar, care sunt șansele ca metoda mea să obțină răspunsul corect?”
Cadrul Bayesian
În timp ce abordarea frecventistă tratează parametrul populației pentru fiecare variantă ca o constantă (necunoscută), abordarea bayesiană modelează fiecare valoare a parametrului ca o variabilă aleatorie cu o anumită distribuție de probabilitate.
Aici, calculați direct distribuțiile de probabilitate (și, prin urmare, valorile așteptate) pentru parametrii de interes.
Și pentru a modela distribuția probabilității pentru fiecare variantă, ne bazăm pe regula lui Bayes pentru a combina rezultatele experimentului cu orice cunoștințe anterioare pe care le avem despre metrica de interes. Putem simplifica calculele utilizând un prior conjugat.
Alex Birkett a rezumat algoritmul bayesian astfel:
- Definiți distribuția anterioară care încorporează convingerile dvs. subiective despre un parametru. Priorul poate fi neinformativ sau informativ.
- Adunați date.
- Actualizați distribuția anterioară cu datele utilizând teorema lui Bayes (deși puteți avea metode bayesiene fără utilizarea explicită a regulii lui Bayes - vezi Bayesian neparametric) pentru a obține o distribuție posterioară. Distribuția posterioară este o distribuție de probabilitate care reprezintă convingerile dvs. actualizate despre parametru după ce ați văzut datele.
- Analizați distribuția posterioară și rezumați-o (medie, mediană, sd, cuantile...).
Pe scurt, experimentatorul bayesian se concentrează pe propria lor perspectivă și pe ce înseamnă probabilitatea pentru ei. Opinia lor evoluează cu datele observate. Frecvențiștii, pe de altă parte, cred că răspunsul corect este acolo undeva.

Înțelegeți că dezbaterea Frequentist vs Bayesian nu afectează atât de mult analiza post-testare A/B. Diferențele majore dintre cele două tabere sunt mai mult legate de ceea ce poate fi testat.
Statisticile probabilităților nu sunt, în general, utilizate în mare măsură în analizele ulterioare. Argumentul bayesian-frecventist este mai aplicabil în ceea ce privește alegerea variabilelor de testat în paradigma A/B, dar chiar și acolo cei mai mulți testeri A/B încalcă al naibii ipotezele de cercetare, probabilitatea și intervalele de încredere .
Dr. Rob Balon la CXL
Georgi detaliază în continuare:
Există mai multe calculatoare bayesiene online și cel puțin un furnizor important de software de testare A/B care aplică un motor statistic bayesian, care folosesc toate așa-numitele a priori non-informative (un nume puțin greșit, dar să nu mai săpăm în asta). În cele mai multe cazuri, rezultatele acestor instrumente coincid numeric cu rezultatele unui test frecventist pe aceleași date. Să presupunem că instrumentul Bayesian va raporta ceva de genul „probabilitate de 96% ca B să fie mai bun decât A”, în timp ce instrumentul frecventist va produce o valoare p de 0,04, care corespunde unui nivel de încredere de 96%.
Într-o situație ca cea de mai sus, care este mult mai comună decât ar dori unii să admită, ambele metode vor duce la aceeași inferență și nivelul de incertitudine va fi același, chiar dacă interpretarea este diferită.
Ce ar spune un bayesian despre acest rezultat? Transformă valoarea p într-o probabilitate posterior adecvată atunci când vizualizați un scenariu în care nu există informații prealabile? Sau sunt toate aceste aplicații ale testelor bayesiene greșite pentru utilizarea unui prealabil non-informativ în sine?
Chiar nu este nevoie să alegeți o tabără și să găsiți un loc în spatele acoperișului pentru a arunca cu pietre în cealaltă tabără. Există chiar dovezi că ambele cadre produc aceleași rezultate. Indiferent de drumul pe care îl alegeți, probabil că destinația va fi aceeași. Depinde de cum poți ajunge acolo cu Frequentist vs Bayesian.
De exemplu:
- Există date care arată că testarea bayesiană este mai rapidă și alegerea preferată pentru experimentele interactive:
Deoarece paradigma bayesiană permite experimentatorilor să cuantifice în mod oficial credința și să încorporeze cunoștințe suplimentare, este mai rapidă decât analiza statistică tradițională.
Într-o simulare de testare Bayesian A/B, când criteriul de decizie a fost ajustat (adică creșterea toleranței la greșeli), 75% dintre experimente s-au încheiat în 22,7% din observațiile cerute de abordarea tradițională (la un nivel de semnificație de 5%). Și a înregistrat doar 10% eroare de tip II. - Bayesianul este, de asemenea, considerat mai iertător, în timp ce Frequentist este opus riscului:
În timp ce multe teste Frequentist folosesc o semnificație statistică de 95%, bayesienii pot fi mulțumiți cu mai puțin de atât. Dacă o variantă are o șansă de 78% să bată controlul, în funcție de pierderea așteptată, ar putea fi o decizie corectă să implementeze varianta respectivă.
Dacă greșești și pierderea așteptată este mai mică de un procent, aceasta este un prejudiciu destul de nesemnificativ pentru multe companii. Această abordare neplăcută poate fi mai potrivită pentru luarea rapidă a deciziilor în scenarii cu risc foarte scăzut. - Cu toate acestea, simulările și calculele bayesiene sunt grele de calcul:
Frequentist, pe de altă parte, se bazează pe pix și hârtie. Avertisment: dacă instrumentul dvs. de testare A/B folosește bayesian și nu știți ce presupuneri sunt adăugate datelor dvs., atunci nu vă puteți baza pe „răspunsul” pe care vi-l oferă furnizorul. Se ia cu un praf de sare. Și fă-ți propria analiză.
Nu totul este soare și curcubeu cu Bayesian. După cum subliniază Georgi cu această listă de întrebări:
- „Doriți să obțineți produsul dintre probabilitatea anterioară și funcția de probabilitate?”
- „Doriți ca rezultat un amestec de probabilități anterioare și date?”
- „Vrei ca credințe subiective amestecate cu datele să producă rezultatul?” (dacă utilizați antecedente informative)
- „V-ar fi confortabil să prezentați statistici în care există informații anterioare presupuse a fi foarte sigure amestecate cu datele reale?”
Acestea sunt toate aspectele statisticii bayesiene, în termeni profani.
Ce vă spun de fapt statisticile bayesiene în testarea A/B?
V-ați conceput testul A/B pentru a oferi informații despre modul în care o modificare vă afectează valoarea de interes, cum ar fi rata de conversie sau venitul per vizitator.
Când utilizați un instrument care funcționează cu statistici bayesiene, este important să înțelegeți ce înseamnă rezultatele dvs. deoarece „B este câștigătorul” nu înseamnă exact ceea ce cred majoritatea oamenilor că face.
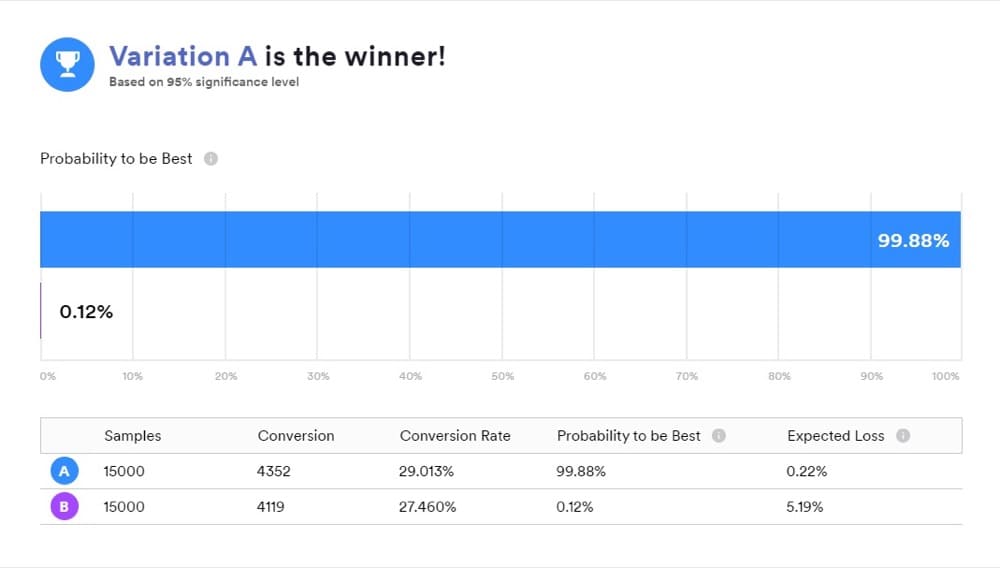
Este o modalitate convenabilă de a prezenta rezultatele, dar nu asta a dezvăluit testul tău. În schimb, răspunsurile pe care le doriți sunt în comparații posterioare ale „A” și „B”.
Iată cele 3 metode de comparare:
Probabilitatea de a fi cel mai bun (P2BB)
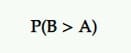
Aceasta este probabilitatea care declară un câștigător în testarea Bayesian A/B.
Varianta cu probabilitatea de a fi cea mai bună este cea cu cea mai mare probabilitate de a continua să o depășească pe cealaltă.
Acesta este calculat dintr-un set de mostre posterioare ale măsurătorii de interes de la original și contestator.
Deci, dacă B are cea mai mare probabilitate de a vă crește ratele de conversie, de exemplu, B este declarat câștigător.
Creștere așteptată
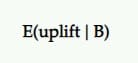
Deci, dacă B este câștigătorul, cât de mult ar trebui să ne așteptăm de la el? Va continua să ofere aceleași rezultate pe care le-am văzut în test?
Aceasta este ideea pe care dorește să o ofere creșterea așteptată. Creșterea așteptată a alegerii lui B față de A, având în vedere un set de eșantioane posterioare, este definită ca intervalul credibil (sau media) a creșterii procentuale.
În testarea A/B, de obicei comparăm acest lucru ca challenger față de control. Deci, dacă contestatorul a pierdut, este reprezentat în valori negative (cum ar fi -11,35%) și valori pozitive (cum ar fi +9,58%) dacă a câștigat.
Pierderea așteptată
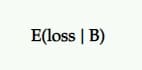
Deoarece nu există o probabilitate de 100% ca B să fie mai bun decât A, atunci există șansa de a înregistra o pierdere dacă alegeți B în locul lui A. Aceasta este reprezentată ca pierdere așteptată și, la fel ca în cazul creșterii așteptate, este exprimată din punctul de vedere al contestatorului împotriva controlului.
Îți spune riscul de a-ți alege varianta P2BB (adică câștigătorul declarat).
Înainte de a ne arunca în mituri, un mare mulțumire legendei analitice Georgi Georgiev. Analizele sale aprofundate ale inferenței frecventiste vs bayesiene și probabilității și statisticilor bayesiene în testarea A/B au inspirat secțiunea următoare.
Mituri în jurul statisticilor bayesiene de evitat
Cu o rivalitate care este aproape la fel de veche pe atât de inutilă, dezbaterea Bayesian vs Frequentist a adunat o mulțime de contribuții - și a dat naștere la o mulțime de mituri.
Cel mai mare dintre aceste mituri (mitul #2) este promovat de furnizorii de instrumente de testare A/B pentru a vă spune de ce o abordare este mai bună decât cealaltă.
Dar după ce ai citit secțiunile de mai sus, știi mai bine.
Să dezvăluim găurile din aceste mituri.
Mitul #1: Bayesienii își exprimă ipotezele, frecvențiștii nu
Acest lucru sugerează că bayesienii fac ipoteze sub formă de distribuții anterioare și acestea sunt deschise pentru evaluare. Dar frecvențiștii fac presupuneri care sunt ascunse în mijlocul matematicii.
De ce este greșit: bayesienii și frecvențiștii fac ipoteze de bază similare, singura diferență este că bayesienii fac ipoteze suplimentare - pe lângă matematică.
Modelele frecventiste folosesc ipoteze în matematică, cum ar fi forma distribuției, omogenitatea sau eterogenitatea efectului între observații și independența observației. Și nu sunt ascunse. De fapt, ele sunt discutate pe scară largă în comunitatea statistică și menționate pentru fiecare test statistic frecventist.
Adevărul: frecvențiștii își exprimă în mod explicit ipotezele și fac un pas mai departe pentru a testa ipotezele: teste pentru normalitate, test de bunăstare a potrivirii (sub care avem testul de nepotrivire a raportului eșantionului) și multe altele.
Mitul #2. Metodele bayesiene vă oferă răspunsurile pe care le doriți de fapt
Concepția greșită aici este că valorile p și intervalele de încredere nu spun testatorilor ceea ce vor să știe, în timp ce probabilitățile posterioare și intervalele credibile spun. Oamenii vor să știe lucruri precum
- Probabilitatea ca B să o depășească pe A și
- Probabilitatea ca rezultatul să nu fie o coincidență.
Valorile P și testele de ipoteză (inferența directă) nu oferă aceste informații, dar inferența inversă o oferă.
De ce este greșit: aceasta este o problemă de lingvistică. În general, atunci când cei care nu sunt statisticieni folosesc termeni precum „probabilitate”, „șansă” și „probabilitate”, ei nu îi folosesc având în vedere sensul lor tehnic. Sondați mai profund și veți descoperi că sunt la fel de confuzi în ceea ce privește inferența inversă, precum și în ceea ce privește inferența dreaptă.
Potrivit lui Georgi Georgiev, întrebări ca acestea încep să apară:
- „ Ce este o probabilitate anterioară? Ce valoare aduce?”
- „Ce este o funcție de probabilitate?”
- „Ce probabilitate „anterior”, nu am date anterioare?”
- „Cum apăr alegerea unei probabilități anterioare?”
- „Există o modalitate de a comunica exact ceea ce spun datele, fără niciunul dintre aceste amestecuri?”
Adevărul: ar trebui să existe o perspectivă mai bună a ceea ce testerii doresc să știe, nu asupra interpretării greșite a termenilor tehnici. Valorile P, intervalele de încredere și altele vă spun cât de bine sunt analizate rezultatele cu datele adunate. Acestea au oferit o măsură de certitudine fără influența unor ipoteze anterioare subiective, netestate.
Mitul #3: Inferența bayesiană vă ajută să comunicați incertitudinea mai bine decât inferența frecventistă
Pentru că rezultatele testelor produc mai multe perspective „semnificative”.
De ce este greșit: Atât abordările frecventiste, cât și cele bayesiene au instrumente similare pentru a vă ajuta să comunicați certitudinea și rezultatele testului dvs. A/B.
| frecventist | Bayesian | ||||||||||
| ● Estimări punctuale | ● Estimări punctuale | ||||||||||
| ● Valori P | ● Intervale credibile | ||||||||||
| ● Intervale de încredere | ● Factorii Bayes | ||||||||||
| ● Curbe P-valoare | ● Distribuții posterioare (realizează aceeași sarcină ca curbele frecventiste) | ||||||||||
| ● Curbe de încredere | |||||||||||
| ● Curbele de severitate etc. |
Adevărul: totul depinde de cum le folosești. Ambele metode sunt la fel de eficiente în comunicarea incertitudinii. Cu toate acestea, există diferențe în modul în care prezintă măsura incertitudinii.
Mitul #4. Rezultatele testării Bayesian A/B sunt imune la peeking
Unii statisticieni bayesieni susțin că poți opri un test bayesian odată ce vezi un „câștigător clar” și nu are nicio diferență pentru rezultatul final.
Probabil știți că acest lucru este inacceptabil în testele Frequentist, așa că este considerat un dezavantaj în comparație cu Bayesian. Dar este cu adevărat?
De ce este greșit: Într-un studiu din 1969 din Jurnalul Societății Regale de Statistică intitulat „Teste de semnificație repetate asupra datelor acumulate”, Armitage și colab. a arătat cum oprirea opțională bazată pe rezultate crește probabilitatea de eroare.
Nu poți să te oprești pur și simplu când observi un câștigător, să-ți actualizezi posteriorul și să-l folosești ca următor anterior fără a ajusta modul în care funcționează analiza bayesiană.
Adevărul: Peeking-ul afectează inferența bayesiană la fel de mult ca și Frequentist (dacă vrei să o faci corect).
Mitul #5. Statisticile Frecventist sunt ineficiente, deoarece trebuie să așteptați o dimensiune fixă a eșantionului
Unii membri ai comunității CRO cred că testele statistice frecventiste trebuie să fie efectuate cu o dimensiune a eșantionului fixă, predeterminată, altfel rezultatele sunt invalide.
Ca urmare, așteptați mai mult decât este necesar pentru a obține rezultatele dorite.
De ce este greșit: statisticile frecventiste nu au fost folosite în acest fel de aproximativ șapte decenii. Cu testele secvențiale frecventiste, nu aveți nevoie de o durată fixă predeterminată.
Adevărul: testele secvențiale, care sunt mai populare astăzi, necesită o dimensiune maximă a eșantionului pentru a echilibra erorile de tip I și de tip II, dar dimensiunea efectivă a eșantionului utilizat variază de la caz la caz, în funcție de rezultatul observat.
Deci, ar trebui să alegeți Bayesian sau Frequentist? Există un loc pentru amândoi.
Nu este nevoie să alegeți o parte. Ambele metode au locul lor. De exemplu, un proiect pe termen lung care utilizează antecedente actualizate și are nevoie de rezultate rapide este mai bine cu abordarea bayesiană.
Metoda Frequentist, pe de altă parte, este cea mai potrivită pentru proiectele care necesită o cantitate semnificativă de repetabilitate a rezultatelor lor. Cum ar fi software-ul de scriere pe care îl vor folosi mulți oameni cu multe seturi de date.
După cum spune Cassie Kozyrkov, șeful departamentului de informații pentru decizii la Google, „statistica este știința de a vă răzgândi în condiții de incertitudine”.
În videoclipul ei rezumat Bayesian vs Frequentist Statistics, ea a spus:
„Puteți să luați acea dezbatere frecventistă și bayesiană și să reduceți totul la ceea ce vă răzgândiți. Frecvențiștii își răzgândesc părerea cu privire la acțiuni, au o acțiune implicită preferată - poate că nu au nicio convingere - dar au o acțiune care le place în ignoranță și apoi întreabă: „Dovezile mele [sau datele] mă răzgândesc despre acea acțiune?” „Mă simt ridicol făcând asta pe baza dovezilor mele?”
Bayesienii, pe de altă parte, își răzgândesc într-un mod diferit. Ei încep cu o opinie, o opinie personală exprimată matematic, numită anterioară, apoi se întreabă: „Care este opinia sensibilă pe care ar trebui să o am după ce încorporez niște dovezi?” Și astfel, frecvențiștii își răzgândesc părerea despre acțiuni, bayesienii își schimbă părerea despre credințe.
Și, în funcție de modul în care doriți să vă încadrați luarea deciziilor, s-ar putea să preferați să mergeți cu o tabără față de cealaltă.”
În cele din urmă, cu toții ne îndreptăm către concluzii similare - diferența este în modul în care vi se prezintă aceste concluzii.
Dacă inferența frecventistă și bayesiană ar fi funcții de programare, intrările fiind probleme statistice, atunci cele două ar fi diferite în ceea ce returnează utilizatorului. Funcția de inferență frecventistă ar returna un număr, reprezentând o estimare (de obicei, o statistică rezumată, cum ar fi media eșantionului etc.), în timp ce funcția Bayesiană ar returna probabilități.
Extras din cartea „Probabilistic Programming & Bayesian Methods for Hackers
Ceea ce nu este tocmai corect este afirmația că unul dă rezultate mai practice decât cealaltă.
Cheie la pachet
Statisticile bayesiene în testarea A/B constă din 4 pași distincti:
- Identificați distribuția dvs. anterioară
- Alegeți un model statistic care să reflecte convingerile dvs
- Rulați experimentul
- Utilizați rezultatele pentru a vă actualiza convingerile și pentru a calcula o distribuție posterioară
Rezultatele tale te vor îndrepta către probabilități perspicace. Deci, veți ști care variantă are cea mai mare probabilitate de a fi cea mai bună, pierderea așteptată și creșterea așteptată.
Acestea sunt de obicei interpretate pentru dvs. de majoritatea instrumentelor de testare A/B folosind statistici bayesiene. Dar un experimentator amănunțit va efectua o analiză post-test pentru a înțelege mai bine aceste rezultate.
Pentru că ai ajuns până aici, iată un fapt amuzant pentru tine: știi portretul lui Thomas Bayes cu care toată lumea este familiarizată? Aceasta:

Nimeni nu este 100% sigur că acesta este el.