Erros Tipo I e Tipo II: Os Erros Inevitáveis ​​na Otimização

Os erros do tipo I e do tipo II acontecem quando você identifica erroneamente os vencedores em seus experimentos ou não os identifica. Com os dois erros, você acaba indo com o que parece funcionar ou não. E não com os resultados reais.

A interpretação errônea dos resultados dos testes não resulta apenas em esforços de otimização mal orientados, mas também pode inviabilizar seu programa de otimização a longo prazo.

O melhor momento para detectar esses erros é antes mesmo de cometê-los! Então, vamos ver como você pode evitar erros do tipo I e do tipo II em seus experimentos de otimização.

Mas antes disso, vejamos a hipótese nula... porque é a rejeição ou não rejeição errônea da hipótese nula que causa os erros tipo I e tipo II .

A hipótese nula: H0

Quando você cria a hipótese de um experimento, você não pula diretamente para sugerir que a mudança proposta moverá uma determinada métrica.

Você começa dizendo que a mudança proposta não afetará a métrica em questão - que eles não estão relacionados.

Esta é a sua hipótese nula (H0). H0 é sempre que não há mudança. Isso é o que você acredita, por padrão... até (e se) seu experimento o refutar.

E sua hipótese alternativa (Ha ou H1) é que há uma mudança positiva. H0 e Ha são sempre opostos matemáticos. Ha é aquela em que você espera que a mudança proposta faça a diferença, é sua hipótese alternativa - e é isso que você está testando com seu experimento.

Assim, por exemplo, se você deseja realizar um experimento em sua página de preços e adicionar outro método de pagamento a ele, primeiro forma uma hipótese nula dizendo: O método de pagamento adicional não terá impacto nas vendas. Sua hipótese alternativa seria: O método de pagamento adicional VAI aumentar as vendas.

Executar um experimento é, de fato, desafiar a hipótese nula ou o status quo.

Os erros do tipo I e do tipo II acontecem quando você rejeita erroneamente ou deixa de rejeitar a hipótese nula.

Entendendo os Erros Tipo I

Os erros do tipo I são conhecidos como falsos positivos ou erros alfa.

Em uma instância de erro do tipo I de teste de hipóteses, seu teste ou experimento de otimização * PARECE SER BEM-SUCEDIDO* e você (erroneamente) conclui que a variação que está testando está sendo diferente (melhor ou pior) do que o original.

Nos erros do tipo I, você vê elevações ou quedas - que são apenas temporárias e provavelmente não se manterão a longo prazo - e acabam rejeitando sua hipótese nula (e aceitando sua hipótese alternativa).

Rejeitar erroneamente a hipótese nula pode acontecer por várias razões, mas a principal é a prática de espiar (ou seja, olhar seus resultados no ínterim ou quando o experimento ainda está em execução). E chamar os testes antes que os critérios de parada definidos sejam alcançados.

Muitas metodologias de teste desencorajam a prática de espiar, pois olhar para resultados provisórios pode levar a conclusões erradas, resultando em erros do tipo I.

Veja como você pode cometer um erro do tipo I:

Suponha que você esteja otimizando a página de destino do seu site B2B e suponha que adicionar selos ou prêmios a ela reduzirá a ansiedade de seus clientes em potencial, aumentando assim sua taxa de preenchimento de formulários (resultando em mais leads).

Portanto, sua hipótese nula para este experimento se torna: a adição de selos não afeta o preenchimento de formulários.

O critério de parada para tal experimento é geralmente um determinado período e/ou após X conversões acontecerem no nível de significância estatística definido. Convencionalmente, os otimizadores tentam atingir a marca de confiança estatística de 95% porque isso deixa você com 5% de chance de cometer o erro tipo I, considerado baixo o suficiente para a maioria dos experimentos de otimização. Em geral, quanto maior essa métrica, menores são as chances de cometer erros do tipo I.

O nível de confiança que você almeja determina qual será sua probabilidade de obter um erro tipo I (α).

Portanto, se você almeja um nível de confiança de 95%, seu valor para α se torna 5%. Aqui, você aceita que há 5% de chance de que sua conclusão esteja errada.

Por outro lado, se você usar um nível de confiança de 99% em seu experimento, sua probabilidade de obter um erro do tipo I cai para 1%.

Digamos que, para este experimento, você fique muito impaciente e, em vez de esperar que seu experimento termine, você olhe para o painel da sua ferramenta de teste (espiada!) apenas um dia depois. E você percebe um aumento “aparente” – que sua taxa de preenchimento de formulários aumentou 29,2% com um nível de confiança de 95%.

E BAM…

… você interrompe seu experimento.

… rejeitar a hipótese nula (que os crachás não tiveram impacto nas vendas).

… aceite a hipótese alternativa (que os crachás impulsionaram as vendas).

… e corra com a versão com os distintivos de premiação.

Mas ao medir seus leads ao longo do mês, você descobre que o número é quase comparável ao que você relatou com a versão original. Os distintivos não importavam tanto, afinal. E que a hipótese nula foi provavelmente rejeitada em vão.

O que aconteceu aqui foi que você terminou seu experimento cedo demais e rejeitou a hipótese nula e acabou com um falso vencedor – cometendo um erro do tipo I.

Evitando erros do tipo I em seus experimentos

Uma maneira segura de diminuir suas chances de acertar um erro tipo I é usar um nível de confiança mais alto. Um nível de significância estatística de 5% (traduzindo para um nível de confiança estatística de 95%) é aceitável. É uma aposta que a maioria dos otimizadores faria com segurança porque, aqui, você falhará na improvável faixa de 5%.

Além de definir um alto nível de confiança, é importante executar seus testes por tempo suficiente. As calculadoras de duração de teste podem dizer por quanto tempo você deve executar seu teste (depois de fatorar coisas como um tamanho de efeito especificado, entre outros). Se você deixar um experimento seguir o curso pretendido, reduzirá significativamente suas chances de encontrar o erro tipo 1 (desde que esteja usando um alto nível de confiança). Esperar até que você alcance resultados estatisticamente significativos garante que há apenas uma pequena chance (geralmente 5%) de que você rejeitou a hipótese nula erroneamente e cometeu um erro tipo I. Em outras palavras, use um bom tamanho de amostra porque isso é crucial para obter resultados estatisticamente significativos.

Agora, isso era tudo sobre erros do tipo I que estão relacionados ao nível de confiança (ou significância) em seus experimentos. Mas também há outro tipo de erro que pode se infiltrar em seus testes – os erros do tipo II.

Entendendo os Erros Tipo II

Os erros do tipo II são conhecidos como falsos negativos ou erros Beta.

Em contraste com o erro do tipo I, no caso de um erro do tipo II, o experimento *PARECE SER MAL SUCEDIDO (OU INCONCLUSIVO)* e você (erroneamente) conclui que a variação que está testando não é diferente da original.

Nos erros do tipo II, você não consegue ver as elevações ou quedas reais e acaba não rejeitando a hipótese nula e rejeitando a hipótese alternativa.

Veja como você pode fazer o erro tipo II:

Voltando ao mesmo site B2B de cima…

Então, suponha que desta vez você suponha que adicionar um aviso de conformidade com o GDPR com destaque na parte superior do seu formulário incentivará mais clientes em potencial a preenchê-lo (resultando em mais leads).

Portanto, sua hipótese nula para este experimento se torna: A isenção de responsabilidade de conformidade com o GDPR não afeta os preenchimentos de formulários.

E a hipótese alternativa para o mesmo diz: O aviso de conformidade com o GDPR resulta em mais preenchimentos de formulários.

O poder estatístico de um teste determina quão bem ele pode detectar diferenças no desempenho de suas versões original e desafiadora, caso existam desvios. Tradicionalmente, os otimizadores tentam atingir a marca de 80% de poder estatístico porque quanto maior essa métrica, menores são as chances de cometer erros do tipo II.

O poder estatístico assume um valor entre 0 e 1 (e geralmente é expresso em %) e controla a probabilidade de seu erro tipo II (β); é calculado como: 1 – β

Quanto maior o poder estatístico do seu teste, menor será a probabilidade de encontrar erros do tipo II.

Portanto, se um experimento tem um poder estatístico de 10%, pode ser bastante suscetível a um erro do tipo II. Considerando que, se um experimento tiver um poder estatístico de 80%, será muito menos provável que cometa um erro do tipo II.

Novamente, você executa seu teste, mas desta vez você não percebe nenhum aumento significativo em seus preenchimentos de formulário. Ambas as versões relatam conversões quase semelhantes. Por isso, você interrompe seu experimento e continua com a versão original sem a isenção de responsabilidade de conformidade com o GDPR.

No entanto, à medida que você se aprofunda nos dados de leads do período do experimento, descobre que, embora o número de leads de ambas as versões (a original e a desafiadora) pareça idêntico, a versão GDPR trouxe um aumento bom e significativo no número de leads da Europa. (Claro, você poderia ter usado a segmentação de público para mostrar o experimento apenas para os leads da Europa – mas isso é outra história.)

O que aconteceu aqui foi que você terminou seu teste muito cedo, sem verificar se havia atingido energia suficiente - cometendo um erro do tipo II.

Como evitar erros do tipo II em seus experimentos

Para evitar erros do tipo II, execute testes com alto poder estatístico. Tente configurar seus experimentos para atingir pelo menos 80% da marca de poder estatístico. Este é um nível aceitável de poder estatístico para a maioria dos experimentos de otimização. Com ele, você pode garantir que em pelo menos 80% dos casos, você rejeitará corretamente uma hipótese nula falsa.

Para fazer isso, você precisa olhar para os fatores que contribuem para isso.

O maior deles é o tamanho da amostra (dado um tamanho de efeito observado). O tamanho da amostra está diretamente relacionado ao poder de um teste. Um tamanho de amostra enorme significa um teste de alta potência. Testes de baixa potência são muito vulneráveis ​​a erros do tipo II, pois suas chances de detectar diferenças nos resultados do seu desafiante e das versões originais diminuem bastante, especialmente para MEIs baixos (mais sobre isso abaixo). Portanto, para evitar erros do tipo II, espere que o teste acumule energia suficiente para minimizar os erros do tipo II. Idealmente, para a maioria dos casos, você deseja atingir uma potência de pelo menos 80%.

Outro fator é o efeito mínimo de interesse (MEI) que você segmenta para sua experiência. MEI (também chamado de MDE) é a magnitude mínima da diferença que você gostaria de detectar no seu KPI em questão. Se você definir um MEI baixo (de olho em um aumento de 1,5%, por exemplo), suas chances de encontrar o erro tipo II aumentam porque detectar pequenas diferenças precisa de tamanhos de amostra substancialmente maiores (para obter potência suficiente).

E, finalmente, é importante notar que tende a haver uma relação inversa entre a probabilidade de cometer um erro tipo I (α) e a probabilidade de cometer um erro tipo II (β). Por exemplo, se você diminuir o valor de α para diminuir a probabilidade de cometer um erro do tipo I (digamos que você defina α em 1%, significando um nível de confiança de 99%), o poder estatístico de seu experimento (ou sua capacidade, β , de detectar uma diferença quando ela existe) acaba reduzindo também, aumentando assim sua probabilidade de obter um erro tipo II.

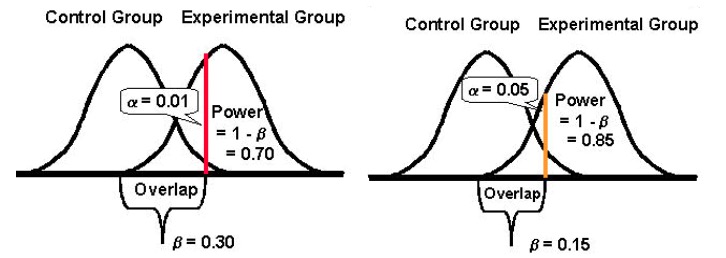
Aceitando melhor qualquer um dos erros: Tipo I e II (e equilibrando-se)

Diminuir a probabilidade de um tipo de erro aumenta a do outro tipo (dado que todo o resto permanece o mesmo).

E então você precisa atender a qual tipo de erro você pode ser mais tolerante.

Cometer um erro do tipo I, por um lado, e implementar uma mudança para todos os seus usuários pode custar conversões e receita – pior, pode ser um assassino de conversão também.

Cometer um erro tipo II, por outro lado, e não lançar uma versão vencedora para todos os seus usuários pode, novamente, custar-lhe as conversões que você poderia ter ganho.

Invariavelmente, ambos os erros têm um custo.

No entanto, dependendo do seu experimento, um pode ser mais aceitável para você do que o outro. Em geral, os testadores encontram o erro tipo I cerca de quatro vezes mais grave do que o erro tipo II .

Se você gostaria de ter uma abordagem mais equilibrada, o estatístico Jacob Cohen sugere que você deve optar por um poder estatístico de 80% que vem com “ um equilíbrio razoável entre o risco alfa e beta. ” (80% de potência também é o padrão para a maioria das ferramentas de teste.)

E no que diz respeito à significância estatística, o padrão é fixado em 95%.

Basicamente, trata-se de compromisso e do nível de risco que você está disposto a tolerar. Se você quisesse realmente minimizar as chances de ambos os erros, poderia optar por um nível de confiança de 99% e um poder de 99%. Mas isso significaria que você estaria trabalhando com tamanhos de amostra impossivelmente grandes por períodos que parecem eternamente longos. Além disso, mesmo assim você estaria deixando alguma margem para erros.

De vez em quando, você vai concluir um experimento de forma errada. Mas isso faz parte do processo de teste — leva um tempo para dominar as estatísticas de teste A/B. Investigar e testar novamente ou acompanhar seus experimentos bem-sucedidos ou fracassados ​​é uma maneira de reafirmar suas descobertas ou descobrir que você cometeu um erro.