Rede Neural de Neurônio Único em Python – Com Intuição Matemática

Vamos construir uma rede simples — muito, muito simples, mas uma rede completa — com uma única camada. Apenas uma entrada – e um neurônio (que também é a saída), um peso, um viés.

Vamos executar o código primeiro e depois analisar parte por parte

Clone o projeto do Github ou simplesmente execute o código a seguir em seu IDE favorito.

Se você precisar de ajuda para configurar um IDE, descrevi o processo aqui.

Se tudo der certo, você obterá esta saída:

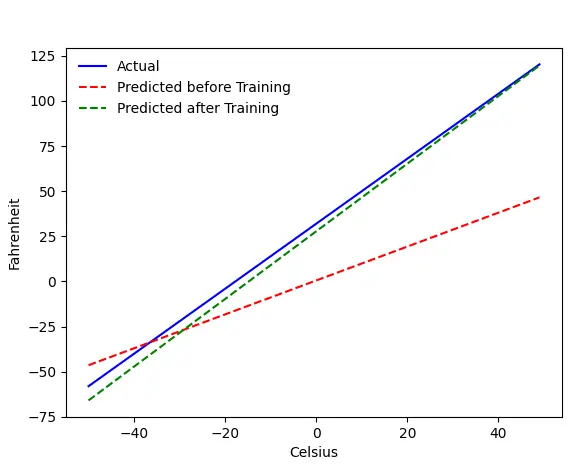
O problema - Fahrenheit de Celsius

Vamos treinar nossa máquina para prever Fahrenheit a partir de Celsius. Como você pode entender pelo código (ou gráfico), a linha azul é a relação real Celsius-Fahrenheit. A linha vermelha é a relação prevista pela nossa máquina de bebés sem qualquer treino. Por fim, treinamos a máquina e a linha verde é a previsão após o treinamento.

Veja Line#65–67 — antes e depois do treinamento, está prevendo usando a mesma função ( get_predicted_fahrenheit_values() ). Então, o que magic train() está fazendo? Vamos descobrir.

Estrutura de rede

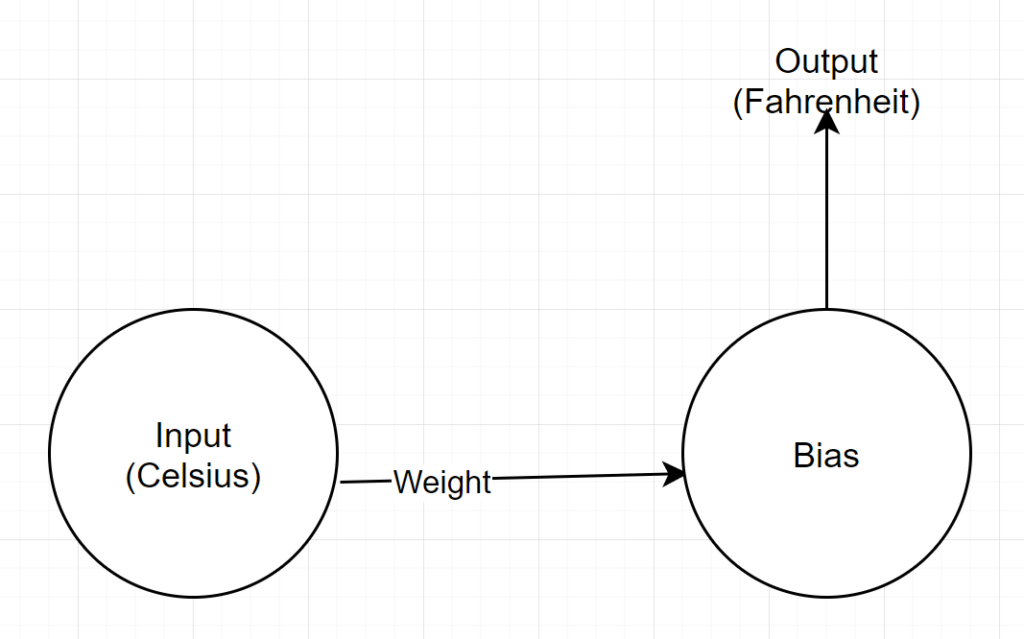
Entrada: Um número que representa celsius

Peso: Um flutuador que representa o peso

Viés: Um float representando viés

Saída: Um float representando Fahrenheit previsto

Então, temos um total de 2 parâmetros - 1 peso e 1 viés

Análise de código

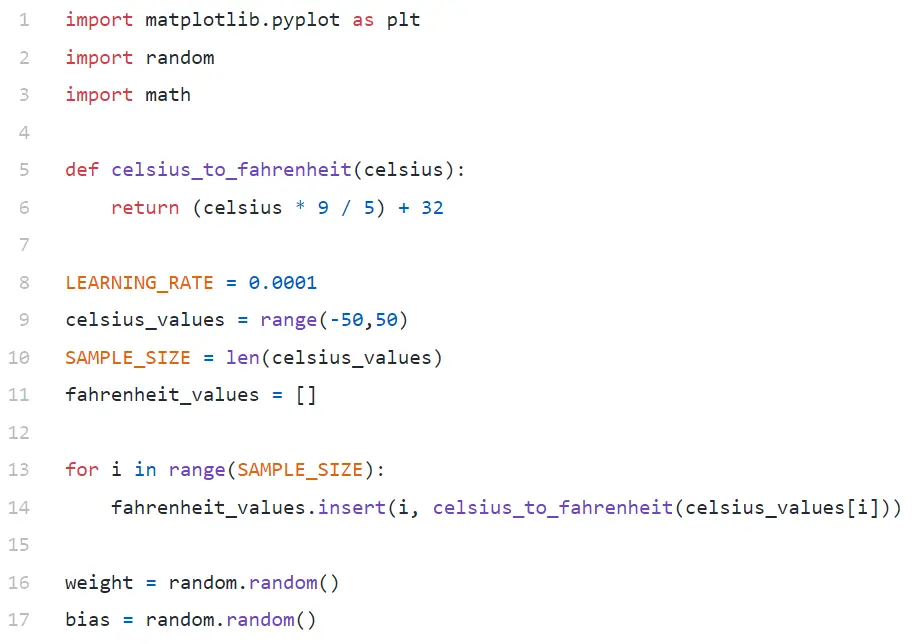
Na linha 9, estamos gerando um array de 100 números entre -50 e +50 (excluindo 50 — a função range exclui o valor do limite superior).

Na linha #11–14, estamos gerando o Fahrenheit para cada valor celsius.

Nas linhas 16 e 17, estamos inicializando o peso e o viés.

Comboio()

Estamos executando 10.000 iterações de treinamento aqui. Cada iteração é composta por:

1. passagem para frente (linha # 57)
2. passagem para trás (linha # 58)
3. update_parameters (Linha nº 59)

Se você é novo em python, pode parecer um pouco estranho para você - funções python podem retornar vários valores como tupla .

Observe que update_parameters é a única coisa que nos interessa. Todo o resto que estamos fazendo aqui é avaliar os parâmetros desta função, que são os gradientes (explicaremos abaixo o que são gradientes) de nosso peso e bias.

1. grad_weight: Um float representando gradiente de peso
2. grad_bias: Um float representando gradiente de viés

Obtemos esses valores chamando para trás, mas requer saída, que obtemos chamando para frente na linha #57.

frente()

Observe que aqui celsius_values ​​e fahrenheit_values ​​são arrays de 100 linhas:

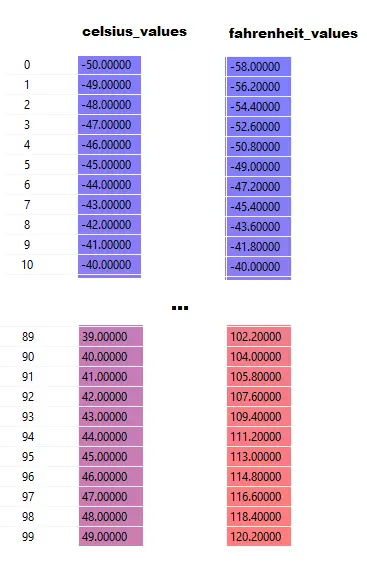
Depois de executar a linha #20–23, para um valor celsius, digamos 42

saída = 42 * peso + polarização

Portanto, para 100 elementos em celsius_values ​​, a saída será uma matriz de 100 elementos para cada valor celsius correspondente.

A linha #25–30 está calculando a perda usando a função de perda Mean Squared Error (MSE), que é apenas um nome chique do quadrado de todas as diferenças dividido pelo número de amostras (100 neste caso).

Pequena perda significa melhor previsão. Se você mantiver a perda de impressão em cada iteração, verá que ela está diminuindo à medida que o treinamento avança.

Por fim, na linha 31, estamos retornando a saída e a perda previstas.

para trás

Estamos apenas interessados ​​em atualizar nosso peso e viés. Para atualizar esses valores, temos que conhecer seus gradientes, e é isso que estamos calculando aqui.

Observe que os gradientes estão sendo calculados na ordem inversa. O gradiente de saída está sendo calculado primeiro e, em seguida, para peso e viés, e por isso o nome “backpropagation”. A razão é que, para calcular o gradiente de peso e viés, precisamos conhecer o gradiente de saída – para que possamos usá-lo na fórmula da regra da cadeia .

Agora vamos dar uma olhada no que é gradiente e regra de cadeia.

Gradiente

Para simplificar, considere que temos apenas um valor de celsius_values ​​e fahrenheit_values ​​, 42 e 107,6 respectivamente.

Agora, o detalhamento do cálculo na Linha 30 se torna:

perda = (107,6 — (42 * peso + viés))² / 1

Como você vê, a perda depende de 2 parâmetros – pesos e viés. Considere o peso. Imagine, inicializamos com um valor aleatório, digamos, 0,8, e após avaliar a equação acima, obtemos 123,45 como valor de perda . Com base nesse valor de perda, você deve decidir como atualizará o peso. Você deve torná-lo 0,9 ou 0,7?

Você precisa atualizar o peso de forma que na próxima iteração você obtenha um valor menor para a perda (lembre-se, minimizar a perda é o objetivo final). Então, se o aumento de peso aumenta a perda, nós a diminuiremos. E se o aumento de peso diminui a perda, vamos aumentá-lo.

Agora, a questão, como sabemos se o aumento de peso aumentará ou diminuirá a perda. É aqui que entra o gradiente . Em termos gerais, gradiente é definido por derivada. Lembre-se de seu cálculo do ensino médio, ∂y/∂x (que é derivada parcial/gradiente de y em relação a x) indica como y mudará com uma pequena mudança em x.

Se ∂y/∂x for positivo, significa que um pequeno incremento em x aumentará y.

Se ∂y/∂x for negativo, significa que um pequeno incremento em x diminuirá y.

Se ∂y/∂x for grande, uma pequena mudança em x causará uma grande mudança em y.

Se ∂y/∂x for pequeno, uma pequena mudança em x causará uma pequena mudança em y.

Então, dos gradientes, obtemos 2 informações. Em qual direção o parâmetro deve ser atualizado (aumento ou diminuição) e quanto (grande ou pequeno).

Regra da cadeia

Informalmente falando, a regra da cadeia diz:

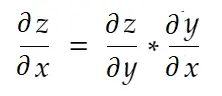
Considere o exemplo de peso acima. Precisamos calcular grad_weight para atualizar esse peso, que será calculado por:

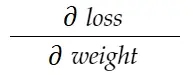
Com a fórmula da regra da cadeia, podemos derivá-la:

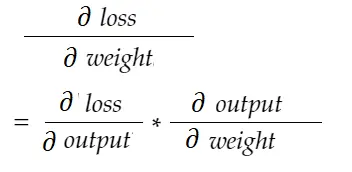
Da mesma forma, gradiente para viés:

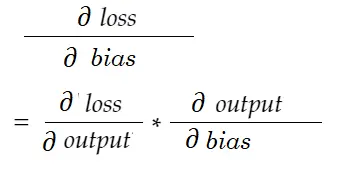
Vamos desenhar um diagrama de dependência.

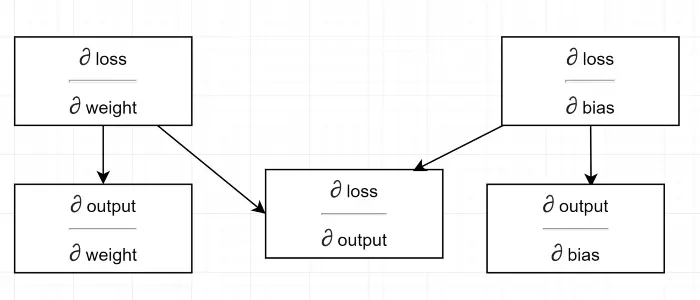
Ver todos os cálculos dependem do gradiente de saída (∂ perda/∂ saída) . É por isso que estamos calculando primeiro no backpass (Linha # 34-36).

Na verdade, em frameworks de ML de alto nível, por exemplo no PyTorch, você não precisa escrever códigos para backpass! Durante a passagem para frente, ele cria gráficos computacionais e, durante a passagem para trás, percorre a direção oposta no gráfico e calcula gradientes usando a regra da cadeia.

∂ perda / ∂ saída

Definimos essa variável por grad_output no código, que calculamos na Linha#34–36. Vamos descobrir a razão por trás da fórmula que usamos no código.

Lembre-se, estamos alimentando todos os 100 celsius_values ​​na máquina juntos. Assim, grad_output será um array de 100 elementos, cada elemento contendo gradiente de saída para o elemento correspondente em celsius_values ​​. Para simplificar, vamos considerar que existem apenas 2 itens em celsius_values ​​.

Então, quebrando a linha #30,

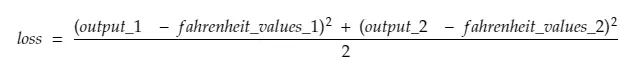
Onde,

output_1 = valor de saída para o 1º valor celsius

output_2 = valor de saída para o 2º valor celsius

fahreinheit_values_1 = Valor real de fahreinheit para o 1º valor celsius

fahreinheit_values_1 = Valor real de fahreinheit para o 2º valor celsius

Agora, a variável resultante grad_output conterá 2 valores — gradiente de output_1 e output_2, significando:

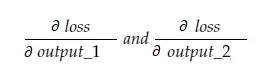
Vamos calcular apenas o gradiente de output_1, e então podemos aplicar a mesma regra para os outros.

Hora do cálculo!

Que é o mesmo que a linha # 34-36.

Gradiente de peso

Imagine, temos apenas um elemento em celsius_values. Agora:

Que é o mesmo que a Linha #38–40. Para 100 celsius_values, os valores de gradiente para cada um dos valores serão somados. Uma pergunta óbvia seria por que não estamos reduzindo o resultado (ou seja, dividindo por SAMPLE_SIZE). Como estamos multiplicando todos os gradientes com um fator pequeno antes de atualizar os parâmetros, não é necessário (veja a última seção Atualizando Parâmetros).

Gradiente de viés

Qual é o mesmo que a Linha # 42. Assim como os gradientes de peso, esses valores para cada uma das 100 entradas estão sendo somados. Novamente, tudo bem, pois os gradientes são multiplicados com um pequeno fator antes de atualizar os parâmetros.

Atualizando parâmetros

Finalmente, estamos atualizando os parâmetros. Observe que os gradientes multiplicados por um pequeno fator (LEARNING_RATE) antes de serem subtraídos, para tornar o treinamento estável. Um valor grande de LEARNING_RATE causará um problema de overshooting e um valor extremamente pequeno tornará o treinamento mais lento, o que pode precisar de muito mais iterações. Devemos encontrar um valor ideal para ele com algumas tentativas e erros. Existem muitos recursos on-line, incluindo este para saber mais sobre a taxa de aprendizagem.

Observe que a quantidade exata que ajustamos não é extremamente crítica. Por exemplo, se você ajustar LEARNING_RATE um pouco, as variáveis ​​descent_grad_weight e descent_grad_bias (Linha#49–50) serão alteradas, mas a máquina ainda poderá funcionar. O importante é garantir que esses valores sejam derivados diminuindo os gradientes com o mesmo fator (LEARNING_RATE neste caso). Em outras palavras, “manter a descida dos gradientes proporcional” importa mais do que “quanto eles descem ”.

Observe também que esses valores de gradiente são, na verdade, a soma dos gradientes avaliados para cada uma das 100 entradas. Mas como eles são dimensionados com o mesmo valor, tudo bem, conforme mencionado acima.

Para atualizar os parâmetros, temos que declará-los com a palavra-chave global (na Linha#47).

Para onde ir a partir daqui

O código seria muito menor substituindo os loops for pela compreensão da lista de maneira pythonic. Dê uma olhada agora - não levaria mais do que alguns minutos para entender.

Se você entendeu tudo até agora, provavelmente é um bom momento para ver as partes internas de uma rede simples com vários neurônios/camadas — aqui está um artigo.