Sinta o cálculo com seu senso de programação

Acredito que as pessoas que podem codificar têm a capacidade de entender conceitos mais complicados do que cálculo. Uma razão pela qual existem muitos programadores talentosos por aí que ainda estão lutando com o cálculo não é que seja difícil. É principalmente porque fomos ensinados de maneira errada (junto com muitos outros tópicos).

Se você já fez alguma codificação em sua vida – até mesmo alguns exercícios de brinquedo, como gerar números primos, você já deve ter feito coisas semelhantes que acontecem no cálculo, mas nunca teve a chance de se relacionar.

O objetivo desta escrita não é ensinar cálculo nem programação – mas ajudá-lo a conectar alguns pontos.

Vou chegar à parte de codificação em um minuto. Mas permita-me dar um breve histórico antes disso.

Taxa de variação

O cálculo diferencial fala sobre a “taxa de variação”. Vamos tentar entender o que isso significa.

Para uma mudança em uma variável (x), a taxa de mudança de uma função é simplesmente a mudança na função dividida pela mudança em x. Vamos visualizar com números reais:

Considere 2 pontos x=2 e x=6, e uma função y=f(x) = x².

Além disso, considere dx = distância entre esses 2 pontos no eixo x. E dy é a distância entre os valores de y para esses valores de x.

Então, a taxa de variação em y de x=2 para x=6 é

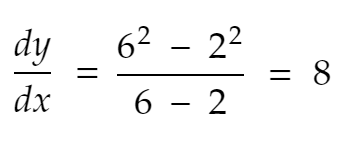
Derivado

Agora — a derivada dy/dx é a taxa de variação em y para uma variação infinitesimalmente pequena em x. Como essa distância (6–2=4) não é infinitesimalmente pequena — nem perto, não podemos chamar a equação acima de derivada. Então, vamos escolher um número menor, 0,1, por enquanto.

Quando x = 0, y = x² = 0² = 0.

Vizinho mais próximo da direção positiva, x = 0,1. Aí y torna-se 0,1² = 0,01.

Então,

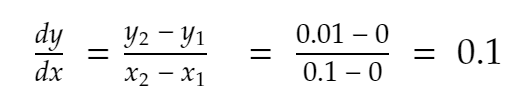
Vamos tentar mais uma vez. Vizinho mais próximo de 0,1 para a direção positiva, x = 0,2. Então, y se torna 0,2² = 0,04. Então,

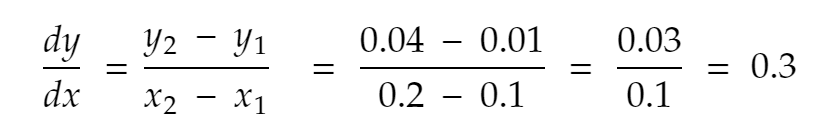
Se repetirmos o processo mais algumas vezes, é isso que obtemos:

Aqui está o arquivo excel se você quiser brincar com ele.

dx (que é nossa distância fictícia infinitesimalmente pequena entre 2 pontos adjacentes no eixo x) é 0,1 em nosso contexto.

x está aumentando de acordo.

y é simplesmente x².

dy é a distância entre 2 valores de y adjacentes. Por exemplo, quando x= 0,1, a distância entre o atual y (0,01) e o próximo y (0,04) é 0,03 — então, dy é 0,03 em x=0,1.

dy/dx é dy dividido por dx.

dy/dx / x é dy/dx dividido por x.

Agora observe que, à medida que x aumenta, a última linha se aproxima de 2, o que significa — a taxa de variação de x² em relação a x se aproxima do dobro de x, que é 2x .

Lembre-se da derivada de x² em relação a x? 2x! Encontrando alguma conexão?

Tempo de codificação

Vamos tentar as coisas no código que discutimos até agora.

Supondo que você já tenha o Python instalado, no terminal, execute:

Depois disso, execute o seguinte código Python:

Aqui:

x : contendo números de 0 a 9.

y : outro array, cada elemento é quadrado do elemento x correspondente

dy : Outro array inicializado com zeros. Vamos colocar distâncias y nesta matriz.

dydx : Outro array inicializado com zeros. Ele conterá o valor dy/dx de cada ponto.

dx : Bem óbvio - é o tamanho do passo. Distância entre 2 números consecutivos, que diminui à medida que SIZE aumenta. Se SIZE = 10, dx = 1. Se SIZE = 100, dx = 0,1.

Primeiro, estamos derivando dy para cada ponto. Então calculamos dydx a partir dele.

Notar que:

Aqui estamos omitindo o primeiro e o último valores. O primeiro valor de x é 0, o que produzirá um erro de divisão zero. E não podemos calcular o último valor de dy/dx, pois não temos o último valor de dy — porque exigiria próximo ao último valor disponível de y, que não temos aqui.

Se tudo correr bem, você obterá este gráfico:

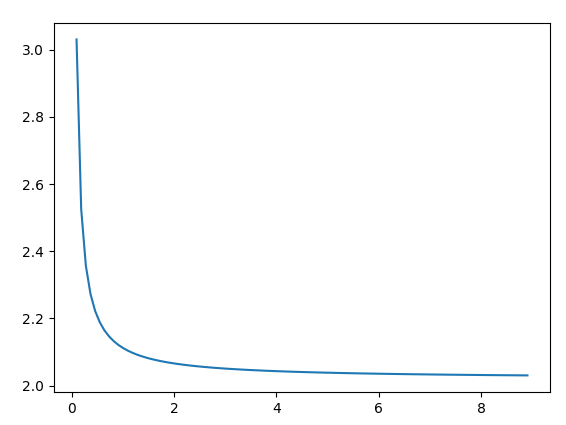
O que você entende do enredo

Como você pode ver, o gráfico está se aproximando de 2. Aumente o valor de SIZE (significando configuração inferior a dx) e veja como o gráfico se aproxima mais rapidamente de 2.

Segunda Derivada

Agora que você chegou até aqui, apenas mais alguns passos para realizar a segunda derivada, que lhe dará a intuição para derivada de qualquer ordem.

Como você se lembra, a segunda derivada é a taxa de variação da primeira derivada em relação a x. Simplificando - dy/dx na segunda derivada é como y na primeira derivada.

Vamos fazer as seguintes modificações no código acima:

Declare mais 2 arrays:

d2ydx2 : Que representará a segunda derivada:

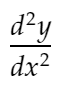
distance_dydx: Para representar a distância entre o valor dy/dx entre 2 pontos adjacentes

Aqui está o código completo para a segunda derivada:

Depois de calcular dydx no loop for, executamos outro loop para calcular a segunda derivada. Com alguma codificação sábia, poderíamos calcular a segunda derivada no mesmo loop (tente como exercício) — mas eu as mantive separadas aqui para maior clareza.

Observe também que:

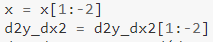
Como fizemos na primeira derivada, estamos omitindo alguns valores aqui também. Os últimos 2 valores são omitidos, pois o segundo do último exigiria o último valor da “primeira derivada”, que não pudemos calcular (já que não tínhamos o valor y necessário para ele — conforme descrito acima). Isso significa que temos que omitir os 3 últimos valores no caso da 3ª derivada?🤔 — isso é para você encontrar.

Aqui está o gráfico de saída:

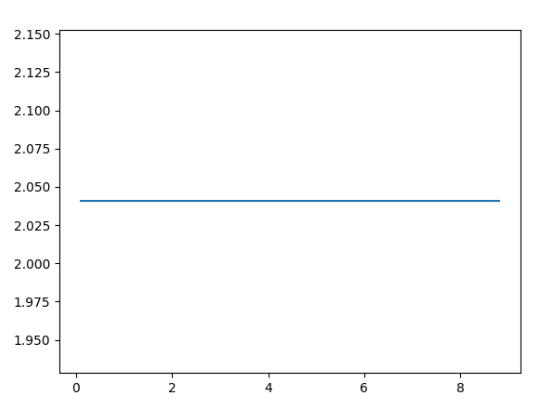
O que vemos aqui?

Como você sabe desde o ensino médio:

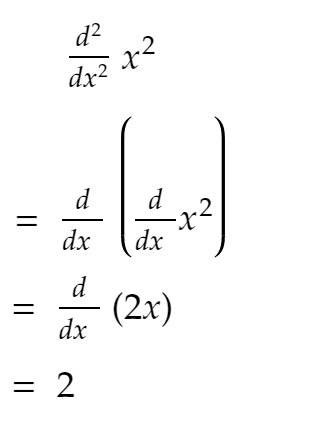
Agora, como você vê no código acima, a segunda derivada permanece praticamente constante, e se você continuar aumentando SIZE - ela se aproxima de 2!

Por que a taxa de mudança é importante

Você pode estar se perguntando:

— Por que passamos por todos esses problemas desagradáveis? Que informações úteis obtemos da taxa de variação ou derivada?

— Por que não podemos simplesmente seguir a taxa de variação para qualquer quantia? Por que apenas infinitesimalmente pequeno? Que informações obtemos da taxa de variação em relação a valores infinitesimalmente pequenos , que não podem ser encontrados na taxa de variação em relação a valores maiores?

— Essa coisa infinitesimalmente pequena parece um hack? Nós trabalhamos com alguns números pequenos acima, mas certamente não são infinitesimalmente pequenos.

Se eu me permitisse continuar, você iria embora vendo a extensão deste artigo e não teria chegado tão longe. Talvez abordemos essas questões outro dia 😀.