Estatísticas Bayesianas: um primer rápido e sem exageros para um testador A/B
Publicados: 2022-06-23
Quão confiante você está em sua capacidade de interpretar os resultados fornecidos por sua ferramenta de teste A/B?
Digamos que você esteja usando uma ferramenta construída com base nas estatísticas Bayesianas e ela lhe disse que “B” tem 70% de chance de vencer “A”, então “B” é o vencedor. Você sabe o que isso significa e como deve informar sua estratégia de CRO?
Neste artigo, você aprenderá os fundamentos das estatísticas Bayesianas que o ajudarão a retomar o controle de seus testes A/B, incluindo
- Uma visão imparcial das estatísticas Bayesianas
- Vantagens e desvantagens do freqüentista vs bayesiano
- A preparação que você precisa para interpretar e usar com confiança os resultados do teste A/B Bayesiano, evitando algumas armadilhas de mitos comuns.
- O que é Estatística Bayesiana?
- A História da Origem Bayesiana
- Um Exemplo de Estatística Bayesiana Aplicada a Testes A/B
- Um breve glossário de termos bayesianos que importam para testadores A/B
- Inferência Bayesiana
- Probabilidade Condicional
- Distribuição de Probabilidade/Distribuição de Probabilidade
- Distribuição de Crenças Prévias
- Conjugação
- Conjugados Anteriores
- Função de perda
- O que é Estatística Frequentista?
- Teste A/B Bayesiano vs Frequentista
- O Quadro Frequentista
- A Estrutura Bayesiana
- O que as estatísticas bayesianas realmente dizem a você em testes A/B?
- Probabilidade de ser o melhor (P2BB)
- Elevação esperada
- Perda esperada
- Mitos em torno das estatísticas bayesianas a serem evitados
- Mito 1: Bayesianos declaram suas suposições, frequentistas não
- Mito #2. Os métodos bayesianos oferecem as respostas que você realmente deseja
- Mito 3: A inferência bayesiana ajuda você a comunicar a incerteza melhor do que a inferência frequente
- Mito #4. Os resultados do teste A/B Bayesiano são imunes à espionagem
- Mito #5. Estatísticas freqüentes são ineficientes, pois você deve esperar por um tamanho de amostra fixo
- Então, você deve escolher Bayesiano ou Frequentista? Há um lugar para ambos.
- Dica importante
Preparar? Vamos começar com o básico.
O que é Estatística Bayesiana?
A estatística Bayesiana é uma abordagem de análise estatística baseada no teorema de Bayes, que atualiza as crenças sobre eventos à medida que novos dados ou evidências sobre esses eventos são coletados. Aqui, a probabilidade é uma medida de crença de que um evento ocorre.
O que isso significa: Se você tiver uma crença anterior sobre um evento e obter mais informações relacionadas a ele, essa crença mudará (ou pelo menos será ajustada) para uma crença posterior .
Isso é útil para entender a incerteza ou ao trabalhar com muitos dados ruidosos, como na otimização da taxa de conversão para comércio eletrônico e no aprendizado de máquina.
Vamos imaginar isso:
Digamos, por exemplo, que você está assistindo a uma corrida de carrinho de supermercado da faculdade e, em seguida, um espectador animado desafia você a apostar que o cara de camiseta vermelha carregando a senhora de camiseta verde vencerá. Você pensa sobre isso e responde que o cara de jaqueta preta e a garota de capuz preto ganharão.

Outro espectador por cima e sussurrou uma dica para você: “O cara da camiseta vermelha venceu as últimas 3 corridas de 4”. O que acontece com sua aposta? Você não tem mais certeza, certo?
Supondo que você também saiba que a última vez que o cara da jaqueta preta usou seus óculos de sol da sorte, ele ganhou. E as vezes que ele não usava, o cara da camiseta vermelha ganhava.
Hoje, você vê que o cara da jaqueta preta está usando esses óculos. Sua crença muda novamente. Agora você tem mais fé em sua aposta, correto? Nesta história, você atualizou sua crença toda vez que obteve evidências de novos dados. Essa é a abordagem Bayesiana.
A História da Origem Bayesiana
Quando o reverendo Thomas Bayes pensou pela primeira vez em sua teoria, ele não achou que fosse digna de publicação. Assim, permaneceu em suas notas por mais de uma década. Foi quando sua família pediu a Richard Price para examinar suas notas que Price descobriu as notas que formavam a base do Teorema de Bayes.
Tudo começou com um experimento mental para Bayes. Ele pensou em sentar de costas para uma mesa perfeitamente plana e quadrada e ter um assistente jogando uma bola sobre a mesa.
A bola poderia cair em qualquer lugar da mesa, mas Bayes achou que poderia adivinhar onde atualizando seus palpites com novas informações. Quando a bola pousava na mesa, ele fazia com que o assistente lhe dissesse se ela pousava à esquerda ou à direita, na frente ou atrás de onde a bola anterior havia pousado.
Ele notou isso e escutou enquanto mais bolas pousavam na mesa. Com informações adicionais como essa, ele descobriu que poderia melhorar a precisão de seus palpites a cada lance. Isso trouxe a ideia de atualizar nosso entendimento à medida que adquirimos mais evidências da observação.
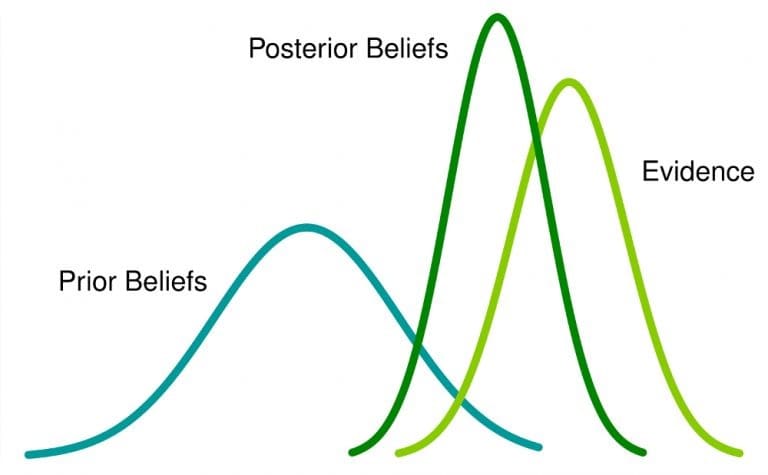
A abordagem bayesiana à análise de dados é aplicada em vários campos, como ciência e engenharia, e inclui até esportes e direito.
Em experimentos controlados randomizados online, especificamente testes A/B, você pode usar a abordagem Bayesiana em 4 etapas:
- Identifique sua distribuição anterior.
- Escolha um modelo estatístico que reflita suas crenças.
- Execute o experimento.
- Após a observação, atualize suas crenças e calcule uma distribuição posterior.
Você atualiza suas crenças usando um conjunto de regras chamado algoritmo Bayesiano.
Um Exemplo de Estatística Bayesiana Aplicada a Testes A/B
Vamos ilustrar um exemplo de teste A/B Bayesiano.
Imagine que executamos um teste A/B simples no botão CTA de uma loja da Shopify. Para “A”, usamos “Adicionar ao carrinho” e para “B”, usamos “Adicionar ao seu carrinho”.
Veja como um frequentista abordará o teste.
Existem dois mundos alternativos: Um onde A e B não são diferentes, então o teste não mostrará nenhuma diferença na taxa de conversão. Essa é a hipótese nula. E no outro mundo, há uma diferença, então um botão terá um desempenho melhor que o outro.
O frequentista assumirá que vivemos no mundo 1 onde não há diferença nos botões de CTA, ou seja, assumindo que a hipótese nula é verdadeira. E então eles tentarão provar que isso está errado com um nível de certeza pré-determinado chamado nível de significância.
Mas é assim que um Bayesiano abordará o mesmo teste:
Eles começam com uma crença prévia de que ambos os botões A e B têm chances iguais de produzir uma taxa de conversão entre 0 e 100%. Portanto, há igualdade de botões desde o início - ambos têm 50% de chance de ter o melhor desempenho.
Em seguida, o teste começa e os dados são coletados. A partir da observação de novas informações, os testadores A/B Bayesianos atualizarão seus conhecimentos. Então, se B está se mostrando promissor, eles podem chegar a uma crença posterior com base nessa observação dizendo: “B tem 61% de chance de vencer A”.
Existem diferenças fundamentais entre os dois métodos.
É por isso que é importante mantermos uma abordagem imparcial aos testes A/B Bayesianos.
A maioria das ferramentas de teste A/B Bayesianas – talvez para fins de marketing – adota uma postura antifrequencial extrema e defende o argumento de que Bayesian é melhor em dizer qual variante é mais “lucrativa”.
Mas alguma abordagem estatística única para testes A/B possui os direitos exclusivos de insights?
Se levarmos mais longe o argumento bayesiano, podemos nos deparar com estudos em que os entrevistados dizem que querem saber qual é o melhor curso de ação ou que desejam maximizar os lucros ou algo semelhante. Isso coloca a questão firmemente no território da teoria da decisão – algo em que nem a inferência bayesiana nem a inferência frequentista podem ter uma palavra direta.
Georgi Georgiev, criador do Analytics-toolkit.com e autor de “Statistical Methods in Online A/B Testing”
Daremos um breve mergulho nesses detalhes nas seções a seguir. Por enquanto, vamos tornar o resto desta cartilha fácil de entender.
Um breve glossário de termos bayesianos que importam para testadores A/B
Inferência Bayesiana
A inferência bayesiana está atualizando a probabilidade de uma hipótese com novos dados. É construído em torno de crenças e probabilidades.
A inferência bayesiana aproveita a probabilidade condicional para nos ajudar a entender como os dados afetam nossas crenças. Digamos que começamos com uma crença prévia de que o céu é vermelho. Depois de analisar alguns dados, logo perceberíamos que essa crença anterior está errada. Assim, realizamos uma atualização bayesiana para melhorar nosso modelo incorreto sobre a cor do céu, terminando com uma crença posterior mais acurada .
Michael Berk em Rumo à Ciência de Dados
Probabilidade Condicional
A probabilidade condicional é a probabilidade de um evento dado que outro evento ocorreu. Ou seja, a probabilidade de A sob a condição B.
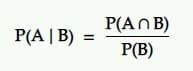
Tradução: A probabilidade de um evento A acontecer dado outro evento B é igual à probabilidade de B e A acontecerem juntos dividida pela probabilidade do evento B.
Distribuição de Probabilidade/Distribuição de Probabilidade
As distribuições de probabilidade são distribuições que mostram a probabilidade de seus dados assumirem um valor específico.
Onde seus dados podem assumir vários valores, por exemplo, uma categoria como cores que podem ser cinza, vermelho, laranja, azul, etc., sua distribuição é multinomial. Para um conjunto de números, a distribuição pode ser normal. E para valores de dados que poderiam ser sim/não ou verdadeiro/falso, seria binomial.
Distribuição de Crenças Prévias
Ou distribuição de probabilidade a priori, simplesmente chamada a priori, expressa sua crença antes de você obter evidências de novos dados. Portanto, é uma expressão de sua crença inicial que você atualizará depois de considerar algumas evidências usando análise Bayesiana (ou inferência).
Conjugação
Em primeiro lugar, conjugado refere-se a ser unido, geralmente em pares. Na teoria da probabilidade Bayesiana, a conjugação é assumir que o anterior é conjugado com a probabilidade.
Se o posterior tem a mesma forma funcional do anterior, então o anterior é conjugado com a função de verossimilhança. Isso mostra como a função de verossimilhança atualiza a distribuição anterior.
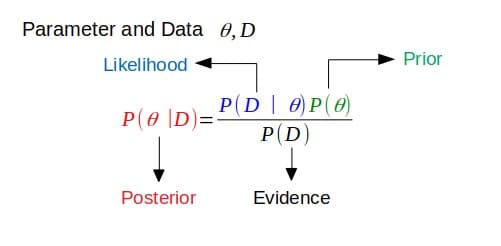
Conjugados Anteriores
Isso está ligado à definição acima. Se o posterior estiver na mesma família de distribuição de probabilidade (ou tiver a mesma forma funcional) que a distribuição de probabilidade anterior, então o anterior e o posterior são distribuições conjugadas. Neste caso, o prior é chamado de prior conjugado para a função de verossimilhança.
Eles podem ser subjetivos (com base no conhecimento do experimentador), objetivos e informativos (com base em dados históricos) ou não informativos.
Função de perda
Uma função de perda é uma maneira de quantificar a perda medindo o quão ruim é nossa estimativa atual. Isso nos ajuda a minimizar a perda de testes de hipóteses, especialmente ao expressar uma inferência que se encontra em uma faixa de valores prováveis, e apoiar a tomada de decisões com os resultados de nossos testes.
Agora que está fora do caminho, podemos seguir em frente.
Se você está no quarteirão há algum tempo, provavelmente já se deparou com mais do que alguns memes de estatísticas Frequentistas vs Bayesianos.

Ambos os lados parecem buscar respostas de direções opostas, mas será que realmente é esse o caso? Para entender isso melhor (mantendo-se imparcial), vamos visitar o acampamento de Frequentistas.
O que é Estatística Frequentista?
Esta é a primeira técnica inferencial que a maioria das pessoas aprende em estatística. As estatísticas freqüentistas calculam a probabilidade de um evento (hipótese) ocorrer com frequência nas mesmas condições.
O teste de hipóteses A/B usando a abordagem frequentista segue estas etapas:
- Declare algumas hipóteses. Normalmente, a hipótese nula é que a nova variante “B” não é melhor que a original “A”, enquanto a hipótese alternativa declara o contrário.
- Determine um tamanho de amostra com antecedência usando um cálculo de poder estatístico , a menos que você esteja usando abordagens de teste sequenciais. Use uma calculadora de tamanho de amostra que considere o poder estatístico, a taxa de conversão atual e o efeito mínimo detectável.
- Execute o teste e espere que cada variação seja exposta ao tamanho de amostra pré-determinado.
- Calcule a probabilidade de observar um resultado pelo menos tão extremo quanto os dados sob a hipótese nula (p-valor). Rejeite a hipótese nula e implante a nova variante em produção se o valor p < 5%.
Como isso se compara ao Bayesiano? Vamos ver…
Teste A/B Bayesiano vs Frequentista
Este é um debate notório em qualquer lugar onde a inferência estatística é usada. E para ser franco, é inútil. Ambos têm seus méritos e casos em que são o melhor método a ser usado.
Ao contrário do que a maioria dos promotores em ambos os campos vai fazer você pensar, eles são semelhantes em vários aspectos e nenhum se aproxima da verdade do que o outro - embora suas abordagens sejam diferentes.
Quando aplicado ao teste A/B, por exemplo, nenhum método específico lhe dará uma previsão absoluta e precisa em termos do curso de ação que causará o crescimento do negócio. Em vez disso, o teste A/B ajuda a remover o risco da tomada de decisões.
Não importa como você analisa seus dados – usando abordagens Bayesianas ou Frequentistas – você pode fazer movimentos com algum nível de certeza de que está certo.
E por essa razão, ambos os modelos estatísticos são válidos. Bayesian pode ter uma vantagem de velocidade, mas é mais computacionalmente exigente do que o Frequentist.
Confira outras diferenças...
O Quadro Frequentista
A maioria de nós está familiarizada com a abordagem frequentista dos cursos introdutórios de estatística. Definimos a metodologia acima — desde declarar a hipótese nula, determinar o tamanho da amostra, coletar dados por meio de um experimento aleatório e, finalmente, observar um resultado estatisticamente significativo.
No Frequentismo, vemos a probabilidade como fundamentalmente relacionada às frequências de eventos repetidos. Então, em um sorteio justo, um Frequentista acredita que, se adivinhar com frequência suficiente, obterá cara 50% das vezes e o mesmo para coroa.
Mentalidade frequente: “Se eu repetir o experimento nas mesmas condições repetidamente, quais são as chances de meu método obter a resposta certa?”
A Estrutura Bayesiana
Enquanto a abordagem frequentista trata o parâmetro populacional para cada variante como uma constante (desconhecida), a abordagem bayesiana modela cada valor de parâmetro como uma variável aleatória com alguma distribuição de probabilidade.
Aqui, você calcula distribuições de probabilidade (e, portanto, valores esperados) para os parâmetros de interesse diretamente.
E para modelar a distribuição de probabilidade para cada variante, contamos com a regra de Bayes para combinar os resultados do experimento com qualquer conhecimento prévio que tenhamos sobre a métrica de interesse. Podemos simplificar os cálculos usando uma priori conjugada.
Alex Birkett resumiu o algoritmo Bayesiano desta forma:
- Defina a distribuição prévia que incorpora suas crenças subjetivas sobre um parâmetro. O anterior pode ser não informativo ou informativo.
- Reúna dados.
- Atualize sua distribuição a priori com os dados usando o teorema de Bayes (embora você possa ter métodos Bayesianos sem o uso explícito da regra de Bayes — veja Bayesiano não paramétrico) para obter uma distribuição posterior. A distribuição posterior é uma distribuição de probabilidade que representa suas crenças atualizadas sobre o parâmetro após ter visto os dados.
- Analise a distribuição posterior e resuma-a (média, mediana, dp, quantis…).
Em suma, o experimentador bayesiano se concentra em sua própria perspectiva e no que probabilidade significa para ele. A opinião deles evolui com os dados observados. Os frequentadores, por outro lado, acreditam que a resposta certa está por aí em algum lugar.

Entenda que o debate Frequentista vs Bayesiano não afeta tanto a análise de testes A/B pós. As principais diferenças entre os dois campos estão mais relacionadas ao que pode ser testado.
As estatísticas de probabilidade geralmente não são muito usadas em análises subsequentes. O argumento Bayesiano-Frequentista é mais aplicável em relação à escolha das variáveis a serem testadas no paradigma A/B, mas mesmo assim a maioria dos testadores A/B violam as hipóteses de pesquisa, probabilidade e intervalos de confiança .
Dr. Rob Balon para CXL
Georgi detalha ainda:
Existem várias calculadoras Bayesianas on-line e pelo menos um grande fornecedor de software de teste A/B aplicando um mecanismo estatístico Bayesiano que usam os chamados priors não informativos (um pouco incorreto, mas não vamos nos aprofundar nisso). Na maioria dos casos, os resultados dessas ferramentas coincidem numericamente com os resultados de um teste frequentista nos mesmos dados. Digamos que a ferramenta Bayesiana relatará algo como '96% de probabilidade de que B seja melhor que A', enquanto a ferramenta frequentista produzirá um valor p de 0,04, que corresponde a um nível de confiança de 96%.
Em uma situação como a acima, que é muito mais comum do que alguns gostariam de admitir, ambos os métodos levarão à mesma inferência e o nível de incerteza será o mesmo, mesmo que a interpretação seja diferente.
O que um Bayesiano diria sobre esse resultado? Ele transforma o valor-p em uma probabilidade posterior adequada ao visualizar um cenário no qual não há informação prévia? Ou todas essas aplicações de testes Bayesianos são equivocadas por usar uma priori não informativa per se?
Realmente não há necessidade de escolher um acampamento e encontrar um local atrás de cobertura para atirar pedras no outro acampamento. Há até evidências de que ambas as estruturas produzem os mesmos resultados. Não importa a estrada que você escolher, o destino provavelmente será o mesmo. Depende de como você pode chegar lá com o Frequentist vs Bayesian.
Por exemplo:
- Há dados que mostram que o teste bayesiano é mais rápido e a escolha preferida para experimentos interativos:
Como o paradigma Bayesiano permite que os experimentadores quantifiquem formalmente a crença e incorporem conhecimento adicional, é mais rápido do que a análise estatística tradicional.
Em uma simulação de teste Bayesiano A/B, quando o critério de decisão foi ajustado (ou seja, aumentando a tolerância a erros), 75% dos experimentos concluíram dentro de 22,7% das observações exigidas pela abordagem tradicional (a um nível de significância de 5%). E registrou apenas 10% de erro tipo II. - O Bayesiano também é considerado mais tolerante, enquanto o Frequentista é avesso ao risco:
Enquanto muitos testes Frequentistas usam uma significância estatística de 95%, os Bayesianos podem ficar satisfeitos com menos do que isso. Se uma variante tiver 78% de chance de vencer o controle, dependendo da perda esperada, pode ser uma boa decisão implantar essa variante.
Se você estiver errado e a perda esperada for inferior a um por cento, isso é um dano bastante insignificante para muitas empresas. Essa abordagem desconexa pode ser mais adequada para tomada de decisões rápidas em cenários de risco muito baixo. - No entanto, as simulações e cálculos bayesianos são pesados de computação:
Frequentista, por outro lado, é baseado em papel e caneta. Advertência: Se sua ferramenta de teste A/B usa Bayesian e você não sabe quais suposições estão sendo adicionadas aos seus dados, não pode confiar na “resposta” que seu fornecedor lhe dá. Leve com uma pitada de sal. E execute sua própria análise.
Nem tudo é sol e arco-íris com Bayesian. Como Georgi aponta com esta lista de perguntas:
- “Você quer obter o produto da probabilidade anterior e a função de verossimilhança?”
- “Você quer a mistura de probabilidades anteriores e dados como saída?”
- “Você quer crenças subjetivas misturadas com os dados para produzir a saída?” (se estiver usando informações anteriores)
- “Você se sentiria confortável em apresentar estatísticas nas quais há informações prévias consideradas altamente certas misturadas com os dados reais?”
Todos esses são aspectos das estatísticas bayesianas, em termos leigos.
O que as estatísticas bayesianas realmente dizem a você em testes A/B?
Você projetou seu teste A/B para fornecer insights sobre como uma alteração afeta sua métrica de interesse, como a taxa de conversão ou a receita por visitante.
Quando você usa uma ferramenta que funciona com estatísticas Bayesianas, é importante entender o que seus resultados significam porque “B é o vencedor” não significa exatamente o que a maioria das pessoas pensa que significa.
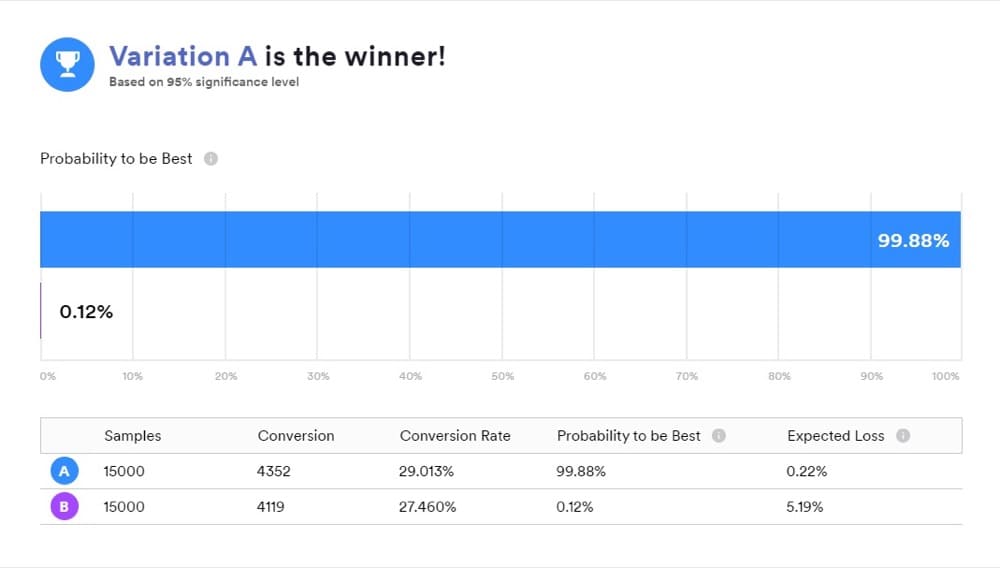
É uma maneira conveniente de apresentar resultados, mas não foi isso que seu teste revelou. Em vez disso, as respostas que você deseja estão em comparações posteriores de “A” e “B”.
Aqui estão os 3 métodos de comparação:
Probabilidade de ser o melhor (P2BB)
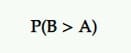
Esta é a probabilidade que declara um vencedor no teste Bayesiano A/B.
A variante com a probabilidade de ser a melhor é aquela com a maior probabilidade de continuar superando a outra.
Isso é calculado a partir de um conjunto de amostras posteriores da medida de interesse do original e do desafiante.
Então, se B tem a maior probabilidade de aumentar suas taxas de conversão, por exemplo, B é declarado vencedor.
Elevação esperada
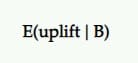
Então, se B é o vencedor, quanta elevação devemos esperar dele? Continuaria a entregar os mesmos resultados que vimos no teste?
Esse é o insight esperado que a elevação procura fornecer. O aumento esperado de escolher B sobre A, dado um conjunto de amostras posteriores, é definido como o intervalo de credibilidade (ou média) do aumento percentual.
Em testes A/B, geralmente comparamos isso como o desafiante com o controle. Assim, se o desafiante perdeu, é representado em valores negativos (como -11,35%) e valores positivos (como +9,58%) se ganhou.
Perda esperada
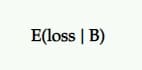
Como não há 100% de probabilidade de que B seja melhor que A, há uma chance de registrar uma perda se você escolher B em vez de A. Isso é representado como perda esperada e, assim como no aumento esperado, é expresso a partir do ponto de vista do desafiante contra o controle.
Ele informa o risco de escolher sua variante P2BB (ou seja, o vencedor declarado).
Antes de mergulharmos nos mitos, um enorme obrigado à lenda da análise Georgi Georgiev. Suas análises aprofundadas de inferência freqüentista vs Bayesiana e probabilidade e estatísticas Bayesianas em testes A/B inspiraram a próxima seção.
Mitos em torno das estatísticas bayesianas a serem evitados
Com uma rivalidade quase tão antiga quanto desnecessária, o debate Bayesiano vs Frequentista reuniu muitas informações – e deu origem a muitos mitos.
O maior desses mitos (mito nº 2) é promovido por fornecedores de ferramentas de teste A/B para dizer por que uma abordagem é melhor que a outra.
Mas depois de ler as seções acima, você sabe melhor.
Vamos revelar os buracos nesses mitos.
Mito 1: Bayesianos declaram suas suposições, frequentistas não
Isso sugere que os Bayesianos fazem suposições na forma de distribuições anteriores e estas estão abertas para avaliação. Mas os Frequentistas fazem suposições que estão escondidas no meio da matemática.
Por que está errado: Bayesianos e Frequentistas fazem suposições subjacentes semelhantes, a única diferença é que Bayesianos fazem suposições adicionais - além da matemática.
Modelos freqüentes usam suposições na matemática, como a forma da distribuição, homogeneidade ou heterogeneidade do efeito entre as observações e a independência da observação. E eles não estão escondidos. Na verdade, eles são amplamente discutidos na comunidade estatística e declarados para todos os testes estatísticos frequentistas.
A verdade: os frequentistas declaram explicitamente suas suposições e dão um passo adiante para testar as suposições: testes de normalidade, teste de ajuste (sob o qual temos o teste de incompatibilidade da razão amostral) e muito mais.
Mito #2. Os métodos bayesianos oferecem as respostas que você realmente deseja
O equívoco aqui é que os valores de p e os intervalos de confiança não dizem aos testadores o que eles querem saber, enquanto as probabilidades posteriores e os intervalos confiáveis sim. As pessoas querem saber coisas como
- A probabilidade de que B supere A e
- A probabilidade de que o resultado não seja uma coincidência.
Valores-P e testes de hipóteses (inferência direta) não fornecem essa informação, mas a inferência inversa sim.
Por que está errado: Esta é uma questão de linguística. Geralmente, quando não estatísticos usam termos como “probabilidade”, “acaso” e “probabilidade”, eles não os estão usando com seu significado técnico em mente. Pesquise mais fundo e você descobrirá que eles estão tão confusos sobre inferência inversa quanto sobre inferência direta.
De acordo com Georgi Georgiev, perguntas como estas começam a surgir:
- “ O que é uma probabilidade anterior? Que valor traz?”
- “O que é uma função de verossimilhança?”
- “Que probabilidade 'anterior', não tenho dados anteriores?”
- “Como defendo a escolha de uma probabilidade anterior?”
- “Existe uma maneira de comunicar exatamente o que os dados dizem, sem nenhuma dessas misturas?”
A verdade: deve haver uma visão melhor sobre o que os testadores querem saber, não sobre sua má interpretação de termos técnicos. Valores-P, intervalos de confiança e outros informam o quão bem sondados são os resultados com os dados coletados. Eles forneceram uma medida de certeza sem a influência de suposições prévias subjetivas e não testadas.
Mito 3: A inferência bayesiana ajuda você a comunicar a incerteza melhor do que a inferência frequente
Porque os resultados dos testes produzem insights mais “significativos”.
Por que está errado: As abordagens Frequentista e Bayesiana têm ferramentas semelhantes para ajudá-lo a comunicar a certeza e os resultados do seu teste A/B.
| Frequentista | Bayesiano | ||||||||||
| ● Estimativas de pontos | ● Estimativas de pontos | ||||||||||
| ● Valores P | ● Intervalos confiáveis | ||||||||||
| ● Intervalos de confiança | ● Fatores de Bayes | ||||||||||
| ● Curvas de valor P | ● Distribuições posteriores (realizar a mesma tarefa como as curvas freqüentistas) | ||||||||||
| ● Curvas de confiança | |||||||||||
| ● Curvas de gravidade, etc. |
A verdade: tudo depende de como você os usa. Ambos os métodos são igualmente eficazes na comunicação de incerteza. No entanto, existem diferenças em como eles apresentam a medida de incerteza.
Mito #4. Os resultados do teste A/B Bayesiano são imunes à espionagem
Alguns estatísticos bayesianos argumentam que você pode interromper um teste bayesiano quando vir um “vencedor claro” e isso faz pouca diferença no resultado final.
Você provavelmente sabe que isso é inaceitável em testes Frequentistas, então é considerado uma desvantagem quando comparado ao Bayesiano. Mas é mesmo?
Por que está errado: Em um estudo de 1969 no Journal of the Royal Statistical Society intitulado “Repeated Significance Tests on Accumulating Data”, Armitage et al. mostrou como a parada opcional baseada em resultados aumenta a probabilidade de erro.
Você não pode simplesmente parar quando perceber um vencedor, atualizar seu posterior e usá-lo como seu próximo prior sem ajustar o modo como a análise Bayesiana funciona.
A verdade: Espreitar afeta a inferência Bayesiana tanto quanto o Frequentista (se você quiser fazer certo).
Mito #5. Estatísticas freqüentes são ineficientes, pois você deve esperar por um tamanho de amostra fixo
Alguns membros da comunidade CRO acreditam que os testes estatísticos frequentistas devem ser executados com um tamanho de amostra fixo e predeterminado, caso contrário os resultados são inválidos.
Como resultado, você espera mais do que o necessário para obter os resultados desejados.
Por que está errado: as estatísticas freqüentistas não são usadas dessa maneira há cerca de sete décadas. Com testes sequenciais frequentistas, você não precisa de uma duração fixa predeterminada.
A verdade: os testes sequenciais, que são mais populares hoje em dia, exigem um tamanho máximo de amostra para equilibrar os erros tipo I e tipo II, mas o tamanho real da amostra usado varia de caso para caso, dependendo do resultado observado.
Então, você deve escolher Bayesiano ou Frequentista? Há um lugar para ambos.
Não há necessidade de escolher um lado. Ambos os métodos têm seu lugar. Por exemplo, um projeto de longo prazo que usa antecedentes atualizados e precisa de resultados rápidos se ajusta melhor com a abordagem bayesiana.
O método Frequentista, por outro lado, é mais adequado para projetos que exigem uma quantidade significativa de repetibilidade em seus resultados. Como escrever software que muitas pessoas com muitos conjuntos de dados usarão.
Como Cassie Kozyrkov, chefe de inteligência de decisão do Google, diz: “A estatística é a ciência de mudar sua mente sob incerteza”.
Em seu vídeo de resumo de Estatísticas Bayesianas vs Frequentistas, ela disse:
“Você pode pegar aquele debate frequencial e bayesiano e reduzir tudo sobre o que você está mudando de ideia. Frequentistas mudam de ideia sobre as ações, eles têm uma ação padrão preferida – talvez eles não tenham nenhuma crença – mas eles têm uma ação que eles gostam por ignorância e então eles perguntam: “Minhas evidências [ou dados] mudam minha mente sobre essa ação?” “Eu me sinto ridículo fazendo isso com base em minhas evidências?”
Bayesianos, por outro lado, mudam de ideia de uma maneira diferente. Eles começam com uma opinião, uma opinião pessoal expressa matematicamente, chamada de prévia, e então perguntam: “Qual é a opinião sensata que devo ter depois de incorporar algumas evidências?” E assim os Frequentistas mudam de opinião sobre as ações, os Bayesianos mudam de opinião sobre as crenças.
E dependendo de como você deseja enquadrar sua tomada de decisão, você pode preferir ir com um campo em vez do outro.”
No final, estamos todos caminhando para conclusões semelhantes – a diferença está em como essas conclusões são apresentadas a você.
Se freqüentista e inferência bayesiana fossem funções de programação, com entradas sendo problemas estatísticos, então as duas seriam diferentes no que retornam ao usuário. A função de inferência frequentista retornaria um número, representando uma estimativa (normalmente uma estatística de resumo como a média da amostra etc.), enquanto a função Bayesiana retornaria probabilidades.
Trecho do livro “Probabilistic Programming & Bayesian Methods for Hackers
O que não está muito certo é a afirmação de que um dá mais resultados práticos do que o outro.
Dica importante
A estatística Bayesiana em testes A/B consiste em 4 etapas distintas:
- Identifique sua distribuição anterior
- Escolha um modelo estatístico que reflita suas crenças
- Execute o experimento
- Use os resultados para atualizar suas crenças e calcular uma distribuição posterior
Seus resultados apontarão para probabilidades perspicazes. Assim, você saberá qual variante tem a maior probabilidade de ser a melhor, sua perda esperada e sua elevação esperada.
Eles geralmente são interpretados para você pela maioria das ferramentas de teste A/B usando estatísticas Bayesianas. Mas um experimentador completo realizará uma análise pós-teste para entender melhor esses resultados.
Porque você chegou até aqui, aqui está um fato divertido para você: você conhece o retrato de Thomas Bayes com o qual todos estão familiarizados? Este:

Ninguém tem 100% de certeza que é ele.