Błędy typu I i typu II: nieuniknione błędy w optymalizacji

Błędy typu I i typu II zdarzają się, gdy błędnie dostrzegasz zwycięzców w swoich eksperymentach lub ich nie zauważasz. W przypadku obu błędów kończysz z tym, co wydaje się działać lub nie. I nie z prawdziwymi wynikami.

Błędna interpretacja wyników testów nie tylko prowadzi do błędnych działań optymalizacyjnych, ale może również wykoleić Twój program optymalizacyjny na dłuższą metę.

Najlepszy czas na wyłapanie tych błędów jest przed ich popełnieniem! Zobaczmy więc, jak uniknąć błędów typu I i II podczas eksperymentów optymalizacyjnych.

Ale wcześniej spójrzmy na hipotezę zerową… ponieważ to błędne odrzucenie lub nieodrzucenie hipotezy zerowej powoduje błędy typu I i II .

Hipoteza zerowa: ​H0

Gdy stawiasz hipotezę eksperymentu, nie od razu sugerujesz, że proponowana zmiana przesunie pewne dane.

Zaczynasz od stwierdzenia, że ​​proponowana zmiana w ogóle nie wpłynie na daną metrykę — że nie są one powiązane.

To jest twoja hipoteza zerowa (H0). H0 zawsze oznacza brak zmian. To jest to, w co domyślnie wierzysz… dopóki (i jeśli) Twój eksperyment tego nie obali.

Twoja alternatywna hipoteza (Ha lub H1) mówi, że nastąpiła pozytywna zmiana. H0 i Ha są zawsze matematycznymi przeciwieństwami. Ha to ta, w której oczekujesz, że proponowana zmiana przyniesie zmianę, jest to twoja alternatywna hipoteza — i to właśnie testujesz w swoim eksperymencie.

Na przykład, jeśli chcesz przeprowadzić eksperyment na swojej stronie cenowej i dodać do niej inną metodę płatności, najpierw postaw hipotezę zerową: Dodatkowa metoda płatności nie będzie miała wpływu na sprzedaż. Twoja alternatywna hipoteza brzmiałaby: Dodatkowa metoda płatności ZWIĘKSZA sprzedaż.

Przeprowadzenie eksperymentu w rzeczywistości kwestionuje hipotezę zerową lub status quo.

Błędy typu I i typu II zdarzają się, gdy błędnie odrzucasz lub nie odrzucasz hipotezy zerowej.

Zrozumienie błędów typu I

Błędy typu I są znane jako fałszywe alarmy lub błędy alfa.

W przypadku błędu typu I podczas testowania hipotez test lub eksperyment optymalizacyjny * WYDAJE SIĘ UDANY* i (błędnie) dochodzisz do wniosku, że testowana odmiana wypada inaczej (lepiej lub gorzej) niż oryginalna.

W błędach typu I widzisz wzrosty lub spadki — które są tylko tymczasowe i prawdopodobnie nie utrzymają się w dłuższej perspektywie — i w końcu odrzucasz swoją hipotezę zerową (i akceptujesz hipotezę alternatywną).

Błędne odrzucenie hipotezy zerowej może się zdarzyć z różnych powodów, ale wiodącą jest praktyka zerkania (tj. patrzenie na wyniki w międzyczasie lub podczas trwania eksperymentu). I wywoływanie testów wcześniej, niż osiągnięto ustawione kryteria zatrzymania.

Wiele metodologii testowania odradza praktykę podglądania, ponieważ patrzenie na wyniki pośrednie może prowadzić do błędnych wniosków, co skutkuje błędami typu I.

Oto jak możesz zrobić błąd typu I:

Załóżmy, że optymalizujesz stronę docelową swojej witryny B2B i stawiasz hipotezę, że dodanie do niej odznak lub nagród zmniejszy niepokój potencjalnych klientów, zwiększając w ten sposób współczynnik wypełniania formularzy (co skutkuje większą liczbą potencjalnych klientów).

Twoja hipoteza zerowa dla tego eksperymentu brzmi: dodawanie plakietek nie ma wpływu na wypełnianie formularzy.

Kryterium zakończenia takiego eksperymentu jest zwykle pewien okres i/lub po X konwersji na określonym poziomie istotności statystycznej. Zwykle optymalizatorzy starają się osiągnąć 95-procentowy statystyczny znak ufności, ponieważ daje to 5% szansy na popełnienie błędu typu I, który jest uważany za wystarczająco niski dla większości eksperymentów optymalizacyjnych. Ogólnie rzecz biorąc, im wyższy jest ten wskaźnik, tym mniejsze prawdopodobieństwo popełnienia błędów typu I.

Poziom ufności, do którego dążysz, określa, jakie będzie prawdopodobieństwo wystąpienia błędu I typu (α).

Jeśli więc dążysz do 95% poziomu ufności, twoja wartość α wynosi 5%. Tutaj zgadzasz się, że istnieje 5% szans, że Twój wniosek może być błędny.

W przeciwieństwie do tego, jeśli w eksperymencie przejdziesz z 99% poziomem ufności, prawdopodobieństwo wystąpienia błędu I typu spadnie do 1%.

Załóżmy, że w przypadku tego eksperymentu stajesz się zbyt niecierpliwy i zamiast czekać na zakończenie eksperymentu, patrzysz na pulpit nawigacyjny narzędzia testowego (peek!) po zaledwie jednym dniu. Zauważasz „pozorny” wzrost — współczynnik wypełnienia formularzy wzrósł aż o 29,2% przy 95% poziomie ufności.

I BAM…

… przerywasz eksperyment.

… odrzucić hipotezę zerową (że odznaki nie miały wpływu na sprzedaż).

… zaakceptuj alternatywną hipotezę (że odznaki zwiększyły sprzedaż).

… i uruchom wersję z odznakami.

Jednak mierząc liczbę potencjalnych klientów w ciągu miesiąca, okazuje się, że liczba ta jest prawie porównywalna z liczbą zgłoszoną w oryginalnej wersji. W końcu odznaki nie miały większego znaczenia. I że hipoteza zerowa została prawdopodobnie odrzucona na próżno.

To, co się tutaj wydarzyło, polegało na tym, że zakończyłeś eksperyment zbyt wcześnie i odrzuciłeś hipotezę zerową i zakończyłeś z fałszywym zwycięzcą — popełniając błąd typu I.

Unikanie błędów typu I w eksperymentach

Pewnym sposobem na zmniejszenie szans na trafienie w błąd typu I jest wyższy poziom ufności. Dopuszczalny jest 5% poziom istotności statystycznej (co przekłada się na poziom ufności statystycznej 95%). Większość optymalizatorów postawiłaby na taki zakład, ponieważ tutaj poniesiesz porażkę w mało prawdopodobnym zakresie 5%.

Oprócz ustawienia wysokiego poziomu ufności ważne jest przeprowadzanie testów wystarczająco długo. Kalkulatory czasu trwania testu mogą powiedzieć, jak długo musisz uruchomić test (po uwzględnieniu między innymi określonych wielkości efektu). Jeśli pozwolisz, aby eksperyment przebiegał zgodnie z zamierzonym przebiegiem, znacznie zmniejszysz prawdopodobieństwo napotkania błędu typu 1 (biorąc pod uwagę wysoki poziom ufności). Czekanie na osiągnięcie statystycznie istotnych wyników gwarantuje, że prawdopodobieństwo (zwykle 5%) odrzucenia hipotezy zerowej i popełnienia błędu I typu jest niewielkie. Innymi słowy, użyj dobrej wielkości próby, ponieważ jest to kluczowe dla uzyskania statystycznie istotnych wyników.

To wszystko dotyczyło błędów typu I, które są związane z poziomem ufności (lub istotności) w twoich eksperymentach. Ale jest też inny rodzaj błędu, który może wkraść się do twoich testów – błędy typu II.

Zrozumienie błędów typu II

Błędy typu II nazywane są błędami fałszywie ujemnymi lub błędami beta.

W przeciwieństwie do błędu typu I, w przypadku błędu typu II, eksperyment *WYDAJE SIĘ NIEUDANY (LUB NIEKONKLUZYJNY)* i (błędnie) wnioskujesz, że testowana odmiana nie różni się niczym od oryginał.

W błędach typu II nie widzisz rzeczywistych wzrostów lub spadków i nie udaje ci się odrzucić hipotezy zerowej i hipotezy alternatywnej.

Oto jak możesz popełnić błąd typu II:

Wracając do tej samej strony B2B od góry…

Załóżmy więc, że tym razem stawiasz hipotezę, że dodanie oświadczenia o zgodności z RODO w widocznym miejscu u góry formularza zachęci więcej potencjalnych klientów do jego wypełnienia (co spowoduje zwiększenie liczby potencjalnych klientów).

W związku z tym Twoja hipoteza zerowa dla tego eksperymentu brzmi: Oświadczenie o zgodności z RODO nie ma wpływu na wypełnianie formularzy.

Alternatywna hipoteza dla tego samego brzmi: Oświadczenie o zgodności z RODO skutkuje większą liczbą wypełnień formularzy.

Siła statystyczna testu określa, jak dobrze może wykryć różnice w wydajności wersji oryginalnej i testowej, jeśli istnieją jakiekolwiek odchylenia. Tradycyjnie optymalizatorzy starają się osiągnąć 80% statystycznej potęgi, ponieważ im wyższa jest ta metryka, tym mniejsze są szanse popełnienia błędów typu II.

Moc statystyczna przyjmuje wartość od 0 do 1 (i często jest wyrażana w %) i kontroluje prawdopodobieństwo błędu typu II (β); oblicza się jako: 1 – β

Im wyższa moc statystyczna twojego testu, tym mniejsze będzie prawdopodobieństwo napotkania błędów typu II.

Jeśli więc eksperyment ma moc statystyczną 10%, może być dość podatny na błąd typu II. Natomiast jeśli eksperyment ma moc statystyczną 80%, prawdopodobieństwo popełnienia błędu typu II będzie znacznie mniejsze.

Ponownie uruchamiasz test, ale tym razem nie zauważasz żadnego znaczącego wzrostu liczby wypełnień formularzy. Obie wersje zgłaszają prawie podobne konwersje. Z tego powodu przerywasz eksperyment i kontynuujesz oryginalną wersję bez oświadczenia o zgodności z RODO.

Jednak w miarę zagłębiania się w dane o potencjalnych klientach z okresu eksperymentu okazuje się, że chociaż liczba potencjalnych klientów z obu wersji (oryginalnej i prowokującej) wydawała się identyczna, wersja RODO zapewniła dobry, znaczący wzrost liczby potencjalnych klientów z Europy. (Oczywiście można było użyć kierowania na odbiorców, aby pokazać eksperyment tylko potencjalnym potencjalnym klientom z Europy – ale to już inna historia).

To, co się tutaj wydarzyło, polegało na tym, że zakończyłeś test zbyt wcześnie, nie sprawdzając, czy osiągnąłeś wystarczającą moc – popełniając błąd typu II.

Unikanie błędów typu II w eksperymentach

Aby uniknąć błędów typu II, przeprowadzaj testy z dużą mocą statystyczną. Spróbuj skonfigurować eksperymenty tak, aby osiągnąć co najmniej 80% statystycznej potęgi. Jest to akceptowalny poziom mocy statystycznej dla większości eksperymentów optymalizacyjnych. Dzięki niemu możesz mieć pewność, że przynajmniej w 80% przypadków poprawnie odrzucisz fałszywą hipotezę zerową.

Aby to zrobić, musisz przyjrzeć się czynnikom, które do tego dodają.

Największym z nich jest wielkość próby (biorąc pod uwagę wielkość obserwowanego efektu). Wielkość próbki jest bezpośrednio powiązana z mocą testu. Ogromna wielkość próbki oznacza test dużej mocy. Słabe testy są bardzo podatne na błędy typu II, ponieważ Twoje szanse na wykrycie różnic w wynikach Twojego pretendenta i oryginalnych wersji znacznie się zmniejszają, szczególnie w przypadku niskich MEI (więcej na ten temat poniżej). Tak więc, aby uniknąć błędów typu II, poczekaj, aż test zgromadzi wystarczającą moc, aby zminimalizować błędy typu II. Idealnie, w większości przypadków, chciałbyś osiągnąć moc co najmniej 80%.

Innym czynnikiem jest minimalny efekt zainteresowania (MEI) , który jest celem eksperymentu. MEI (zwany również MDE) to minimalna wielkość różnicy, którą chciałbyś wykryć w danym KPI. Jeśli ustawisz niski MEI (na przykład przyglądając się wzrostowi 1,5%), twoje szanse na napotkanie błędu typu II wzrosną, ponieważ wykrycie małych różnic wymaga znacznie większych rozmiarów próbek (aby uzyskać wystarczającą moc).

I na koniec, należy zauważyć, że istnieje odwrotna zależność między prawdopodobieństwem popełnienia błędu typu I (α) a prawdopodobieństwem popełnienia błędu typu II (β). Na przykład, jeśli zmniejszysz wartość α, aby zmniejszyć prawdopodobieństwo popełnienia błędu typu I (powiedzmy, że ustawisz α na 1%, co oznacza poziom ufności 99%), moc statystyczną eksperymentu (lub jego zdolność, β , wykrycia różnicy, jeśli istnieje) również się zmniejsza, zwiększając w ten sposób prawdopodobieństwo wystąpienia błędu typu II.

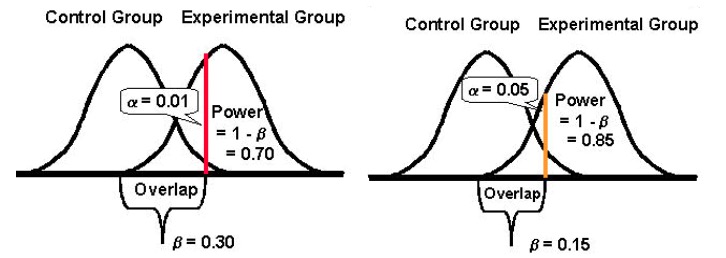
Większa akceptacja któregokolwiek z błędów: Typ I i ​​II (i osiągnięcie równowagi)

Obniżenie prawdopodobieństwa jednego rodzaju błędu zwiększa prawdopodobieństwo drugiego typu (pod warunkiem, że wszystko inne pozostaje takie samo).

Musisz więc odpowiedzieć na pytanie, jaki typ błędu możesz być bardziej tolerancyjny.

Z jednej strony popełnienie błędu typu I i wprowadzenie zmiany dla wszystkich użytkowników może kosztować konwersje i przychody — co gorsza, może też być zabójcą konwersji.

Z drugiej strony popełnienie błędu typu II i niewdrożenie zwycięskiej wersji dla wszystkich użytkowników może ponownie kosztować konwersje, które w przeciwnym razie można by wygrać.

Niezmiennie oba błędy mają swoją cenę.

Jednak w zależności od eksperymentu jeden może być dla ciebie bardziej akceptowalny niż drugi. Ogólnie rzecz biorąc, testerzy uważają, że błąd typu I jest około cztery razy poważniejszy niż błąd typu II .

Jeśli chciałbyś przyjąć bardziej wyważone podejście, statystyk Jacob Cohen sugeruje, że powinieneś sięgnąć po moc statystyczną 80%, która daje „rozsądną równowagę między ryzykiem alfa i beta. ” (80% mocy jest również standardem dla większości narzędzi testowych.)

A jeśli chodzi o istotność statystyczną, standardem jest 95%.

Zasadniczo chodzi o kompromis i poziom ryzyka, który jesteś w stanie tolerować. Jeśli naprawdę chcesz zminimalizować szanse na oba błędy, możesz wybrać poziom ufności 99% i moc 99%. Ale to by oznaczało, że będziesz pracował z niemożliwie ogromnymi rozmiarami próbek przez okresy, które wydają się wiecznie długie. Poza tym nawet wtedy pozostawiałbyś trochę miejsca na błędy.

Co jakiś czas błędnie zakończysz eksperyment. Ale to część procesu testowania — opanowanie statystyk testów A/B zajmuje trochę czasu. Badanie i ponowne testowanie lub śledzenie udanych lub nieudanych eksperymentów jest jednym ze sposobów potwierdzenia wyników lub odkrycia, że ​​popełniłeś błąd.