Sieć neuronowa pojedynczego neuronu w Pythonie — z matematyczną intuicją

Zbudujmy prostą sieć — bardzo, bardzo prostą, ale kompletną sieć — z pojedynczą warstwą. Tylko jedno wejście — i jeden neuron (który jest również wyjściem), jedna waga, jeden błąd.

Najpierw uruchommy kod, a potem przeanalizujmy część po części

Sklonuj projekt Github lub po prostu uruchom następujący kod w swoim ulubionym IDE.

Jeśli potrzebujesz pomocy w skonfigurowaniu IDE, opisałem ten proces tutaj.

Jeśli wszystko pójdzie dobrze, otrzymasz ten wynik:

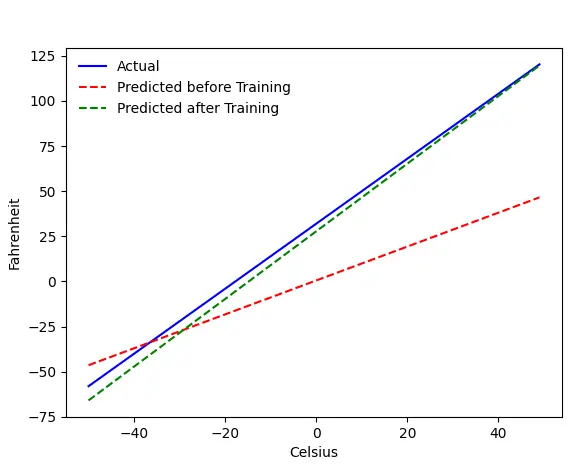
Problem — Fahrenheit z Celsjusza

Wyszkolimy naszą maszynę, aby przewidywała stopnie Fahrenheita z Celsjusza. Jak możesz zrozumieć z kodu (lub wykresu), niebieska linia jest rzeczywistą relacją Celsjusza-Fahrenheita. Czerwona linia to relacja przewidywana przez naszą maszynkę bez treningu. Na koniec trenujemy maszynę, a zielona linia to zapowiedź po treningu.

Spójrz na Wiersz nr 65–67 — przed i po treningu przewiduje się przy użyciu tej samej funkcji ( get_predicted_fahrenheit_values() ). Więc co robi magic train()? Dowiedzmy Się.

Struktura sieci

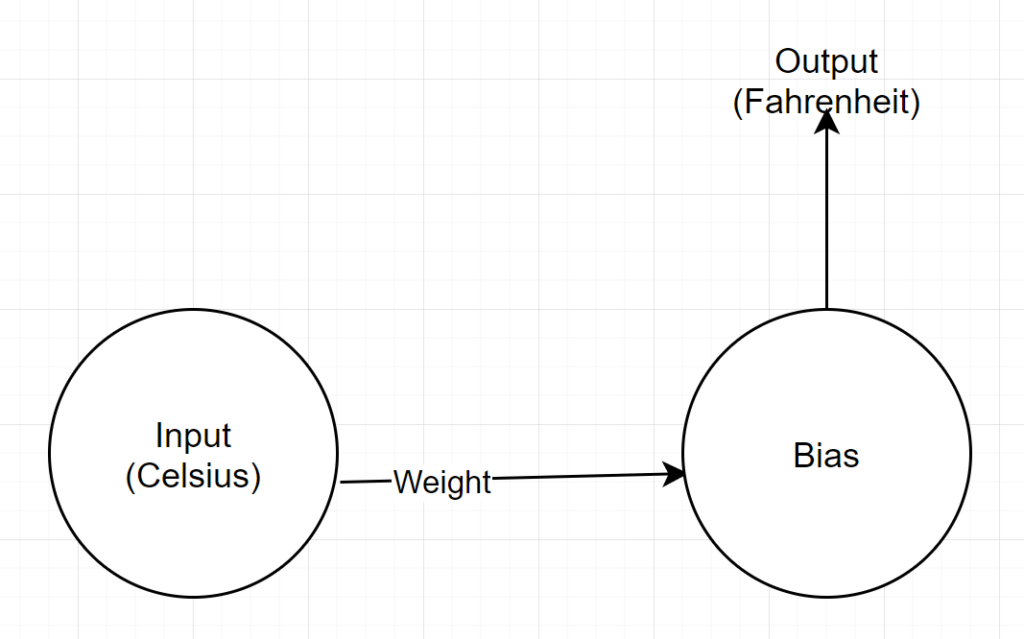
Dane wejściowe: liczba reprezentująca stopnie Celsjusza

Waga: pływak reprezentujący wagę

Bias: zmiennoprzecinkowa reprezentująca stronniczość

Dane wyjściowe: zmiennoprzecinkowa reprezentująca przewidywany stopień Fahrenheita

Mamy więc w sumie 2 parametry — 1 wagę i 1 odchylenie

Analiza kodu

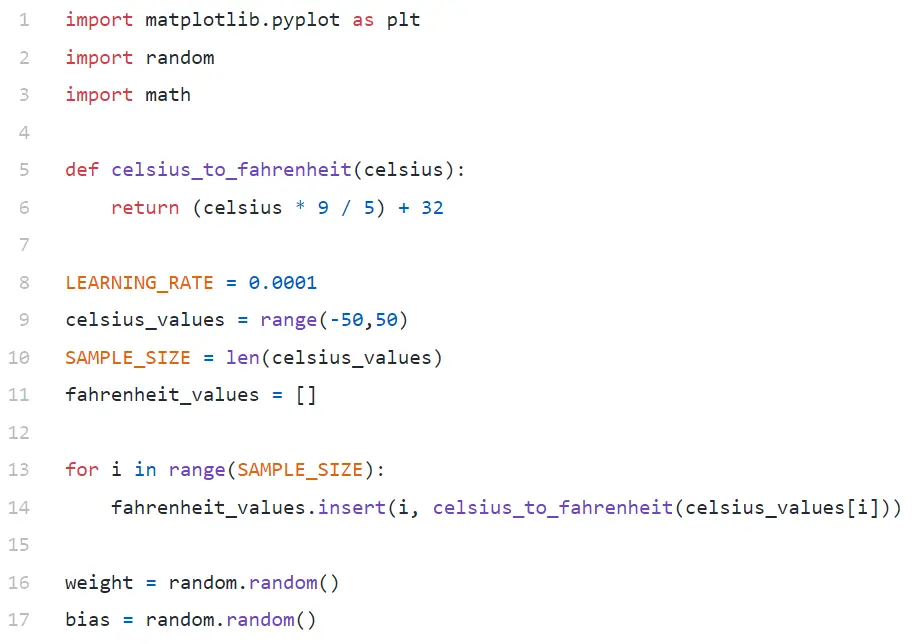
W wierszu nr 9 generujemy tablicę 100 liczb z zakresu od -50 do +50 (z wyłączeniem 50 — funkcja zakresu wyklucza górną wartość graniczną).

W wierszach nr 11–14 generujemy stopnie Fahrenheita dla każdej wartości w stopniach Celsjusza.

W wierszach nr 16 i 17 inicjujemy wagę i odchylenie.

pociąg()

Prowadzimy tutaj 10000 iteracji szkoleń. Każda iteracja składa się z:

1. dalej (linia nr 57) przejść
2. przejście wstecz (linia nr 58)
3. update_parameters (linia nr 59)

Jeśli jesteś nowy w Pythonie, może to wyglądać trochę dziwnie — funkcje Pythona mogą zwracać wiele wartości jako krotka .

Zauważ, że update_parameters jest jedyną rzeczą, która nas interesuje. Wszystko, co robimy tutaj, to ocena parametrów tej funkcji, które są gradientami (poniżej wyjaśnimy, czym są gradienty) naszej wagi i odchylenia.

1. grad_weight: pływak reprezentujący gradient wagi
2. grad_bias: zmiennoprzecinkowa reprezentująca gradient odchylenia

Otrzymujemy te wartości, wywołując wstecz, ale wymaga to wyjścia, które otrzymujemy, wywołując dalej w wierszu nr 57.

Naprzód()

Zauważ, że tutaj celsius_values ​​i fahrenheit_values ​​są tablicami po 100 wierszy:

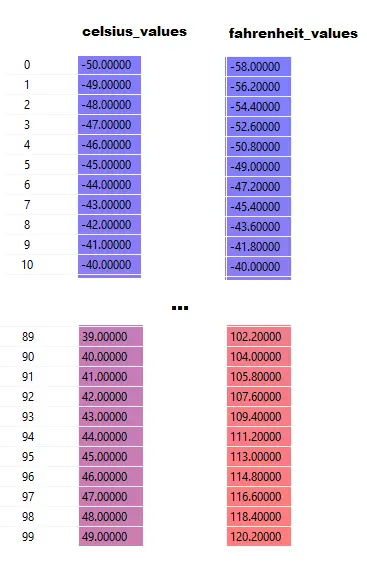
Po wykonaniu linii nr 20–23, dla wartości w stopniach Celsjusza, powiedz 42

wyjście = 42 * waga + odchylenie

Tak więc dla 100 elementów w celsius_values ​​wynik będzie tablicą 100 elementów dla każdej odpowiadającej wartości celsjusza.

Linia nr 25–30 oblicza straty za pomocą funkcji straty średniej kwadratowej (MSE), która jest po prostu wymyślną nazwą kwadratu wszystkich różnic podzielonych przez liczbę próbek (w tym przypadku 100).

Mała strata oznacza lepsze przewidywanie. Jeśli utrzymasz straty drukowania w każdej iteracji, zobaczysz, że zmniejsza się wraz z postępem treningu.

Wreszcie w wierszu nr 31 zwracamy przewidywaną wydajność i stratę.

do tyłu

Jesteśmy zainteresowani tylko aktualizacją naszej wagi i odchylenia. Aby zaktualizować te wartości, musimy znać ich gradienty i właśnie to tutaj obliczamy.

Zauważ, że gradienty są obliczane w odwrotnej kolejności. Najpierw obliczany jest gradient wyjścia, a następnie wagi i odchylenia, stąd nazwa „propagacja wsteczna”. Powodem jest to, że aby obliczyć gradient wagi i odchylenia, musimy znać gradient wyjścia — abyśmy mogli go użyć we wzorze reguły łańcucha .

Przyjrzyjmy się teraz, czym są reguły gradientu i łańcucha.

Gradient

Dla uproszczenia rozważmy, że mamy tylko jedną wartość wartości_celsjusza i wartości_fahrenheita , odpowiednio 42 i 107,6 .

Teraz podział obliczeń w wierszu nr 30 wygląda następująco:

strata = (107,6 — (42 * waga + odchylenie))² / 1

Jak widzisz, strata zależy od 2 parametrów — wagi i odchylenia. Rozważ wagę. Wyobraź sobie, że zainicjalizowaliśmy go losową wartością, powiedzmy 0,8, i po przeanalizowaniu powyższego równania otrzymamy 123,45 jako wartość straty . Na podstawie tej wartości utraty musisz zdecydować, w jaki sposób zaktualizujesz wagę. Czy powinieneś zrobić to 0,9 czy 0,7?

Musisz zaktualizować wagę w taki sposób, aby w kolejnej iteracji uzyskać niższą wartość straty (pamiętaj, że minimalizacja strat jest ostatecznym celem). Jeśli więc zwiększenie wagi zwiększa utratę wagi, zmniejszymy ją. A jeśli zwiększenie wagi zmniejszy utratę, będziemy ją zwiększać.

Teraz pytanie, skąd wiemy, czy zwiększenie wagi zwiększy czy zmniejszy utratę. Tutaj wkracza gradient . Mówiąc ogólnie, gradient jest definiowany przez pochodną. Pamiętaj ze swojego rachunku różniczkowego w szkole średniej, ∂y/∂x (który jest pochodną cząstkową/gradientem y względem x) wskazuje, jak zmieni się y z niewielką zmianą x.

Jeśli ∂y/∂x jest dodatnie, oznacza to, że mały przyrost x zwiększy y.

Jeśli ∂y/∂x jest ujemne, oznacza to, że mały przyrost x zmniejszy y.

Jeśli ∂y/∂x jest duże, mała zmiana x spowoduje dużą zmianę y.

Jeśli ∂y/∂x jest małe, mała zmiana x spowoduje małą zmianę y.

Tak więc z gradientów otrzymujemy 2 informacje. W jakim kierunku należy zaktualizować parametr (zwiększyć lub zmniejszyć) i o ile (duży lub mały).

Zasada łańcuchowa

Mówiąc nieformalnie, zasada łańcucha mówi:

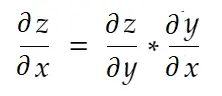
Rozważmy przykład wagi powyżej. Musimy obliczyć grad_weight , aby zaktualizować tę wagę, która zostanie obliczona przez:

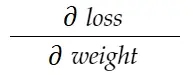
Za pomocą formuły reguły łańcucha możemy ją wyprowadzić:

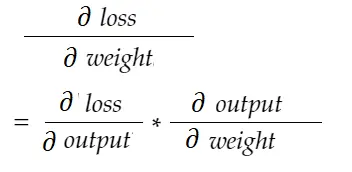
Podobnie, gradient dla stronniczości:

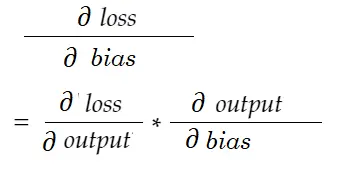
Narysujmy diagram zależności.

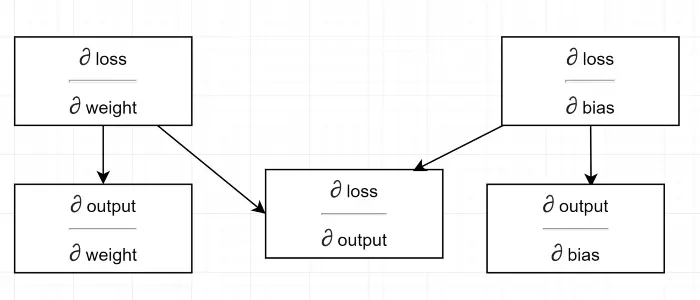
Zobacz wszystkie obliczenia zależą od gradientu wydajności (∂ strata/∂ wydajność) . Dlatego najpierw obliczamy go na backpassie (linia 34–36).

W rzeczywistości w wysokopoziomowych frameworkach ML, na przykład w PyTorch, nie musisz pisać kodów dla backpassu! Podczas przejścia do przodu tworzy wykresy obliczeniowe, a podczas przejścia wstecznego przechodzi przez przeciwny kierunek na wykresie i oblicza gradienty za pomocą reguły łańcuchowej.

∂ strata / ∂ wydajność

Definiujemy tę zmienną przez grad_output w kodzie, który obliczyliśmy w wierszu 34–36. Znajdźmy przyczynę formuły, której użyliśmy w kodzie.

Pamiętaj, że razem wprowadzamy wszystkie 100 celsjusza do maszyny. Tak więc grad_output będzie tablicą 100 elementów, z których każdy zawiera gradient wyjścia dla odpowiedniego elementu w celsius_values ​​. Dla uproszczenia rozważmy, że w celsius_values ​​są tylko 2 elementy.

Tak więc, przełamując linię # 30,

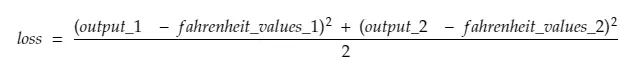
gdzie,

output_1 = wartość wyjściowa dla pierwszej wartości celsjusza

output_2 = wartość wyjściowa dla drugiej wartości celsjusza

fahreinheit_values_1 = Rzeczywista wartość w stopniach Fahreinheita dla pierwszej wartości w stopniach Celsjusza

fahreinheit_values_1 = Rzeczywista wartość w stopniach Fahreinheita dla drugiej wartości w stopniach Celsjusza

Teraz zmienna wynikowa grad_output będzie zawierać 2 wartości — gradient output_1 i output_2, co oznacza:

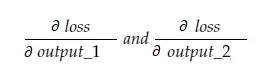
Obliczmy tylko gradient wyjścia_1, a następnie możemy zastosować tę samą regułę dla pozostałych.

Czas na rachunek!

Czyli to samo, co wiersz 34–36.

Gradient wagi

Wyobraź sobie, że mamy tylko jeden element w celsius_values. Teraz:

Który jest taki sam jak Linia nr 38-40. Dla 100 celsius_values ​​wartości gradientu dla każdej z wartości zostaną zsumowane. Oczywistym pytaniem byłoby, dlaczego nie zmniejszamy wyniku (tj. dzielimy przez SAMPLE_SIZE). Ponieważ przed aktualizacją parametrów mnożymy wszystkie gradienty z małym współczynnikiem, nie jest to konieczne (patrz ostatnia sekcja Aktualizacja parametrów).

Gradient odchylenia

Który jest taki sam jak Linia nr 42. Podobnie jak gradienty wag, te wartości dla każdego ze 100 wejść są sumowane. Ponownie, jest to w porządku, ponieważ gradienty są mnożone przez mały współczynnik przed aktualizacją parametrów.

Aktualizowanie parametrów

Na koniec aktualizujemy parametry. Zauważ, że gradienty pomnożone przez mały współczynnik (LEARNING_RATE) przed odjęciem, aby trening był stabilny. Duża wartość LEARNING_RATE spowoduje problem z przekroczeniem , a bardzo mała wartość spowolni trening, co może wymagać znacznie większej liczby iteracji. Powinniśmy znaleźć dla niego optymalną wartość przy odrobinie prób i błędów. Istnieje wiele zasobów internetowych na ten temat, w tym ten, aby dowiedzieć się więcej o nauce Rate.

Zauważ, że dokładna kwota, którą dostosowujemy, nie jest bardzo krytyczna. Na przykład, jeśli nieco dostroisz LEARNING_RATE, zmienne descent_grad_weight i descent_grad_bias (linia nr 49–50) zostaną zmienione, ale maszyna może nadal działać. Ważną rzeczą jest upewnienie się, że te wartości są uzyskiwane przez zmniejszanie gradientów z tym samym współczynnikiem (w tym przypadku LEARNING_RATE). Innymi słowy, „utrzymanie proporcjonalnego spadku gradientów” ma większe znaczenie niż „jak bardzo spadają ”.

Zauważ również, że te wartości gradientów są w rzeczywistości sumą gradientów obliczonych dla każdego ze 100 wejść. Ale ponieważ są one skalowane z tą samą wartością, jest w porządku, jak wspomniano powyżej.

Aby zaktualizować parametry, musimy je zadeklarować za pomocą słowa kluczowego global (w linii nr 47).

Dokąd się udać?

Kod byłby znacznie mniejszy, gdyby zastąpić pętle for listą składaną w sposób pythoniczny. Spójrz na to teraz — zrozumienie nie zajmie więcej niż kilka minut.

Jeśli do tej pory wszystko zrozumiałeś, prawdopodobnie jest to dobry moment, aby zobaczyć wnętrze prostej sieci z wieloma neuronami/warstwami — oto artykuł.