Poczuj rachunek ze swoim zmysłem programowania

Wierzę, że ludzie, którzy potrafią kodować — mają zdolność rozumienia bardziej skomplikowanych pojęć niż rachunek różniczkowy. Jednym z powodów, dla których jest wielu utalentowanych programistów, którzy wciąż zmagają się z rachunkiem różniczkowym, nie jest to, że jest to trudne. Dzieje się tak głównie dlatego, że nauczono nas tego w niewłaściwy sposób (wraz z wieloma innymi tematami).

Jeśli w swoim życiu zajmowałeś się kodowaniem — nawet niektórymi zabawkowymi ćwiczeniami, takimi jak generowanie liczb pierwszych, być może robiłeś już podobne rzeczy, które dzieją się w rachunku różniczkowym, ale nigdy nie miałeś okazji się z nimi związać.

Celem tego pisania nie jest nauczenie cię rachunku różniczkowego ani programowania — ale pomoc w łączeniu kilku kropek.

Za chwilę przejdę do kodowania. Ale pozwólcie, że wcześniej omówię trochę tła.

Tempo zmian

Rachunek różniczkowy mówi o „tempie zmian”. Spróbujmy zrozumieć, co to znaczy.

W przypadku zmiany zmiennej (x) szybkość zmiany funkcji jest po prostu zmianą funkcji podzieloną przez zmianę x. Niech wizualizuj z rzeczywistymi liczbami:

Rozważ 2 punkty x=2 i x=6 oraz funkcję y=f(x) = x².

Weź również pod uwagę dx = odległość między tymi 2 punktami na osi X. A dy to odległość między wartościami y dla tych wartości x.

Wtedy tempo zmian w y od x=2 do x=6 wynosi

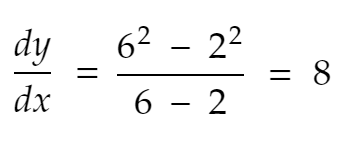
Pochodna

Teraz — pochodna dy/dx to tempo zmian w y dla nieskończenie małej zmiany w x. Ponieważ ta odległość (6–2=4) nie jest nieskończenie mała — nawet bliska, nie możemy nazwać powyższego równania pochodną. Na razie wybierzmy mniejszą liczbę, 0,1 .

Gdy x = 0, y = x² = 0² = 0.

Najbliższy sąsiad w kierunku dodatnim, x = 0,1. Tam y staje się 0,1² = 0,01.

Więc,

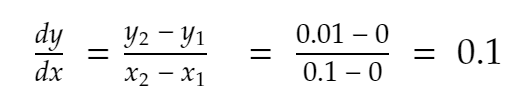
Spróbujmy jeszcze raz. Najbliższy sąsiad 0,1 w kierunku dodatnim, x = 0,2. Zatem y staje się 0,2² = 0,04. Więc,

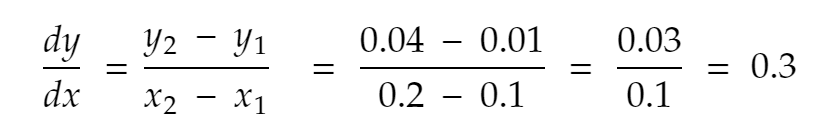
Jeśli powtórzymy proces jeszcze kilka razy, otrzymamy:

Oto plik Excela, jeśli chcesz się z nim bawić.

dx (co jest naszą fikcyjną, nieskończenie małą odległością między dwoma sąsiednimi punktami na osi x) wynosi 0,1 w naszym kontekście.

x odpowiednio rośnie.

y to po prostu x².

dy to odległość między 2 sąsiednimi wartościami y. Na przykład, gdy x= 0,1, odległość między bieżącym y (0,01) a następnym y (0,04) wynosi 0,03 — więc dy wynosi 0,03 przy x=0,1.

dy/dx to dy podzielone przez dx.

dy/dx / x to dy/dx podzielone przez x.

Teraz zauważ, że wraz ze wzrostem x ostatni wiersz zbliża się do 2, co oznacza — tempo zmiany x² względem x zbliża się dwukrotnie do x, czyli 2x .

Pamiętasz pochodną x² względem x? 2x! Znalezienie jakiegoś połączenia?

Czas kodowania

Wypróbujmy w kodzie rzeczy, o których dyskutowaliśmy do tej pory.

Zakładając, że masz już zainstalowany Python, w terminalu uruchom:

Następnie uruchom następujący kod Pythona:

Tutaj:

x : zawiera liczby od 0 do 9.

y : kolejna tablica, każdy element jest kwadratem odpowiadającego mu elementu x

dy : Kolejna tablica inicjowana zerami. W tej tablicy umieścimy odległości y.

dydx : kolejna tablica inicjowana zerami. Będzie zawierać wartość dy/dx każdego punktu.

dx : Dość oczywiste — to wielkość kroku. Odległość między 2 kolejnymi liczbami, która zmniejsza się wraz ze wzrostem ROZMIARU. Jeśli ROZMIAR = 10, dx = 1. Jeśli ROZMIAR = 100, dx = 0,1.

Po pierwsze, wyprowadzamy dy dla każdego punktu. Następnie obliczamy z tego dydx.

Zauważ, że:

Tutaj pomijamy pierwszą i ostatnią wartość. Pierwsza wartość x to 0, co spowoduje błąd dzielenia zerowego. I nie możemy obliczyć ostatniej wartości dy/dx, ponieważ nie mamy ostatniej wartości dy — ponieważ wymagałoby to następnej dostępnej wartości y, której tutaj nie mamy.

Jeśli wszystko pójdzie dobrze, otrzymasz ten wykres:

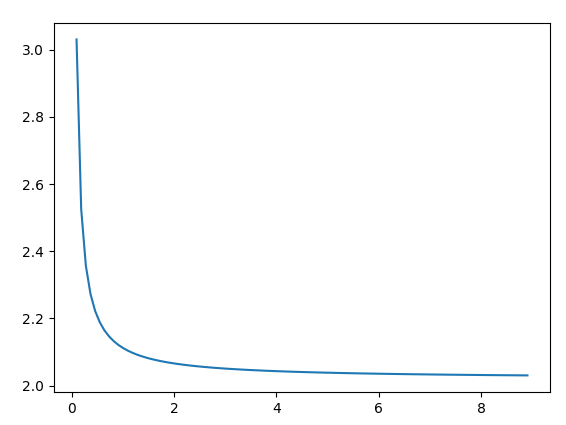
Co rozumiesz z fabuły

Jak widzisz, wykres zbliża się do 2. Zwiększ wartość ROZMIAR (co oznacza ustawienie mniejszej wartości dx) i zobacz, jak wykres szybciej zbliża się do 2.

Druga pochodna

Teraz, gdy zaszedłeś tak daleko, jeszcze tylko kilka kroków, aby zrealizować drugą pochodną, ​​która da ci intuicję dla pochodnej dowolnego rzędu.

Jak pamiętasz, druga pochodna to tempo zmian pierwszej pochodnej względem x. Mówiąc najprościej — dy/dx w drugiej pochodnej jest jak y w pierwszej pochodnej.

Zróbmy następujące modyfikacje powyższego kodu:

Zadeklaruj jeszcze 2 tablice:

d2ydx2 : Który będzie reprezentował drugą pochodną:

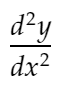
distance_dydx: Aby przedstawić odległość między wartością dy/dx między 2 sąsiednimi punktami

Oto pełny kod drugiej pochodnej:

Po obliczeniu dydx w pętli for wykonujemy kolejną pętlę, aby obliczyć drugą pochodną. Przy pewnym mądrym kodowaniu moglibyśmy obliczyć drugą pochodną w tej samej pętli (spróbuj jako ćwiczenie) — ale umieściłem je tutaj osobno dla jasności.

Zauważ też, że:

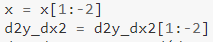
Podobnie jak w przypadku pierwszej pochodnej, tutaj również pomijamy niektóre wartości. Ostatnie 2 wartości są pomijane, ponieważ druga od ostatniej wymagałaby ostatniej wartości „pierwszej pochodnej”, której nie mogliśmy obliczyć (ponieważ nie mieliśmy dla niej wymaganej wartości y — jak opisano powyżej). Czy to oznacza, że ​​musimy pominąć ostatnie 3 wartości w przypadku trzeciej pochodnej?🤔 — to Ty musisz znaleźć.

Oto wykres wyjściowy:

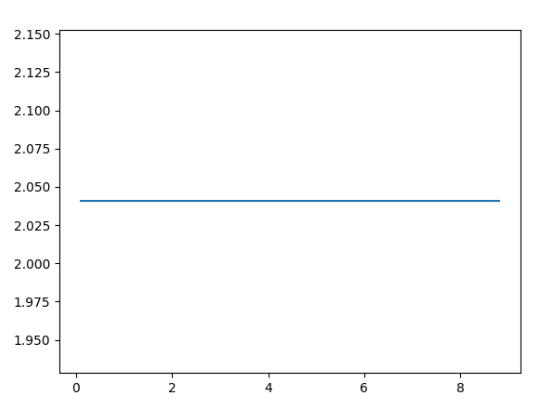
Co tu widzimy?

Jak wiecie z liceum:

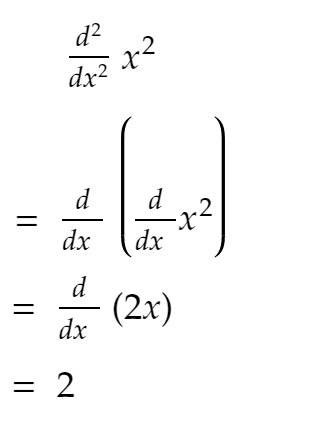
Teraz, jak widać z powyższego kodu, druga pochodna w większości pozostaje stała, a jeśli ciągle zwiększasz ROZMIAR — zbliża się do 2!

Dlaczego tempo zmian jest ważne

Możesz się zastanawiać:

— Dlaczego przechodzimy przez te wszystkie paskudne kłopoty? Jakie użyteczne informacje otrzymujemy ze stopy zmiany lub pochodnej?

— Dlaczego nie możemy po prostu podążać za tempem zmian za jakąkolwiek kwotę? Dlaczego tylko nieskończenie małe? Jakie informacje otrzymujemy z tempa zmian względem nieskończenie małych , których nie można znaleźć z tempa zmian względem większych wartości?

— Ta nieskończenie mała rzecz wygląda jak hack? Pracowaliśmy z kilkoma małymi liczbami powyżej w porządku — ale na pewno nie w rzeczywistości nieskończenie małymi.

Gdybym pozwolił sobie iść dalej, odszedłbyś, widząc długość tego artykułu i nie zaszedłbyś tak daleko. Może odpowiemy na te pytania kiedyś 😀.