Statystyki Bayesa: szybki i wolny od szumu podkład testera A/B
Opublikowany: 2022-06-23
Jak bardzo jesteś pewien swojej zdolności do interpretacji wyników dostarczonych przez Twoje narzędzie do testowania A/B?
Powiedzmy, że używasz narzędzia opartego na statystykach bayesowskich, które mówi, że „B” ma 70% szans na pokonanie „A”, więc „B” jest zwycięzcą. Czy wiesz, co to oznacza i jak powinno kształtować Twoją strategię CRO?
W tym artykule poznasz podstawy statystyk bayesowskich, które pomogą Ci odzyskać kontrolę nad testami A/B, w tym
- Bezstronny pogląd na statystyki bayesowskie
- Wady i zalety częstych gości vs Bayesa
- Przygotowanie, którego potrzebujesz, aby pewnie zinterpretować i wykorzystać wyniki testu Bayesa A/B, unikając niektórych typowych pułapek mitów.
- Co to jest statystyka bayesowska?
- Historia pochodzenia bayesowskiego
- Przykład statystyk bayesowskich zastosowanych w testach A/B
- Krótki słownik terminów bayesowskich, które mają znaczenie dla testerów A/B
- Wnioskowanie bayesowskie
- Warunkowe prawdopodobieństwo
- Rozkład prawdopodobieństwa/Rozkład prawdopodobieństwa
- Uprzednia dystrybucja przekonań
- Koniugacja
- Sprzężona Przeorów
- Funkcja straty
- Co to są statystyki częstych?
- Bayesowski vs częsty test A/B
- Ramy Frequentystyczne
- Ramy Bayesowskie
- Co właściwie mówią statystyki Bayesa w testach A/B?
- Prawdopodobieństwo bycia najlepszym (P2BB)
- Oczekiwany wzrost
- Oczekiwana strata
- Mity dotyczące statystyk Bayesa, których należy unikać
- Mit nr 1: Bayesowie wyrażają swoje założenia, częstowcy nie
- Mit 2. Metody Bayesowskie dają odpowiedzi, których naprawdę potrzebujesz
- Mit 3: Wnioskowanie bayesowskie pomaga komunikować niepewność lepiej niż wnioskowanie częsty
- Mit 4. Wyniki testów Bayesa A/B są odporne na podglądanie
- Mit nr 5 Statystyki Frequentist są nieefektywne, ponieważ trzeba czekać na ustaloną wielkość próbki
- Więc, czy powinieneś wybrać Bayesa czy Frequentistę? Jest miejsce dla obu.
- Zabrany klucz
Gotowy? Zacznijmy od podstaw.
Co to jest statystyka bayesowska?
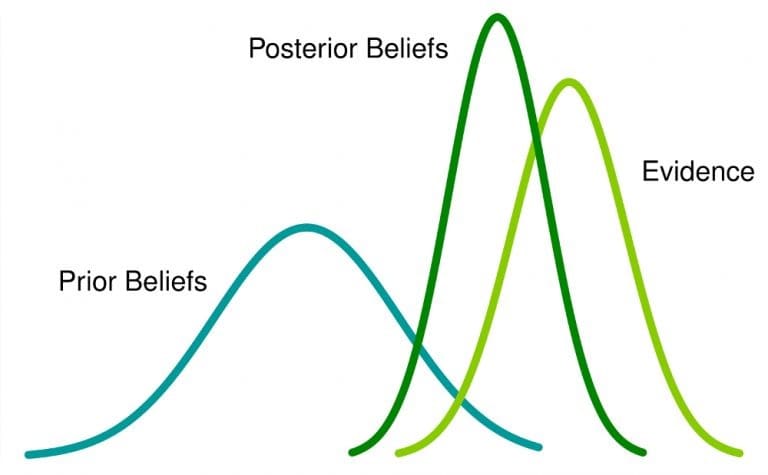
Statystyka bayesowska to podejście do analizy statystycznej oparte na twierdzeniu Bayesa, które aktualizuje przekonania o zdarzeniach w miarę gromadzenia nowych danych lub dowodów dotyczących tych zdarzeń. Tutaj prawdopodobieństwo jest miarą przekonania, że zdarzenie ma miejsce.
Co to oznacza: Jeśli masz wcześniejsze przekonanie o zdarzeniu i uzyskasz więcej informacji z nim związanych, to przekonanie zmieni się (lub przynajmniej zostanie dostosowane) do późniejszego przekonania.
Przydaje się to do zrozumienia niepewności lub podczas pracy z dużą ilością zaszumionych danych, takich jak optymalizacja współczynnika konwersji w e-commerce i uczenie maszynowe.
Wyobraźmy sobie to:
Załóżmy na przykład, że oglądasz wyścig wózków sklepowych w college'u, a potem podekscytowany widz rzuca ci wyzwanie, by założyć się, że wygra koleś w czerwonej koszulce wiozący damę w zielonej koszuli. Zastanawiasz się nad tym i kontrujesz, że zamiast tego wygrają facet z czarną kurtką i czarna bluza z kapturem.

Kolejny widz nad głową i wyszeptał ci wskazówkę: „Człowiek z czerwonej koszulki wygrał ostatnie 3 wyścigi z 4.”. Co dzieje się z twoim zakładem? Nie jesteś już zbyt pewny, prawda?
Przypuśćmy, że dowiedziałeś się również, że ostatnim razem, gdy facet w czarnej marynarce nosił swoje szczęśliwe okulary przeciwsłoneczne, wygrał. A kiedy go nie nosił, facet z czerwoną koszulką wygrywał.
Dzisiaj widzisz, że facet w czarnej marynarce nosi te okulary. Twoja wiara znów się zmienia. Masz teraz więcej wiary w swój zakład, prawda? W tej historii aktualizowałeś swoje przekonanie za każdym razem, gdy uzyskałeś dowody na nowe dane. To podejście bayesowskie.
Historia pochodzenia bayesowskiego
Kiedy wielebny Thomas Bayes po raz pierwszy pomyślał o swojej teorii, nie sądził, by była warta publikacji. Pozostało więc w jego notatkach przez ponad dekadę. Kiedy jego rodzina poprosiła Richarda Price'a o przejrzenie jego notatek, Price odkrył notatki, które stały się podstawą twierdzenia Bayesa.
Zaczęło się od eksperymentu myślowego dla Bayesa. Pomyślał o tym, żeby usiąść plecami do idealnie płaskiego i kwadratowego stołu i poprosić asystenta o rzucanie piłką na stół.
Piłka mogła wylądować w dowolnym miejscu na stole, ale Bayes pomyślał, że może odgadnąć, gdzie, aktualizując swoje przypuszczenia o nowe informacje. Kiedy piłka wylądowała na stole, asystent powiedział mu, czy wylądowała w lewo, czy w prawo, przed lub za miejscem, w którym wylądowała poprzednia piłka.
Zauważył to i nasłuchiwał, jak coraz więcej piłek spadało na stół. Dzięki dodatkowym informacjom, takim jak ta, odkrył, że może poprawić dokładność swoich domysłów przy każdym rzucie. To zrodziło pomysł zaktualizowania naszego rozumienia, gdy uzyskaliśmy więcej dowodów z obserwacji.
Bayesowskie podejście do analizy danych jest stosowane w różnych dziedzinach, takich jak nauka i inżynieria, a nawet obejmuje sport i prawo.
W randomizowanych, kontrolowanych eksperymentach online, w szczególności w testach A/B, można zastosować podejście bayesowskie w 4 krokach:
- Zidentyfikuj swoją poprzednią dystrybucję.
- Wybierz model statystyczny, który odzwierciedla Twoje przekonania.
- Uruchom eksperyment.
- Po obserwacji zaktualizuj swoje przekonania i oblicz rozkład a posteriori.
Aktualizujesz swoje przekonania za pomocą zestawu reguł zwanego algorytmem Bayesa.
Przykład statystyk bayesowskich zastosowanych w testach A/B
Zilustrujmy przykład Bayesowskiego testu A/B.
Wyobraź sobie, że przeprowadziliśmy prosty test A/B na przycisku CTA sklepu Shopify. W przypadku „A” używamy „Dodaj do koszyka”, a dla „B” używamy „Dodaj do koszyka”.
Oto, jak często bywalec podejdzie do testu.
Istnieją dwa alternatywne światy: jeden, w którym A i B nie różnią się, więc test nie wykaże żadnej różnicy w współczynniku konwersji. To jest hipoteza zerowa. A w innym świecie jest różnica, więc jeden przycisk będzie działał lepiej niż drugi.
Często bywalec założy, że żyjemy w świecie 1, w którym nie ma różnicy w przyciskach CTA, to znaczy przy założeniu, że hipoteza zerowa jest prawdziwa. A potem spróbują udowodnić, że to nieprawda do wcześniej określonego poziomu pewności, zwanego poziomem istotności.
Ale tak Bayesian podchodzi do tego samego testu:
Zaczynają od wcześniejszego przekonania, że oba przyciski A i B mają równe szanse na uzyskanie współczynnika konwersji od 0 do 100%. Tak więc od razu jest równość przycisków — oba mają 50% szans na bycie najlepszym wykonawcą.
Następnie rozpoczyna się test i zbierane są dane. Obserwując nowe informacje, testerzy Bayesa A/B będą aktualizować swoją wiedzę. Tak więc, jeśli B jest obiecujący, mogą osiągnąć późniejsze przekonanie na podstawie tej obserwacji, mówiąc: „B ma 61% szans na pokonanie A”.
Istnieją zasadnicze różnice między tymi dwiema metodami.
Dlatego tak ważne jest dla nas zachowanie bezstronnego podejścia do Bayesowskich testów A/B.
Większość Bayesowskich narzędzi do testowania A/B — być może w celach marketingowych — przyjmuje skrajnie antyczęstotliwościowe stanowisko i przekonuje, że Bayesian jest lepszy w informowaniu, który wariant jest bardziej „opłacalny”.
Ale czy jakiekolwiek statystyczne podejście do testów A/B posiada wyłączne prawa do wglądu?
Jeśli ktoś pchnie dalej argument bayesowski, może stanąć w obliczu badań, w których respondenci twierdzą, że chcą wiedzieć, jaki jest najlepszy kierunek działania, że chcą zmaksymalizować zyski lub coś podobnego. Stawia to pytanie mocno na terytorium teorii decyzji – coś, na co ani wnioskowanie bayesowskie, ani wnioskowanie częstościowe nie mogą mieć bezpośredniego wpływu.
Georgi Georgiev, twórca Analytics-toolkit.com i autor „Metod statystycznych w testach A/B online”
W następnych sekcjach pokrótce omówimy te szczegóły. Na razie postarajmy się, aby reszta tego podkładu była łatwa do uchwycenia.
Krótki słownik terminów bayesowskich, które mają znaczenie dla testerów A/B
Wnioskowanie bayesowskie
Wnioskowanie bayesowskie aktualizuje prawdopodobieństwo hipotezy o nowe dane. Jest zbudowana wokół wierzeń i prawdopodobieństw.
Wnioskowanie bayesowskie wykorzystuje prawdopodobieństwo warunkowe, aby pomóc nam zrozumieć, w jaki sposób dane wpływają na nasze przekonania. Powiedzmy, że zaczynamy od wcześniejszego przekonania, że niebo jest czerwone. Po przyjrzeniu się niektórym danym szybko zdamy sobie sprawę, że to wcześniejsze przekonanie jest błędne. Dlatego przeprowadzamy aktualizację bayesowską, aby poprawić nasz błędny model koloru nieba, uzyskując dokładniejsze przekonanie a posteriori .
Michael Berk w W stronę nauki o danych
Warunkowe prawdopodobieństwo
Prawdopodobieństwo warunkowe to prawdopodobieństwo zdarzenia, biorąc pod uwagę, że zaszło inne zdarzenie. Oznacza to, że prawdopodobieństwo A pod warunkiem B.
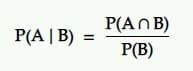
Tłumaczenie: Prawdopodobieństwo zajścia zdarzenia A przy innym zdarzeniu B jest równe prawdopodobieństwu zajścia B i A razem podzielonego przez prawdopodobieństwo zdarzenia B.
Rozkład prawdopodobieństwa/Rozkład prawdopodobieństwa
Rozkłady prawdopodobieństwa to rozkłady, które pokazują, jak prawdopodobne jest, że Twoje dane przyjmą określoną wartość.
Tam, gdzie dane mogą przyjmować wiele wartości, na przykład kategorię taką jak kolory, które mogą być szare, czerwone, pomarańczowe, niebieskie itp., rozkład jest wielomianowy. Dla zestawu liczb rozkład może być normalny. A dla wartości danych, które mogą być tak/nie lub prawda/fałsz, będzie to dwumian.
Uprzednia dystrybucja przekonań
Lub wcześniejszy rozkład prawdopodobieństwa, zwany po prostu uprzednim, wyraża twoje przekonanie, zanim uzyskasz dowody na nowe dane. Jest to więc wyraz twojego początkowego przekonania, które zamierzasz zaktualizować po rozważeniu pewnych dowodów za pomocą analizy Bayesowskiej (lub wnioskowania).
Koniugacja
Przede wszystkim koniugat odnosi się do bycia łączonymi, zwykle w parach. W bayesowskiej teorii prawdopodobieństwa sprzężenie zakłada, że a priori jest sprzężony z prawdopodobieństwem.
Jeśli a posteriori ma taką samą formę funkcjonalną jak a priori, a priori jest sprzężona z funkcją wiarygodności. Pokazuje to, jak funkcja wiarygodności aktualizuje poprzednią dystrybucję.
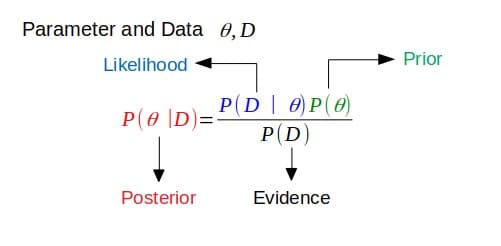
Sprzężona Przeorów
Wiąże się to z powyższą definicją. Jeśli a posteriori znajduje się w tej samej rodzinie rozkładów prawdopodobieństwa (lub ma taką samą formę funkcjonalną) jak rozkład prawdopodobieństwa a priori, to rozkład a priori i a posteriori są sprzężone. W tym przypadku a priori nazywa się sprzężoną przed funkcji prawdopodobieństwa.
Mogą być subiektywne (oparte na wiedzy eksperymentatora), obiektywne i informacyjne (oparte na danych historycznych) lub nieinformacyjne.
Funkcja straty
Funkcja straty to sposób na ilościowe określenie straty poprzez pomiar, jak złe jest nasze obecne oszacowanie. Pomaga nam zminimalizować straty związane z testowaniem hipotez, zwłaszcza przy wyrażaniu wnioskowania, które leży w zakresie prawdopodobnych wartości, oraz wspomaga podejmowanie decyzji za pomocą naszych wyników testów.
Teraz to na uboczu, możemy iść dalej.
Jeśli przez jakiś czas byłeś w okolicy, prawdopodobnie natknąłeś się na więcej niż kilka memów statystycznych Frequentist vs Bayes.

Obie strony wydają się szukać odpowiedzi z przeciwnych kierunków, ale czy tak jest naprawdę? Aby lepiej to zrozumieć (pozostawiając bezstronność), odwiedźmy obóz Frequentists.
Co to są statystyki częstych?
Jest to pierwsza technika wnioskowania, której większość ludzi uczy się w statystykach. Statystyka częsta oblicza prawdopodobieństwo, że zdarzenie (hipoteza) występuje często w tych samych warunkach.
Testowanie hipotezy A/B przy użyciu podejścia częstościowego obejmuje następujące kroki:
- Zadeklaruj kilka hipotez. Zazwyczaj hipoteza zerowa mówi, że nowy wariant „B” nie jest lepszy niż oryginalny „A”, podczas gdy hipoteza alternatywna deklaruje coś przeciwnego.
- Z góry określ wielkość próbki, korzystając ze statystycznego obliczenia mocy , chyba że korzystasz z sekwencyjnych metod testowania. Użyj kalkulatora wielkości próbki, który uwzględnia moc statystyczną, aktualny współczynnik konwersji i minimalny wykrywalny efekt.
- Uruchom test i poczekaj, aż każda odmiana zostanie wystawiona na wstępnie określoną wielkość próbki.
- Oblicz prawdopodobieństwo zaobserwowania wyniku co najmniej tak ekstremalnego jak dane przy hipotezie zerowej (wartość p). Odrzuć hipotezę zerową i zastosuj nowy wariant do produkcji, jeśli wartość p < 5%.
Jak to się ma do Bayesa? Zobaczmy…
Bayesowski vs częsty test A/B
Jest to głośna debata wszędzie tam, gdzie używa się wnioskowania statystycznego. I szczerze mówiąc, nie ma to sensu. Oba mają swoje zalety i przypadki, w których są najlepszą metodą do użycia.
W przeciwieństwie do tego, co myśli większość promotorów w obu obozach, są oni podobni pod wieloma względami i żaden nie zbliża się do prawdy niż drugi — chociaż ich podejście jest różne.
Na przykład w przypadku testów A/B żadna konkretna metoda nie zapewni absolutnej i dokładnej prognozy w zakresie przebiegu działań, które spowodują rozwój firmy. Zamiast tego testy A/B pomagają usunąć ryzyko związane z podejmowaniem decyzji.
Bez względu na to, jak analizujesz swoje dane – stosując podejście Bayesowskie lub Frequentystyczne – możesz wykonywać ruchy z pewnym poziomem pewności, że masz rację.
I z tego powodu oba modele statystyczne są prawidłowe. Bayesian może mieć przewagę szybkości, ale jest bardziej wymagający obliczeniowo niż Frequentist.
Sprawdź inne różnice…
Ramy Frequentystyczne
Większość z nas zna częstościowe podejście z kursów wprowadzających do statystyki. Zdefiniowaliśmy powyższą metodologię — od zadeklarowania hipotezy zerowej, określenia wielkości próby, zebrania danych za pomocą randomizowanego eksperymentu, aż po obserwację statystycznie istotnego wyniku.
W Frequentism postrzegamy prawdopodobieństwo jako fundamentalnie związane z częstotliwością powtarzających się zdarzeń. Tak więc, w uczciwym rzucie monetą, Frequentysta wierzy, że jeśli będzie zgadywał wystarczająco często, to w 50% przypadków trafi poprawnie orłem i to samo w przypadku reszki.
Nastawienie częsty: „Jeśli powtarzam eksperyment w tych samych warunkach w kółko, jakie są szanse, że moja metoda otrzyma właściwą odpowiedź?”
Ramy Bayesowskie
Podczas gdy podejście częstościowe traktuje parametr populacji dla każdego wariantu jako (nieznaną) stałą, podejście bayesowskie modeluje każdą wartość parametru jako zmienną losową z pewnym rozkładem prawdopodobieństwa.
Tutaj obliczasz rozkłady prawdopodobieństwa (a tym samym wartości oczekiwane) bezpośrednio dla interesujących Cię parametrów.
Aby modelować rozkład prawdopodobieństwa dla każdego wariantu, opieramy się na regule Bayesa, aby połączyć wyniki eksperymentu z wszelką posiadaną wcześniej wiedzą na temat interesującej nas metryki. Obliczenia można uprościć, używając sprzężonego wcześniej.
Alex Birkett podsumował algorytm bayesowski w ten sposób:
- Zdefiniuj wcześniejszy rozkład, który zawiera Twoje subiektywne przekonania na temat parametru. Przeor może być nieinformacyjny lub informacyjny.
- Zbierać dane.
- Zaktualizuj swój poprzedni rozkład danymi przy użyciu twierdzenia Bayesa (chociaż możesz mieć metody bayesowskie bez wyraźnego użycia reguły Bayesa — patrz nieparametryczny bayesowski), aby uzyskać rozkład a posteriori. Rozkład a posteriori to rozkład prawdopodobieństwa, który reprezentuje zaktualizowane przekonania na temat parametru po obejrzeniu danych.
- Przeanalizuj rozkład a posteriori i podsumuj go (średnia, mediana, odchylenie standardowe, kwantyle…).
Krótko mówiąc, eksperymentator bayesowski skupia się na własnej perspektywie i na tym, czym jest dla nich prawdopodobieństwo. Ich opinia ewoluuje wraz z zaobserwowanymi danymi. Z drugiej strony częstowcy uważają, że gdzieś tam jest właściwa odpowiedź.

Zrozum, że debata Frequentist vs Bayesowska nie wpływa aż tak bardzo na analizę po testach A/B. Główne różnice między tymi dwoma obozami są bardziej związane z tym, co można przetestować.
Statystyki prawdopodobieństwa nie są na ogół wykorzystywane w dalszej analizie w dużym stopniu. Argument bayesowski i częsty jest bardziej odpowiedni w przypadku wyboru zmiennych, które mają być testowane w paradygmacie A/B, ale nawet tam większość testerów A/B piekielnie łamie hipotezy badawcze, prawdopodobieństwo i przedziały ufności .
Dr Rob Balon do CXL
Georgi dalej rozwija:
Istnieje wiele internetowych kalkulatorów bayesowskich i co najmniej jeden główny dostawca oprogramowania do testów A/B, który stosuje silnik statystyczny bayesowski, który używa tak zwanych nieinformacyjnych a priori (trochę mylące, ale nie zagłębiajmy się w to). W większości przypadków wyniki z tych narzędzi pokrywają się liczbowo z wynikami testu częstych na tych samych danych. Powiedzmy, że narzędzie bayesowskie zgłosi coś w rodzaju „96% prawdopodobieństwa, że B jest lepsze niż A”, podczas gdy narzędzie częstotliwościowe wygeneruje wartość p równą 0,04, co odpowiada 96% poziomowi ufności.
W sytuacji takiej jak powyższa, która jest znacznie bardziej powszechna niż niektórzy chcieliby przyznać, obie metody doprowadzą do tego samego wnioskowania, a poziom niepewności będzie taki sam, nawet jeśli interpretacja będzie inna.
Co powiedziałby Bayesianin o tym wyniku? Czy zmienia wartość p w odpowiednie prawdopodobieństwo a posteriori podczas oglądania scenariusza, w którym nie ma wcześniejszych informacji? A może wszystkie te zastosowania testów bayesowskich są błędne, jeśli chodzi o używanie nieinformacyjnego przekładu per se?
Naprawdę nie ma potrzeby wybierania obozu i szukania miejsca za osłoną, aby rzucać kamieniami w drugi obóz. Istnieją nawet dowody na to, że obie struktury dają takie same wyniki. Bez względu na to, którą drogę wybierzesz, miejsce docelowe prawdopodobnie będzie takie samo. To zależy od tego, jak możesz się tam dostać z Frequentist vs Bayesian.
Na przykład:
- Istnieją dane, które pokazują, że testowanie bayesowskie jest szybsze i jest preferowanym wyborem dla interaktywnych eksperymentów:
Ponieważ paradygmat bayesowski pozwala eksperymentatorom na formalną kwantyfikację przekonań i włączenie dodatkowej wiedzy, jest szybszy niż tradycyjna analiza statystyczna.
W Bayesowskiej symulacji testów A/B, gdy skorygowano kryterium decyzyjne (tj. zwiększenie tolerancji na błędy), 75% eksperymentów zakończyło się w zakresie 22,7% obserwacji wymaganych przez tradycyjne podejście (przy 5% poziomie istotności). I zanotował tylko 10% błędu typu II. - Bayesian jest również uważany za bardziej wyrozumiały, podczas gdy Frequentist unika ryzyka:
Podczas gdy wiele testów częstych wykorzystuje istotność statystyczną 95%, Bayesowie mogą być zadowoleni z mniejszej wartości. Jeśli wariant ma 78% szans na pokonanie kontroli, w zależności od oczekiwanej straty, słuszną decyzją może być wdrożenie tego wariantu.
Jeśli się mylisz, a oczekiwana strata jest mniejsza niż jeden procent, dla wielu firm jest to dość nieznaczna szkoda. To nieostrożne podejście może być lepiej dostosowane do szybkiego podejmowania decyzji w scenariuszach o bardzo niskim ryzyku. - Jednak symulacje i obliczenia bayesowskie są trudne do obliczeń:
Frequentystka natomiast pracuje na papierze i długopisie. Zastrzeżenie: Jeśli Twoje narzędzie do testowania A/B używa Bayesa i nie wiesz, jakie założenia są dodawane do Twoich danych, nie możesz polegać na „odpowiedzi” udzielonej przez dostawcę. Weź to ze szczyptą soli. I przeprowadź własną analizę.
Bayesian to nie tylko słońce i tęcze. Jak wskazuje Georgi z tą listą pytań:
- „Czy chcesz otrzymać iloczyn prawdopodobieństwa a priori i funkcji prawdopodobieństwa?”
- „Czy chcesz połączyć wcześniejsze prawdopodobieństwa i dane jako dane wyjściowe?”
- „Czy chcesz, aby subiektywne przekonania zmieszane z danymi dały wynik?” (jeśli używasz informacyjnych priorów)
- „Czy czułbyś się komfortowo prezentując statystyki, w których istnieją wcześniejsze informacje, które, jak się zakłada, są wysoce pewne, zmieszane z rzeczywistymi danymi?”
To są wszystkie aspekty statystyki bayesowskiej, używając terminologii laika.
Co właściwie mówią statystyki Bayesa w testach A/B?
Zaprojektowałeś swój test A/B, aby dać wgląd w to, jak zmiana wpływa na Twoje zainteresowania, takie jak współczynnik konwersji lub przychód na odwiedzającego.
Kiedy używasz narzędzia, które współpracuje ze statystykami Bayesa, ważne jest, aby zrozumieć, co oznaczają Twoje wyniki, ponieważ „B jest zwycięzcą” nie oznacza dokładnie tego, co większość ludzi myśli, że to robi.
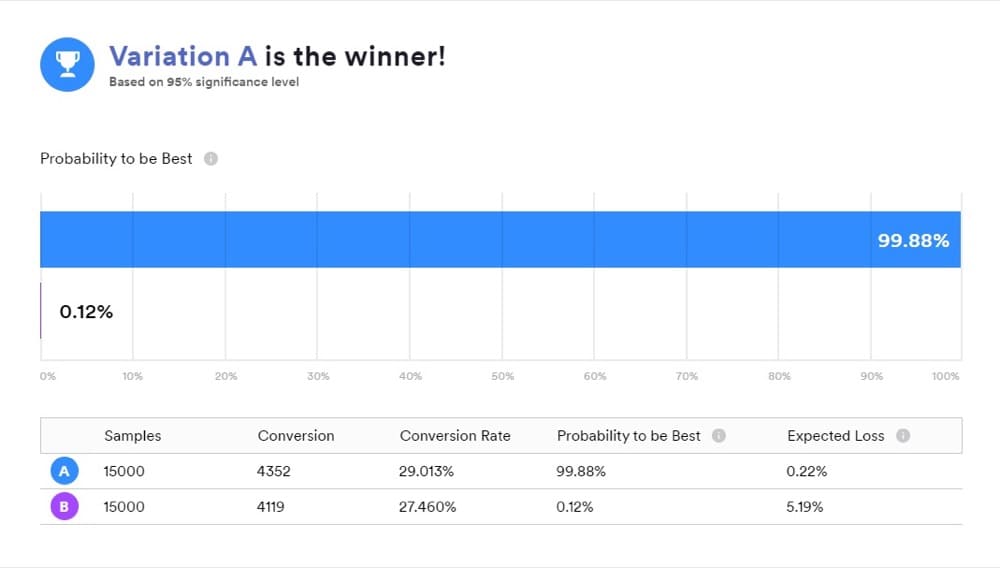
To wygodny sposób prezentowania wyników, ale nie to ujawnił Twój test. Zamiast tego odpowiedzi, których potrzebujesz, znajdują się w późniejszym porównaniu „A” i „B”.
Oto 3 metody porównania:
Prawdopodobieństwo bycia najlepszym (P2BB)
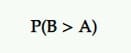
Jest to prawdopodobieństwo, które ogłasza zwycięzcę w Bayesowskich testach A/B.
Wariant z prawdopodobieństwem, że będzie najlepszy, to ten z największym prawdopodobieństwem dalszego przewyższania drugiego.
Jest to obliczane na podstawie zestawu próbek a posteriori miary będącej przedmiotem zainteresowania z oryginału i prowokatora.
Tak więc, jeśli na przykład B ma największe prawdopodobieństwo zwiększenia współczynników konwersji, B zostaje ogłoszony zwycięzcą.
Oczekiwany wzrost
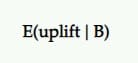
Więc jeśli B jest zwycięzcą, jak dużego wzrostu powinniśmy się po nim spodziewać? Czy nadal przyniesie te same wyniki, które widzieliśmy w teście?
To jest wgląd, który ma zapewnić oczekiwany wzrost. Oczekiwany wzrost przy wyborze B nad A, przy danym zestawie próbek a posteriori, jest definiowany jako wiarygodny przedział (lub średnia) wzrostu procentowego.
W testach A/B zwykle porównujemy to jako rywala z kontrolą. Tak więc, jeśli pretendent przegrał, jest to przedstawiane w wartościach ujemnych (np. -11,35%) i dodatnich (np. +9,58%), jeśli wygra.
Oczekiwana strata
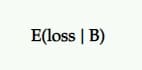
Ponieważ nie ma 100% prawdopodobieństwa, że B jest lepsze niż A, istnieje szansa na odnotowanie straty, jeśli wybierzesz B zamiast A. Jest to przedstawiane jako oczekiwana strata i, podobnie jak w przypadku oczekiwanego wzrostu, jest wyrażona na podstawie punktu widzenia pretendenta wobec kontroli.
Informuje o ryzyku wyboru wariantu P2BB (tj. ogłoszonego zwycięzcy).
Zanim zagłębimy się w mity, wielkie podziękowania dla legendy analityków Georgi Georgieva. Jego dogłębne analizy wnioskowania częstościowego i bayesowskiego oraz prawdopodobieństwa bayesowskiego i statystyk w testach A/B zainspirowały następną sekcję.
Mity dotyczące statystyk Bayesa, których należy unikać
Dzięki rywalizacji, która jest prawie tak stara, jak niepotrzebna, debata Bayesa vs Frequentystyczna zebrała wiele wkładu – i dała początek wielu mitom.
Największy z tych mitów (mit 2) jest promowany przez dostawców narzędzi do testowania A/B, aby wyjaśnić, dlaczego jedno podejście jest lepsze od drugiego.
Ale po przeczytaniu powyższych sekcji wiesz lepiej.
Odkryjmy dziury w tych mitach.
Mit nr 1: Bayesowie wyrażają swoje założenia, częstowcy nie
Sugeruje to, że bayesowie przyjmują założenia w postaci wcześniejszych rozkładów i są one otwarte do oceny. Ale Frequentyści przyjmują założenia, które są ukryte w środku matematyki.
Dlaczego to jest złe: Bayesianie i Frequentyści przyjmują podobne podstawowe założenia, jedyną różnicą jest to, że Bayesianie przyjmują dodatkowe założenia — oprócz matematyki.
Modele Frequentystyczne wykorzystują założenia matematyczne, takie jak kształt rozkładu, jednorodność lub niejednorodność efektu w ramach obserwacji oraz niezależność obserwacji. I nie są ukryte. W rzeczywistości są one szeroko omawiane w społeczności statystycznej i podawane dla każdego testu statystycznego częstości.
Prawda: Frequentyści wyraźnie określają swoje założenia i idą o krok dalej, aby przetestować założenia: testy na normalność, test dobroci dopasowania (w ramach którego mamy test niedopasowania proporcji próby) i inne.
Mit 2. Metody Bayesowskie dają odpowiedzi, których naprawdę potrzebujesz
Błędne założenie polega na tym, że wartości p i przedziały ufności nie mówią testerom tego, co chcą wiedzieć, podczas gdy prawdopodobieństwo a posteriori i przedziały wiarygodności tak. Ludzie chcą wiedzieć takie rzeczy jak
- Prawdopodobieństwo, że B przewyższa A i
- Prawdopodobieństwo, że wynik nie jest zbiegiem okoliczności.
Testy wartości P i hipotez (wnioskowanie proste) nie dostarczają tych informacji, ale wnioskowanie odwrotne tak.
Dlaczego jest źle: To kwestia językoznawcza. Ogólnie rzecz biorąc, gdy niestatystycy używają terminów takich jak „prawdopodobieństwo”, „szansa” i „prawdopodobieństwo”, nie używają ich z myślą o ich technicznym znaczeniu. Sonda głębiej, a przekonasz się, że są oni tak samo zdezorientowani wnioskowaniem odwrotnym, jak wnioskowaniem prostym.
Według Georgi Georgieva zaczynają się pojawiać takie pytania:
- “ Jakie jest prawdopodobieństwo a priori? Jaką to ma wartość?”
- „Co to jest funkcja wiarygodności?”
- „Jakie „wcześniejsze” prawdopodobieństwo, nie mam wcześniejszych danych?”
- „Jak mam bronić wyboru prawdopodobieństwa a priori?”
- „Czy istnieje sposób na przekazanie tego, co mówią dane, bez żadnej z tych mieszanin?”
Prawda: Powinien być lepszy wgląd w to, co testerzy chcą wiedzieć, a nie w ich błędną interpretację terminów technicznych. Wartości P, przedziały ufności i inne informują o tym, jak dobrze sprawdzane są wyniki na podstawie zebranych danych. Stanowiły miarę pewności bez wpływu subiektywnych, niesprawdzonych wcześniejszych założeń.
Mit 3: Wnioskowanie bayesowskie pomaga komunikować niepewność lepiej niż wnioskowanie częsty
Ponieważ wyniki testów dają więcej „istotnych” spostrzeżeń.
Dlaczego to jest złe: Zarówno metody częsty, jak i bayesowskie mają podobne narzędzia, które pomagają w komunikowaniu pewności i wyników testu A/B.
| Frequentysta | Bayesian | ||||||||||
| ● Szacunki punktowe | ● Szacunki punktowe | ||||||||||
| ● Wartości P | ● Wiarygodne interwały | ||||||||||
| ● Przedziały ufności | ● Czynniki Bayesa | ||||||||||
| ● Krzywe wartości P | ● Rozkłady tylne (wykonaj to samo zadanie jako krzywe Frequentist) | ||||||||||
| ● Krzywe ufności | |||||||||||
| ● Krzywe dotkliwości itp. |
Prawda: wszystko zależy od tego, jak ich używasz. Obie metody są równie skuteczne w komunikowaniu niepewności. Istnieją jednak różnice w sposobie przedstawiania miary niepewności.
Mit 4. Wyniki testów Bayesa A/B są odporne na podglądanie
Niektórzy statystycy Bayesa twierdzą, że „test Bayesa można przerwać, gdy zobaczysz „wyraźnego zwycięzcę” i nie ma to większego wpływu na ostateczny wynik.
Zapewne wiesz, że jest to nie do zaakceptowania w testach częstych, więc jest to traktowane jako wada w porównaniu do Bayesa. Ale czy to naprawdę?
Dlaczego jest źle: W badaniu z 1969 roku opublikowanym w Journal of the Royal Statistical Society zatytułowanym „Powtarzane testy istotności akumulacji danych”, Armitage i in. pokazali, w jaki sposób opcjonalne zatrzymanie oparte na wynikach zwiększa prawdopodobieństwo błędu.
Nie możesz po prostu przestać, gdy zauważysz zwycięzcę, zaktualizuj swój a posteriori i użyj go jako następnego poprzedniego bez zmiany sposobu działania analizy bayesowskiej.
Prawda: podglądanie wpływa na wnioskowanie bayesowskie tak samo jak częsty (jeśli chcesz zrobić to dobrze).
Mit nr 5 Statystyki Frequentist są nieefektywne, ponieważ trzeba czekać na ustaloną wielkość próbki
Niektórzy członkowie społeczności CRO uważają, że częste testy statystyczne muszą być przeprowadzane na stałej, z góry określonej wielkości próby, w przeciwnym razie wyniki są nieważne.
W rezultacie czekasz dłużej niż to konieczne, aby uzyskać pożądane rezultaty.
Dlaczego to jest złe: statystyki częstych nie są używane w ten sposób od około siedmiu dekad. W przypadku często wykonywanych testów sekwencyjnych nie jest wymagany ustalony z góry czas trwania.
Prawda: testy sekwencyjne, które są dziś bardziej popularne, wymagają maksymalnej wielkości próby, aby zrównoważyć błędy typu I i typu II, ale rzeczywista wielkość użytej próby różni się w zależności od przypadku w zależności od obserwowanego wyniku.
Więc, czy powinieneś wybrać Bayesa czy Frequentistę? Jest miejsce dla obu.
Nie trzeba wybierać strony. Obie metody mają swoje miejsce. Na przykład, długoterminowy projekt, który wykorzystuje zaktualizowane założenia wstępne i potrzebuje szybkich wyników, lepiej prezentuje się z podejściem bayesowskim.
Natomiast metoda Frequentystyczna najlepiej sprawdza się w projektach, które wymagają znacznej powtarzalności wyników. Na przykład w pisaniu oprogramowania, z którego będzie korzystać wiele osób z wieloma zestawami danych.
Jak mówi Cassie Kozyrkov, szef działu Decision Intelligence w Google: „Statystyka to nauka o zmianie zdania w sytuacji niepewności”.
W swoim podsumowaniu Bayesian vs Frequentist Statistics powiedziała:
„Możesz wziąć tę debatę frequentystyczną i bayesowską i sprowadzić ją do tego, o czym zmieniasz zdanie. Frequentyści zmieniają zdanie na temat działań, mają preferowane działanie domyślne — może nie mają żadnych przekonań — ale mają działanie, które lubią pod ignorancją, a następnie pytają: „Czy moje dowody [lub dane] zmieniają zdanie na temat to działanie?” „Czy czuję się śmiesznie, robiąc to w oparciu o moje dowody?”
Z drugiej strony Bayesowie zmieniają zdanie w inny sposób. Zaczynają od opinii, matematycznie wyrażonej osobistej opinii, zwanej przeorem, a następnie pytają: „Jaką rozsądną opinię powinienem mieć po włączeniu pewnych dowodów?” I tak Frequentyści zmieniają zdanie na temat działań, Bayesianie zmieniają zdanie na temat przekonań.
I w zależności od tego, jak chcesz ułożyć proces podejmowania decyzji, możesz preferować jeden obóz zamiast drugiego”.
W końcu wszyscy zmierzamy do podobnych wniosków — różnica polega na tym, jak te wnioski są przedstawiane Tobie.
Gdyby wnioskowanie częstościowe i bayesowskie były funkcjami programistycznymi, w których dane wejściowe byłyby problemami statystycznymi, to te dwie rzeczy różniłyby się tym, co zwracają użytkownikowi. Funkcja wnioskowania z częstością zwracałaby liczbę reprezentującą oszacowanie (zazwyczaj statystykę podsumowującą, taką jak średnia próbki itp.), podczas gdy funkcja bayesowska zwróciłaby prawdopodobieństwa.
Fragment książki „Programowanie probabilistyczne i metody bayesowskie dla hakerów”
Niezupełnie słuszne jest twierdzenie, że jedno daje bardziej praktyczne wyniki niż drugie.
Zabrany klucz
Statystyki bayesowskie w testach A/B składają się z 4 odrębnych kroków:
- Zidentyfikuj swoją poprzednią dystrybucję
- Wybierz model statystyczny, który odzwierciedla Twoje przekonania
- Uruchom eksperyment
- Wykorzystaj wyniki, aby zaktualizować swoje przekonania i obliczyć rozkład a posteriori
Twoje wyniki wskażą Ci wnikliwe prawdopodobieństwa. Dzięki temu będziesz wiedzieć, który wariant ma największe prawdopodobieństwo, że będzie najlepszy, Twoją oczekiwaną stratę i oczekiwany wzrost.
Są one zwykle interpretowane przez większość narzędzi do testowania A/B przy użyciu statystyk Bayesa. Ale dokładny eksperymentator wykona analizę po testach, aby lepiej zrozumieć te wyniki.
Ponieważ dotarłeś tak daleko, oto ciekawostka dla Ciebie: znasz portret Thomasa Bayesa, który wszyscy znają? Ten:

Nikt nie jest w 100% pewien, że to on.