프로그래밍 감각으로 미적분학 느끼기

저는 코딩을 할 수 있는 사람들이 미적분학보다 더 복잡한 개념을 이해할 수 있는 능력을 가지고 있다고 믿습니다. 여전히 미적분학으로 어려움을 겪고 있는 재능 있는 프로그래머가 많은 이유 중 하나는 그것이 어렵기 때문이 아닙니다. 그것은 대부분 우리가 (다른 많은 주제들과 함께) 잘못된 방식으로 그것을 배웠기 때문입니다.

인생에서 코딩을 해본 적이 있다면, 심지어 소수 생성과 같은 장난감 연습을 하더라도 미적분학에서 일어나는 유사한 일을 이미 했을 수 있지만 관련시킬 기회는 없었을 것입니다.

이 글의 목적은 미적분학이나 프로그래밍을 가르치는 것이 아니라 몇 가지 점을 연결하는 데 도움이 되는 것입니다.

잠시 후 코딩 부분으로 이동하겠습니다. 하지만 그 전에 간단한 배경 정보를 제공하겠습니다.

변화율

미적분학은 "변화율"에 대해 이야기합니다. 그것이 무엇을 의미하는지 이해하려고 노력합시다.

변수(x)의 변화에 ​​대해 함수의 변화율은 단순히 함수의 변화를 x의 변화로 나눈 것입니다. 실제 숫자로 시각화하자:

2개의 점 x=2 및 x=6과 함수 y=f(x) = x²를 고려하십시오.

또한 dx = x축에서 이 두 점 사이의 거리를 고려하십시오. 그리고 dy 는 이러한 x 값에 대한 y 값 사이의 거리입니다.

그러면 x=2에서 x=6으로의 y 변화율은 다음과 같습니다.

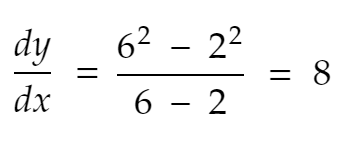
유도체

이제 — 도함수 dy/dx는 x의 극히 작은 변화에 대한 y의 변화율입니다. 이 거리(6–2=4)는 극도로 작지 않고 가깝지도 않기 때문에 위의 방정식을 도함수라고 부를 수 없습니다. 이제 더 작은 숫자 0.1을 선택하겠습니다.

x = 0일 때 y = x² = 0² = 0입니다.

양의 방향에 가장 가까운 이웃, x = 0.1. 거기에서 y는 0.1² = 0.01이 됩니다.

그래서,

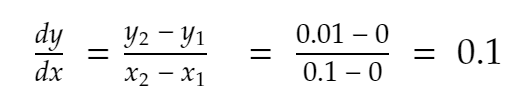
한 번 더 시도해 보겠습니다. 양의 방향에 대한 0.1의 가장 가까운 이웃, x = 0.2. 따라서 y는 0.2² = 0.04가 됩니다. 그래서,

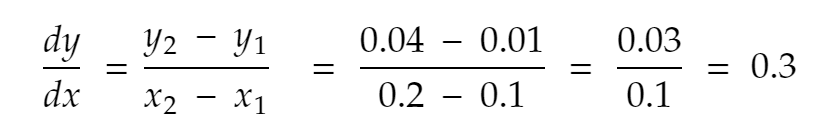
이 과정을 몇 번 더 반복하면 다음과 같이 됩니다.

가지고 놀고 싶다면 여기 엑셀 파일이 있습니다.

dx (x축에서 인접한 두 점 사이의 가상의 극미하게 작은 거리)는 우리 맥락에서 0.1입니다.

x 는 그에 따라 증가합니다.

y 는 단순히 x²입니다.

dy 는 2개의 인접한 y 값 사이의 거리입니다. 예를 들어 x= 0.1일 때 현재 y(0.01)와 다음 y(0.04) 사이의 거리는 0.03이므로 x=0.1에서 dy는 0.03입니다.

dy/dx 는 dy를 dx로 나눈 값입니다.

dy/dx / x 는 dy/dx를 x로 나눈 값입니다.

이제 x가 증가함에 따라 마지막 행이 2에 접근한다는 것을 알 수 있습니다. 즉, x에 대한 x²의 변화율은 x의 두 배인 2x 에 접근합니다.

x에 대한 x²의 도함수를 기억합니까? 2배! 연결을 찾으십니까?

코딩 시간

지금까지 논의한 내용을 코드로 시도해 보겠습니다.

Python이 이미 설치되어 있다고 가정하고 터미널에서 다음을 실행합니다.

그 후 다음 Python 코드를 실행합니다.

여기:

x : 0에서 9까지의 숫자를 포함합니다.

y : 다른 배열, 각 요소는 해당 x 요소의 제곱

dy : 0으로 초기화된 다른 배열. 우리는 이 배열에 y-거리를 넣을 것입니다.

dydx : 0으로 초기화된 또 다른 배열. 모든 포인트의 dy/dx 값을 포함합니다.

dx : 꽤 분명합니다. 스텝 크기입니다. SIZE가 증가함에 따라 감소하는 2개의 연속 숫자 사이의 거리. SIZE = 10이면 dx = 1. SIZE = 100이면 dx = 0.1입니다.

첫째, 우리는 모든 점에 대해 dy를 유도합니다. 그런 다음 여기에서 dydx를 계산합니다.

그것을주의해라:

여기서는 첫 번째 값과 마지막 값을 생략합니다. x의 첫 번째 값은 0이며, 이는 0분할 오류를 생성합니다. 그리고 dy의 마지막 값이 없기 때문에 dy/dx의 마지막 값을 계산할 수 없습니다. 왜냐하면 여기에는 없는 y의 마지막 사용 가능한 값 옆에 필요하기 때문입니다.

모든 것이 잘되면 다음 그래프가 표시됩니다.

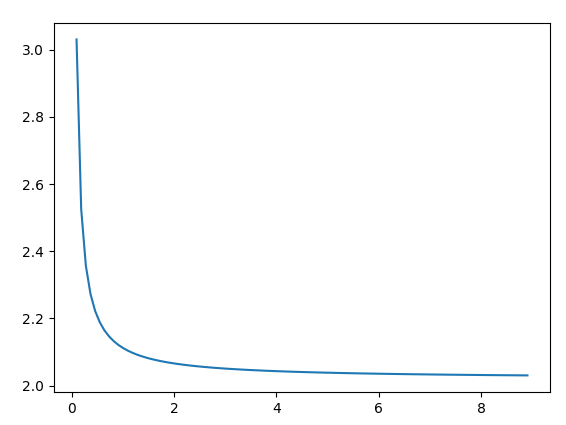
줄거리에서 이해하는 것

보시다시피 그래프가 2에 가까워지고 있습니다. SIZE 값(dx보다 낮게 설정됨)을 늘리고 그래프가 2에 더 빨리 접근하는 방법을 확인합니다.

두 번째 도함수

이제 여기까지 왔으므로 2차 도함수를 실현하기 위한 몇 가지 단계만 더 거치면 모든 차수의 도함수에 대한 직관을 얻을 수 있습니다.

기억하시겠지만, 2차 도함수는 x에 대한 1차 도함수의 변화율입니다. 간단히 말해서 — 2차 도함수의 dy/dx는 1차 도함수의 y와 같습니다.

위의 코드를 다음과 같이 수정해 봅시다.

2개의 배열을 더 선언합니다.

d2ydx2 : 2차 도함수를 나타냅니다.

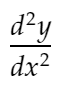
distance_dydx: 인접한 두 점 사이의 dy/dx 값 사이의 거리를 나타냅니다.

다음은 2차 도함수의 전체 코드입니다.

for 루프에서 dydx를 계산한 후 다른 루프를 실행하여 2차 도함수를 계산합니다. 약간의 현명한 코딩을 통해 동일한 루프에서 2차 도함수를 계산할 수 있습니다(연습으로 시도). 하지만 명확성을 위해 여기에서 분리했습니다.

또한 다음 사항에 유의하십시오.

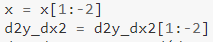
1차 도함수에서 했던 것처럼 여기에서도 일부 값을 생략합니다. 마지막 2개 값은 마지막에서 두 번째 값이 마지막 "1차 도함수" 값을 필요로 하기 때문에 생략됩니다. 이 값은 계산할 수 없습니다(위에서 설명한 대로 필요한 y 값이 없었기 때문에). 3차 도함수의 경우 마지막 3개 값을 생략해야 한다는 뜻인가요?🤔 — 그건 여러분이 찾아야 합니다.

출력 그래프는 다음과 같습니다.

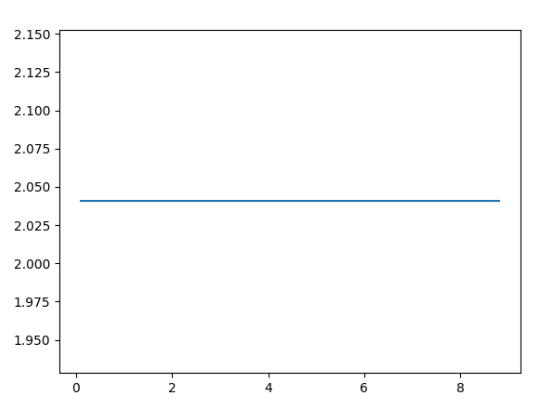
여기서 무엇을 볼 수 있습니까?

고등학교에서 알다시피:

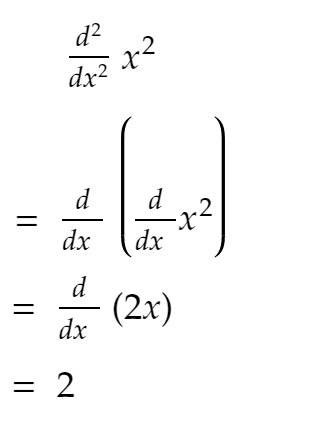
이제 위의 코드에서 볼 수 있듯이 2차 도함수는 대부분 일정하게 유지되며 SIZE를 계속 늘리면 2에 가까워집니다!

변화율이 중요한 이유

다음과 같은 사항이 궁금할 수 있습니다.

— 왜 우리는 이 모든 불쾌한 문제를 겪고 있습니까? 변화율이나 파생상품에서 어떤 유용한 정보를 얻을 수 있습니까?

— 왜 우리는 어떤 금액에도 변화율을 적용할 수 없습니까? 왜 극도로 작습니까? 더 큰 값에 대한 변화율에서 찾을 수 없는 극미하게 작은 변화율에서 어떤 정보를 얻을 수 있습니까?

— 이 무한히 작은 것이 일종의 해킹처럼 보입니까? 우리는 정상 이상의 작은 숫자로 작업했지만 실제로는 실제로 극도로 작지는 않습니다.

내가 계속 진행하도록 허용한다면 이 기사의 길이를 보고 물러날 것이고 여기까지 오지 않았을 것입니다. 언젠가 우리가 그 질문들을 다룰 것입니다 😀.