プログラミング感覚で微積分を感じる

コーディングできる人は、微積分よりも複雑な概念を理解する能力があると思います。 まだ微積分に苦労している才能のあるプログラマーがたくさんいる理由の1つは、それが難しいということではありません。 それは主に、（他の多くのトピックとともに）間違った方法で教えられたためです。

人生でコーディングを行ったことがあれば、素数を生成するようなおもちゃのエクササイズでさえ、微積分で起こる同様のことをすでに行ったことがあるかもしれませんが、関連付ける機会はありませんでした。

この文章の目的は、微積分やプログラミングを教えることではなく、いくつかの点をつなぐ手助けをすることです。

すぐにコーディングの部分に行きます。 ただし、その前に簡単な背景を説明させてください。

変化率

微分学は「変化率」について話します。 それが何を意味するのかを理解してみましょう。

変数（x）の変化の場合、関数の変化率は、単に関数の変化をxの変化で割ったものです。 実際の数字で視覚化しましょう：

2点x=2およびx=6、および関数y = f（x）=x²を考えます。

また、 dx =x軸のこれら2点間の距離を考慮してください。 また、 dyは、これらのx値のy値間の距離です。

次に、yのx=2からx=6への変化率は次のようになります。

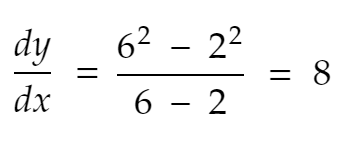
デリバティブ

現在—微分dy / dxは、xのごくわずかな変化に対するyの変化率です。 この距離（6–2 = 4）は無限小ではなく、近くでもないため、上記の方程式を導関数と呼ぶことはできません。 それで、今のところ、より小さな数、 0.1を選びましょう。

x = 0の場合、y=x²=0²=0。

正の方向に最も近い、x=0.1。 そこでyは0.1²=0.01になります。

そう、

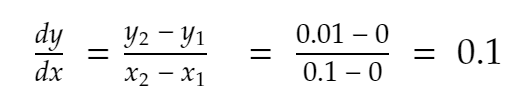
もう一度試してみましょう。 正の方向に0.1の最も近い隣、x=0.2。 したがって、yは0.2²=0.04になります。 そう、

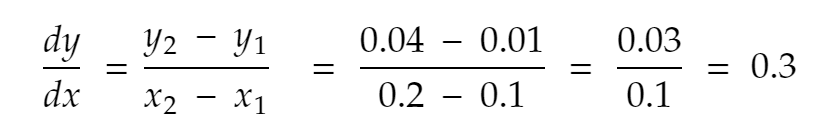
このプロセスをさらに数回繰り返すと、次のようになります。

あなたがそれで遊びたいならば、これはExcelファイルです。

dx （x軸上の2つの隣接するポイント間の架空の非常に小さい距離）は、コンテキストでは0.1です。

xはそれに応じて増加しています。

yは単にx²です。

dyは、2つの隣接するy値の間の距離です。 たとえば、x = 0.1の場合、現在のy（0.01）と次のy（0.04）の間の距離は0.03です。したがって、dyはx=0.1で0.03です。

dy / dxは、dyをdxで割ったものです。

dy / dx / xは、dy/dxをxで割ったものです。

ここで、xが増加すると、最後の行が2に近づいていることに注意してください。つまり、xに対するx²の変化率はxの2倍、つまり2xに近づいています。

xに関するx²の導関数を覚えていますか？ 2倍！ いくつかの接続を見つけますか？

コーディング時間

これまで議論してきたコードのことを試してみましょう。

すでにPythonがインストールされていると仮定して、ターミナルで次のコマンドを実行します。

その後、次のPythonコードを実行します。

ここ：

x ：0から9までの数字を含みます。

y ：別の配列、各要素は対応するx要素の正方形です

dy ：ゼロで初期化された別の配列。 この配列にy距離を入れます。

dydx ：ゼロで初期化された別の配列。 すべてのポイントのdy/dx値が含まれます。

dx ：かなり明白です—それはステップサイズです。 2つの連続する数値間の距離。これは、SIZEが増加するにつれて減少します。 SIZE = 10の場合、dx=1。SIZE=100の場合、dx=0.1。

まず、すべての点でdyを導き出します。 次に、それからdydxを計算します。

次のことに注意してください。

ここでは、最初と最後の値を省略しています。 xの最初の値は0であり、これはゼロ除算エラーを生成します。 また、dyの最後の値がないため、dy / dxの最後の値を計算することはできません。これは、ここにないyの最後の使用可能な値の隣に必要になるためです。

すべてがうまくいけば、次のグラフが表示されます。

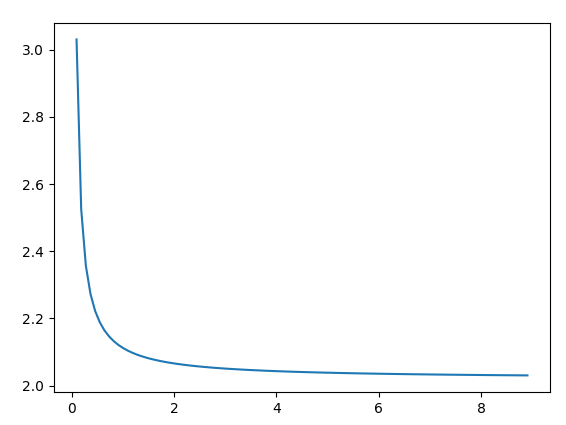
プロットから理解できること

ご覧のとおり、グラフは2に近づいています。SIZEの値を大きくして（dxを低く設定することを意味します）、グラフが2に近づく様子を確認してください。

二階導関数

ここまで来たので、二次導関数を実現するためのもう少しのステップがあります。これにより、任意の順序の導関数の直感が得られます。

ご存知のように、二次導関数はxに関する一次導関数の変化率です。 簡単に言えば、2次導関数のdy / dxは、1次導関数のyに似ています。

上記のコードに次の変更を加えましょう。

さらに2つの配列を宣言します。

d2ydx2 ：これは2階導関数を表します：

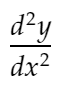
distance_dydx： 2つの隣接するポイント間のdy/dx値間の距離を表します

二次導関数の完全なコードは次のとおりです。

forループでdydxを計算した後、別のループを実行して2次導関数を計算します。 いくつかの賢明なコーディングを使用すると、同じループで2階導関数を計算できます（演習として試してください）。ただし、わかりやすくするために、ここではそれらを別々に保持しました。

また、次の点にも注意してください。

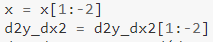
一次導関数で行ったように、ここでもいくつかの値を省略しています。 最後から2番目の値は、計算できなかった最後の「一次導関数」値を必要とするため、最後の2つの値は省略されます（上記のように、必要なy値がなかったため）。 三階導関数の場合、最後の3つの値を省略しなければならないということですか？🤔—それはあなたが見つけるためのものです。

出力グラフは次のとおりです。

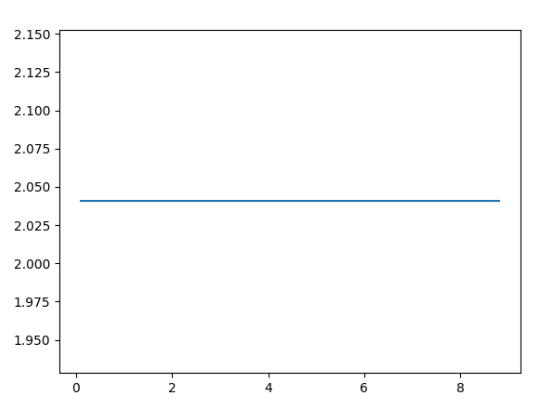
ここに何が見えますか？

あなたが高校から知っているように：

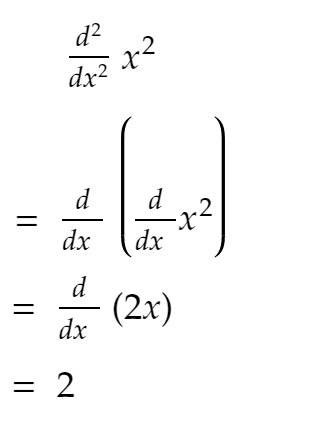
さて、上のコードからわかるように、二次導関数はほとんど一定のままであり、SIZEを増やし続けると、2に近づきます。

変化率が重要な理由

あなたは疑問に思うかもしれません：

—なぜ私たちはこれらすべての厄介な問題を乗り越えるのですか？ 変化率または導関数からどのような有用な情報が得られますか？

—なぜ、どのくらいの量の変化率でも行けないのですか？ なぜ非常に小さいのですか？ 非常に小さい場合の変化率からどのような情報が得られますか。これは、大きい値に関する変化率からは見つけることができません。

—この非常に小さなものは、ハックのように見えますか？ 私たちは大丈夫以上のいくつかの小さな数で作業しましたが、実際には非常に小さいわけではありません。

私が続けることを許せば、あなたはこの記事の長さを見て立ち去り、ここまで来なかっただろう。 たぶん、私たちはそれらの質問にいつか対処するでしょう😀。