ベイズ統計:A/Bテスターの迅速で誇大広告のない入門書
公開: 2022-06-23
A / Bテストツールによって提供された結果を解釈する能力にどの程度自信がありますか?
たとえば、ベイズ統計に基づいて構築されたツールを使用していて、「B」が「A」を破る可能性が70%であるため、「B」が勝者であると表示されます。 それが何を意味し、それがあなたのCRO戦略にどのように情報を与えるべきか知っていますか?
この記事では、A/Bテストの制御を取り戻すのに役立つベイズ統計の基礎を学びます。
- ベイズ統計の偏りのない見方
- 頻度主義とベイズの長所と短所
- いくつかの一般的な神話の罠を避けながら、ベイジアンA/Bテストの結果を自信を持って解釈して使用するために必要な準備。
- ベイズ統計とは何ですか?
- ベイジアンオリジンストーリー
- A/Bテストに適用されるベイズ統計の例
- A/Bテスターにとって重要なベイジアン用語の短い用語集
- ベイズ推定
- 条件付き確率
- 確率分布/尤度分布
- 事前信念分布
- 共役
- 共役事前分布
- 損失関数
- 頻度主義統計とは何ですか?
- ベイジアンvs頻度主義A/Bテスト
- 頻度主義フレームワーク
- ベイジアンフレームワーク
- ベイズ統計は、A / Bテストで実際に何を教えてくれますか?
- 最高になる確率(P2BB)
- 予想される上昇
- 期待損失
- 避けるべきベイズ統計に関する神話
- 神話#1:ベイジアンは彼らの仮定を述べます、頻度主義者はしません
- 神話#2。 ベイジアン法はあなたが実際に望む答えをあなたに与える
- 神話#3:ベイジアン推論は頻度主義的推論よりも不確実性を伝えるのに役立ちます
- 神話#4。 ベイジアンA/Bテストの結果は覗き見に耐性があります
- 神話#5。 固定サンプルサイズを待たなければならないため、頻度主義統計は非効率的です
- それで、あなたはベイジアンまたは頻度主義者を選ぶべきですか? 両方のための場所があります。
- 重要なポイント
準備? 基本から始めましょう。
ベイズ統計とは何ですか?
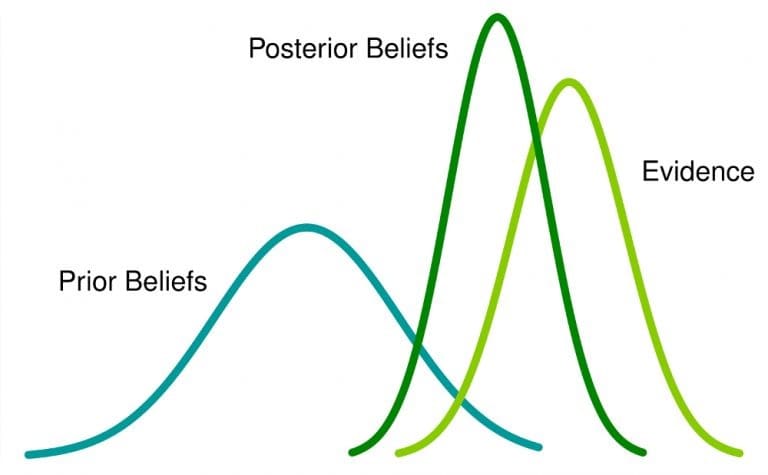
ベイズ統計は、ベイズの定理に基づく統計分析へのアプローチであり、新しいデータまたはそれらのイベントに関する証拠が収集されると、イベントに関する信念を更新します。 ここで、確率はイベントが発生するという信念の尺度です。
これが意味すること:あなたがイベントについて以前の信念を持っていて、それに関連するより多くの情報を得るならば、その信念は事後の信念に変わります(または少なくとも調整されます)。
これは、不確実性を理解する場合や、eコマースのコンバージョン率の最適化や機械学習など、ノイズの多いデータを大量に処理する場合に役立ちます。
これを想像してみましょう:
たとえば、大学の食料品のカートレースを見ていると、興奮した観客が、緑のシャツを着た女性をカートに入れている赤いTシャツの男が勝つという賭けに挑戦します。 あなたはそれについて考え、黒のジャケットの男と黒のフーディの女の子が代わりに勝つだろうと反論します。

別の観客が頭上にいて、「赤いTシャツの男が4レース中最後の3レースで優勝しました」とあなたにヒントをささやきました。 あなたの賭けはどうなりますか? もうよくわかりませんよね?
黒のジャケットの男が最後にラッキーなサングラスをかけたときに勝ったことも知ったとしましょう。 そして、彼がそれを着ていなかったとき、赤いTシャツの男が勝ちました。
今日、あなたは黒いジャケットの男がそれらの眼鏡をかけているのを見ます。 あなたの信念は再び変わります。 あなたは今あなたの賭けにもっと信頼を持っていますよね? このストーリーでは、新しいデータの証拠を取得するたびに信念を更新しました。 それがベイジアンアプローチです。
ベイジアンオリジンストーリー
トーマス・ベイズ牧師が最初に彼の理論について考えたとき、彼はそれが出版に値するとは思わなかった。 それで、それは10年以上の間彼のメモに残っていました。 彼の家族がリチャード・プライスに彼のメモを読むように頼んだとき、プライスはベイズの定理の基礎を形成するメモを発見しました。
それはベイズの思考実験から始まりました。 彼は完全に平らで正方形のテーブルに背を向けて座って、アシスタントにテーブルにボールを投げさせることを考えました。
ボールはテーブルのどこにでも着地できましたが、ベイズは新しい情報で推測を更新することでどこに着地できるかを推測できると考えました。 ボールがテーブルに着地したとき、彼はアシスタントに、前のボールが着地した場所の前または後ろの左または右に着地したかどうかを教えてもらいました。
彼はそれに気づき、より多くのボールがテーブルに着地するのを聞いた。 このような追加情報を使用して、彼は各スローで推測の精度を向上させることができることを発見しました。 これにより、観察からより多くの証拠を取得するにつれて、理解を更新するというアイデアが生まれました。
データ分析へのベイズアプローチは、科学や工学などのさまざまな分野に適用されており、スポーツや法律も含まれています。
オンラインのランダム化比較試験、特にA / Bテストでは、ベイズアプローチを4つのステップで使用できます。
- 以前の分布を特定します。
- あなたの信念を反映する統計モデルを選択してください。
- 実験を実行します。
- 観察後、信念を更新し、事後分布を計算します。
ベイズアルゴリズムと呼ばれる一連のルールを使用して、信念を更新します。
A/Bテストに適用されるベイズ統計の例
ベイジアンA/Bテストの例を説明しましょう。
ShopifyストアのCTAボタンで簡単なA/Bテストを実行したと想像してください。 「A」には「カートに追加」を使用し、「B」には「バスケットに追加」を使用します。
頻度主義者がテストにアプローチする方法は次のとおりです。
2つの代替世界があります。1つはAとBに違いがないため、テストではコンバージョン率に違いは見られません。 それが帰無仮説です。 また、他の世界では違いがあるため、一方のボタンのパフォーマンスがもう一方のボタンよりも優れています。
頻度主義者は、CTAボタンに違いがない世界1に住んでいると想定します。つまり、帰無仮説が真であると想定します。 そして、彼らは、有意水準と呼ばれる事前に決定された確実性のレベルに対して、それが間違っていることを証明しようとします。
しかし、これはベイジアンが同じテストにアプローチする方法です。
それらは、ボタンAとBの両方が0〜100%のコンバージョン率を生み出す可能性が等しいという事前の信念から始まります。 つまり、ボタンの平等は門のすぐ外にあります。どちらも50%の確率でトップパフォーマーになります。
次に、テストが開始され、データが収集されます。 ベイジアンA/Bテスターは、新しい情報を観察することで、知識を更新します。 したがって、Bが約束を示している場合、「BはAを打ち負かす可能性が61%ある」という観察に基づいて、事後確率に達することができます。
2つの方法には大きな違いがあります。
そのため、ベイジアンA/Bテストに対して公平なアプローチを維持することが重要です。
ほとんどのベイジアンA/Bテストツール(おそらくマーケティング目的)は、極端な反頻度主義的スタンスを取り、ベイジアンはどのバリアントがより「収益性が高い」かを判断するのに優れているという議論を推し進めます。
しかし、A / Bテストへの単一の統計的アプローチは、洞察に対する排他的権利を所有していますか?
ベイズの議論をさらに推し進めると、回答者が最善の行動方針を知りたい、または利益を最大化するなどのことを望んでいるという研究に直面する可能性があります。 これにより、問題は決定理論の領域にしっかりと置かれます。ベイズ推定も頻度主義的推論も直接言うことはできません。
Analytics-toolkit.comの作成者であり、「オンラインA/Bテストの統計的手法」の著者であるGeorgiGeorgiev
これらの詳細については、以降のセクションで簡単に説明します。 とりあえず、この入門書の残りの部分をわかりやすくしましょう。
A/Bテスターにとって重要なベイジアン用語の短い用語集
ベイズ推定
ベイズ推定は、仮説の確率を新しいデータで更新しています。 それは信念と確率を中心に構築されています。
ベイズ推定は、条件付き確率を利用して、データが信念にどのように影響するかを理解するのに役立ちます。 空が赤いという以前の信念から始めたとしましょう。 いくつかのデータを見た後、私たちはすぐにこの以前の信念が間違っていることに気付くでしょう。 そのため、ベイズ更新を実行して、空の色に関する誤ったモデルを改善し、最終的にはより正確な事後確率を実現します。
データサイエンスに向けたマイケルバーク
条件付き確率
条件付き確率は、別のイベントが発生した場合のイベントの確率です。 つまり、条件BでのAの確率です。
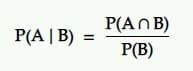
翻訳:別のイベントBが与えられたときにイベントAが発生する確率は、BとAが一緒に発生する確率をイベントBの確率で割ったものに等しくなります。
確率分布/尤度分布
尤度分布は、データが特定の値をとる可能性を示す分布です。
データが複数の値をとることができる場合、たとえば、灰色、赤、オレンジ、青などの色のようなカテゴリの場合、分布は多項分布になります。 一連の数値の場合、分布は正常である可能性があります。 また、yes/noまたはtrue/falseのいずれかのデータ値の場合、二項分布になります。
事前信念分布
または、単に事前確率と呼ばれる事前確率分布は、新しいデータの証拠を取得する前の信念を表します。 したがって、これは、ベイズ分析(または推論)を使用していくつかの証拠を検討した後に更新する最初の信念の表現です。
共役
まず第一に、共役とは、通常はペアで結合されることを指します。 ベイズ確率理論では、共役は事前確率が尤度に共役であると仮定しています。
事後確率が事前確率と同じ関数形式である場合、事前確率は尤度関数に共役です。 これは、尤度関数が事前分布を更新する方法を示しています。
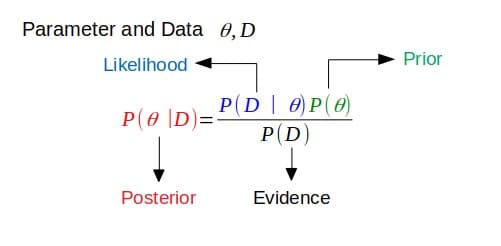
共役事前分布
これは上記の定義にリンクされています。 事後確率が事前確率分布と同じ確率分布ファミリーにある(または同じ関数形式を持っている)場合、事前分布と事後分布は共役分布です。 この場合、事前分布は尤度関数の共役事前分布と呼ばれます。
それらは、主観的(実験者の知識に基づく)、客観的で有益な(履歴データに基づく)、または非有益である可能性があります。
損失関数
損失関数は、現在の見積もりがどれほど悪いかを測定することによって損失を定量化する方法です。 これは、特に可能性のある値の範囲にある推論を表現する場合に、仮説検定の損失を最小限に抑え、検定結果による意思決定をサポートするのに役立ちます。
これで邪魔にならないので、次に進むことができます。
あなたがしばらくの間ブロックの周りにいたならば、あなたはおそらくいくつかの頻度主義者対ベイズ統計ミームに出くわしたでしょう。

双方が反対方向から答えを探しているように見えますが、それは本当ですか? これをよりよく理解するために(偏りのないまま)、頻度主義者キャンプに行きましょう。
頻度主義統計とは何ですか?
これは、ほとんどの人が統計で学ぶ最初の推論手法です。 頻度論的統計は、同じ条件下でイベント(仮説)が頻繁に発生する確率を計算します。
頻度主義的アプローチを使用したA/B仮説検定は、次の手順に従います。
- いくつかの仮説を宣言します。 通常、帰無仮説は、対立仮説が反対を宣言しているのに対し、新しいバリアント「B」は元の「A」よりも優れていないというものです。
- 逐次検定アプローチを使用している場合を除き、統計的検出力の計算を使用して事前にサンプルサイズを決定します。 統計的検出力、現在の変換率、および検出可能な最小効果を考慮したサンプルサイズ計算機を使用します。
- テストを実行し、各バリエーションが事前に決定されたサンプルサイズにさらされるのを待ちます。
- 帰無仮説(p値)の下でのデータと少なくとも同じくらい極端な結果を観測する確率を計算します。 p値が5%未満の場合は、帰無仮説を棄却し、新しいバリアントを本番環境にデプロイします。
これはベイジアンと比較してどうですか? どれどれ…
ベイジアンvs頻度主義A/Bテスト
これは、統計的推論が使用される場所で悪名高い議論です。 そして率直に言って、それは無意味です。 どちらにもメリットと、使用するのに最適な方法があります。
両方の陣営のほとんどのプロモーターがあなたに考えさせることとは反対に、彼らはいくつかの点で類似しており、どちらも他よりも真実に近づいていません—彼らのアプローチは異なりますが。
たとえば、A / Bテストに適用した場合、ビジネスの成長を引き起こす一連のアクションに関して、絶対的かつ正確な予測を提供する特定の方法はありません。 代わりに、A / Bテストは、意思決定からリスクを取り除くのに役立ちます。
ベイジアンまたは頻度主義的アプローチを使用してデータを分析する方法に関係なく、自分が正しいことをある程度確実に実行できます。
そのため、両方の統計モデルが有効です。 ベイジアンには速度の利点があるかもしれませんが、頻度主義者よりも計算量が多くなります。
他の違いをチェックしてください…
頻度主義フレームワーク
私たちのほとんどは、統計入門コースからの頻度主義的アプローチに精通しています。 帰無仮説の宣言、サンプルサイズの決定、ランダム化実験によるデータの収集、そして最後に統計的に有意な結果の観察から、上記の方法論を定義しました。
頻度主義では、確率は基本的に繰り返されるイベントの頻度に関連していると見なします。 したがって、公正なコイントスでは、頻度主義者は、十分な頻度で推測すれば、50%の確率で頭が正しくなり、尾も同じになると信じています。
頻度主義的考え方: 「同じ条件で何度も実験を繰り返すと、私の方法で正しい答えが得られる可能性はどのくらいありますか?」
ベイジアンフレームワーク
頻度主義的アプローチは、各バリアントの母集団パラメーターを(未知の)定数として扱いますが、ベイズアプローチは、各パラメーター値を確率分布を持つ確率変数としてモデル化します。
ここでは、対象のパラメーターの確率分布(したがって期待値)を直接計算します。
また、各バリアントの確率分布をモデル化するために、ベイズの定理に基づいて、実験結果を対象のメトリックについての事前知識と組み合わせます。 共役事前分布を使用すると、計算を簡略化できます。
Alex Birkettは、ベイズアルゴリズムを次のように要約しました。
- パラメータに関する主観的な信念を組み込んだ事前分布を定義します。 事前情報は、有益でない場合もあれば、有益な場合もあります。
- データを集めます。
- 事後分布を取得するには、ベイズの定理を使用して事前分布をデータで更新します(ただし、ベイズの規則を明示的に使用せずにベイズ法を使用できます。非パラメトリックベイズを参照してください)。 事後分布は、データを見た後のパラメーターに関する更新された信念を表す確率分布です。
- 事後分布を分析し、それを要約します(平均、中央値、標準偏差、分位数…)。
要するに、ベイズの実験者は彼ら自身の視点と彼らにとってどのような確率が意味するかに焦点を合わせています。 彼らの意見は、観察されたデータとともに進化します。 一方、頻度主義者は、正しい答えはどこかにあると信じています。

頻度主義的対ベイジアンの議論は、A/Bテスト後の分析にそれほど影響を与えないことを理解してください。 2つのキャンプの主な違いは、テストできる内容に関連しています。
確率統計は、通常、その後の分析ではあまり使用されません。 ベイジアン頻度論者の議論は、A / Bパラダイムでテストされる変数の選択に関してより適切ですが、ほとんどのA / Bテスターでさえ、研究仮説、確率、および信頼区間から地獄に違反しています。
ロブバロン博士からCXLへ
Georgiはさらに詳しく説明します。
複数のオンラインベイズ計算機と、ベイズ統計エンジンを適用する少なくとも1つの主要なA / Bテストソフトウェアベンダーがあります。これらはすべて、いわゆる非情報事前確率を使用します(少し誤解されていますが、これについては掘り下げません)。 ほとんどの場合、これらのツールの結果は、同じデータに対する頻度論的テストの結果と数値的に一致します。 ベイジアンツールが「BがAよりも優れている96%の確率」のようなものを報告し、頻度主義ツールが96%の信頼水準に対応する0.04のp値を生成するとします。
上記のような状況では、一部の人が認めるよりもはるかに一般的ですが、どちらの方法でも同じ推論が得られ、解釈が異なっていても不確実性のレベルは同じになります。
ベイジアンはこの結果について何と言いますか? 事前情報がないシナリオを表示するときに、p値を適切な事後確率に変換しますか? それとも、ベイジアンテストのこれらすべてのアプリケーションは、情報量の少ない事前確率自体を使用するために誤った方向に進んでいますか?
キャンプを選んで、他のキャンプに石を投げるためにカバーの後ろの場所を見つける必要は本当にありません。 両方のフレームワークが同じ結果を生み出すという証拠さえあります。 選択した道路に関係なく、目的地はおそらく同じになるでしょう。 それは、頻度主義的対ベイジアンでそこに到達する方法に依存します。
例えば:
- ベイジアンテストがより高速で、インタラクティブな実験に適していることを示すデータがあります。
ベイジアンパラダイムにより、実験者は信念を正式に定量化し、追加の知識を組み込むことができるため、従来の統計分析よりも高速です。
ベイジアンA/Bテストのシミュレーションでは、決定基準が調整された場合(つまり、ミスの許容度が高くなった場合)、実験の75%が、従来のアプローチで必要な観測値の22.7%以内で終了しました(5%の有意水準)。 そしてそれは10%のタイプIIエラーだけを記録しました。 - ベイジアンもより寛容であると考えられていますが、頻度主義者はリスクを嫌います:
多くの頻度論的テストは95%の統計的有意性を使用しますが、ベイジアンはそれ未満で満足することができます。 バリアントがコントロールを打ち負かす可能性が78%である場合、予想される損失に応じて、そのバリアントを「デプロイする」ことは適切な決定となる可能性があります。
あなたが間違っていて、期待損失が1%未満の場合、それは多くの企業にとってかなり重要な損害ではありません。 このごちゃごちゃしたアプローチは、非常にリスクの低いシナリオでの迅速な意思決定に適している可能性があります。 - ただし、ベイジアンシミュレーションと計算は計算量が多くなります。
一方、頻度主義者はペンと紙をベースにしています。 警告:A / Bテストツールがベイジアンを使用していて、データにどのような仮定が追加されているかわからない場合は、ベンダーからの「回答」に頼ることはできません。 塩を少し入れてください。 そして、独自の分析を実行します。
ベイジアンでは、すべてが太陽の光と虹ではありません。 Georgiがこの質問のリストで指摘しているように:
- 「事前確率と尤度関数の積を取得しますか?」
- 「事前確率とデータを出力として混合したいですか?」
- 「主観的な信念をデータと混合して出力を生成しますか?」 (有益な事前確率を使用する場合)
- 「実際のデータと非常に確実に混合されていると想定される事前情報がある統計を提示することに抵抗はありませんか?」
これらはすべて、素人の言葉で言えば、ベイズ統計の側面です。
ベイズ統計は、A / Bテストで実際に何を教えてくれますか?
A / Bテストは、コンバージョン率や訪問者1人あたりの収益など、変更が関心のある指標にどのように影響するかについての洞察を提供するように設計しました。
ベイズ統計で機能するツールを使用する場合、「Bが勝者」はほとんどの人が考えていることを正確に意味するわけではないため、結果の意味を理解することが重要です。
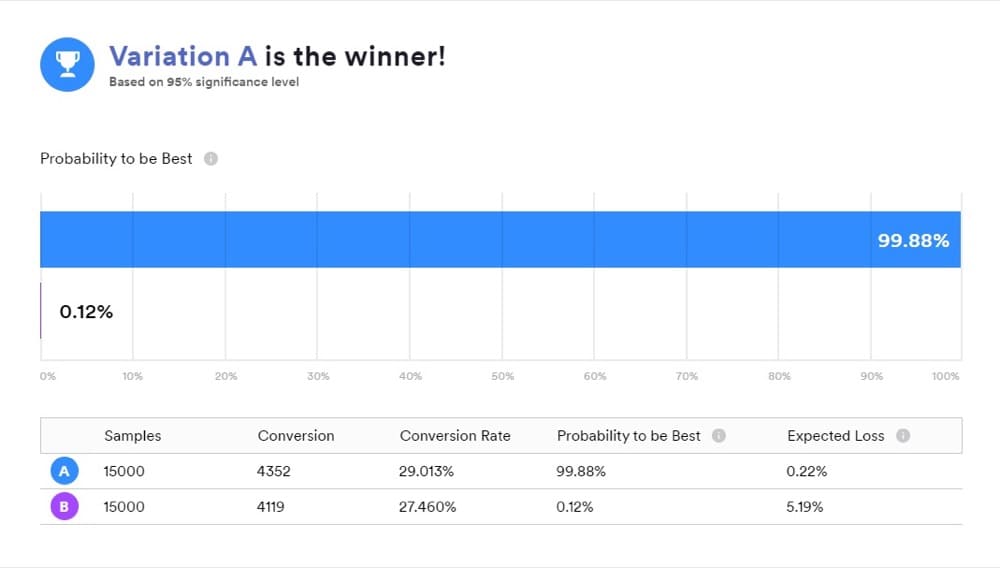
これは結果を提示するための便利な方法ですが、それはあなたのテストが明らかにしたものではありません。 代わりに、必要な答えは「A」と「B」の事後比較にあります。
比較の3つの方法は次のとおりです。
最高になる確率(P2BB)
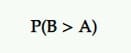
これは、ベイジアンA/Bテストで勝者を宣言する確率です。
最高の確率を持つバリアントは、他のバリアントを上回り続ける可能性が最も高いバリアントです。
これは、元のチャレンジャーとチャレンジャーからの対象のメジャーの事後サンプルのセットから計算されます。
たとえば、Bがコンバージョン率を上げる可能性が最も高い場合、Bが勝者として宣言されます。
予想される上昇
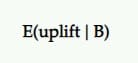
それで、Bが勝者である場合、それからどのくらいの上昇を期待する必要がありますか? テストで見たのと同じ結果を引き続き提供しますか?
これが、期待される隆起が提供しようとしている洞察です。 事後サンプルのセットが与えられた場合、AよりもBを選択することで予想される上昇は、増加率の信頼区間(または平均)として定義されます。
A / Bテストでは、通常、これをチャレンジャーとしてコントロールと比較します。 したがって、チャレンジャーが負けた場合は負の値(-11.35%など)で表され、勝った場合は正の値(+ 9.58%など)で表されます。
期待損失
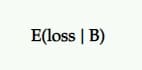
BがAよりも優れている確率は100%ではないため、AよりもBを選択すると、損失を記録する可能性があります。これは期待損失として表され、期待上昇と同様に、コントロールに対する挑戦者の視点。
これは、P2BBバリアント(つまり、宣言された勝者)を選択するリスクを示しています。
神話に飛び込む前に、分析の伝説であるGeorgiGeorgievに大いに感謝します。 頻度主義的推定とベイズ推定、およびA / Bテストにおけるベイズ確率と統計の彼の詳細な分析は、次のセクションに影響を与えました。
避けるべきベイズ統計に関する神話
不必要とほぼ同じくらい古いライバル関係で、ベイジアン対フリークエンティストの議論は多くのインプットを集めました—そして与えられた多くの神話に上昇します。
これらの神話の最大のもの(神話#2)は、A / Bテストツールのベンダーによって宣伝されており、一方のアプローチがもう一方のアプローチよりも優れている理由を説明しています。
しかし、上記のセクションを読んだ後、あなたはよりよく知っています。
これらの神話の穴を明らかにしましょう。
神話#1:ベイジアンは彼らの仮定を述べます、頻度主義者はしません
これは、ベイジアンが事前分布の形で仮定を行い、これらが評価のために開かれていることを示唆しています。 しかし、頻度主義者は、数学の真ん中に隠されている仮定をします。
なぜそれが間違っているのか:ベイジアンと頻度主義者は同様の基本的な仮定をしますが、唯一の違いは、ベイジアンが数学に加えて追加の仮定をすることです。
頻度主義モデルは、分布の形、観測間の効果の均一性または不均一性、観測の独立性など、数学の仮定を使用します。 そして、それらは隠されていません。 実際、それらは統計コミュニティで広く議論されており、すべての頻度論的統計検定について述べられています。
真実:頻度主義者は、仮定を明示的に述べ、仮定をテストするためにさらに一歩進んでいます:正規性のテスト、適合度テスト(サンプル比率の不一致テストがあります)など。
神話#2。 ベイジアン法はあなたが実際に望む答えをあなたに与える
ここでの誤解は、p値と信頼区間はテスターに知りたいことを伝えないのに対し、事後確率と信頼区間は伝えるというものです。 人々は次のようなことを知りたい
- BがAおよび
- 結果が偶然ではない可能性。
P値と仮説検定(直線推論)はその情報を提供しませんが、逆推論は提供します。
なぜそれが間違っているのか:これは言語学の問題です。 一般に、非統計家が「可能性」、「チャンス」、「確率」などの用語を使用する場合、技術的な意味を念頭に置いて使用していません。 深く調べてみると、逆推論については、まっすぐな推論と同じように混乱していることがわかります。
Georgi Georgievによると、次のような質問が出始めます。
- 「事前確率とは何ですか? それはどのような価値をもたらしますか?」
- 「尤度関数とは何ですか?」
- 「どのような「事前」確率、事前データがありませんか?」
- 「事前確率の選択をどのように擁護しますか?」
- 「これらの混合物を一切使用せずに、データの内容を正確に伝える方法はありますか?」
真実:専門用語の誤解ではなく、テスターが知りたいことについてより良い洞察が必要です。 P値、信頼区間などは、収集されたデータで結果がどれほど十分に調査されているかを示します。 それらは、主観的な、テストされていない事前の仮定の影響を受けずに確実性の尺度を提供しました。
神話#3:ベイジアン推論は頻度主義的推論よりも不確実性を伝えるのに役立ちます
テストの結果は、より「意味のある」洞察を生み出すからです。
なぜそれが間違っているのか:頻度主義的アプローチとベイジアンアプローチの両方に、確実性とA/Bテストの結果を伝えるのに役立つ同様のツールがあります。
| 頻度主義者 | ベイジアン | ||||||||||
| ●点推定 | ●点推定 | ||||||||||
| ●P値 | ●信頼区間 | ||||||||||
| ●信頼区間 | ●ベイズ因子 | ||||||||||
| ●P値曲線 | ●事後分布 (同じタスクを実行します 頻度主義曲線として) | ||||||||||
| ●信頼曲線 | |||||||||||
| ●重大度曲線など。 |
真実:それはすべてあなたがそれらをどのように使うかに依存します。 どちらの方法も、不確実性を伝えるのに等しく効果的です。 ただし、不確実性の尺度を提示する方法には違いがあります。
神話#4。 ベイジアンA/Bテストの結果は覗き見に耐性があります
一部のベイジアン統計学者は、「明確な勝者」が表示されたらベイジアンテストを停止でき、最終的な結果にはほとんど違いがないと主張しています。
これは頻度主義的テストでは受け入れられないことをおそらくご存知でしょう。したがって、ベイジアンと比較した場合、これは不利な点として数えられます。 しかし、それは本当にですか?
なぜそれが間違っているのか: 「データの蓄積に関する反復有意性検定」と題された王立統計学会誌の1969年の研究で、Armitageetal。 結果ベースのオプションの停止がエラー確率をどのように増加させるかを示しました。
ベイズ分析の動作を調整せずに、勝者に気付いたときに停止し、後部を更新して、次の事前情報として使用することはできません。
真実:覗き見は、頻度主義者と同じようにベイズ推定に影響を与えます(正しく実行したい場合)。
神話#5。 固定サンプルサイズを待たなければならないため、頻度主義統計は非効率的です
CROコミュニティの一部のメンバーは、頻度論的統計検定は固定された所定のサンプルサイズで実行する必要があると考えています。そうしないと、結果が無効になります。
その結果、必要な結果が得られるまで、必要以上に長く待機します。
なぜそれが間違っているのか:頻度主義統計は、現在約70年間そのように使用されていません。 頻度主義的逐次テストでは、事前に決められた一定の期間は必要ありません。
真実:今日より一般的な順次テストでは、タイプIとタイプIIのエラーのバランスをとるために最大サンプルサイズが必要ですが、実際に使用されるサンプルサイズは、観察された結果に応じてケースごとに異なります。
それで、あなたはベイジアンまたは頻度主義者を選ぶべきですか? 両方のための場所があります。
サイドを選ぶ必要はありません。 どちらの方法にも場所があります。 たとえば、更新された事前確率を使用し、迅速な結果を必要とする長期プロジェクトは、ベイジアンアプローチを使用する方が適切です。
一方、頻度主義的方法は、結果にかなりの再現性を必要とするプロジェクトに最適です。 多くのデータセットを持つ多くの人々が使用するソフトウェアの作成など。
Googleの意思決定インテリジェンスの責任者であるCassieKozyrkovが言うように、「統計は不確実性の下であなたの心を変える科学です」。
彼女のベイジアン対頻度主義統計の要約ビデオで、彼女は次のように述べています。
「その頻度主義的およびベイズ的議論を取り上げて、考えを変えようとしていることにすべてを崩壊させることができます。 頻度主義者は行動について考えを変えます。彼らは好ましいデフォルトの行動を持っています—おそらく彼らは何の信念も持っていません—しかし彼らは無知の下で好きな行動を持っていますそして彼らは尋ねますその行動?」 「自分の証拠に基づいてそれを行うのはばかげていると感じますか?」
一方、ベイジアンは別の方法で考えを変えます。 彼らは、事前意見と呼ばれる、数学的に表現された個人的な意見である意見から始め、次に、「いくつかの証拠を組み込んだ後、私が持つべき賢明な意見は何ですか?」と尋ねます。 そして、頻度主義者は行動についての考えを変え、ベイジアンは信念についての考えを変えます。
また、意思決定をどのように組み立てたいかによっては、一方のキャンプをもう一方のキャンプよりも優先する場合があります。」
結局、私たちは皆、同様の結論に向かっています—違いは、それらの結論があなたに提示される方法にあります。
頻度主義的推定とベイズ推定がプログラミング関数であり、入力が統計的な問題である場合、2つはユーザーに返すものが異なります。 頻度論的推定関数は推定値(通常はサンプル平均などの要約統計量)を表す数値を返しますが、ベイズ関数は確率を返します。
「ハッカーのための確率的プログラミングとベイズ法」という本からの抜粋
正しくないのは、一方が他方よりも実際的な結果をもたらすという主張です。
重要なポイント
A / Bテストのベイズ統計は、4つの異なるステップで構成されています。
- 以前の分布を特定する
- あなたの信念を反映する統計モデルを選択してください
- 実験を実行する
- 結果を使用して信念を更新し、事後分布を計算します
あなたの結果は洞察に満ちた確率にあなたを向けます。 したがって、どのバリアントが最良である可能性が最も高いか、予想される損失、および予想される上昇がわかります。
これらは通常、ベイズ統計を使用するほとんどのA/Bテストツールによって解釈されます。 しかし、徹底的な実験者は、これらの結果をよりよく理解するために、テスト後の分析を実行します。
あなたはこれまでにそれを成し遂げたので、ここにあなたにとって楽しい事実があります:あなたは誰もがよく知っているトーマスベイズの肖像画を知っていますか? これです:

それが彼だと100%確信している人は誰もいません。