Errori di tipo I e di tipo II: gli errori inevitabili nell'ottimizzazione

Gli errori di tipo I e di tipo II si verificano quando si individuano erroneamente i vincitori nei propri esperimenti o non si riesce a individuarli. Con entrambi gli errori, finisci per andare con ciò che sembra funzionare o meno. E non con i risultati reali.

Un'interpretazione errata dei risultati dei test non si traduce solo in sforzi di ottimizzazione fuorvianti, ma può anche far deragliare il tuo programma di ottimizzazione a lungo termine.

Il momento migliore per cogliere questi errori è prima ancora di commetterli! Vediamo quindi come evitare di incappare in errori di tipo I e di tipo II nei tuoi esperimenti di ottimizzazione.

Ma prima, diamo un'occhiata all'ipotesi nulla... perché è l'erroneo rifiuto o non rifiuto dell'ipotesi nulla che causa errori di tipo I e di tipo II .

L'ipotesi nulla: ​H0

Quando si ipotizza un esperimento, non si suggerisce direttamente che la modifica proposta sposterà una determinata metrica.

Inizi dicendo che la modifica proposta non influirà affatto sulla metrica interessata, che non sono correlate.

Questa è la tua ipotesi nulla (H0). H0 è sempre che non vi è alcun cambiamento. Questo è ciò in cui credi, per impostazione predefinita... finché (e se) il tuo esperimento non lo smentisce.

E la tua ipotesi alternativa (Ha o H1) è che ci sia un cambiamento positivo. H0 e Ha sono sempre opposti matematici. Ha è quello in cui ti aspetti che la modifica proposta faccia la differenza, è la tua ipotesi alternativa - e questo è ciò che stai testando con il tuo esperimento.

Quindi, ad esempio, se desideri eseguire un esperimento sulla tua pagina dei prezzi e aggiungervi un altro metodo di pagamento, devi prima formulare un'ipotesi nulla dicendo: il metodo di pagamento aggiuntivo non avrà alcun impatto sulle vendite. La tua ipotesi alternativa sarebbe: il metodo di pagamento aggiuntivo AUMENTA le vendite.

Condurre un esperimento, infatti, mette in discussione l'ipotesi nulla o lo status quo.

Gli errori di tipo I e di tipo II si verificano quando si rifiuta erroneamente o non si rifiuta l'ipotesi nulla.

Comprensione degli errori di tipo I

Gli errori di tipo I sono noti come falsi positivi o errori alfa.

In un'istanza di errore di tipo I di test di ipotesi, il test o l'esperimento di ottimizzazione * Sembra AVERE SUCCESSO* e tu (erroneamente) concludi che la variazione che stai testando sta facendo in modo diverso (migliore o peggiore) rispetto all'originale.

Negli errori di tipo I, vedi aumenti o cali - che sono solo temporanei e probabilmente non si manterranno a lungo termine - e finisci per rifiutare la tua ipotesi nulla (e accettare la tua ipotesi alternativa).

Rifiutare erroneamente l'ipotesi nulla può accadere per vari motivi, ma il principale è quello della pratica di sbirciare (cioè, guardare i risultati nel frattempo o quando l'esperimento è ancora in corso). E chiamare i test prima del raggiungimento dei criteri di arresto impostati.

Molte metodologie di test scoraggiano la pratica di sbirciare in quanto guardare i risultati intermedi potrebbe portare a conclusioni errate con conseguenti errori di tipo I.

Ecco come potresti fare un errore di tipo I:

Supponiamo che tu stia ottimizzando la pagina di destinazione del tuo sito Web B2B e ipotizza che l'aggiunta di badge o premi ridurrà l'ansia dei tuoi potenziali clienti, aumentando così il tasso di riempimento dei moduli (con conseguente maggior numero di lead).

Quindi la tua ipotesi nulla per questo esperimento diventa: l' aggiunta di badge non ha alcun impatto sui riempimenti dei moduli.

Il criterio di arresto per tale esperimento è solitamente un certo periodo e/o dopo che le conversioni X si verificano al livello di significatività statistica impostato. Convenzionalmente, gli ottimizzatori cercano di raggiungere il livello di confidenza statistica del 95% perché ti lascia con una probabilità del 5% di commettere l'errore di tipo I considerato sufficientemente basso per la maggior parte degli esperimenti di ottimizzazione. In generale, maggiore è questa metrica, minori sono le possibilità di commettere errori di tipo I.

Il livello di confidenza a cui miri determina quale sarà la tua probabilità di ottenere un errore di tipo I (α).

Quindi, se miri a un livello di confidenza del 95%, il tuo valore per α diventa 5%. Qui, accetti che c'è una probabilità del 5% che la tua conclusione possa essere sbagliata.

Al contrario, se scegli un livello di confidenza del 99% con il tuo esperimento, la tua probabilità di ottenere un errore di tipo I scende all'1%.

Diciamo, per questo esperimento, che diventi troppo impaziente e invece di aspettare che l'esperimento finisca, guardi la dashboard del tuo strumento di test (sbircia!) solo un giorno dopo. E noti un aumento "apparente": il tasso di riempimento dei moduli è aumentato di un enorme 29,2% con un livello di fiducia del 95%.

E BAM...

... interrompi il tuo esperimento.

… rifiutare l'ipotesi nulla (che i badge non avessero alcun impatto sulle vendite).

… accettare l'ipotesi alternativa (che i badge abbiano aumentato le vendite).

… e corri con la versione con i badge dei premi.

Ma mentre misuri i tuoi lead nel corso del mese, trovi che il numero è quasi paragonabile a quello che hai segnalato con la versione originale. Dopotutto, i badge non contavano molto. E che l'ipotesi nulla è stata probabilmente respinta invano.

Quello che è successo qui è che hai terminato il tuo esperimento troppo presto e hai rifiutato l'ipotesi nulla e hai finito con un falso vincitore, commettendo un errore di tipo I.

Come evitare errori di tipo I nei tuoi esperimenti

Un modo sicuro per ridurre le possibilità di ottenere un errore di tipo I è utilizzare un livello di confidenza più elevato. È accettabile un livello di significatività statistica del 5% (che si traduce in un livello di confidenza statistica del 95%). È una scommessa che la maggior parte degli ottimizzatori farebbe in sicurezza perché, qui, fallirai nell'improbabile intervallo del 5%.

Oltre a impostare un livello di confidenza elevato, è importante eseguire i test abbastanza a lungo. I calcolatori della durata del test possono dirti per quanto tempo devi eseguire il test (dopo aver preso in considerazione cose come una dimensione dell'effetto specificata, tra le altre). Se lasci che un esperimento esegua il suo corso previsto, riduci significativamente le possibilità di riscontrare l'errore di tipo 1 (dato che stai utilizzando un livello di confidenza elevato). Aspettare di raggiungere risultati statisticamente significativi assicura che ci sia solo una bassa probabilità (di solito il 5%) che tu abbia rifiutato erroneamente l'ipotesi nulla e commesso un errore di tipo I. In altre parole, utilizzare una buona dimensione del campione perché è fondamentale per ottenere risultati statisticamente significativi.

Ora si trattava di errori di tipo I correlati al livello di confidenza (o significato) nei tuoi esperimenti. Ma c'è anche un altro tipo di errore che può insinuarsi nei tuoi test: gli errori di tipo II.

Comprensione degli errori di tipo II

Gli errori di tipo II sono noti come falsi negativi o errori beta.

In contrasto con l'errore di tipo I, nel caso di un errore di tipo II, l'esperimento *Sembra NON SUCCESSIVO (O INCONCLUSO)* e tu (erroneamente) concludi che la variazione che stai testando non è diversa dall'errore originale.

Negli errori di tipo II, non riesci a vedere i veri aumenti o cali e finisci per non rifiutare l'ipotesi nulla e rifiutare l'ipotesi alternativa.

Ecco come potresti fare l'errore di tipo II:

Tornando allo stesso sito Web B2B dall'alto...

Quindi supponiamo che questa volta tu ipotizzi che l'aggiunta di un disclaimer di conformità al GDPR in primo piano nella parte superiore del tuo modulo incoraggerà più potenziali clienti a compilarlo (con conseguente maggior numero di lead).

Pertanto, la tua ipotesi nulla per questo esperimento diventa: L'esclusione di responsabilità per la conformità al GDPR non influisce sui riempimenti dei moduli.

E l'ipotesi alternativa per lo stesso recita: il disclaimer di conformità al GDPR comporta più riempimenti di moduli.

La potenza statistica di un test determina quanto bene può rilevare le differenze nelle prestazioni delle versioni originale e challenger, in caso di scostamenti. Tradizionalmente, gli ottimizzatori cercano di raggiungere l'80% di potenza statistica perché maggiore è questa metrica, minori sono le possibilità di commettere errori di tipo II.

La potenza statistica assume un valore compreso tra 0 e 1 (ed è spesso espressa in %) e controlla la probabilità del tuo errore di tipo II (β); è calcolato come: 1 – β

Maggiore è la potenza statistica del test, minore sarà la probabilità di incontrare errori di tipo II.

Quindi, se un esperimento ha una potenza statistica del 10%, può essere abbastanza suscettibile a un errore di tipo II. Considerando che, se un esperimento ha una potenza statistica dell'80%, sarà molto meno probabile che commetta un errore di tipo II.

Ancora una volta, esegui il test, ma questa volta non noti alcun miglioramento significativo nei riempimenti dei moduli. Entrambe le versioni riportano conversioni quasi simili. Per questo motivo, interrompi l'esperimento e prosegui con la versione originale senza l'esclusione di responsabilità per la conformità al GDPR.

Tuttavia, mentre approfondisci i dati sui lead del periodo dell'esperimento, scopri che mentre il numero di lead di entrambe le versioni (l'originale e la sfidante) sembrava identico, la versione GDPR ti ha fatto ottenere un buon aumento significativo del numero di lead dall'Europa. (Naturalmente, avresti potuto utilizzare il targeting per pubblico per mostrare l'esperimento solo ai lead dall'Europa, ma questa è un'altra storia.)

Quello che è successo qui è che hai terminato il tuo test troppo presto, senza controllare se avevi raggiunto una potenza sufficiente, commettendo un errore di tipo II.

Come evitare errori di tipo II nei tuoi esperimenti

Per evitare errori di tipo II, eseguire test con un'elevata potenza statistica. Prova a configurare i tuoi esperimenti in modo da poter raggiungere almeno l'80% di potenza statistica. Questo è un livello accettabile di potenza statistica per la maggior parte degli esperimenti di ottimizzazione. Con esso, puoi assicurarti che nell'80% dei casi, almeno, rifiuterai correttamente un'ipotesi nulla falsa.

Per fare ciò, è necessario guardare i fattori che si aggiungono.

Il più grande di questi è la dimensione del campione (data una dimensione dell'effetto osservato). La dimensione del campione si lega direttamente alla potenza di un test. Un'enorme dimensione del campione significa un test ad alta potenza. I test sottodimensionati sono molto vulnerabili agli errori di tipo II poiché le tue possibilità di rilevare differenze nei risultati del tuo sfidante e delle versioni originali si riducono notevolmente, specialmente per MEI bassi (maggiori informazioni di seguito). Quindi, per evitare errori di tipo II, attendere che il test accumuli potenza sufficiente per ridurre al minimo gli errori di tipo II. Idealmente, nella maggior parte dei casi, dovresti raggiungere una potenza di almeno l'80%.

Un altro fattore è l' effetto minimo di interesse (MEI) a cui si rivolge l'esperimento. MEI (chiamato anche MDE) è l'entità minima della differenza che vorresti rilevare nel tuo KPI in questione. Se imposti un MEI basso (osservando un aumento dell'1,5%, ad esempio), le tue possibilità di incontrare l'errore di tipo II aumentano perché il rilevamento di piccole differenze richiede campioni di dimensioni sostanzialmente maggiori (per ottenere una potenza sufficiente).

Infine, è importante notare che tende ad esserci una relazione inversa tra la probabilità di commettere un errore di tipo I (α) e la probabilità di commettere un errore di tipo II (β). Ad esempio, se riduci il valore di α per ridurre la probabilità di commettere un errore di tipo I (diciamo di impostare α all'1%, che significa un livello di confidenza del 99%), la potenza statistica del tuo esperimento (o la sua capacità, β , di rilevare una differenza quando esiste) finisce anche per ridurre, aumentando così la probabilità di ottenere un errore di tipo II.

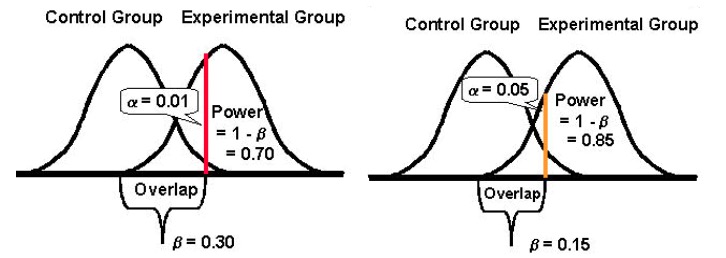
Accettare di più entrambi gli errori: tipo I e II (e trovare un equilibrio)

Diminuendo la probabilità di un tipo di errore si aumenta quella dell'altro tipo (dato che tutto il resto rimane lo stesso).

E quindi devi rispondere alla chiamata su quale tipo di errore potresti essere più tollerante.

Commettere un errore di tipo I, da un lato, e implementare una modifica per tutti i tuoi utenti potrebbe costarti conversioni ed entrate e, peggio ancora, potrebbe anche essere un killer di conversioni.

Commettere un errore di tipo II, d'altra parte, e non distribuire una versione vincente per tutti i tuoi utenti potrebbe, ancora una volta, costarti le conversioni che avresti altrimenti vinto.

Invariabilmente, entrambi gli errori hanno un costo.

Tuttavia, a seconda del tuo esperimento, uno potrebbe essere più accettabile per te rispetto all'altro. In generale, i tester trovano l' errore di tipo I circa quattro volte più grave dell'errore di tipo II .

Se desideri adottare un approccio più equilibrato, lo statistico Jacob Cohen suggerisce che dovresti optare per una potenza statistica dell'80% che viene fornita con “ un ragionevole equilibrio tra rischio alfa e beta. ” (l'80% di potenza è anche lo standard per la maggior parte degli strumenti di test.)

E per quanto riguarda la significatività statistica, lo standard è fissato al 95%.

Fondamentalmente, si tratta di compromessi e del livello di rischio che sei disposto a tollerare. Se volessi davvero ridurre al minimo le possibilità di entrambi gli errori, potresti optare per un livello di confidenza del 99% e una potenza del 99%. Ma ciò significherebbe che lavoreresti con campioni di dimensioni incredibilmente grandi per periodi che sembrano eternamente lunghi. Inoltre, anche allora lasceresti un margine di errore.

Ogni tanto, concluderai un esperimento in modo sbagliato. Ma questo fa parte del processo di test: ci vuole del tempo per padroneggiare le statistiche dei test A/B. Indagare e testare nuovamente o dare seguito ai tuoi esperimenti riusciti o falliti è un modo per riaffermare le tue scoperte o scoprire di aver commesso un errore.