Rete neurale a neurone singolo su Python - Con intuizione matematica

Costruiamo una rete semplice, molto molto semplice, ma completa, con un unico livello. Solo un input — e un neurone (che è anche l'output), un peso, un bias.

Eseguiamo prima il codice e poi analizziamo parte per parte

Clona il progetto Github o esegui semplicemente il codice seguente nel tuo IDE preferito.

Se hai bisogno di aiuto per configurare un IDE, ho descritto il processo qui.

Se tutto va bene, otterrai questo output:

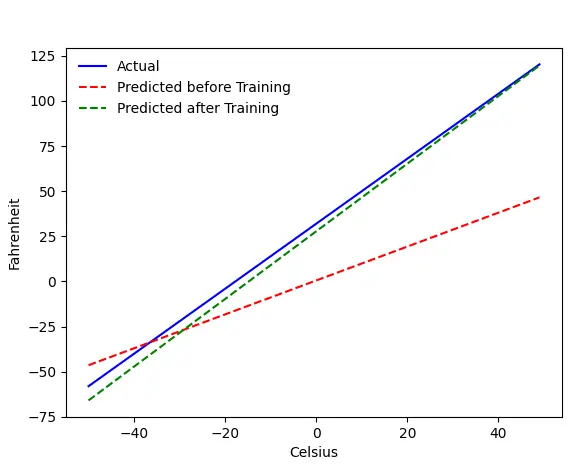
Il problema — Fahrenheit da Celsius

Addestreremo la nostra macchina per prevedere Fahrenheit da Celsius. Come puoi capire dal codice (o dal grafico), la linea blu è l'effettiva relazione Celsius-Fahrenheit. La linea rossa è la relazione prevista dalla nostra macchina per bambini senza alcun allenamento. Infine, alleniamo la macchina e la linea verde è la previsione dopo l'allenamento.

Guarda Line#65–67: prima e dopo l'allenamento, prevede l'utilizzo della stessa funzione ( get_predicted_fahrenheit_values() ). Quindi cosa sta facendo magic train()? Scopriamolo.

Struttura di rete

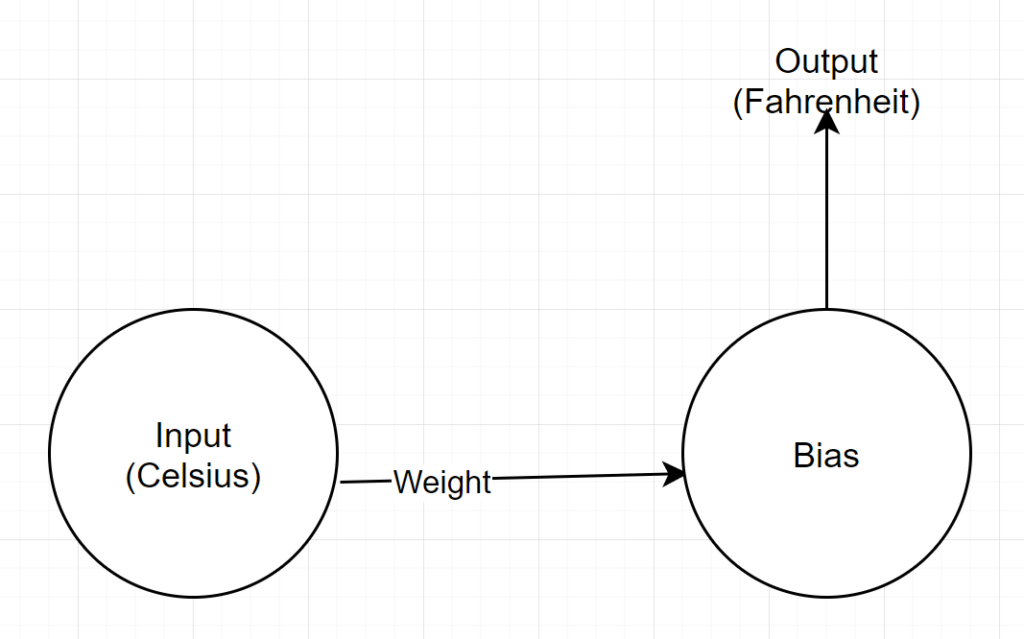
Input: un numero che rappresenta centigradi

Peso: un galleggiante che rappresenta il peso

Bias: un float che rappresenta il bias

Output: un float che rappresenta il Fahrenheit previsto

Quindi, abbiamo un totale di 2 parametri: 1 peso e 1 distorsione

Analisi del codice

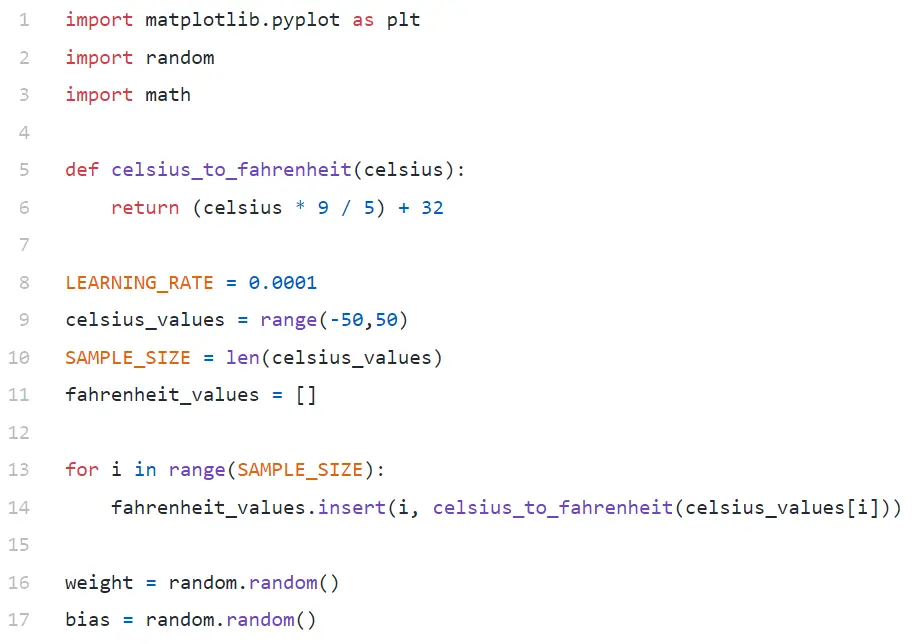
In Line#9, stiamo generando un array di 100 numeri compresi tra -50 e +50 (escluso 50 — la funzione range esclude il valore limite superiore).

In Line#11–14, stiamo generando il Fahrenheit per ogni valore Celsius.

Nelle righe n. 16 e n. 17, stiamo inizializzando peso e bias.

treno()

Stiamo eseguendo 10000 iterazioni di formazione qui. Ogni iterazione è composta da:

1. passaggio in avanti (Linea#57).
2. passaggio all'indietro (Linea#58).
3. update_parameters (Linea#59)

Se non conosci Python, potrebbe sembrarti un po' strano: le funzioni python possono restituire più valori come tuple .

Si noti che update_parameters è l'unica cosa che ci interessa. Tutto il resto che stiamo facendo qui è valutare i parametri di questa funzione, che sono i gradienti (spiegheremo di seguito quali sono i gradienti) del nostro peso e bias.

1. grad_weight: un float che rappresenta il gradiente di peso
2. grad_bias: un float che rappresenta il gradiente di bias

Otteniamo questi valori chiamando all'indietro, ma richiede l'output, che otteniamo chiamando in avanti alla riga n. 57.

inoltrare()

Si noti che qui celsius_values ​​e fahrenheit_values ​​sono array di 100 righe:

Dopo aver eseguito Line#20–23, per un valore celsius, diciamo 42

uscita = 42 * peso + bias

Quindi, per 100 elementi in celsius_values ​​, l'output sarà una matrice di 100 elementi per ogni valore celsius corrispondente.

La riga n. 25–30 calcola la perdita utilizzando la funzione di perdita dell'errore quadratico medio (MSE), che è solo un nome di fantasia del quadrato di tutte le differenze diviso per il numero di campioni (100 in questo caso).

Una piccola perdita significa una migliore previsione. Se continui a stampare la perdita in ogni iterazione, vedrai che sta diminuendo con il progredire della formazione.

Infine, nella riga n. 31 stiamo restituendo l'output e la perdita previsti.

indietro

Siamo interessati solo ad aggiornare il nostro peso e bias. Per aggiornare quei valori, dobbiamo conoscere i loro gradienti, ed è quello che stiamo calcolando qui.

I gradienti di avviso vengono calcolati in ordine inverso. Viene prima calcolato il gradiente di output, quindi il peso e il bias, quindi il nome "backpropagation". Il motivo è che, per calcolare il gradiente di peso e bias, dobbiamo conoscere il gradiente di output, in modo da poterlo utilizzare nella formula della regola della catena .

Ora diamo un'occhiata a cosa sono il gradiente e la regola della catena.

Pendenza

Per semplicità, considera che abbiamo un solo valore di celsius_values ​​e fahrenheit_values ​​, rispettivamente 42 e 107.6 .

Ora, la ripartizione del calcolo nella riga n. 30 diventa:

perdita = (107,6 — (42 * peso + bias))² / 1

Come vedi, la perdita dipende da 2 parametri: pesi e bias. Considera il peso. Immagina di averlo inizializzato con un valore casuale, diciamo, 0,8, e dopo aver valutato l'equazione sopra, otteniamo 123,45 come valore della perdita . Sulla base di questo valore di perdita, devi decidere come aggiornerai il peso. Dovresti renderlo 0.9 o 0.7?

Devi aggiornare il peso in modo tale che nella prossima iterazione ottieni un valore inferiore per la perdita (ricorda, ridurre al minimo la perdita è l'obiettivo finale). Quindi, se l'aumento di peso aumenta la perdita, la diminuiamo. E se l'aumento di peso diminuisce la perdita, la aumenteremo.

Ora, la domanda, come facciamo a sapere se l'aumento dei pesi aumenterà o diminuirà la perdita. È qui che entra in gioco il gradiente . In generale, il gradiente è definito da derivata. Ricorda dal calcolo del tuo liceo, ∂y/∂x (che è derivata/gradiente parziale di y rispetto a x) indica come y cambierà con una piccola variazione in x.

Se ∂y/∂x è positivo, significa che un piccolo incremento di x aumenterà y.

Se ∂y/∂x è negativo, significa che un piccolo incremento di x diminuirà y.

Se ∂y/∂x è grande, una piccola variazione in x causerà una grande variazione in y.

Se ∂y/∂x è piccolo, una piccola variazione in x causerà una piccola variazione in y.

Quindi, dai gradienti, otteniamo 2 informazioni. In quale direzione deve essere aggiornato il parametro (aumento o diminuzione) e quanto (grande o piccolo).

Regola di derivazione

Informalmente, la regola della catena dice:

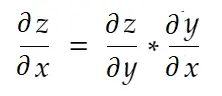
Considera l'esempio di peso sopra. Dobbiamo calcolare grad_weight per aggiornare questo peso, che verrà calcolato da:

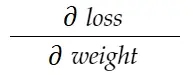
Con la formula della regola della catena, possiamo derivarla:

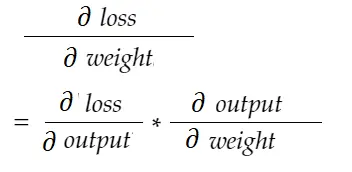
Allo stesso modo, gradiente per bias:

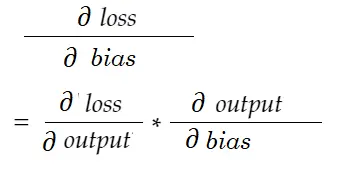
Disegniamo un diagramma delle dipendenze.

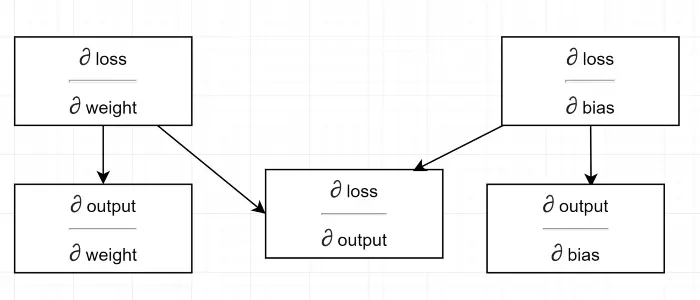
Vedi tutti i calcoli dipendono dal gradiente di uscita (∂ perdita/∂ uscita) . Questo è il motivo per cui lo stiamo calcolando prima sul backpass (Linea n. 34–36).

In effetti, nei framework ML di alto livello, ad esempio in PyTorch, non è necessario scrivere codici per il backpass! Durante il passaggio in avanti, crea grafici di calcolo e durante il passaggio all'indietro, attraversa la direzione opposta nel grafico e calcola i gradienti utilizzando la regola della catena.

∂ perdita / ∂ uscita

Definiamo questa variabile da grad_output nel codice, che abbiamo calcolato in Line#34–36. Scopriamo il motivo dietro la formula che abbiamo usato nel codice.

Ricorda, stiamo alimentando insieme tutti i 100 valori_celsius nella macchina. Quindi, grad_output sarà un array di 100 elementi, ogni elemento contenente gradiente di output per l'elemento corrispondente in celsius_values ​​. Per semplicità, consideriamo che ci sono solo 2 elementi in celsius_values ​​.

Quindi, scomponendo la riga n. 30,

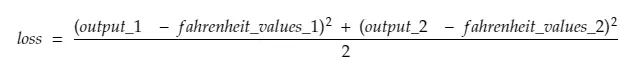
dove,

output_1 = valore di output per il 1° valore celsius

output_2 = valore di output per il 2° valore celsius

fahreinheit_values_1 = Valore fahreinheit effettivo per il 1° valore Celsius

fahreinheit_values_1 = Valore fahreinheit effettivo per il 2° valore Celsius

Ora, la variabile risultante grad_output conterrà 2 valori — gradiente di output_1 e output_2, che significa:

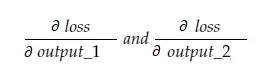
Calcoliamo solo il gradiente di output_1, quindi possiamo applicare la stessa regola per gli altri.

Tempo di calcolo!

Che è lo stesso della riga # 34–36.

Gradiente di peso

Immagina di avere un solo elemento in celsius_values. Adesso:

Che è lo stesso della riga n. 38–40. Per 100 celsius_values, verranno sommati i valori del gradiente per ciascuno dei valori. Una domanda ovvia sarebbe perché non stiamo ridimensionando il risultato (cioè dividendo con SAMPLE_SIZE). Poiché moltiplichiamo tutti i gradienti con un piccolo fattore prima di aggiornare i parametri, non è necessario (vedi l'ultima sezione Aggiornamento dei parametri).

Gradiente di distorsione

Che è lo stesso della riga n. 42. Come i gradienti di peso, questi valori per ciascuno dei 100 input vengono sommati. Ancora una volta, va bene poiché i gradienti vengono moltiplicati per un piccolo fattore prima di aggiornare i parametri.

Aggiornamento dei parametri

Infine, stiamo aggiornando i parametri. Si noti che i gradienti moltiplicati per un piccolo fattore (LEARNING_RATE) prima di essere sottratti, per rendere stabile l'allenamento. Un valore grande di LEARNING_RATE causerà un problema di superamento e un valore estremamente piccolo renderà l'allenamento più lento, che potrebbe richiedere molte più iterazioni. Dovremmo trovare un valore ottimale per esso con alcuni tentativi ed errori. Ci sono molte risorse online su di esso, inclusa questa per saperne di più sull'apprendimento Rate.

Si noti che l'importo esatto che aggiustiamo non è estremamente critico. Ad esempio, se si sintonizza un po' LEARNING_RATE, le variabili discesa_grad_peso e discesa_grad_bias (Linea#49–50) verranno modificate, ma la macchina potrebbe continuare a funzionare. L'importante è assicurarsi che questi importi siano derivati ​​ridimensionando i gradienti con lo stesso fattore (LEARNING_RATE in questo caso). In altre parole, “mantenere proporzionale la discesa dei dislivelli” conta più di “quanto scendono ”.

Si noti inoltre che questi valori di gradiente sono in realtà la somma dei gradienti valutati per ciascuno dei 100 input. Ma poiché questi sono ridimensionati con lo stesso valore, va bene come menzionato sopra.

Per aggiornare i parametri, dobbiamo dichiararli con la parola chiave globale (in Line#47).

Dove andare da qui

Il codice sarebbe molto più piccolo sostituendo i cicli for con la comprensione dell'elenco in modo pythonic. Dai un'occhiata ora: non ci vorrebbero più di pochi minuti per capirlo.

Se hai capito tutto finora, probabilmente è un buon momento per vedere gli interni di una semplice rete con più neuroni/strati: ecco un articolo.