Distribuzione normale: un'introduzione intuitiva senza matematica

Cercherò di mantenere questo articolo libero da equazioni e gergo boccone, per quanto possibile. Tuttavia, ho bisogno che tu abbia almeno le seguenti capacità:

• Capace di interpretare semplici grafici.
• Conoscenza di livello elementare in probabilità. Almeno capisci che c'è una probabilità del 50% per la testa se lancio una moneta.
• Calcolo integrale e fisica quantistica (scherzo!)

Perché la distribuzione normale

Un modo intuitivo per capire qualcosa è indagare perché è necessario. Facciamolo per la distribuzione normale (chiamata anche distribuzione gaussiana).

Di' che hai una strana abitudine. Ogni giorno lanci una moneta 100 volte. È "normale" aspettarsi di avere la testa 50 volte - o quasi 50 volte per la maggior parte della giornata. Raramente, ci sono giorni buoni per la testa: potresti ottenere circa 55 volte e molto raramente oltre 65 volte.

Ora, vuoi quantificare questa "rarità". Quindi, inizi a tenere traccia di quante volte hai avuto la testa ogni giorno.

Numero di teste ogni giorno in un anno

Di seguito sono riportati i dati dopo un anno (365 giorni): il primo è il numero di teste che hai ricevuto il primo giorno e l'ultimo è il numero di teste che hai ottenuto l'ultimo giorno. Non è necessario controllare tutti i numeri di seguito, ma è facile notare che la maggior parte di essi è intorno a 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Visualizza meglio con l'istogramma

Tracciamo un istogramma dai dati sopra:

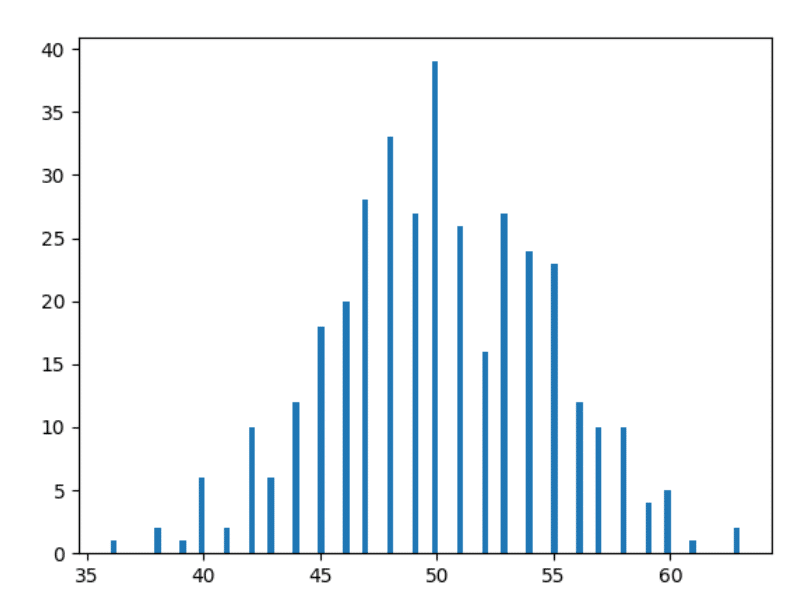
Ah! Non sembra già l'immagine che hai visto su Internet quando hai cercato su Google "Distribuzione normale"? Siamo quasi li!

Quindi, se non capisci gli istogrammi, abbiamo appena tracciato qui il numero di giorni in cui abbiamo ottenuto un conteggio particolare per capi. Ad esempio, abbiamo avuto la testa 36 volte in 2 giorni particolari dell'anno (controlla i dati sopra se non mi credi), ecco perché c'è una barra di altezza 2 unità sul punto orizzontale a 36 (il rosso rettangolo a sinistra nell'immagine sottostante).

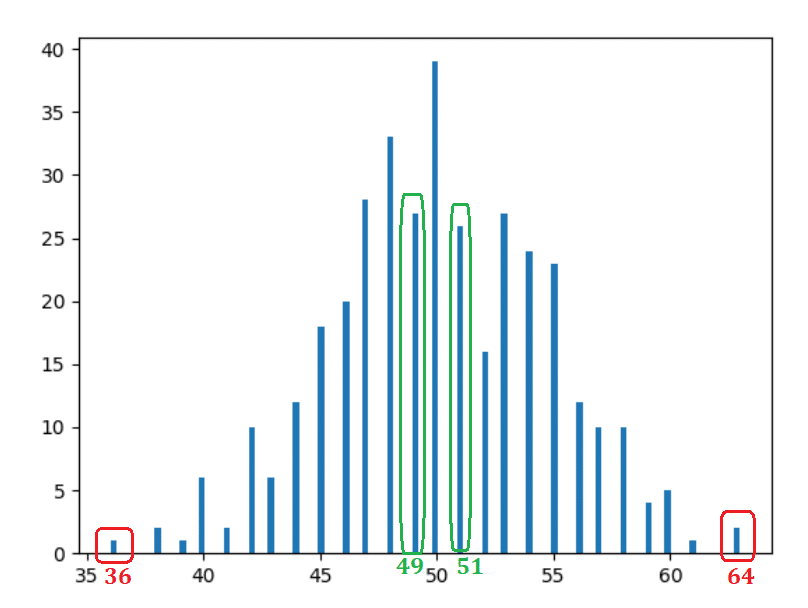
Osservazioni

1. Abbastanza ovvio e previsto: 50 teste si sono verificate la maggior parte delle volte.
2. Più ci allontaniamo dal centro (50), l'incidenza è per lo più in diminuzione.
3. Le barre alla stessa distanza assumono forme simili. Ad esempio, se si sposta un'unità a sinistra (49) oa destra (51) — le occorrenze sono simili — rispettivamente 30 e 31 (i rettangoli verdi). Se sposti 14 unità a sinistra (36) oa destra (64), le occorrenze sono di nuovo simili: rispettivamente 2 e 1 (rettangoli rossi).

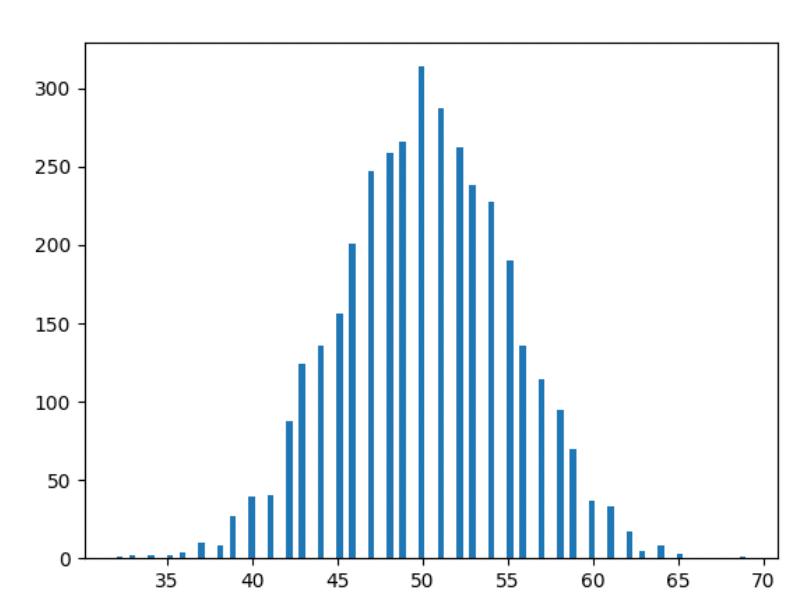
Dati a 10 anni

Ora andiamo avanti un po' e tracciamo i dati di 10 anni.

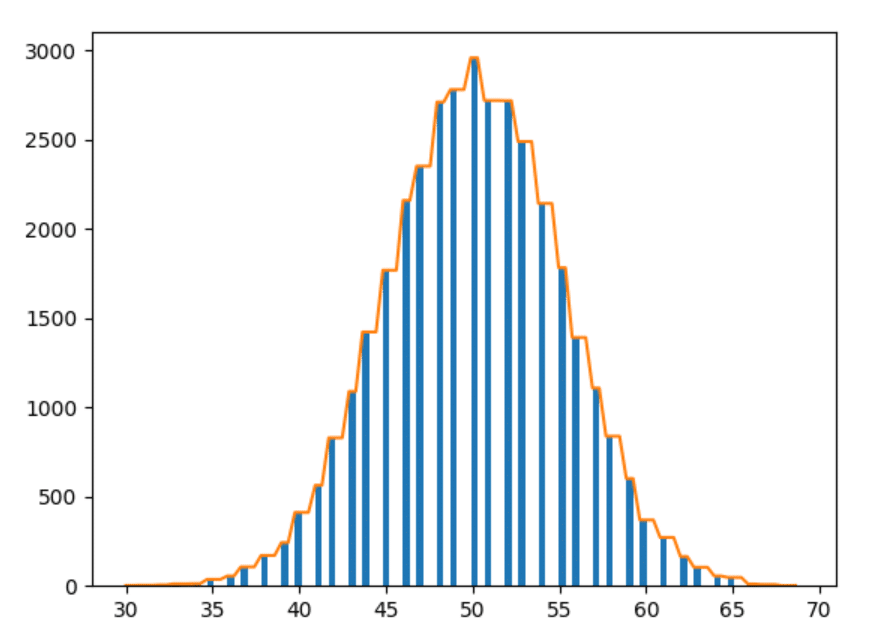
1000 anni di dati

Ok, l'ultimo. Tracciamo i dati di 1000 anni.

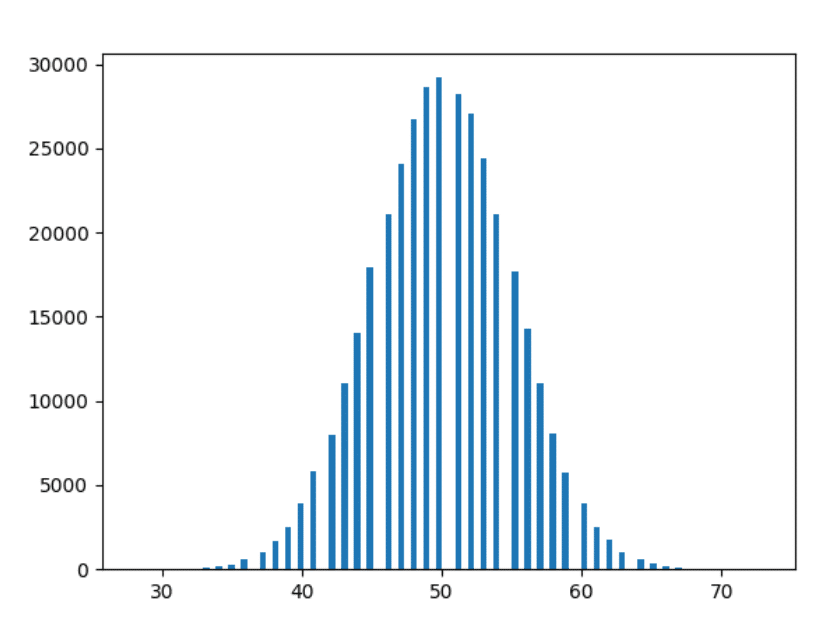
Osservazioni

1. Più sperimentiamo, più morbide sono le forme.
2. Più sperimentiamo, più le barre seguono le osservazioni di cui sopra (cioè le barre a una distanza simile stanno assumendo forme più vicine).

Dov'è la maledetta distribuzione normale

Va bene - troppo background - ora andiamo al punto.

Vediamo la risposta suggerita da Google:

Alcune cose in questa definizione:

Variabile casuale: in poche parole: una variabile casuale è un insieme di possibili valori di un esperimento casuale come il lancio di una moneta. Nel nostro esempio, il possibile valore del nostro esperimento è Head or Tail .

A forma di campana: hai notato che il nostro istogramma sta assumendo una forma a campana?

Simmetrico: le barre alla stessa distanza hanno forme simili, non è simmetrico?

Quindi, la distribuzione normale rappresenta la distribuzione dei risultati per eventi come il lancio della moneta, in cui la distribuzione tende a mantenere alcune proprietà, tra cui la simmetria e la forma della campana.

Quali fenomeni oltre al lancio della moneta seguono la distribuzione normale?

Alcuni esempi interessanti qui.

• Altezza nella popolazione: più persone rientrano nel gruppo di altezza media. È raro trovare persone estremamente alte o estremamente basse. E le possibilità di trovarsi estremamente alto ed estremamente basso sono quasi uguali.
• Tirare un dado
• Taglia di scarpe
• QI
• E molto altro...

Questi fenomeni seguono rigorosamente la distribuzione normale?

La risposta semplice è no. Sebbene, come abbiamo visto sopra, più sperimenti, più i dati seguiranno le normali proprietà di distribuzione. Ma non vi è alcuna garanzia che qualche evento improbabile non si verificherà comunque.

Tutte le distribuzioni di probabilità nell'universo sono distribuzioni normali?

No. Ci sono molti fenomeni che sono determinati da qualche altro tipo di distribuzione.

• La probabilità che un determinato numero di clienti arrivi, telefonate, incidenti, eventi sportivi e inondazioni seguono la distribuzione di Poisson .
• Per le vendite aziendali, il 20% dei clienti di un'azienda è responsabile dell'80% delle vendite. ( Distribuzione Paretiana )
• Modelli di traffico in una città — Distribuzione esponenziale
• Selezione casuale di membri per una squadra da una popolazione di ragazze e ragazzi — Distribuzione ipergeometrica

E tanti altri …

Ho prodotto l'elenco sopra semplicemente cercando su Google "esempi di vita reale" con alcune distribuzioni elencate qui, non che le comprenda tutte. 😉

C'è una ragione per cui alcuni fenomeni naturali tendono a seguire la distribuzione normale

Sì, citando la mia spiegazione preferita:

La spiegazione usuale è data da un altro nome per la distribuzione normale, che è la “distribuzione degli errori”. L'idea è che gli errori siano generalmente casuali, quindi è probabile che vadano in una direzione come nell'altra. Ad esempio, è probabile che il tiratore tiri un po' a sinistra, un po' a destra, o un po' in alto quanto un po' in basso. Pertanto, un grafico della distanza dei colpi dal bullseye rifletterà questa tendenza casuale e sarà simmetrico rispetto alla media. Allo stesso modo, con l'altezza e l'intelligenza, molti geni (forse migliaia) contribuiscono a questi risultati, così come un gran numero di fattori ambientali, come alimentazione, malattie, basso reddito e così via.

Parametri di distribuzione normale

Se hai avuto un'intuizione della discussione finora, sei già il vincitore. Missione compiuta. Il resto dell'articolo è un bonus.

Tutti i grafici di distribuzione normale che vedi hanno una forma diversa. Alcuni di loro sono più piatti di altri. Alcuni di loro hanno buone altezze. Tutte queste forme sono controllate da soli 2 parametri:

Significare

La media è definita dalla media. Definisce l'altezza della campana. Per l'esempio del lancio della moneta, la media è vicina a 50, che è la posizione in alto nel grafico.

Deviazione standard

Poiché prometto che questo articolo sarà privo di equazioni, non sto fornendo qui la sua rappresentazione matematica. Ma comunque non è così difficile. La deviazione standard è una metrica per rappresentare la diversità dei dati.

Ad esempio, la deviazione standard dell'età nell'assistenza all'infanzia sarà inferiore alla deviazione standard dell'età nel club dei tifosi, poiché il divario di età tra il gruppo più giovane e quello più anziano dovrebbe essere molto più alto nel club dei tifosi.

La deviazione standard determina la larghezza della curva. Una piccola deviazione standard produce una curva ripida e una deviazione standard più grande produce una curva più piatta.