Statistiche bayesiane: Primer rapido e senza clamore di un tester A/B
Pubblicato: 2022-06-23
Quanto sei sicuro della tua capacità di interpretare i risultati forniti dal tuo strumento di test A/B?
Supponiamo che tu stia utilizzando uno strumento basato su statistiche bayesiane e ti dice che "B" ha una probabilità del 70% di battere "A", quindi "B" è il vincitore. Sai cosa significa e come dovrebbe informare la tua strategia CRO?
In questo articolo imparerai i fondamenti della statistica bayesiana che ti aiuteranno a riprendere il controllo dei tuoi test A/B, inclusi
- Una visione imparziale delle statistiche bayesiane
- Vantaggi e svantaggi frequentista vs bayesiano
- La preparazione di cui hai bisogno per interpretare e utilizzare con sicurezza i risultati del test bayesiano A/B evitando alcune trappole di miti comuni.
- Che cos'è la statistica bayesiana?
- La storia delle origini bayesiane
- Un esempio di statistica bayesiana applicata ai test A/B
- Un breve glossario dei termini bayesiani importanti per i tester A/B
- Inferenza bayesiana
- Probabilità condizionale
- Distribuzione di probabilità/Distribuzione di verosimiglianza
- Distribuzione delle credenze precedenti
- Coniugazione
- Priori coniugati
- Funzione di perdita
- Che cos'è la statistica frequentista?
- Test Bayesiano vs Frequentist A/B
- Il quadro frequentista
- Il quadro bayesiano
- Cosa ti dicono effettivamente le statistiche bayesiane nei test A/B?
- Probabilità di essere il migliore (P2BB)
- Aumento previsto
- Perdita prevista
- Miti sulle statistiche bayesiane da evitare
- Mito n. 1: i bayesiani affermano le loro ipotesi, i frequentisti no
- Mito n. 2. I metodi bayesiani ti danno le risposte che desideri davvero
- Mito n. 3: l'inferenza bayesiana ti aiuta a comunicare l'incertezza meglio dell'inferenza frequentista
- Mito #4. I risultati dei test bayesiani A/B sono immuni a sbirciare
- Mito #5. Le statistiche frequentiste sono inefficienti poiché è necessario attendere una dimensione del campione fissa
- Quindi, dovresti scegliere bayesiano o frequentista? C'è un posto per entrambi.
- Chiave da asporto
Pronto? Cominciamo con le basi.
Che cos'è la statistica bayesiana?
La statistica bayesiana è un approccio all'analisi statistica basato sul teorema di Bayes, che aggiorna le convinzioni sugli eventi man mano che vengono raccolti nuovi dati o prove su tali eventi. Qui, la probabilità è una misura della convinzione che si verifichi un evento.
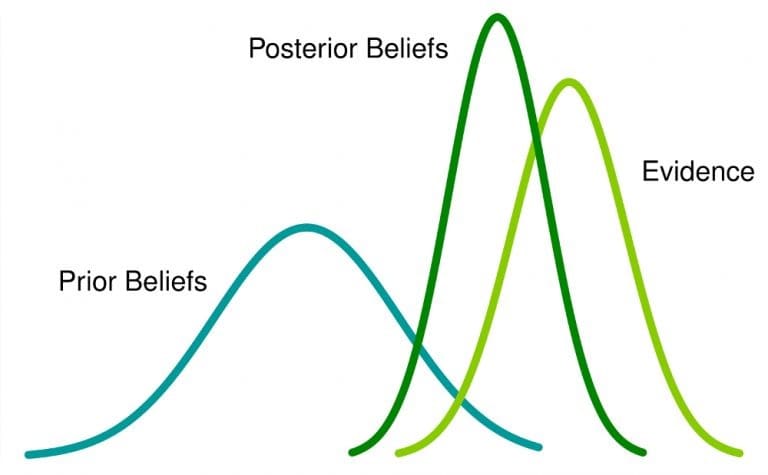
Cosa significa: se hai una convinzione precedente su un evento e ottieni maggiori informazioni ad esso correlate, quella convinzione cambierà (o almeno sarà adattata) a una convinzione successiva.
Ciò è utile per comprendere l'incertezza o quando si lavora con molti dati rumorosi, ad esempio nell'ottimizzazione del tasso di conversione per l'e-commerce e nell'apprendimento automatico.
Immaginiamo questo:
Ad esempio, stai guardando una corsa di carrelli della spesa del college e poi uno spettatore eccitato ti sfida a scommettere che vincerà il tizio con la maglietta rossa che trasporta la signora con la maglietta verde. Ci pensi e rispondi che vinceranno invece il ragazzo con la giacca nera e la ragazza con la felpa nera.

Un altro spettatore sopra la testa e ti ha sussurrato un consiglio: "Il ragazzo con la maglietta rossa ha vinto le ultime 3 gare su 4". Cosa succede alla tua scommessa? Non sei più troppo sicuro, vero?
Supponendo che tu abbia anche saputo che l'ultima volta che il tizio con la giacca nera ha indossato i suoi fortunati occhiali da sole, ha vinto. E le volte in cui non l'ha indossato, ha vinto il ragazzo con la maglietta rossa.
Oggi, vedete che il tizio con la giacca nera indossa quegli occhiali. La tua convinzione cambia di nuovo. Ora hai più fiducia nella tua scommessa, giusto? In questa storia, hai aggiornato la tua convinzione ogni volta che hai avuto prove di nuovi dati. Questo è l'approccio bayesiano.
La storia delle origini bayesiane
Quando il reverendo Thomas Bayes ha pensato per la prima volta alla sua teoria, non pensava che fosse degna di pubblicazione. Quindi, è rimasto nei suoi appunti per oltre un decennio. Fu quando la sua famiglia chiese a Richard Price di esaminare i suoi appunti che Price scoprì le note che costituivano le basi del teorema di Bayes.
È iniziato con un esperimento mentale per Bayes. Pensò di sedersi con le spalle a un tavolo perfettamente piatto e quadrato e di chiedere a un assistente di lanciare una palla sul tavolo.
La palla poteva atterrare ovunque sul tavolo, ma Bayes pensava di poter indovinare dove aggiornando le sue ipotesi con nuove informazioni. Quando la palla è atterrata sul tavolo, ha chiesto all'assistente di dirgli se è atterrata a destra oa sinistra, davanti o dietro al punto in cui era atterrata la palla precedente.
Lo notò e ascoltò mentre altre palline cadevano sul tavolo. Con informazioni aggiuntive come questa, ha scoperto di poter migliorare la precisione delle sue ipotesi ad ogni lancio. Ciò ha portato l'idea di aggiornare la nostra comprensione man mano che acquisivamo più prove dall'osservazione.
L'approccio bayesiano all'analisi dei dati viene applicato in vari campi come la scienza e l'ingegneria e include anche sport e diritto.
Negli esperimenti controllati randomizzati online, in particolare nei test A/B, puoi utilizzare l'approccio bayesiano in 4 passaggi:
- Identifica la tua distribuzione precedente.
- Scegli un modello statistico che rifletta le tue convinzioni.
- Esegui l'esperimento.
- Dopo l'osservazione, aggiorna le tue convinzioni e calcola una distribuzione a posteriori.
Aggiorna le tue convinzioni usando un insieme di regole chiamato algoritmo bayesiano.
Un esempio di statistica bayesiana applicata ai test A/B
Illustriamo un esempio di test bayesiano A/B.
Immagina di aver eseguito un semplice test A/B sul pulsante CTA di un negozio Shopify. Per "A", utilizziamo "Aggiungi al carrello" e per "B", utilizziamo "Aggiungi al carrello".
Ecco come si avvicinerà al test un frequentista.
Esistono due mondi alternativi: uno in cui A e B non sono diversi, quindi il test non mostrerà alcuna differenza nel tasso di conversione. Questa è l'ipotesi nulla. E nell'altro mondo, c'è una differenza, quindi un pulsante funzionerà meglio dell'altro.
Il frequentista presumerà che viviamo nel mondo 1 dove non c'è differenza nei pulsanti CTA, cioè supponendo che l'ipotesi nulla sia vera. E poi cercheranno di dimostrare quell'errore a un livello di certezza predeterminato chiamato livello di significatività.
Ma ecco come un bayesiano si avvicinerà allo stesso test:
Iniziano con una convinzione preliminare che entrambi i pulsanti A e B abbiano le stesse possibilità di produrre un tasso di conversione compreso tra 0 e 100%. Quindi, c'è l'uguaglianza dei pulsanti subito fuori dal cancello: entrambi hanno una probabilità del 50% di essere i migliori.
Quindi inizia il test e vengono raccolti i dati. Dall'osservazione di nuove informazioni, i tester bayesiani A/B aggiorneranno le loro conoscenze. Quindi, se B sta mostrando una promessa, possono raggiungere una convinzione a posteriori basata su quell'osservazione dicendo: "B ha una probabilità del 61% di battere A".
Ci sono differenze fondamentali tra i due metodi.
Ecco perché è importante per noi mantenere un approccio imparziale ai test bayesiani A/B.
La maggior parte degli strumenti di test bayesiani A/B, forse per scopi di marketing, adotta una posizione estrema anti-frequentista e sostiene l'argomento secondo cui il bayesiano è più bravo a dirti quale variante è più "redditizia".
Ma un singolo approccio statistico al test A/B possiede i diritti esclusivi sugli insight?
Se si spinge ulteriormente l'argomento bayesiano, potrebbero trovarsi di fronte a studi in cui gli intervistati affermano di voler sapere qual è la migliore linea d'azione o che vogliono massimizzare i profitti o qualcosa di simile. Questo pone saldamente la domanda nel territorio della teoria delle decisioni - qualcosa in cui né l'inferenza bayesiana né l'inferenza frequentista possono avere voce in capitolo.
Georgi Georgiev, creatore di Analytics-toolkit.com e autore di "Metodi statistici nei test A/B online"
Faremo un breve tuffo in questi dettagli nelle sezioni successive. Per ora, rendiamo il resto di questo primer facile da comprendere.
Un breve glossario dei termini bayesiani importanti per i tester A/B
Inferenza bayesiana
L'inferenza bayesiana sta aggiornando la probabilità di un'ipotesi con nuovi dati. È costruito attorno a credenze e probabilità.
L'inferenza bayesiana sfrutta la probabilità condizionale per aiutarci a capire in che modo i dati influiscono sulle nostre convinzioni. Diciamo che iniziamo con una precedente convinzione che il cielo sia rosso. Dopo aver esaminato alcuni dati, ci rendiamo presto conto che questa convinzione precedente è sbagliata. Quindi, eseguiamo l'aggiornamento bayesiano per migliorare il nostro modello errato sul colore del cielo, finendo con una credenza posteriore più accurata .
Michael Berk in Verso la scienza dei dati
Probabilità condizionale
La probabilità condizionata è la probabilità di un evento dato che si è verificato un altro evento. Cioè, la probabilità di A nella condizione B.
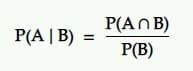
Traduzione: La probabilità che un evento A accada dato un altro evento B è uguale alla probabilità che B e A accadano insieme divisa per la probabilità dell'evento B.
Distribuzione di probabilità/Distribuzione di verosimiglianza
Le distribuzioni di probabilità sono distribuzioni che mostrano quanto è probabile che i tuoi dati assumano un valore specifico.
Laddove i tuoi dati possono assumere più valori, ad esempio una categoria come i colori che potrebbero essere grigio, rosso, arancione, blu, ecc., la tua distribuzione è multinomiale. Per un insieme di numeri, la distribuzione potrebbe essere normale. E per i valori dei dati che potrebbero essere sì/no o vero/falso, sarebbe binomiale.
Distribuzione delle credenze precedenti
Oppure la distribuzione di probabilità a priori, chiamata semplicemente a priori, esprime la tua convinzione prima che tu avessi la prova di nuovi dati. Quindi, è un'espressione della tua convinzione iniziale che aggiornerai dopo aver considerato alcune prove usando l'analisi (o inferenza) bayesiana.
Coniugazione
Prima di tutto, coniugato si riferisce all'essere uniti, di solito in coppia. Nella teoria della probabilità bayesiana, la coniugazione presuppone che il priore sia coniugato alla verosimiglianza.
Se il posteriore ha la stessa forma funzionale del precedente, allora il precedente è coniugato alla funzione di verosimiglianza. Questo mostra come la funzione di verosimiglianza aggiorna la distribuzione precedente.
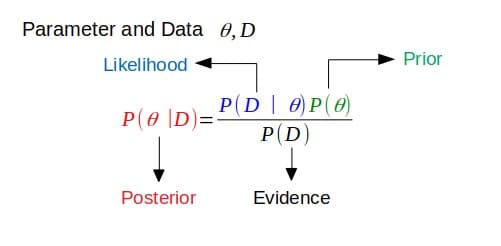
Priori coniugati
Questo è legato alla definizione di cui sopra. Se il posteriore è nella stessa famiglia di distribuzione di probabilità (o ha la stessa forma funzionale) della distribuzione di probabilità precedente, allora il precedente e il posteriore sono distribuzioni coniugate. In questo caso, il priore è chiamato il coniugato per la funzione di verosimiglianza.
Possono essere soggettivi (basati sulla conoscenza dello sperimentatore), oggettivi e informativi (basati su dati storici) o non informativi.
Funzione di perdita
Una funzione di perdita è un modo per quantificare la perdita misurando quanto è pessima la nostra stima attuale. Ci aiuta a ridurre al minimo la perdita per la verifica delle ipotesi, specialmente quando esprimiamo un'inferenza che si trova in un intervallo di valori probabili, e supporta il processo decisionale con i risultati dei nostri test.
Ora che è fuori mano, possiamo andare avanti.
Se sei stato in giro per un po ', probabilmente ti sei imbattuto in più di alcuni meme di statistiche frequentisti e bayesiane.

Entrambe le parti sembrano cercare risposte da direzioni opposte, ma è davvero così? Per capirlo meglio (pur rimanendo imparziali), visitiamo il campo Frequentists.
Che cos'è la statistica frequentista?
Questa è la prima tecnica inferenziale che la maggior parte delle persone impara nelle statistiche. La statistica frequentista calcola la probabilità che un evento (ipotesi) si verifichi frequentemente nelle stesse condizioni.
Il test di ipotesi A/B utilizzando l'approccio frequentista segue questi passaggi:
- Dichiara alcune ipotesi. Tipicamente, l'ipotesi nulla è che la nuova variante “B” non sia migliore dell'originale “A” mentre l'ipotesi alternativa dichiara il contrario.
- Determinare una dimensione del campione in anticipo utilizzando un calcolo statistico della potenza , a meno che non si utilizzino approcci di test sequenziali. Utilizzare un calcolatore della dimensione del campione che consideri la potenza statistica, il tasso di conversione corrente e l'effetto minimo rilevabile.
- Eseguire il test e attendere che ogni variazione sia esposta alla dimensione del campione predeterminata.
- Calcola la probabilità di osservare un risultato almeno tanto estremo quanto i dati sotto l'ipotesi nulla (valore p). Rifiuta l'ipotesi nulla e distribuisci la nuova variante alla produzione se il p-value < 5%.
Come si confronta con il bayesiano? Vediamo…
Test Bayesiano vs Frequentist A/B
Questo è un famigerato dibattito ovunque venga utilizzata l'inferenza statistica. E ad essere sinceri, è inutile. Entrambi hanno i loro pregi e le istanze in cui sono il metodo migliore da usare.
Contrariamente a quanto ti farà pensare la maggior parte dei promotori di entrambi i campi, sono simili in diversi modi e nessuno dei due si avvicina alla verità dell'altro, sebbene i loro approcci siano diversi.
Se applicato al test A/B, ad esempio, nessun metodo specifico ti darà una previsione assoluta e accurata in termini di linea di condotta che causerà la crescita del business. Invece, il test A/B ti aiuta a rimuovere il rischio dal processo decisionale.
Indipendentemente da come analizzi i tuoi dati, utilizzando approcci bayesiani o frequentisti, puoi muoverti con un certo livello di certezza che hai ragione.
E per questo motivo, entrambi i modelli statistici sono validi. Il bayesiano può avere un vantaggio in termini di velocità ma è più impegnativo dal punto di vista computazionale del frequentista.
Scopri altre differenze...
Il quadro frequentista
La maggior parte di noi ha familiarità con l'approccio frequentista dai corsi introduttivi di statistica. Abbiamo definito la metodologia sopra: dalla dichiarazione dell'ipotesi nulla, alla determinazione della dimensione del campione, alla raccolta di dati tramite un esperimento randomizzato e infine all'osservazione di un risultato statisticamente significativo.
Nel frequentismo, consideriamo la probabilità come fondamentalmente correlata alle frequenze degli eventi ripetuti. Quindi, in un lancio di monete equo, un frequentista crede che se indovina abbastanza frequentemente, otterrà testa nel 50% delle volte e lo stesso per croce.
Mentalità frequentista: "Se ripeto l'esperimento nelle stesse condizioni più e più volte, quali sono le possibilità che il mio metodo ottenga la risposta giusta?"
Il quadro bayesiano
Mentre l'approccio frequentista tratta il parametro della popolazione per ciascuna variante come una costante (sconosciuta), l'approccio bayesiano modella ogni valore di parametro come una variabile casuale con una certa distribuzione di probabilità.
Qui si calcolano direttamente le distribuzioni di probabilità (e quindi i valori attesi) per i parametri di interesse.
E per modellare la distribuzione di probabilità per ciascuna variante, ci basiamo sulla regola di Bayes per combinare i risultati dell'esperimento con qualsiasi conoscenza precedente che abbiamo sulla metrica di interesse. Possiamo semplificare i calcoli usando un coniugato a priori.
Alex Birkett ha riassunto l'algoritmo bayesiano in questo modo:
- Definisci la distribuzione a priori che incorpora le tue convinzioni soggettive su un parametro. Il priore può essere non informativo o informativo.
- Raccogliere dati.
- Aggiorna la tua distribuzione precedente con i dati usando il teorema di Bayes (sebbene tu possa avere metodi bayesiani senza l'uso esplicito della regola di Bayes, vedi bayesiano non parametrico) per ottenere una distribuzione a posteriori. La distribuzione a posteriori è una distribuzione di probabilità che rappresenta le tue convinzioni aggiornate sul parametro dopo aver visto i dati.
- Analizzare la distribuzione a posteriori e riassumerla (media, mediana, sd, quantili...).
In breve, lo sperimentatore bayesiano si concentra sulla propria prospettiva e su cosa significa per loro la probabilità. La loro opinione si evolve con i dati osservati. I frequentisti, d'altra parte, credono che la risposta giusta sia là fuori da qualche parte.

Comprendi che il dibattito frequentista vs bayesiano non ha un grande impatto sull'analisi dei test A/B post. Le principali differenze tra i due campi sono più legate a ciò che può essere testato.
Le statistiche di probabilità non sono generalmente utilizzate in larga misura nelle analisi successive. L'argomento bayesiano-frequentista è più applicabile per quanto riguarda la scelta delle variabili da testare nel paradigma A/B, ma anche lì la maggior parte dei tester A/B viola l'inferno di ipotesi di ricerca, probabilità e intervalli di confidenza .
Il dottor Rob Balon a CXL
Georgi elabora ulteriormente:
Esistono più calcolatori bayesiani online e almeno un importante fornitore di software di test A/B che applica un motore statistico bayesiano che utilizzano tutti i cosiddetti priori non informativi (un nome un po' improprio, ma non approfondiamo questo aspetto). Nella maggior parte dei casi i risultati di questi strumenti coincidono numericamente con i risultati di un test frequentista sugli stessi dati. Diciamo che lo strumento bayesiano riporterà qualcosa come "96% di probabilità che B sia migliore di A" mentre lo strumento frequentista produrrà un p-value di 0,04 che corrisponde a un livello di confidenza del 96%.
In una situazione come quella sopra, che è molto più comune di quanto alcuni vorrebbero ammettere, entrambi i metodi porteranno alla stessa inferenza e il livello di incertezza sarà lo stesso, anche se l'interpretazione è diversa.
Cosa direbbe un bayesiano di questo risultato? Trasforma il valore p in una probabilità a posteriori adeguata quando si visualizza uno scenario in cui non ci sono informazioni preliminari? O tutte queste applicazioni dei test bayesiani sono fuorvianti per l'utilizzo di un priore non informativo di per sé?
Non c'è davvero bisogno di scegliere un campo e trovare un posto dietro un riparo per lanciare pietre contro l'altro campo. Ci sono anche prove che entrambi i framework producono gli stessi risultati. Indipendentemente dalla strada che scegli, la destinazione sarà probabilmente la stessa. Dipende da come puoi arrivarci con Frequentist vs Bayesiano.
Per esempio:
- Ci sono dati che mostrano che i test bayesiani sono più veloci e la scelta preferita per esperimenti interattivi:
Poiché il paradigma bayesiano consente agli sperimentatori di quantificare formalmente le credenze e incorporare conoscenze aggiuntive, è più veloce dell'analisi statistica tradizionale.
In una simulazione di test bayesiano A/B, quando il criterio di decisione è stato aggiustato (cioè aumentando la tolleranza agli errori), il 75% degli esperimenti si è concluso entro il 22,7% delle osservazioni richieste dall'approccio tradizionale (a un livello di significatività del 5%). E ha registrato solo il 10% di errore di tipo II. - Il bayesiano è anche considerato più indulgente, mentre il frequentista è avverso al rischio:
Mentre molti test frequentisti utilizzano una significatività statistica del 95%, i bayesiani possono accontentarsi di meno. Se una variante ha una probabilità del 78% di battere il controllo, a seconda della perdita prevista, potrebbe essere una buona decisione distribuire quella variante.
Se ti sbagli e la perdita prevista è inferiore all'uno per cento, questo è un danno piuttosto insignificante per molte aziende. Questo approccio scadente potrebbe essere più adatto a un rapido processo decisionale in scenari a rischio molto basso. - Tuttavia, le simulazioni e i calcoli bayesiani sono pesanti in termini di calcolo:
Frequentist, d'altra parte, è basato su carta e penna. Avvertenza: se il tuo strumento di test A/B utilizza il bayesiano e non sai quali ipotesi vengono aggiunte ai tuoi dati, non puoi fare affidamento sulla "risposta" fornita dal tuo fornitore. Prendetela con un pizzico di sale. Ed esegui la tua analisi.
Non è tutto sole e arcobaleni con il bayesiano. Come sottolinea Georgi con questo elenco di domande:
- "Vuoi ottenere il prodotto della probabilità a priori e della funzione di verosimiglianza?"
- "Vuoi la combinazione di probabilità a priori e dati come output?"
- "Vuoi che le convinzioni soggettive mescolate ai dati producano l'output?" (se si utilizzano a priori informativi)
- "Ti sentiresti a tuo agio nel presentare statistiche in cui ci sono informazioni preliminari che si presume siano altamente certe mescolate con i dati effettivi?"
Questi sono tutti aspetti della statistica bayesiana, in parole povere.
Cosa ti dicono effettivamente le statistiche bayesiane nei test A/B?
Hai progettato il tuo test A/B per fornire informazioni dettagliate su come una modifica influisce sulla tua metrica di interesse, come il tasso di conversione o le entrate per visitatore.
Quando usi uno strumento che funziona con le statistiche bayesiane, è importante capire cosa significano i tuoi risultati perché "B è il vincitore" non significa esattamente ciò che la maggior parte delle persone pensa che significhi.
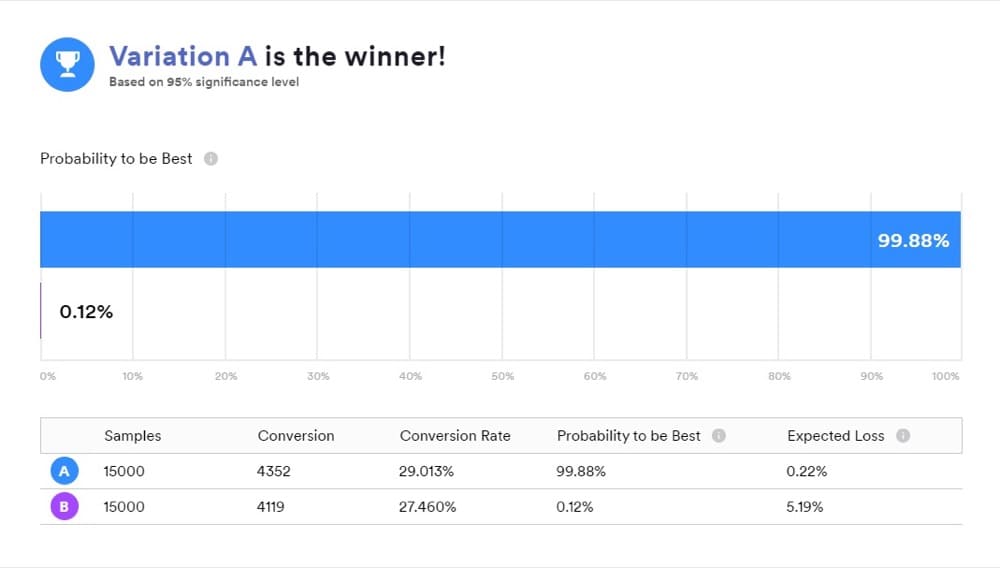
È un modo conveniente per presentare i risultati, ma non è quello che ha rivelato il tuo test. Invece, le risposte che vuoi sono nei confronti posteriori di "A" e "B".
Ecco i 3 metodi di confronto:
Probabilità di essere il migliore (P2BB)
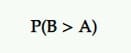
Questa è la probabilità che dichiari un vincitore nel test bayesiano A/B.
La variante con la probabilità di essere la migliore è quella con la più alta probabilità di continuare a sovraperformare l'altra.
Questo viene calcolato da una serie di campioni posteriori della misura di interesse dall'originale e dallo sfidante.
Quindi, se B ha la più alta probabilità di aumentare i tuoi tassi di conversione, ad esempio, B viene dichiarato vincitore.
Aumento previsto
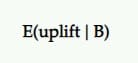
Quindi, se B è il vincitore, quanto rialzo dovremmo aspettarci da esso? Continuerebbe a fornire gli stessi risultati che abbiamo visto nel test?
Questa è l'intuizione che l'aumento atteso cerca di fornire. L'aumento atteso della scelta di B su A, dato un insieme di campioni posteriori, è definito come l'intervallo credibile (o media) dell'aumento percentuale.
Nei test A/B, di solito lo confrontiamo come sfidante con il controllo. Quindi, se lo sfidante ha perso, è rappresentato in valori negativi (come -11,35%) e valori positivi (come +9,58%) se ha vinto.
Perdita prevista
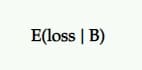
Dal momento che non c'è una probabilità del 100% che B sia migliore di A, allora c'è la possibilità di registrare una perdita se si sceglie B su A. Questa è rappresentata come perdita attesa e, proprio come con un aumento atteso, è espressa dal punto di vista dello sfidante contro il controllo.
Ti dice il rischio di scegliere la tua variante P2BB (cioè il vincitore dichiarato).
Prima di addentrarci nei miti, un enorme ringraziamento alla leggenda dell'analitica Georgi Georgiev. Le sue analisi approfondite dell'inferenza frequentista vs bayesiana e delle probabilità e statistiche bayesiane nei test A/B hanno ispirato la sezione successiva.
Miti sulle statistiche bayesiane da evitare
Con una rivalità vecchia quasi quanto inutile, il dibattito bayesiano vs frequentista ha raccolto molti input e "ha dato origine a molti miti.
Il più grande di questi miti (mito n. 2) è promosso dai fornitori di strumenti di test A/B per dirti perché un approccio è migliore dell'altro.
Ma dopo aver letto le sezioni precedenti, lo sai meglio.
Riveliamo i buchi in questi miti.
Mito n. 1: i bayesiani affermano le loro ipotesi, i frequentisti no
Ciò suggerisce che i bayesiani fanno ipotesi sotto forma di distribuzioni a priori e queste sono aperte per la valutazione. Ma i frequentisti fanno ipotesi nascoste nel bel mezzo della matematica.
Perché è sbagliato: bayesiani e frequentisti fanno ipotesi di fondo simili, l'unica differenza è che i bayesiani fanno ipotesi aggiuntive, oltre alla matematica.
I modelli frequentisti utilizzano ipotesi in matematica, come la forma della distribuzione, l'omogeneità o l'eterogeneità dell'effetto tra le osservazioni e l'indipendenza dell'osservazione. E non sono nascosti. In effetti, sono ampiamente discussi nella comunità statistica e dichiarati per ogni test statistico frequentista.
La verità: i frequentisti dichiarano esplicitamente le loro ipotesi e fanno un ulteriore passo avanti per testare le ipotesi: test di normalità, test di bontà dell'adattamento (in base al quale abbiamo il test di disadattamento del rapporto di campionamento) e altro ancora.
Mito n. 2. I metodi bayesiani ti danno le risposte che desideri davvero
L'idea sbagliata qui è che i valori p e gli intervalli di confidenza non dicono ai tester ciò che vogliono sapere, mentre le probabilità a posteriori e gli intervalli credibili lo fanno. La gente vuole sapere cose come
- La probabilità che B superi A e
- La probabilità che il risultato non sia una coincidenza.
I valori P e i test di ipotesi (inferenza diretta) non forniscono tali informazioni, ma l'inferenza inversa lo fa.
Perché è sbagliato: questa è una questione di linguistica. In genere, quando i non statistici usano termini come "probabilità", "caso" e "probabilità", non li usano tenendo conto del loro significato tecnico. Sonda più a fondo e scoprirai che sono confusi tanto sull'inferenza inversa quanto sull'inferenza diretta.
Secondo Georgi Georgiev, iniziano a sorgere domande come queste:
- “ Che cos'è una probabilità a priori? Che valore porta?"
- "Cos'è una funzione di verosimiglianza?"
- "Quale probabilità 'precedente', non ho dati precedenti?"
- "Come faccio a difendere la scelta di una probabilità a priori?"
- "C'è un modo per comunicare esattamente ciò che dicono i dati, senza nessuna di queste miscele?"
La verità: ci dovrebbe essere una migliore comprensione di ciò che i tester vogliono sapere, non sulla loro errata interpretazione dei termini tecnici. I valori P, gli intervalli di confidenza e altri ti dicono quanto sono ben sondati i risultati con i dati raccolti. Hanno fornito una misura di certezza senza l'influenza di ipotesi precedenti soggettive e non verificate.
Mito n. 3: l'inferenza bayesiana ti aiuta a comunicare l'incertezza meglio dell'inferenza frequentista
Perché i risultati dei test producono approfondimenti più “significativi”.
Perché è sbagliato: sia l'approccio frequentista che quello bayesiano hanno strumenti simili per aiutarti a comunicare la certezza e i risultati del tuo test A/B.
| Frequentista | bayesiano | ||||||||||
| ● Stime puntuali | ● Stime puntuali | ||||||||||
| ● Valori P | ● Intervalli credibili | ||||||||||
| ● Intervalli di confidenza | ● Fattori di Bayes | ||||||||||
| ● Curve del valore P | ● Distribuzioni posteriori (svolgere lo stesso compito come le curve frequentiste) | ||||||||||
| ● Curve di fiducia | |||||||||||
| ● Curve di gravità, ecc. |
La verità: tutto dipende da come li usi. Entrambi i metodi sono ugualmente efficaci nel comunicare l'incertezza. Tuttavia, ci sono differenze nel modo in cui presentano la misura dell'incertezza.
Mito #4. I risultati dei test bayesiani A/B sono immuni a sbirciare
Alcuni statistici bayesiani sostengono puoi interrompere un test bayesiano una volta che vedi un "vincente chiaro" e fa poca differenza per il risultato finale.
Probabilmente sai che questo è inaccettabile nei test frequentisti, quindi è considerato uno svantaggio rispetto al bayesiano. Ma lo è davvero?
Perché è sbagliato: in uno studio del 1969 sul Journal of the Royal Statistical Society intitolato “Repeated Significance Tests on Accumulating Data”, Armitage et al. ha mostrato come l'arresto opzionale basato sui risultati aumenti la probabilità di errore.
Non puoi semplicemente fermarti quando noti un vincitore, aggiornare il tuo posteriore e usarlo come tuo prossimo precedente senza modificare il modo in cui funziona l'analisi bayesiana.
La verità: sbirciare influenza l'inferenza bayesiana tanto quanto fa frequentista (se vuoi farlo bene).
Mito #5. Le statistiche frequentiste sono inefficienti poiché è necessario attendere una dimensione del campione fissa
Alcuni membri della comunità CRO ritengono che i test statistici frequentisti debbano essere eseguiti con una dimensione del campione fissa e predeterminata, altrimenti i risultati non sono validi.
Di conseguenza, aspetti più del necessario per ottenere i risultati desiderati.
Perché è sbagliato: le statistiche frequentiste non vengono utilizzate in questo modo da circa sette decenni. Con i test sequenziali frequentisti non è necessaria una durata predeterminata fissa.
La verità: i test sequenziali, che sono più popolari oggi, richiedono una dimensione massima del campione per bilanciare gli errori di tipo I e di tipo II, ma la dimensione effettiva del campione utilizzata varia da caso a caso a seconda del risultato osservato.
Quindi, dovresti scegliere bayesiano o frequentista? C'è un posto per entrambi.
Non c'è bisogno di scegliere da che parte stare. Entrambi i metodi hanno il loro posto. Ad esempio, un progetto a lungo termine che utilizza priori aggiornati e necessita di risultati rapidi si adatta meglio all'approccio bayesiano.
Il metodo frequentista, d'altra parte, è più adatto per progetti che richiedono una notevole ripetibilità nei loro risultati. Come per la scrittura di software che utilizzeranno molte persone con molti set di dati.
Come afferma Cassie Kozyrkov, Head of Decision Intelligence di Google, "La statistica è la scienza per cambiare idea nell'incertezza".
Nel suo video di riepilogo delle statistiche bayesiane e frequentiste, ha detto:
“Puoi prendere quel dibattito frequentista e bayesiano e far crollare tutto su ciò su cui stai cambiando idea. I frequentisti cambiano idea sulle azioni, hanno un'azione predefinita preferita - forse non hanno alcuna convinzione - ma hanno un'azione che gli piace sotto ignoranza e poi chiedono: "Le mie prove [o dati] cambiano idea su quell'azione?" "Mi sento ridicolo a farlo sulla base delle mie prove?"
I bayesiani, d'altra parte, cambiano idea in un modo diverso. Iniziano con un'opinione, un'opinione personale espressa matematicamente, chiamata a priori, e poi chiedono: "Qual è l'opinione sensata che dovrei avere dopo aver incorporato alcune prove?" E così i frequentisti cambiano idea sulle azioni, i bayesiani cambiano idea sulle credenze.
E a seconda di come vuoi inquadrare il tuo processo decisionale, potresti preferire andare con un campo piuttosto che con l'altro. "
Alla fine, ci stiamo dirigendo tutti verso conclusioni simili: la differenza è nel modo in cui tali conclusioni ti vengono presentate.
Se l'inferenza frequentista e bayesiana fossero funzioni di programmazione, con gli input che sono problemi statistici, le due sarebbero diverse in ciò che restituiscono all'utente. La funzione di inferenza frequentista restituirebbe un numero, che rappresenta una stima (tipicamente una statistica riassuntiva come la media campionaria ecc.), mentre la funzione bayesiana restituirebbe le probabilità.
Estratto dal libro “Programmazione probabilistica e metodi bayesiani per hacker
Ciò che non è del tutto corretto è l'affermazione che uno dia risultati più pratici dell'altro.
Chiave da asporto
La statistica bayesiana nei test A/B consiste in 4 fasi distinte:
- Identifica la tua distribuzione precedente
- Scegli un modello statistico che rifletta le tue convinzioni
- Esegui l'esperimento
- Usa i risultati per aggiornare le tue convinzioni e calcolare una distribuzione a posteriori
I tuoi risultati ti indirizzeranno verso probabilità perspicaci. Quindi saprai quale variante ha la più alta probabilità di essere la migliore, la tua perdita prevista e il tuo aumento previsto.
Questi sono generalmente interpretati per te dalla maggior parte degli strumenti di test A/B utilizzando le statistiche bayesiane. Ma uno sperimentatore approfondito eseguirà un'analisi post-test per comprendere meglio quei risultati.
Poiché sei arrivato così lontano, ecco un fatto divertente per te: conosci il ritratto di Thomas Bayes che tutti conoscono? Questo:

Nessuno è sicuro al 100% che sia lui.