Kesalahan Tipe I dan Tipe II: Kesalahan yang Tak Terelakkan dalam Pengoptimalan

Kesalahan tipe I dan tipe II terjadi ketika Anda salah menemukan pemenang dalam eksperimen Anda atau gagal menemukannya. Dengan kedua kesalahan, Anda akhirnya pergi dengan apa yang tampaknya berhasil atau tidak. Dan tidak dengan hasil yang sebenarnya.

Salah menafsirkan hasil pengujian tidak hanya mengakibatkan upaya pengoptimalan yang salah arah, tetapi juga dapat menggagalkan program pengoptimalan Anda dalam jangka panjang.

Waktu terbaik untuk mengetahui kesalahan ini adalah bahkan sebelum Anda membuatnya! Jadi, mari kita lihat bagaimana Anda dapat menghindari kesalahan tipe I dan tipe II dalam eksperimen pengoptimalan Anda.

Tapi sebelum itu, mari kita lihat hipotesis nolnya… karena penolakan atau tidak penolakan yang salah dari hipotesis nollah yang menyebabkan kesalahan tipe I dan tipe II .

Hipotesis Null: H0

Saat Anda menghipotesiskan eksperimen, Anda tidak langsung menyarankan bahwa perubahan yang diusulkan akan memindahkan metrik tertentu.

Anda mulai dengan mengatakan bahwa perubahan yang diusulkan tidak akan memengaruhi metrik terkait sama sekali — bahwa perubahan tersebut tidak terkait.

Ini adalah hipotesis nol Anda (H0). H0 selalu tidak ada perubahan. Inilah yang Anda yakini, secara default… sampai (dan jika) eksperimen Anda menyangkalnya.

Dan hipotesis alternatif Anda (Ha atau H1) adalah bahwa ada perubahan positif. H0 dan Ha selalu berlawanan secara matematis. Ha adalah salah satu di mana Anda mengharapkan perubahan yang diusulkan untuk membuat perbedaan, ini adalah hipotesis alternatif Anda — dan inilah yang Anda uji dengan eksperimen Anda.

Jadi, misalnya, jika Anda ingin menjalankan eksperimen di halaman penetapan harga dan menambahkan metode pembayaran lain ke dalamnya, pertama-tama Anda harus membuat hipotesis nol yang mengatakan: Metode pembayaran tambahan tidak akan berdampak pada penjualan. Hipotesis alternatif Anda akan berbunyi: Metode pembayaran tambahan AKAN meningkatkan penjualan.

Menjalankan eksperimen, pada kenyataannya, menantang hipotesis nol atau status quo.

Kesalahan tipe I dan tipe II terjadi ketika Anda salah menolak atau gagal menolak hipotesis nol.

Memahami Kesalahan Tipe I

Kesalahan tipe I dikenal sebagai kesalahan positif palsu atau kesalahan Alpha.

Dalam contoh kesalahan tipe I pengujian hipotesis, pengujian atau eksperimen pengoptimalan Anda * TAMPAKNYA BERHASIL* dan Anda (secara keliru) menyimpulkan bahwa variasi yang Anda uji berbeda (lebih baik atau lebih buruk) dari aslinya.

Pada kesalahan tipe I, Anda melihat kenaikan atau penurunan — yang hanya sementara dan kemungkinan tidak akan bertahan dalam jangka panjang — dan akhirnya menolak hipotesis nol Anda (dan menerima hipotesis alternatif Anda).

Menolak hipotesis nol secara keliru dapat terjadi karena berbagai alasan, tetapi yang utama adalah praktik mengintip (yaitu, melihat hasil Anda untuk sementara atau saat eksperimen masih berjalan). Dan memanggil tes lebih cepat dari kriteria penghentian yang ditetapkan tercapai.

Banyak metodologi pengujian mencegah praktik mengintip karena melihat hasil sementara dapat menyebabkan kesimpulan yang salah yang mengakibatkan kesalahan tipe I.

Inilah cara Anda dapat membuat kesalahan tipe I:

Misalkan Anda mengoptimalkan halaman arahan situs web B2B Anda dan berhipotesis bahwa menambahkan lencana atau penghargaan ke dalamnya akan mengurangi kecemasan prospek Anda, sehingga meningkatkan rasio pengisian formulir Anda (menghasilkan lebih banyak prospek).

Jadi hipotesis nol Anda untuk eksperimen ini menjadi: Menambahkan lencana tidak berdampak pada pengisian formulir.

Kriteria penghentian untuk eksperimen semacam itu biasanya adalah periode tertentu dan/atau setelah konversi X terjadi pada tingkat signifikansi statistik yang ditetapkan. Secara konvensional, pengoptimal mencoba mencapai tanda kepercayaan statistik 95% karena memberi Anda peluang 5% untuk membuat kesalahan tipe I yang dianggap cukup rendah untuk sebagian besar eksperimen pengoptimalan. Secara umum, semakin tinggi metrik ini, semakin rendah kemungkinan membuat kesalahan tipe I.

Tingkat kepercayaan yang Anda tuju menentukan berapa probabilitas Anda untuk mendapatkan kesalahan tipe I (α).

Jadi jika Anda menargetkan tingkat kepercayaan 95%, nilai Anda untuk menjadi 5%. Di sini, Anda menerima bahwa ada kemungkinan 5% bahwa kesimpulan Anda bisa salah.

Sebaliknya, jika Anda menggunakan tingkat kepercayaan 99% dengan eksperimen Anda, kemungkinan Anda mendapatkan kesalahan tipe I turun menjadi 1%.

Katakanlah, untuk eksperimen ini, Anda menjadi terlalu tidak sabar dan alih-alih menunggu eksperimen berakhir, Anda melihat dasbor alat pengujian Anda (intip!) hanya sehari. Dan Anda melihat peningkatan "nyata" — bahwa rasio pengisian formulir Anda telah meningkat sebesar 29,2% dengan tingkat kepercayaan 95%.

Dan BAM…

… Anda menghentikan eksperimen Anda.

… tolak hipotesis nol (bahwa lencana tidak berdampak pada penjualan).

… menerima hipotesis alternatif (bahwa lencana meningkatkan penjualan).

… dan jalankan dengan versi dengan lencana penghargaan.

Tetapi ketika Anda mengukur prospek Anda selama sebulan, Anda menemukan jumlahnya hampir sebanding dengan apa yang Anda laporkan dengan versi aslinya. Lagi pula, lencana itu tidak terlalu penting. Dan bahwa hipotesis nol mungkin ditolak dengan sia-sia.

Apa yang terjadi di sini adalah Anda mengakhiri eksperimen terlalu cepat dan menolak hipotesis nol dan berakhir dengan pemenang yang salah — membuat kesalahan tipe I.

Menghindari Kesalahan Tipe I dalam Eksperimen Anda

Salah satu cara pasti untuk menurunkan peluang Anda untuk mencapai kesalahan tipe I adalah dengan tingkat kepercayaan yang lebih tinggi. Tingkat signifikansi statistik 5% (diterjemahkan ke tingkat kepercayaan statistik 95%) dapat diterima. Ini adalah taruhan yang akan dilakukan oleh sebagian besar pengoptimal dengan aman karena, di sini, Anda akan gagal dalam kisaran 5% yang tidak mungkin.

Selain menetapkan tingkat kepercayaan yang tinggi, menjalankan tes Anda cukup lama adalah penting. Kalkulator durasi pengujian dapat memberi tahu Anda berapa lama Anda harus menjalankan pengujian (setelah mempertimbangkan hal-hal seperti ukuran efek yang ditentukan antara lain). Jika Anda membiarkan eksperimen berjalan sesuai tujuannya, Anda secara signifikan mengurangi peluang menemukan kesalahan tipe 1 (mengingat Anda menggunakan tingkat kepercayaan yang tinggi). Menunggu hingga Anda mencapai hasil yang signifikan secara statistik memastikan bahwa hanya ada kemungkinan kecil (biasanya 5%) bahwa Anda salah menolak hipotesis nol dan melakukan kesalahan tipe I. Dengan kata lain, gunakan ukuran sampel yang baik karena itu penting untuk mendapatkan hasil yang signifikan secara statistik.

Nah, itu semua tentang kesalahan tipe I yang terkait dengan tingkat kepercayaan (atau signifikansi) dalam eksperimen Anda. Tetapi ada juga jenis kesalahan lain yang dapat menyusup ke dalam pengujian Anda — kesalahan tipe II.

Memahami Kesalahan Tipe II

Kesalahan tipe II dikenal sebagai negatif palsu atau kesalahan Beta.

Berbeda dengan kesalahan tipe I, dalam contoh kesalahan tipe II, percobaan *TAMPAKNYA TIDAK BERHASIL (ATAU TIDAK MENYUKAI)* dan Anda (secara keliru) menyimpulkan bahwa variasi yang Anda uji tidak berbeda dari asli.

Dalam kesalahan tipe II, Anda gagal melihat kenaikan atau penurunan yang sebenarnya dan akhirnya gagal menolak hipotesis nol dan menolak hipotesis alternatif.

Inilah cara Anda membuat kesalahan tipe II:

Kembali ke situs B2B yang sama dari atas…

Jadi misalkan kali ini Anda berhipotesis bahwa menambahkan penafian kepatuhan GDPR secara mencolok di bagian atas formulir Anda akan mendorong lebih banyak prospek untuk mengisinya (menghasilkan lebih banyak prospek).

Oleh karena itu, hipotesis nol Anda untuk eksperimen ini menjadi: Penafian kepatuhan GDPR tidak memengaruhi pengisian formulir.

Dan hipotesis alternatif untuk hal yang sama berbunyi: Penafian kepatuhan GDPR menghasilkan lebih banyak pengisian formulir.

Kekuatan statistik tes menentukan seberapa baik tes dapat mendeteksi perbedaan kinerja versi asli dan versi penantang Anda, jika ada penyimpangan. Secara tradisional, pengoptimal mencoba mencapai tanda kekuatan statistik 80% karena semakin tinggi metrik ini, semakin rendah kemungkinan membuat kesalahan tipe II.

Daya statistik mengambil nilai antara 0 dan 1 (dan sering dinyatakan dalam %) dan mengontrol kemungkinan kesalahan tipe II Anda (β); itu dihitung sebagai: 1 –

Semakin tinggi kekuatan statistik pengujian Anda, semakin rendah kemungkinan menemukan kesalahan tipe II.

Jadi, jika sebuah eksperimen memiliki kekuatan statistik 10%, maka eksperimen tersebut bisa sangat rentan terhadap kesalahan tipe II. Padahal, jika sebuah eksperimen memiliki kekuatan statistik 80%, kemungkinannya akan membuat kesalahan tipe II jauh lebih kecil.

Sekali lagi, Anda menjalankan pengujian, tetapi kali ini Anda tidak melihat peningkatan signifikan dalam pengisian formulir Anda. Kedua versi melaporkan konversi yang hampir serupa. Karena itu, Anda menghentikan eksperimen dan melanjutkan dengan versi asli tanpa penafian kepatuhan GDPR.

Namun, saat Anda menggali lebih dalam data prospek dari periode eksperimen, Anda menemukan bahwa meskipun jumlah prospek dari kedua versi (asli dan penantang) tampak identik, versi GDPR memang memberi Anda peningkatan yang baik dan signifikan dalam jumlah lead dari Eropa. (Tentu saja, Anda dapat menggunakan penargetan pemirsa untuk menampilkan eksperimen hanya kepada prospek dari Eropa – tetapi itu cerita lain.)

Apa yang terjadi di sini adalah Anda mengakhiri tes Anda terlalu dini, tanpa memeriksa apakah Anda telah mencapai kekuatan yang cukup — membuat kesalahan tipe II.

Menghindari Kesalahan Tipe II dalam Eksperimen Anda

Untuk menghindari kesalahan tipe II, jalankan pengujian dengan kekuatan statistik tinggi. Cobalah untuk mengonfigurasi eksperimen Anda sehingga Anda dapat mencapai setidaknya tanda kekuatan statistik 80%. Ini adalah tingkat kekuatan statistik yang dapat diterima untuk sebagian besar eksperimen pengoptimalan. Dengan itu, Anda dapat memastikan bahwa dalam 80% kasus, setidaknya, Anda akan menolak hipotesis nol palsu dengan benar.

Untuk melakukan ini, Anda perlu melihat faktor-faktor yang menambahnya.

Yang terbesar adalah ukuran sampel (mengingat ukuran efek yang diamati). Ukuran sampel terkait langsung dengan kekuatan tes. Ukuran sampel yang besar berarti uji daya tinggi. Tes yang kurang bertenaga sangat rentan terhadap kesalahan tipe II karena peluang Anda untuk mendeteksi perbedaan hasil penantang Anda dan versi asli sangat berkurang, terutama untuk MEI rendah (lebih lanjut tentang ini di bawah). Jadi untuk menghindari kesalahan tipe II, tunggu pengujian mengumpulkan daya yang cukup untuk meminimalkan kesalahan tipe II. Idealnya, untuk sebagian besar kasus, Anda ingin mencapai kekuatan minimal 80%.

Faktor lainnya adalah Minimum Effect of Interest (MEI) yang Anda targetkan untuk eksperimen Anda. MEI (juga disebut MDE) adalah besaran minimum dari perbedaan yang ingin Anda deteksi dalam KPI yang bersangkutan. Jika Anda menetapkan MEI rendah (mengincar peningkatan 1,5%, misalnya), peluang Anda untuk menemukan kesalahan tipe II meningkat karena mendeteksi perbedaan kecil membutuhkan ukuran sampel yang jauh lebih besar (untuk mencapai daya yang cukup).

Dan akhirnya, penting untuk dicatat bahwa cenderung ada hubungan terbalik antara probabilitas membuat kesalahan tipe I (α) dan kemungkinan membuat kesalahan tipe II (β). Misalnya, jika Anda menurunkan nilai untuk menurunkan kemungkinan membuat kesalahan tipe I (misalnya Anda menetapkan pada 1%, yang berarti tingkat kepercayaan 99%), kekuatan statistik eksperimen Anda (atau kemampuannya, , mendeteksi perbedaan ketika ada) akhirnya berkurang juga, sehingga meningkatkan kemungkinan Anda mendapatkan kesalahan tipe II.

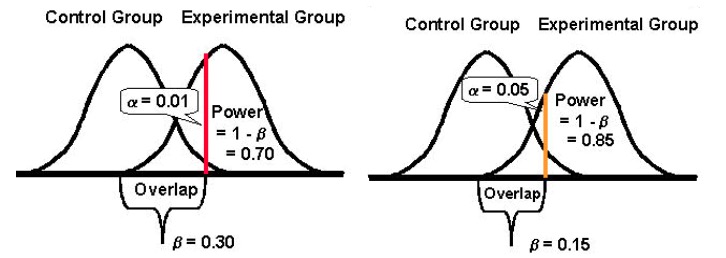
Menjadi Lebih Menerima Salah Satu Kesalahan: Tipe I dan II (& Menyeimbangkan)

Menurunkan kemungkinan satu jenis kesalahan meningkatkan jenis lainnya (mengingat semua yang lain tetap sama).

Jadi, Anda perlu menerima panggilan tentang jenis kesalahan apa yang bisa lebih Anda tolerir.

Membuat kesalahan tipe I, di satu sisi, dan meluncurkan perubahan untuk semua pengguna Anda dapat membebani Anda dengan konversi dan pendapatan — lebih buruk lagi, bisa menjadi pembunuh konversi juga.

Membuat kesalahan tipe II, di sisi lain, dan gagal meluncurkan versi pemenang untuk semua pengguna Anda dapat, sekali lagi, membebani Anda dengan konversi yang seharusnya Anda menangkan.

Selalu, kedua kesalahan datang dengan biaya.

Namun, bergantung pada eksperimen Anda, yang satu mungkin lebih dapat Anda terima daripada yang lain. Secara umum, penguji menemukan kesalahan tipe I sekitar empat kali lebih serius daripada kesalahan tipe II .

Jika Anda ingin mengambil pendekatan yang lebih seimbang, ahli statistik Jacob Cohen menyarankan Anda harus menggunakan kekuatan statistik 80% yang datang dengan “ keseimbangan yang wajar antara risiko alfa dan beta. ” (daya 80% juga merupakan standar untuk sebagian besar alat pengujian.)

Dan sejauh signifikansi statistik yang bersangkutan, standar ditetapkan pada 95%.

Pada dasarnya, ini semua tentang kompromi dan tingkat risiko yang ingin Anda toleransi. Jika Anda ingin benar-benar meminimalkan kemungkinan kedua kesalahan tersebut, Anda dapat memilih tingkat kepercayaan 99% dan kekuatan 99%. Tapi itu berarti Anda akan bekerja dengan ukuran sampel yang sangat besar untuk periode yang tampak sangat lama. Selain itu, bahkan saat itu Anda akan meninggalkan beberapa ruang untuk kesalahan.

Sesekali, Anda AKAN menyimpulkan eksperimen salah. Tapi itu bagian dari proses pengujian — butuh beberapa saat untuk menguasai statistik pengujian A/B. Menyelidiki dan menguji ulang atau menindaklanjuti eksperimen Anda yang berhasil atau gagal adalah salah satu cara untuk menegaskan kembali temuan Anda atau menemukan bahwa Anda melakukan kesalahan.