Jaringan Saraf Neuron Tunggal dengan Python – Dengan Intuisi Matematika

Mari kita bangun jaringan sederhana — sangat sangat sederhana, tetapi jaringan lengkap — dengan satu lapisan. Hanya satu input — dan satu neuron (yang juga merupakan output), satu bobot, satu bias.

Mari kita jalankan kodenya terlebih dahulu dan kemudian menganalisis bagian demi bagian

Kloning proyek Github, atau cukup jalankan kode berikut di IDE favorit Anda.

Jika Anda memerlukan bantuan dalam menyiapkan IDE, saya menjelaskan prosesnya di sini.

Jika semuanya berjalan baik-baik saja, Anda akan mendapatkan output ini:

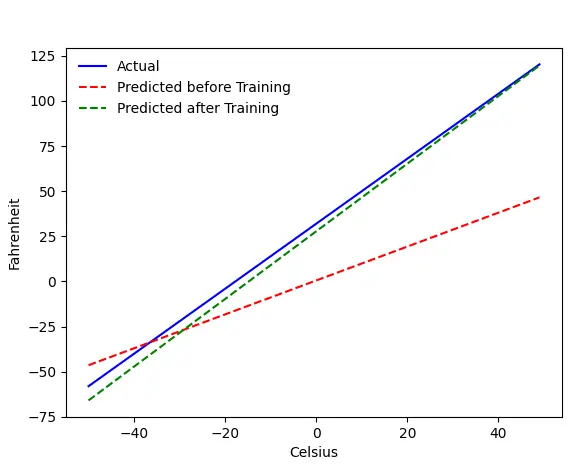
Masalahnya — Fahrenheit dari Celsius

Kami akan melatih mesin kami untuk memprediksi Fahrenheit dari Celcius. Seperti yang dapat Anda pahami dari kode (atau grafik), garis biru adalah hubungan Celsius-Fahrenheit yang sebenarnya. Garis merah adalah hubungan yang diprediksi oleh mesin bayi kita tanpa pelatihan apa pun. Akhirnya, kami melatih mesin, dan garis hijau adalah prediksi setelah pelatihan.

Lihat Baris#65–67 — sebelum dan sesudah pelatihan, ini memprediksi menggunakan fungsi yang sama ( get_predicted_fahrenheit_values() ). Jadi apa yang dilakukan kereta ajaib()? Mari kita cari tahu.

Struktur Jaringan

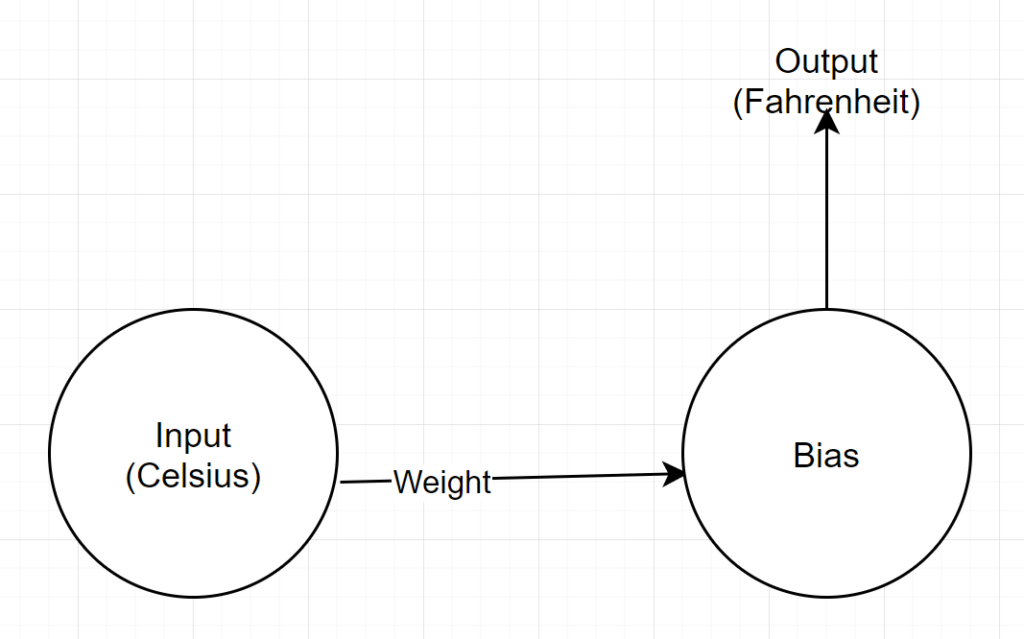
Input: Angka yang mewakili celcius

Berat: Pelampung yang mewakili berat

Bias: Pelampung yang mewakili bias

Output: Pelampung yang mewakili prediksi Fahrenheit

Jadi, kami memiliki total 2 parameter — 1 bobot dan 1 bias

Analisis Kode

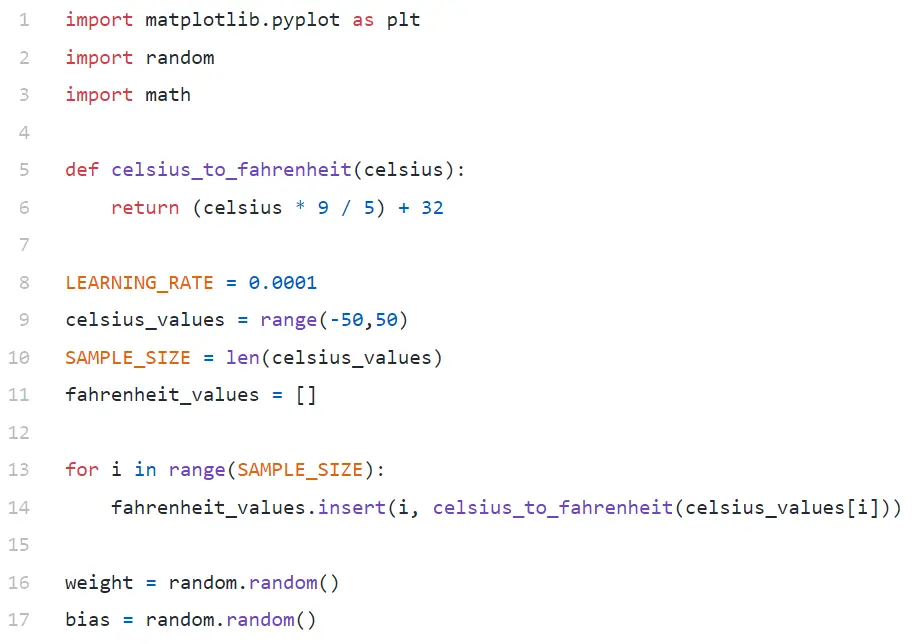
Di Baris#9, kami membuat larik 100 angka antara -50 dan +50 (tidak termasuk 50 — fungsi rentang mengecualikan nilai batas atas).

Di Baris#11–14, kami menghasilkan Fahrenheit untuk setiap nilai celsius.

Pada baris#16 dan #17, kami menginisialisasi bobot dan bias.

kereta()

Kami menjalankan 10.000 iterasi pelatihan di sini. Setiap iterasi dibuat dari:

1. meneruskan (Baris#57) lulus
2. mundur (Baris#58) lulus
3. update_parameters (Baris#59)

Jika Anda baru mengenal python, mungkin terlihat agak aneh bagi Anda — fungsi python dapat mengembalikan beberapa nilai sebagai Tuple .

Perhatikan bahwa update_parameters adalah satu-satunya hal yang kami minati. Semua hal lain yang kami lakukan di sini adalah mengevaluasi parameter fungsi ini, yang merupakan gradien (kami akan menjelaskan di bawah apa itu gradien) dari bobot dan bias kami.

1. grad_weight: Pelampung yang mewakili gradien berat
2. grad_bias: Pelampung yang mewakili gradien bias

Kami mendapatkan nilai-nilai ini dengan memanggil mundur, tetapi membutuhkan output, yang kami dapatkan dengan memanggil maju di baris#57.

maju()

Perhatikan bahwa di sini celsius_values ​​dan fahrenheit_values ​​adalah array dari 100 baris:

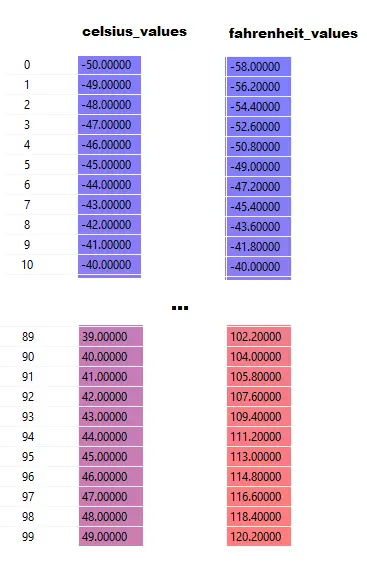
Setelah mengeksekusi Baris#20–23, untuk nilai celsius, katakanlah 42

keluaran = 42 * berat + bias

Jadi, untuk 100 elemen dalam celsius_values ​​, output akan berupa larik 100 elemen untuk setiap nilai celsius yang sesuai.

Baris#25–30 menghitung kerugian menggunakan fungsi kerugian Mean Squared Error (MSE), yang hanya merupakan nama indah dari kuadrat semua perbedaan dibagi dengan jumlah sampel (dalam hal ini 100).

Kerugian kecil berarti prediksi yang lebih baik. Jika Anda terus mencetak kerugian di setiap iterasi, Anda akan melihat bahwa itu berkurang saat pelatihan berlangsung.

Akhirnya, di Baris#31 kami mengembalikan prediksi keluaran dan kerugian.

ke belakang

Kami hanya tertarik untuk memperbarui bobot dan bias kami. Untuk memperbarui nilai-nilai itu, kita harus mengetahui gradiennya, dan itulah yang kita hitung di sini.

Gradien pemberitahuan sedang dihitung dalam urutan terbalik. Gradien keluaran dihitung terlebih dahulu, kemudian untuk bobot dan bias, dan kemudian diberi nama "propagasi balik". Pasalnya, untuk menghitung gradien bobot dan bias, kita perlu mengetahui gradien keluaran — agar bisa digunakan dalam rumus aturan rantai .

Sekarang mari kita lihat apa itu gradien dan aturan rantai.

gradien

Demi kesederhanaan, pertimbangkan kami hanya memiliki satu nilai celsius_values ​​dan fahrenheit_values ​​, 42 dan 107,6 masing-masing.

Nah, rincian perhitungan pada Baris#30 menjadi:

rugi = (107,6 — (42 * berat + bias))² / 1

Seperti yang Anda lihat, kerugian bergantung pada 2 parameter — bobot dan bias. Pertimbangkan beratnya. Bayangkan, kita menginisialisasinya dengan nilai acak, katakanlah, 0,8, dan setelah mengevaluasi persamaan di atas, kita mendapatkan 123,45 sebagai nilai loss . Berdasarkan nilai kerugian ini, Anda harus memutuskan bagaimana Anda akan memperbarui berat badan. Haruskah Anda membuatnya 0,9, atau 0,7?

Anda harus memperbarui bobot sedemikian rupa sehingga pada iterasi berikutnya Anda mendapatkan nilai kerugian yang lebih rendah (ingat, meminimalkan kerugian adalah tujuan akhir). Jadi, jika menambah berat badan meningkatkan penurunan, kami akan menurunkannya. Dan jika peningkatan berat badan menurunkan penurunan, kami akan meningkatkannya.

Sekarang, pertanyaannya, bagaimana kita tahu apakah peningkatan bobot akan menambah atau mengurangi kerugian. Di sinilah gradien masuk . Secara garis besar, gradien didefinisikan oleh turunan. Ingat dari kalkulus SMA Anda, y/x (yang merupakan turunan parsial/gradien y terhadap x) menunjukkan bagaimana y akan berubah dengan perubahan kecil pada x.

Jika y/∂x positif, berarti kenaikan kecil pada x akan meningkatkan y.

Jika y/∂x negatif, berarti kenaikan kecil pada x akan menurunkan y.

Jika y/∂x besar, perubahan kecil pada x akan menyebabkan perubahan besar pada y.

Jika y/∂x kecil, perubahan kecil pada x akan menyebabkan perubahan kecil pada y.

Jadi, dari gradien, kami mendapatkan 2 informasi. Ke arah mana parameter harus diperbarui (naik atau turun) dan berapa banyak (besar atau kecil).

Aturan Rantai

Secara informal, aturan rantai mengatakan:

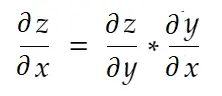
Perhatikan contoh berat di atas. Kita perlu menghitung grad_weight untuk memperbarui bobot ini, yang akan dihitung dengan:

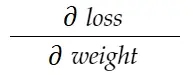
Dengan rumus aturan rantai, kita dapat menurunkannya:

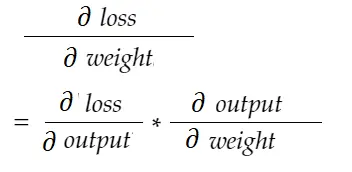
Demikian pula, gradien untuk bias:

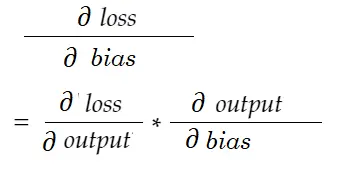
Mari kita menggambar diagram ketergantungan.

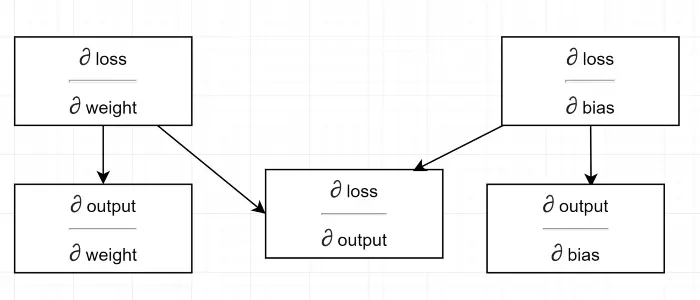
Lihat semua perhitungan tergantung pada gradien output (∂ loss/∂ output) . Makanya kita hitung dulu di backpass (Baris#34–36).

Faktanya, dalam kerangka kerja ML tingkat tinggi, misalnya di PyTorch, Anda tidak perlu menulis kode untuk backpass! Selama lintasan maju, ia membuat grafik komputasi, dan selama lintasan mundur, ia melewati arah yang berlawanan dalam grafik dan menghitung gradien menggunakan aturan rantai.

rugi / keluaran

Kami mendefinisikan variabel ini dengan grad_output dalam kode, yang kami hitung pada Baris#34–36. Mari cari tahu alasan di balik rumus yang kita gunakan dalam kode.

Ingat, kita memberi makan semua 100 celsius_values ​​di mesin bersama-sama. Jadi, grad_output akan menjadi larik 100 elemen, setiap elemen berisi gradien output untuk elemen yang sesuai dalam celsius_values ​​. Untuk mempermudah, mari kita pertimbangkan, hanya ada 2 item dalam celsius_values ​​.

Jadi, meruntuhkan baris#30,

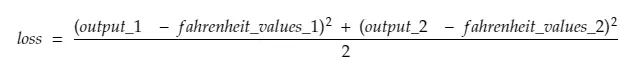
di mana,

output_1 = nilai keluaran untuk nilai celsius pertama

output_2 = nilai keluaran untuk nilai celsius ke-2

fahreinheit_values_1 = Nilai fahreinheit sebenarnya untuk nilai celsius pertama

fahreinheit_values_1 = Nilai fahreinheit aktual untuk nilai celsius ke-2

Sekarang, variabel yang dihasilkan grad_output akan berisi 2 nilai — gradien dari output_1 dan output_2, artinya:

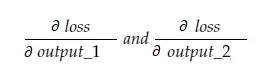
Mari kita menghitung gradien output_1 saja, dan kemudian kita dapat menerapkan aturan yang sama untuk yang lain.

Waktu kalkulus!

Yang sama dengan baris#34–36.

Gradien berat

Bayangkan, kita hanya memiliki satu elemen dalam celsius_values. Sekarang:

Yang sama dengan Baris#38–40. Untuk 100 nilai_celsius, nilai gradien untuk setiap nilai akan dijumlahkan. Pertanyaan yang jelas adalah mengapa kita tidak memperkecil hasilnya (yaitu membagi dengan SAMPLE_SIZE). Karena kita mengalikan semua gradien dengan faktor kecil sebelum memperbarui parameter, itu tidak perlu (lihat bagian terakhir Memperbarui Parameter).

Gradien bias

Yang sama dengan Baris#42. Seperti gradien bobot, nilai-nilai ini untuk masing-masing dari 100 input diringkas. Sekali lagi, tidak apa-apa karena gradien dikalikan dengan faktor kecil sebelum memperbarui parameter.

Memperbarui Parameter

Akhirnya, kami memperbarui parameter. Perhatikan bahwa gradien dikalikan dengan faktor kecil (LEARNING_RATE) sebelum dikurangi, untuk membuat pelatihan stabil. Nilai LEARNING_RATE yang besar akan menyebabkan masalah overshooting dan nilai yang sangat kecil akan membuat pelatihan lebih lambat, yang mungkin memerlukan lebih banyak iterasi. Kita harus menemukan nilai optimal untuk itu dengan beberapa coba-coba. Ada banyak sumber online di dalamnya termasuk yang ini untuk mengetahui lebih banyak tentang Learning Rate.

Perhatikan bahwa, jumlah pasti yang kami sesuaikan tidak terlalu penting. Misalnya, jika Anda menyetel LEARNING_RATE sedikit, variabel keturunan_gradasi_berat dan keturunan_grad_bias (Baris#49–50) akan diubah, tetapi mesin mungkin masih berfungsi. Yang penting adalah memastikan jumlah ini diturunkan dengan memperkecil gradien dengan faktor yang sama (LEARNING_RATE dalam kasus ini). Dengan kata lain, "menjaga penurunan gradien proporsional" lebih penting daripada "berapa banyak penurunannya ".

Perhatikan juga bahwa nilai gradien ini sebenarnya adalah jumlah gradien yang dievaluasi untuk masing-masing dari 100 input. Tetapi karena ini diskalakan dengan nilai yang sama, tidak apa-apa seperti yang disebutkan di atas.

Untuk memperbarui parameter, kita harus mendeklarasikannya dengan kata kunci global (di Baris#47).

Ke mana harus pergi dari sini?

Kode akan jauh lebih kecil dengan mengganti loop for dengan pemahaman daftar dengan cara Pythonic. Lihat sekarang — tidak perlu lebih dari beberapa menit untuk memahaminya.

Jika Anda memahami semuanya sejauh ini, mungkin ini saat yang tepat untuk melihat bagian dalam jaringan sederhana dengan banyak neuron/lapisan — inilah artikelnya.