Distribusi Normal – Pengenalan Intuitif Tanpa Matematika

Saya akan mencoba untuk menjaga artikel ini bebas dari persamaan dan jargon suap — sebanyak mungkin. Saya, bagaimanapun, membutuhkan Anda untuk setidaknya memiliki kemampuan berikut:

• Mampu menginterpretasikan grafik sederhana.
• Pengetahuan tingkat dasar dalam probabilitas. Anda setidaknya mengerti bahwa ada kemungkinan 50% untuk kepala jika saya melempar koin.
• Kalkulus integral dan fisika kuantum (bercanda!)

Mengapa Distribusi Normal

Cara intuitif untuk memahami sesuatu adalah dengan menyelidiki mengapa hal itu diperlukan. Mari kita lakukan untuk distribusi normal (juga disebut, Distribusi Gaussian).

Katakanlah Anda memiliki kebiasaan lucu. Setiap hari Anda melempar koin 100 kali. Adalah "normal" untuk mengharapkan bahwa Anda akan mendapatkan kepala 50 kali - atau hampir 50 kali hampir sepanjang hari. Jarang, ada hari-hari baik untuk kepala — Anda mungkin mendapatkan sekitar 55 kali, dan sangat jarang di atas 65 kali.

Sekarang, Anda ingin mengukur "kelangkaan" ini. Jadi, Anda mulai mencatat berapa kali Anda mendapatkan kepala setiap hari.

Jumlah kepala setiap hari dalam setahun

Di bawah ini adalah data setelah satu tahun (365 hari) — yang pertama adalah jumlah kepala yang Anda dapatkan pada hari pertama, dan yang terakhir adalah jumlah kepala yang Anda dapatkan pada hari terakhir. Anda tidak perlu memeriksa semua angka di bawah ini, tetapi mudah untuk mengetahui bahwa kebanyakan dari mereka adalah sekitar 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Visualisasikan Lebih Baik dengan Histogram

Mari kita plot histogram dari data di atas:

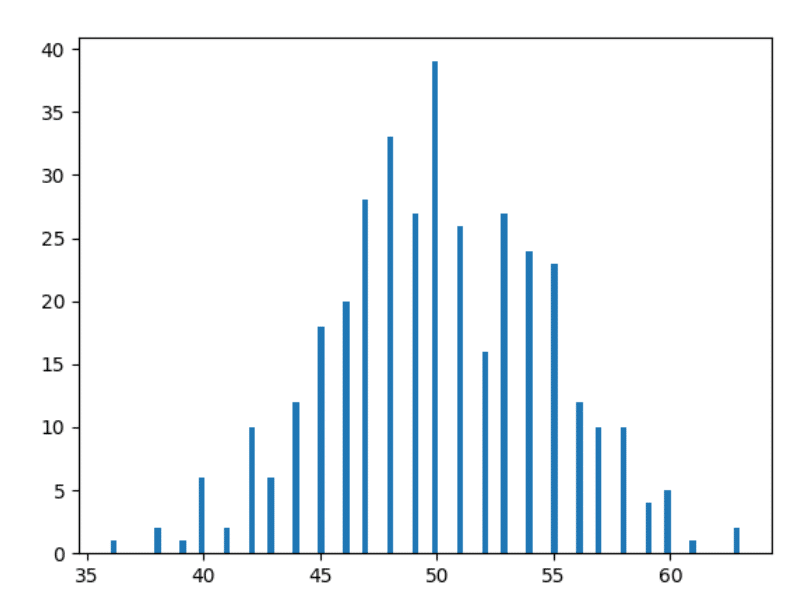
Ah! Bukankah itu sudah terlihat seperti gambar yang Anda lihat di internet ketika Anda googling "Distribusi Normal"? Kami hampir sampai!

Jadi, jika Anda tidak mengerti histogram - kami baru saja merencanakan di sini jumlah hari kami mendapat hitungan tertentu untuk kepala. Misalnya, kita mendapat kepala 36 kali pada 2 hari tertentu dalam setahun (periksa data di atas jika Anda tidak percaya), itulah sebabnya ada batang dengan ketinggian 2 satuan pada titik horizontal di 36 (merah persegi panjang di sebelah kiri pada gambar di bawah).

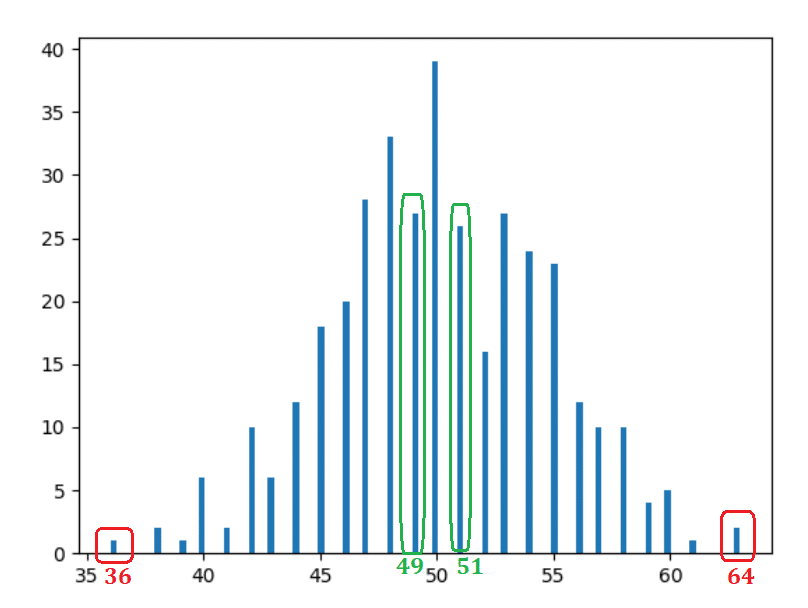
Pengamatan

1. Cukup jelas dan diharapkan — 50 kepala sering terjadi.
2. Semakin jauh dari pusat (50), kejadiannya semakin berkurang.
3. Batang pada jarak yang sama mengambil bentuk yang serupa. Misalnya, jika Anda memindahkan satu unit ke kiri (49) atau kanan (51) — kemunculannya serupa — masing-masing 30 dan 31 (persegi panjang hijau). Jika Anda memindahkan 14 unit ke kiri (36) atau ke kanan (64), kemunculannya serupa lagi — masing-masing 2 dan 1 (persegi panjang merah).

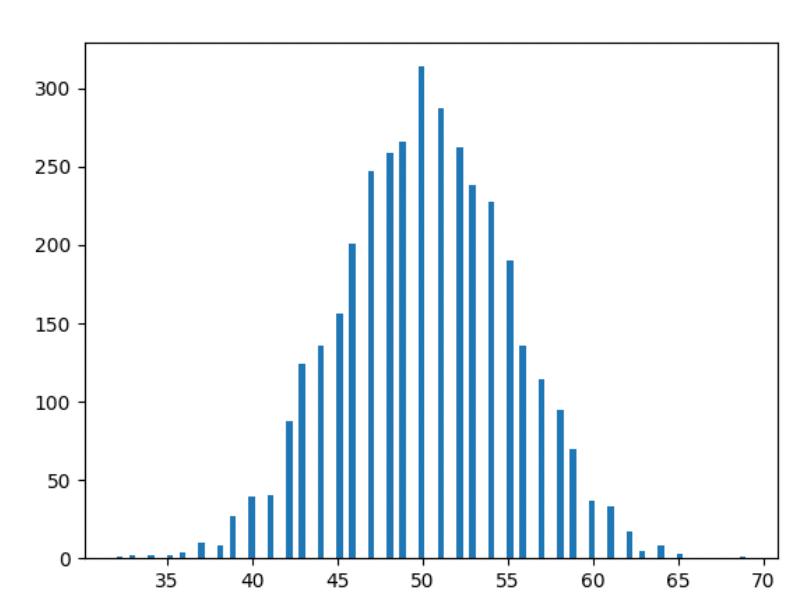
data 10 tahun

Sekarang mari kita maju sedikit — dan memplot data 10 tahun.

data 1000 tahun

Oke — yang terakhir. Mari kita plot data 1000 tahun.

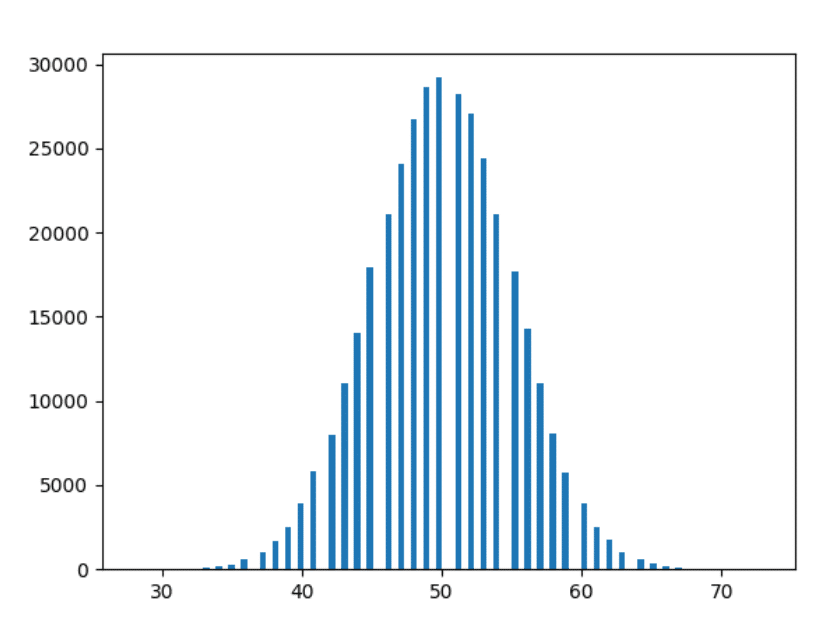
Pengamatan

1. Semakin banyak kita bereksperimen, semakin halus bentuknya.
2. Semakin banyak kami bereksperimen, semakin banyak batang mengikuti pengamatan di atas (yaitu batang pada jarak yang sama mengambil bentuk yang lebih dekat).

Di mana distribusi normal sialan itu?

Oke — terlalu banyak latar belakang — sekarang mari kita langsung ke intinya.

Mari kita lihat jawaban yang disarankan oleh Google:

Beberapa hal dalam definisi ini:

Variabel Acak: Sederhananya — variabel acak adalah sekumpulan nilai yang mungkin dari eksperimen acak seperti lemparan koin. Dalam contoh kita, nilai yang mungkin dari eksperimen kita adalah Head atau Tail .

Berbentuk Lonceng: Apakah Anda memperhatikan bahwa histogram kita berbentuk lonceng?

Simetris: Batang pada jarak yang sama memiliki bentuk yang serupa — bukankah itu simetris?

Jadi, distribusi normal mewakili distribusi hasil untuk peristiwa seperti lemparan koin — di mana distribusi cenderung mempertahankan beberapa properti, termasuk simetri dan bentuk lonceng.

Fenomena apa selain lemparan koin yang mengikuti distribusi normal?

Beberapa contoh keren di sini.

• Tinggi dalam populasi — lebih banyak orang termasuk dalam kelompok tinggi rata-rata. Sangat jarang menemukan orang yang sangat tinggi atau sangat pendek. Dan kemungkinan menemukan sangat tinggi dan sangat pendek hampir sama.
• Melempar dadu
• Ukuran sepatu
• IQ
• Dan masih banyak lainnya…

Apakah fenomena ini secara ketat mengikuti distribusi normal?

Jawaban sederhananya adalah tidak. Meskipun, seperti yang kita lihat di atas — semakin banyak Anda bereksperimen, semakin banyak data yang akan mengikuti sifat distribusi normal. Tetapi tidak ada jaminan bahwa beberapa peristiwa yang tidak mungkin tidak akan terjadi.

Apakah semua distribusi probabilitas di alam semesta berdistribusi normal?

Tidak. Ada banyak fenomena yang ditentukan oleh beberapa jenis distribusi lain.

• Probabilitas kedatangan sejumlah pelanggan tertentu, panggilan telepon, kecelakaan, acara olahraga, dan banjir mengikuti Distribusi Poisson .
• Untuk penjualan bisnis, 20% pelanggan perusahaan bertanggung jawab atas 80% penjualan. ( Distribusi Pareto )
• Pola lalu lintas di kota — Distribusi Eksponensial
• Pemilihan acak anggota untuk tim dari populasi anak perempuan dan laki-laki — Distribusi Hipergeometrik

Dan masih banyak lagi …

Saya membuat daftar di atas hanya dengan googling "contoh kehidupan nyata" dengan beberapa distribusi yang tercantum di sini — bukan berarti saya memahami semuanya.

Apakah ada alasan mengapa beberapa fenomena alam cenderung mengikuti distribusi normal?

Ya — mengutip penjelasan favorit saya:

Penjelasan biasa diberikan dengan nama lain untuk distribusi normal, yaitu “distribusi kesalahan”. Idenya adalah bahwa kesalahan umumnya acak, sehingga kemungkinan besar mengarah ke satu arah seperti ke arah lain. Misalnya, penembak jitu cenderung menembak sedikit ke kiri, sedikit ke kanan, atau sedikit tinggi sedikit rendah. Dengan demikian, grafik seberapa jauh tembakan dari sasaran akan mencerminkan kecenderungan acak ini, dan menjadi simetris di sekitar mean. Demikian pula, dengan tinggi badan dan kecerdasan — banyak gen (mungkin ribuan) berkontribusi pada hasil ini, seperti halnya sejumlah besar faktor lingkungan, seperti nutrisi, penyakit, pendapatan rendah, dan sebagainya.

Parameter distribusi normal

Jika Anda memiliki intuisi dari diskusi sejauh ini — Anda sudah menjadi pemenangnya. Misi selesai. Sisa artikel adalah bonus.

Semua grafik distribusi normal yang Anda lihat berbeda bentuknya. Beberapa dari mereka lebih datar daripada yang lain. Beberapa dari mereka memiliki ketinggian yang baik. Semua bentuk ini dikendalikan hanya oleh 2 parameter:

Berarti

Mean didefinisikan oleh rata-rata. Ini menentukan ketinggian bel. Untuk contoh lemparan koin, rata-ratanya mendekati 50, yang merupakan lokasi teratas dalam grafik.

Standar Deviasi

Karena saya berjanji artikel ini akan bebas dari persamaan, saya tidak memberikan representasi matematisnya di sini. Tapi itu tidak terlalu sulit. Standar deviasi adalah metrik untuk mewakili seberapa beragam data.

Misalnya, standar deviasi usia di penitipan anak akan lebih rendah daripada standar deviasi usia di klub penggemar sepak bola, karena perbedaan usia antara kelompok termuda dan tertua seharusnya jauh lebih tinggi di klub penggemar sepak bola.

Standar deviasi menentukan lebar kurva. Standar deviasi yang kecil menghasilkan kurva yang curam, dan standar deviasi yang lebih besar menghasilkan kurva yang lebih datar.