Rasakan Kalkulus Dengan Sense Pemrograman Anda

Saya percaya orang yang bisa membuat kode — memiliki kemampuan untuk memahami konsep yang lebih rumit daripada kalkulus. Salah satu alasan mengapa ada banyak programmer berbakat di luar sana yang masih berjuang dengan kalkulus bukanlah karena sulit. Hal ini sebagian besar karena kita telah diajarkan dengan cara yang salah (bersama dengan banyak topik lainnya).

Jika Anda telah melakukan beberapa pengkodean dalam hidup Anda — bahkan beberapa latihan mainan seperti menghasilkan bilangan prima, Anda mungkin telah melakukan hal serupa yang terjadi dalam kalkulus tetapi tidak pernah memiliki kesempatan untuk menghubungkannya.

Tujuan penulisan ini bukan untuk mengajari Anda kalkulus atau pemrograman — tetapi untuk membantu Anda menghubungkan beberapa titik.

Saya akan sampai ke bagian pengkodean dalam satu menit. Tetapi izinkan saya untuk memberikan beberapa latar belakang singkat sebelum itu.

Tingkat Perubahan

Kalkulus diferensial berbicara tentang "laju perubahan". Mari kita coba memahami apa artinya itu.

Untuk perubahan variabel (x), laju perubahan fungsi hanyalah perubahan fungsi dibagi dengan perubahan x. Biarkan visualisasikan dengan angka aktual:

Pertimbangkan 2 titik x=2 dan x=6, dan fungsi y=f(x) = x².

Juga, pertimbangkan dx = jarak antara 2 titik ini dalam sumbu x. Dan dy adalah jarak antara nilai y untuk nilai x ini.

Maka, laju perubahan y dari x=2 ke x=6 adalah

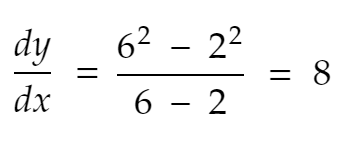
Turunan

Sekarang — turunan dy/dx adalah laju perubahan y untuk perubahan x yang sangat kecil. Karena jarak ini (6–2=4) tidak sangat kecil — bahkan tidak dekat, kita tidak dapat menyebut persamaan di atas sebagai turunan. Jadi, mari kita pilih angka yang lebih kecil, 0,1, untuk saat ini.

Ketika x = 0, y = x² = 0² = 0.

Tetangga terdekat ke arah positif, x = 0,1. Di sana y menjadi 0,1² = 0,01.

Jadi,

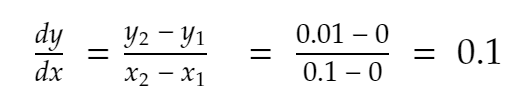
Mari kita coba sekali lagi. Tetangga terdekat 0,1 ke arah positif, x = 0,2. Jadi, y menjadi 0,2² = 0,04. Jadi,

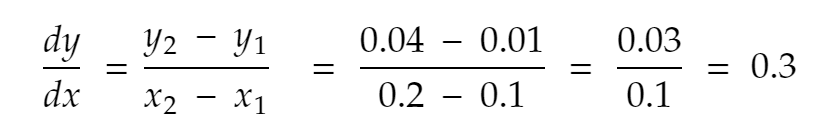
Jika kita ulangi prosesnya beberapa kali lagi, inilah yang kita dapatkan:

Ini file excelnya jika Anda ingin memainkannya.

dx (yang merupakan jarak fiksi yang sangat kecil antara 2 titik yang berdekatan pada sumbu x) adalah 0,1 dalam konteks kita.

x meningkat sesuai.

y hanyalah x².

dy adalah jarak antara 2 nilai y yang berdekatan. Misalnya, ketika x= 0,1, jarak antara arus y (0,01 ) dan y berikutnya (0,04) adalah 0,03 — jadi, dy adalah 0,03 pada x=0,1.

dy/dx adalah dy dibagi dx.

dy/dx / x adalah dy/dx dibagi dengan x.

Sekarang perhatikan bahwa, ketika x bertambah, baris terakhir mendekati 2, yang berarti — laju perubahan x² terhadap x mendekati dua kali x, yaitu 2x .

Ingat turunan x² terhadap x? 2x! Menemukan beberapa koneksi?

Waktu Pengkodean

Mari kita coba hal-hal dalam kode yang telah kita bahas selama ini.

Dengan asumsi Anda sudah menginstal Python, di terminal, jalankan:

Setelah itu, jalankan kode Python berikut:

Di Sini:

x : berisi angka dari 0 sampai 9.

y : array lain, setiap elemen adalah kuadrat dari elemen x yang sesuai

dy : Array lain diinisialisasi dengan nol. Kami akan menempatkan y-jarak dalam array ini.

dydx : Array lain diinisialisasi dengan nol. Ini akan berisi nilai dy/dx dari setiap titik.

dx : Cukup jelas — ini adalah ukuran langkah. Jarak antara 2 angka berurutan, yang berkurang saat SIZE meningkat. Jika UKURAN = 10, dx = 1. Jika UKURAN = 100, dx = 0,1.

Pertama, kita menurunkan dy untuk setiap titik. Kemudian kami menghitung dydx darinya.

Perhatikan itu:

Di sini kita menghilangkan nilai pertama dan terakhir. Nilai pertama x adalah 0, yang akan menghasilkan kesalahan pembagian nol. Dan kita tidak dapat menghitung nilai terakhir dari dy/dx karena kita tidak memiliki nilai terakhir dari dy — karena itu akan membutuhkan di sebelah nilai y terakhir yang tersedia, yang tidak kita miliki di sini.

Jika semuanya berjalan dengan baik, Anda akan mendapatkan grafik ini:

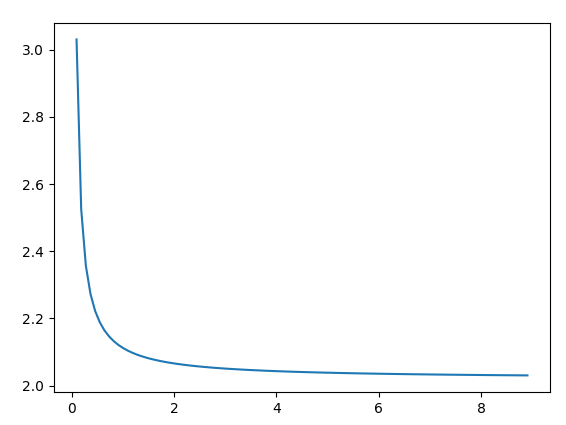
Apa yang Anda pahami dari plot?

Seperti yang Anda lihat, grafik mendekati 2. Tingkatkan nilai SIZE (artinya pengaturan lebih rendah dari dx) dan lihat bagaimana grafik lebih cepat mendekati 2.

Turunan Kedua

Sekarang Anda telah sampai sejauh ini, hanya beberapa langkah lagi untuk mewujudkan turunan kedua, yang akan memberi Anda intuisi untuk turunan dari urutan apa pun.

Seperti yang Anda ingat, turunan kedua adalah laju perubahan turunan pertama terhadap x. Sederhananya — dy/dx pada turunan kedua seperti y pada turunan pertama.

Mari kita lakukan modifikasi berikut pada kode di atas:

Deklarasikan 2 array lagi:

d2ydx2 : Yang akan mewakili turunan kedua:

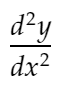
distance_dydx: Untuk mewakili jarak antara nilai dy/dx antara 2 titik yang berdekatan

Berikut adalah kode lengkap untuk turunan kedua:

Setelah menghitung dydx dalam for loop, kita mengeksekusi loop lain untuk menghitung turunan kedua. Dengan beberapa pengkodean yang bijak, kita dapat menghitung turunan kedua dalam loop yang sama (coba sebagai latihan) —tetapi saya memisahkannya di sini untuk kejelasan.

Juga, perhatikan bahwa:

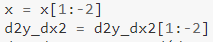
Seperti yang kami lakukan di turunan pertama, kami juga menghilangkan beberapa nilai di sini. 2 nilai terakhir dihilangkan karena yang kedua dari yang terakhir akan membutuhkan nilai "turunan pertama" terakhir, yang tidak dapat kami hitung (karena kami tidak memiliki nilai y yang diperlukan untuk itu — seperti dijelaskan di atas). Apakah itu berarti kita harus menghilangkan 3 nilai terakhir dalam kasus turunan ke-3?🤔 — itu untuk Anda temukan.

Berikut grafik keluarannya:

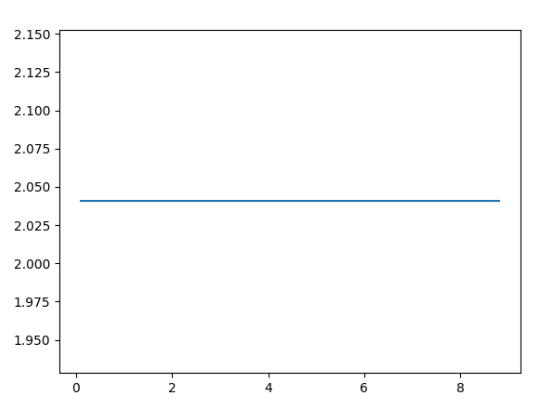
Apa yang kita lihat di sini?

Seperti yang Anda ketahui dari sekolah menengah:

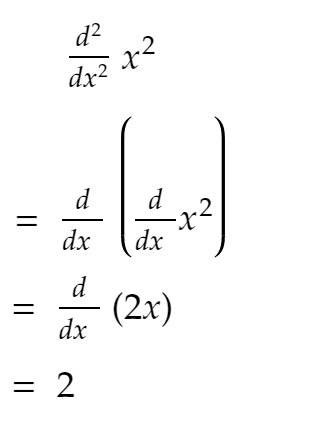
Sekarang, seperti yang Anda lihat dari kode di atas, turunan kedua sebagian besar tetap konstan, dan jika Anda terus meningkatkan SIZE — mendekati 2!

Mengapa tingkat perubahan itu penting

Anda mungkin bertanya-tanya:

— Mengapa kita bisa melewati semua masalah buruk ini? Informasi bermanfaat apa yang kita peroleh dari laju perubahan atau turunannya?

— Mengapa kita tidak bisa mengikuti tingkat perubahan untuk jumlah berapa pun? Mengapa hanya sangat kecil? Informasi apa yang kita peroleh dari laju perubahan terhadap nilai yang sangat kecil , yang tidak dapat ditemukan dari laju perubahan terhadap nilai yang lebih besar?

— Hal yang sangat kecil ini terlihat seperti retasan? Kami bekerja dengan beberapa angka kecil di atas baik-baik saja — tetapi sebenarnya tidak terlalu kecil.

Jika saya membiarkan diri saya untuk terus berjalan, Anda akan pergi melihat panjangnya artikel ini dan tidak akan sampai sejauh ini. Mungkin kami akan menjawab pertanyaan itu di lain hari .