Statistik Bayesian: Primer A/B Tester yang Cepat dan Bebas Hype
Diterbitkan: 2022-06-23
Seberapa yakin Anda dengan kemampuan Anda untuk menginterpretasikan hasil yang diberikan oleh alat pengujian A/B Anda?
Katakanlah, Anda menggunakan alat yang dibangun di atas statistik Bayesian, dan itu memberi tahu Anda bahwa "B" memiliki peluang 70% untuk mengalahkan "A" jadi "B" adalah pemenangnya. Apakah Anda tahu apa artinya dan bagaimana hal itu seharusnya menginformasikan strategi CRO Anda?
Dalam artikel ini, Anda akan mempelajari dasar-dasar statistik Bayesian yang akan membantu Anda kembali mengontrol pengujian A/B Anda, termasuk
- Tampilan statistik Bayesian yang tidak bias
- Keuntungan dan kerugian Frequentist vs Bayesian
- Persiapan yang Anda butuhkan untuk menafsirkan dan menggunakan hasil pengujian Bayesian A/B dengan percaya diri sambil menghindari beberapa jebakan mitos umum.
- Apa itu Statistik Bayesian?
- Kisah Asal Bayesian
- Contoh Statistik Bayesian yang Diterapkan pada Pengujian A/B
- Glosarium Singkat Istilah Bayesian yang Penting bagi Penguji A/B
- Inferensi Bayesian
- Probabilitas Bersyarat
- Distribusi Probabilitas/Distribusi Kemungkinan
- Distribusi Keyakinan Sebelumnya
- konjugasi
- Konjugasi Prior
- Fungsi Rugi
- Apa itu Statistik Sering?
- Pengujian A/B Bayesian vs Sering
- Kerangka Kerja Sering
- Kerangka Bayesian
- Apa yang Sebenarnya Diberitahukan Statistik Bayesian kepada Anda dalam Pengujian A/B?
- Peluang Menjadi Yang Terbaik (P2BB)
- Peningkatan yang Diharapkan
- Kerugian yang Diharapkan
- Mitos seputar Statistik Bayesian yang Harus Dihindari
- Mitos #1: Bayesian Menyatakan Asumsi Mereka, Orang yang Sering Tidak
- Mitos #2. Metode Bayesian Memberi Anda Jawaban yang Sebenarnya Anda Inginkan
- Mitos #3: Inferensi Bayesian Membantu Anda Mengkomunikasikan Ketidakpastian Lebih Baik Daripada Inferensi Sering
- Mitos #4. Hasil Pengujian A/B Bayesian Kebal terhadap Pengintipan
- Mitos #5. Statistik Frequentist Tidak Efisien Karena Anda Harus Menunggu Ukuran Sampel Tetap
- Jadi, Pilih Bayesian atau Frequentist? Ada Tempat untuk Keduanya.
- Takeaway kunci
Siap? Mari kita mulai dengan dasar-dasarnya.
Apa itu Statistik Bayesian?
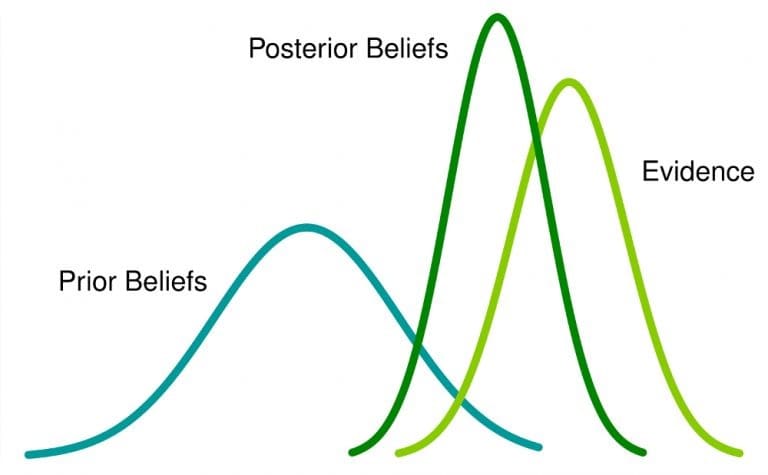
Statistik Bayesian adalah pendekatan analisis statistik yang didasarkan pada teorema Bayes, yang memperbarui keyakinan tentang peristiwa saat data atau bukti baru tentang peristiwa tersebut dikumpulkan. Di sini, probabilitas adalah ukuran keyakinan bahwa suatu peristiwa terjadi.
Apa artinya ini: Jika Anda memiliki keyakinan sebelumnya tentang suatu peristiwa, dan mendapatkan lebih banyak informasi terkait dengannya, keyakinan itu akan berubah (atau setidaknya disesuaikan) menjadi keyakinan posterior .
Ini berguna untuk memahami ketidakpastian atau saat bekerja dengan banyak data yang bising, seperti dalam pengoptimalan tingkat konversi untuk e-niaga dan dalam pembelajaran mesin.
Mari kita gambarkan ini:
Katakanlah, misalnya, Anda sedang menonton perlombaan kereta belanjaan perguruan tinggi dan kemudian seorang penonton yang bersemangat menantang Anda untuk bertaruh bahwa pria berkaos merah yang membawa wanita berbaju hijau akan menang. Anda memikirkannya dan melawan bahwa pria berjaket hitam dan gadis berkerudung hitam akan menang sebagai gantinya.

Penonton lain di atas dan membisikkan tip kepada Anda, "Pria berkaos merah memenangkan 3 balapan terakhir dari 4 balapan." Apa yang terjadi dengan taruhan Anda? Anda tidak terlalu yakin lagi, kan?
Misalkan Anda juga mengetahui bahwa terakhir kali pria berjaket hitam mengenakan kacamata keberuntungannya, dia menang. Dan saat dia tidak memakainya, pria berkaos merah menang.
Hari ini, Anda melihat pria berjaket hitam itu memakai kacamata itu. Keyakinan Anda berubah lagi. Anda sekarang lebih percaya pada taruhan Anda, benar? Dalam cerita ini, Anda telah memperbarui keyakinan Anda setiap kali Anda mendapatkan bukti data baru. Itulah pendekatan Bayesian.
Kisah Asal Bayesian
Ketika Pendeta Thomas Bayes pertama kali memikirkan teorinya, dia tidak berpikir itu layak untuk dipublikasikan. Jadi, itu tetap dalam catatannya selama lebih dari satu dekade. Saat keluarganya meminta Richard Price untuk membaca catatannya, Price menemukan catatan yang membentuk dasar Teorema Bayes.
Ini dimulai dengan eksperimen pemikiran untuk Bayes. Dia berpikir untuk duduk dengan punggung menghadap meja yang rata dan persegi sempurna dan meminta asistennya melempar bola ke meja.
Bola bisa mendarat di mana saja di atas meja, tetapi Bayes mengira dia bisa menebak di mana dengan memperbarui tebakannya dengan informasi baru. Ketika bola mendarat di atas meja, dia akan meminta asistennya memberi tahu dia apakah bola itu mendarat di kiri atau kanan, di depan atau di belakang tempat bola sebelumnya mendarat.
Dia mencatat itu dan mendengarkan saat lebih banyak bola mendarat di atas meja. Dengan informasi tambahan seperti ini, dia menemukan bahwa dia dapat meningkatkan akurasi tebakannya dengan setiap lemparan. Hal ini membawa gagasan untuk memperbarui pemahaman kita saat kita memperoleh lebih banyak bukti dari pengamatan.
Pendekatan Bayesian untuk analisis data diterapkan di berbagai bidang seperti sains dan teknik, dan bahkan mencakup olahraga dan hukum.
Dalam eksperimen terkontrol acak online, khususnya pengujian A/B, Anda dapat menggunakan pendekatan Bayesian dalam 4 langkah:
- Identifikasi distribusi Anda sebelumnya.
- Pilih model statistik yang mencerminkan keyakinan Anda.
- Jalankan eksperimen.
- Setelah observasi, perbarui keyakinan Anda dan hitung distribusi posterior.
Anda memperbarui keyakinan Anda menggunakan seperangkat aturan yang disebut algoritma Bayesian.
Contoh Statistik Bayesian yang Diterapkan pada Pengujian A/B
Mari kita ilustrasikan contoh pengujian A/B Bayesian.
Bayangkan kami menjalankan pengujian A/B sederhana pada tombol CTA toko Shopify. Untuk “A”, kami menggunakan “Tambahkan ke Keranjang” dan untuk “B”, kami menggunakan “Tambahkan ke Keranjang Anda”.
Inilah cara seorang frequentist akan mendekati tes.
Ada dua dunia alternatif: Satu di mana A dan B tidak berbeda, jadi pengujian tidak akan menunjukkan perbedaan dalam rasio konversi. Itu hipotesis nol. Dan di dunia lain, ada perbedaan, jadi satu tombol akan bekerja lebih baik daripada yang lain.
Para frequentist akan menganggap kita hidup di dunia 1 di mana tidak ada perbedaan dalam tombol CTA, yaitu, dengan asumsi hipotesis nol itu benar. Dan kemudian mereka akan mencoba membuktikan kesalahan itu ke tingkat kepastian yang telah ditentukan sebelumnya yang disebut tingkat signifikansi.
Tapi beginilah cara Bayesian akan mendekati tes yang sama:
Mereka mulai dengan keyakinan sebelumnya bahwa kedua tombol A dan B memiliki peluang yang sama untuk menghasilkan tingkat konversi antara 0 dan 100%. Jadi, ada kesetaraan tombol langsung dari gerbang — keduanya memiliki peluang 50% untuk menjadi yang berkinerja terbaik.
Kemudian tes dimulai dan data dikumpulkan. Dari mengamati informasi baru, penguji A/B Bayesian akan memperbarui pengetahuan mereka. Jadi, jika B menunjukkan janji, mereka dapat mencapai keyakinan posterior berdasarkan pengamatan yang mengatakan, “B memiliki peluang 61% untuk mengalahkan A”.
Ada perbedaan inti antara kedua metode.
Itulah mengapa penting bagi kami untuk menjaga pendekatan yang tidak bias terhadap pengujian A/B Bayesian.
Sebagian besar alat pengujian A/B Bayesian — mungkin untuk tujuan pemasaran — mengambil sikap anti-frekuensi yang ekstrem dan mendorong argumen bahwa Bayesian lebih baik dalam memberi tahu Anda varian mana yang lebih “menguntungkan”.
Tetapi apakah pendekatan statistik tunggal untuk pengujian A/B memiliki hak eksklusif atas wawasan?
Jika seseorang mendorong argumen Bayesian lebih jauh, mereka mungkin dihadapkan pada penelitian di mana responden mengatakan bahwa mereka ingin mengetahui tindakan apa yang terbaik atau bahwa mereka ingin memaksimalkan keuntungan atau sesuatu yang serupa. Ini menempatkan pertanyaan dengan tegas di wilayah teori keputusan - sesuatu yang tidak dapat langsung dikatakan oleh inferensi Bayesian maupun inferensi frequentist.
Georgi Georgiev, pembuat Analytics-toolkit.com dan penulis “Metode Statistik dalam Pengujian A/B Online”
Kami akan menyelami detail ini secara singkat di bagian depan. Untuk saat ini, mari kita buat sisa primer ini mudah dipahami.
Glosarium Singkat Istilah Bayesian yang Penting bagi Penguji A/B
Inferensi Bayesian
Inferensi Bayesian memperbarui probabilitas hipotesis dengan data baru. Itu dibangun di sekitar keyakinan dan probabilitas.
Inferensi Bayesian memanfaatkan probabilitas bersyarat untuk membantu kita memahami bagaimana data memengaruhi keyakinan kita. Katakanlah kita mulai dengan keyakinan sebelumnya bahwa langit berwarna merah. Setelah melihat beberapa data, kita akan segera menyadari bahwa kepercayaan sebelumnya ini salah. Jadi, kami melakukan pembaruan Bayesian untuk memperbaiki model kami yang salah tentang warna langit, yang berakhir dengan keyakinan posterior yang lebih akurat .
Michael Berk dalam Menuju Ilmu Data
Probabilitas Bersyarat
Probabilitas bersyarat adalah probabilitas suatu peristiwa mengingat bahwa peristiwa lain terjadi. Artinya, peluang A dalam kondisi B.
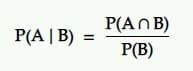
Terjemahan: Peluang terjadinya peristiwa A jika diberikan peristiwa B lainnya sama dengan peluang terjadinya B dan A bersama-sama dibagi dengan peluang terjadinya peristiwa B.
Distribusi Probabilitas/Distribusi Kemungkinan
Distribusi kemungkinan adalah distribusi yang menunjukkan seberapa besar kemungkinan data Anda akan mengasumsikan nilai tertentu.
Di mana data Anda dapat mengasumsikan beberapa nilai, misalnya, kategori seperti warna yang bisa menjadi abu-abu, merah, oranye, biru, dll., distribusi Anda multinomial. Untuk satu set angka, distribusi mungkin normal. Dan untuk nilai data yang bisa berupa ya/tidak atau benar/salah, itu akan menjadi binomial.
Distribusi Keyakinan Sebelumnya
Atau distribusi probabilitas sebelumnya, cukup disebut sebelumnya, mengungkapkan keyakinan Anda sebelum Anda mendapatkan bukti data baru. Jadi, ini adalah ekspresi dari keyakinan awal Anda yang akan Anda perbarui setelah mempertimbangkan beberapa bukti menggunakan analisis Bayesian (atau inferensi).
konjugasi
Pertama-tama, konjugasi mengacu pada bergabung bersama, biasanya berpasangan. Dalam teori probabilitas Bayesian, konjugasi mengasumsikan prior terkonjugasi dengan kemungkinan.
Jika posterior memiliki bentuk fungsional yang sama dengan prior, maka prior terkonjugasi dengan fungsi kemungkinan. Ini menunjukkan bagaimana fungsi kemungkinan memperbarui distribusi sebelumnya.
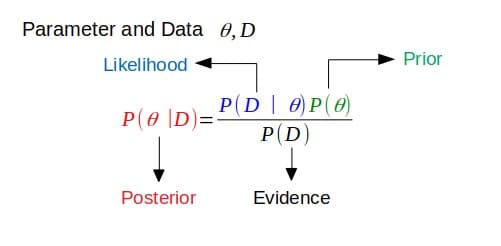
Konjugasi Prior
Hal ini terkait dengan definisi di atas. Jika posterior berada dalam keluarga distribusi probabilitas yang sama (atau memiliki bentuk fungsional yang sama) dengan distribusi probabilitas sebelumnya, maka prior dan posterior adalah distribusi konjugasi. Dalam hal ini, prior disebut konjugat sebelumnya untuk fungsi kemungkinan.
Mereka bisa subjektif (berdasarkan pengetahuan eksperimen), objektif dan informatif (berdasarkan data historis), atau non-informatif.
Fungsi Rugi
Fungsi kerugian adalah cara untuk mengukur kerugian dengan mengukur seberapa buruk perkiraan kita saat ini. Ini membantu kami meminimalkan kerugian untuk pengujian hipotesis, terutama saat mengungkapkan kesimpulan yang terletak pada kisaran nilai yang mungkin, dan mendukung pengambilan keputusan dengan hasil pengujian kami.
Sekarang sudah keluar dari jalan, kita bisa melanjutkan.
Jika Anda telah berada di sekitar blok untuk sementara waktu, Anda mungkin menemukan lebih dari beberapa meme statistik Frequentist vs Bayesian.

Kedua belah pihak tampaknya mencari jawaban dari arah yang berlawanan, tetapi benarkah demikian? Untuk memahami ini lebih baik (sambil tetap tidak memihak), mari kita kunjungi kamp Frequentists.
Apa itu Statistik Sering?
Ini adalah teknik inferensial pertama yang dipelajari kebanyakan orang dalam statistik. Statistik frequentist menghitung probabilitas bahwa suatu peristiwa (hipotesis) sering terjadi dalam kondisi yang sama.
Pengujian hipotesis A/B menggunakan pendekatan frequentist mengikuti langkah-langkah berikut:
- Nyatakan beberapa hipotesis. Biasanya, hipotesis nol adalah bahwa varian baru "B" tidak lebih baik dari "A" asli, sedangkan hipotesis alternatif menyatakan sebaliknya.
- Tentukan ukuran sampel terlebih dahulu menggunakan penghitungan daya statistik , kecuali jika Anda menggunakan pendekatan pengujian berurutan. Gunakan kalkulator ukuran sampel yang mempertimbangkan kekuatan statistik, tingkat konversi saat ini, dan efek minimum yang dapat dideteksi.
- Jalankan pengujian dan tunggu hingga setiap variasi terpapar pada ukuran sampel yang telah ditentukan sebelumnya.
- Hitung probabilitas mengamati hasil setidaknya sama ekstremnya dengan data di bawah hipotesis nol (nilai-p). Tolak hipotesis nol dan terapkan varian baru ke produksi jika nilai p < 5%.
Bagaimana ini dibandingkan dengan Bayesian? Ayo lihat…
Pengujian A/B Bayesian vs Sering
Ini adalah perdebatan terkenal di mana pun inferensi statistik digunakan. Dan terus terang, itu tidak ada gunanya. Keduanya memiliki kelebihan dan contoh di mana mereka adalah metode terbaik untuk digunakan.
Bertentangan dengan apa yang akan Anda pikirkan oleh sebagian besar promotor di kedua kubu, mereka serupa dalam beberapa hal dan tidak ada yang lebih mendekati kebenaran daripada yang lain — meskipun pendekatan mereka berbeda.
Ketika diterapkan pada pengujian A/B, misalnya, tidak ada metode khusus yang akan memberi Anda prediksi absolut dan akurat dalam hal tindakan yang akan menyebabkan pertumbuhan bisnis. Sebaliknya, pengujian A/B membantu Anda menghilangkan risiko dari pengambilan keputusan.
Tidak peduli bagaimana Anda menganalisis data Anda – menggunakan pendekatan Bayesian atau Frequentist – Anda dapat bergerak dengan beberapa tingkat kepastian bahwa Anda benar.
Dan untuk alasan itu, kedua model statistik tersebut valid. Bayesian mungkin memiliki keunggulan kecepatan tetapi lebih menuntut komputasi daripada Frequentist.
Lihat perbedaan lainnya…
Kerangka Kerja Sering
Sebagian besar dari kita akrab dengan pendekatan frequentist dari kursus statistik pengantar. Kami mendefinisikan metodologi di atas — mulai dari menyatakan hipotesis nol, menentukan ukuran sampel, mengumpulkan data melalui eksperimen acak, dan akhirnya mengamati hasil yang signifikan secara statistik.
Dalam Frequentism, kami melihat probabilitas secara mendasar terkait dengan frekuensi kejadian berulang. Jadi, dalam lemparan koin yang adil, seorang Frequentist percaya bahwa jika mereka cukup sering menebak, mereka akan mendapatkan kepala yang benar 50% dari waktu dan hal yang sama untuk ekor.
Pola pikir frequentist: “Jika saya mengulangi eksperimen dalam kondisi yang sama berulang-ulang, seberapa besar peluang metode saya mendapatkan jawaban yang benar?”
Kerangka Bayesian
Sementara pendekatan frequentist memperlakukan parameter populasi untuk setiap varian sebagai konstanta (tidak diketahui), pendekatan Bayesian memodelkan setiap nilai parameter sebagai variabel acak dengan beberapa distribusi probabilitas.
Di sini, Anda menghitung distribusi probabilitas (dan dengan demikian nilai yang diharapkan) untuk parameter yang diinginkan secara langsung.
Dan untuk memodelkan distribusi probabilitas untuk setiap varian, kami mengandalkan aturan Bayes untuk menggabungkan hasil eksperimen dengan pengetahuan sebelumnya yang kami miliki tentang metrik yang diminati. Kita dapat menyederhanakan perhitungan dengan menggunakan konjugat sebelumnya.
Alex Birkett merangkum algoritma Bayesian dengan cara ini:
- Tentukan distribusi sebelumnya yang menggabungkan keyakinan subjektif Anda tentang suatu parameter. Prior bisa tidak informatif atau informatif.
- Mengumpulkan data.
- Perbarui distribusi Anda sebelumnya dengan data menggunakan teorema Bayes (meskipun Anda dapat memiliki metode Bayesian tanpa menggunakan aturan Bayes secara eksplisit—lihat Bayesian non-parametrik) untuk mendapatkan distribusi posterior. Distribusi posterior adalah distribusi probabilitas yang mewakili keyakinan Anda yang diperbarui tentang parameter setelah melihat data.
- Analisis distribusi posterior dan rangkum (rata-rata, median, sd, kuantil…).
Singkatnya, eksperimen Bayesian berfokus pada perspektif mereka sendiri dan apa arti probabilitas bagi mereka. Pendapat mereka berkembang dengan data yang diamati. Sering kali, di sisi lain, percaya bahwa jawaban yang benar ada di suatu tempat.

Pahami bahwa debat Frequentist vs Bayesian tidak terlalu memengaruhi analisis pengujian A/B pasca. Perbedaan utama antara kedua kubu lebih terkait dengan apa yang bisa diuji.
Statistik probabilitas umumnya tidak banyak digunakan dalam analisis selanjutnya. Argumen Bayesian-Frequentist lebih dapat diterapkan mengenai pilihan variabel yang akan diuji dalam paradigma A/B, tetapi bahkan di sana sebagian besar penguji A/B melanggar hipotesis penelitian, probabilitas, dan interval kepercayaan .
Rob Balon ke CXL
Georgi lebih lanjut menguraikan:
Ada beberapa kalkulator Bayesian online dan setidaknya satu vendor perangkat lunak pengujian A/B utama yang menerapkan mesin statistik Bayesian yang semuanya menggunakan apa yang disebut prior non-informatif (sedikit keliru, tapi jangan gali ini). Dalam kebanyakan kasus, hasil dari alat ini bertepatan secara numerik dengan hasil dari tes frequentist pada data yang sama. Katakanlah alat Bayesian akan melaporkan sesuatu seperti '96% probabilitas bahwa B lebih baik daripada A' sedangkan alat frequentist akan menghasilkan nilai-p 0,04 yang sesuai dengan tingkat kepercayaan 96%.
Dalam situasi seperti di atas, yang jauh lebih umum daripada yang ingin diakui beberapa orang, kedua metode akan mengarah pada inferensi yang sama dan tingkat ketidakpastian akan sama, bahkan jika interpretasinya berbeda.
Apa yang akan dikatakan seorang Bayesian tentang hasil ini? Apakah itu mengubah nilai-p menjadi probabilitas posterior yang tepat saat melihat skenario di mana tidak ada informasi sebelumnya? Atau apakah semua aplikasi tes Bayesian ini salah arah karena menggunakan prior non-informatif itu sendiri?
Sebenarnya tidak perlu memilih kamp dan menemukan tempat di balik perlindungan untuk melempar batu ke kamp lain. Bahkan ada bukti bahwa kedua kerangka kerja menghasilkan hasil yang sama. Tidak peduli jalan yang Anda pilih, tujuannya mungkin akan sama. Itu tergantung pada bagaimana Anda bisa sampai di sana dengan Frequentist vs Bayesian.
Contohnya:
- Ada data yang menunjukkan pengujian Bayesian lebih cepat dan pilihan yang lebih disukai untuk eksperimen interaktif:
Karena paradigma Bayesian memungkinkan peneliti untuk secara formal mengukur keyakinan dan memasukkan pengetahuan tambahan, ini lebih cepat daripada analisis statistik tradisional.
Dalam simulasi pengujian A/B Bayesian, ketika kriteria keputusan disesuaikan (yaitu meningkatkan toleransi terhadap kesalahan), 75% eksperimen berakhir dalam 22,7% pengamatan yang diperlukan oleh pendekatan tradisional (pada tingkat signifikansi 5%). Dan itu hanya mencatat kesalahan tipe II 10%. - Bayesian juga dianggap lebih pemaaf, sedangkan Frequentist menghindari risiko:
Sementara banyak tes Frequentist menggunakan signifikansi statistik 95%, Bayesian dapat puas dengan kurang dari itu. Jika sebuah varian memiliki peluang 78% untuk mengalahkan kontrol, tergantung pada kerugian yang diharapkan, itu bisa menjadi keputusan yang baik untuk menerapkan varian itu.
Jika Anda salah dan kerugian yang diharapkan kurang dari satu persen, itu adalah kerusakan yang cukup kecil bagi banyak bisnis. Pendekatan suka berkelahi ini mungkin lebih cocok untuk pengambilan keputusan cepat dalam skenario berisiko sangat rendah. - Namun, simulasi dan perhitungan Bayesian adalah komputasi yang berat:
Frequentist, di sisi lain, berbasis pena dan kertas. Peringatan: Jika alat pengujian A/B Anda menggunakan Bayesian dan Anda tidak tahu asumsi apa yang ditambahkan ke data Anda, maka Anda tidak dapat mengandalkan "jawaban" yang diberikan vendor Anda. Ambil dengan sejumput garam. Dan jalankan analisis Anda sendiri.
Tidak semua sinar matahari dan pelangi dengan Bayesian. Seperti yang ditunjukkan Georgi dengan daftar pertanyaan ini:
- "Apakah Anda ingin mendapatkan produk dari probabilitas sebelumnya dan fungsi kemungkinan?"
- "Apakah Anda ingin campuran probabilitas dan data sebelumnya sebagai output?"
- "Apakah Anda ingin keyakinan subjektif dicampur dengan data untuk menghasilkan output?" (jika menggunakan prior informatif)
- "Apakah Anda merasa nyaman menyajikan statistik di mana ada informasi sebelumnya yang dianggap sangat pasti bercampur dengan data aktual?"
Ini semua adalah aspek statistik Bayesian, dalam istilah awam.
Apa yang Sebenarnya Diberitahukan Statistik Bayesian kepada Anda dalam Pengujian A/B?
Anda merancang pengujian A/B untuk memberikan wawasan tentang bagaimana perubahan memengaruhi metrik minat Anda, seperti tingkat konversi atau pendapatan per pengunjung.
Saat Anda menggunakan alat yang bekerja dengan statistik Bayesian, penting untuk memahami apa arti hasil Anda karena "B adalah pemenangnya" tidak berarti persis seperti yang dipikirkan kebanyakan orang.
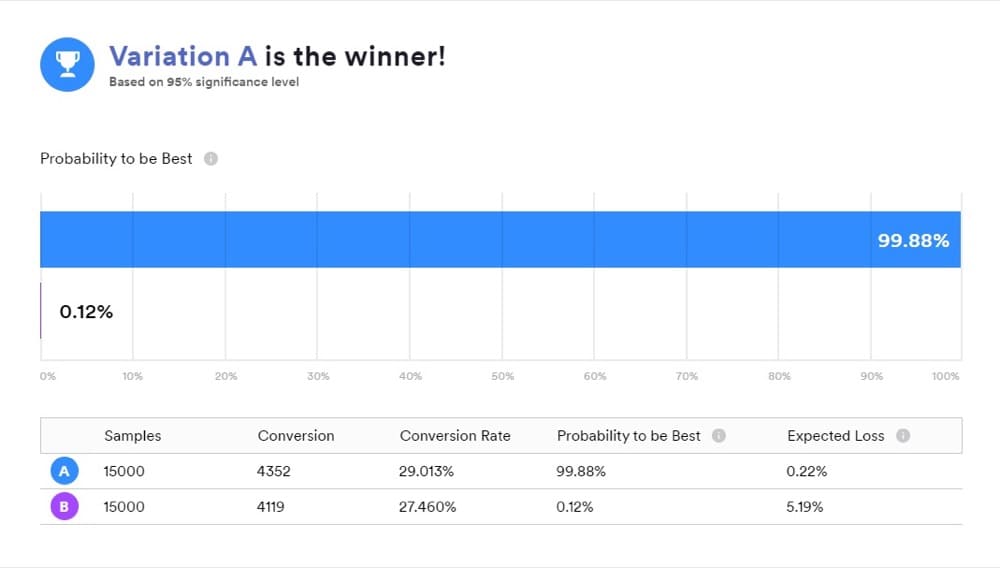
Ini adalah cara yang nyaman untuk menyajikan hasil, tetapi bukan itu yang diungkapkan oleh tes Anda. Sebaliknya, jawaban yang Anda inginkan berada dalam perbandingan posterior "A" dan "B".
Berikut adalah 3 metode perbandingan:
Peluang Menjadi Yang Terbaik (P2BB)
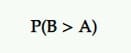
Ini adalah probabilitas yang menyatakan pemenang dalam pengujian A/B Bayesian.
Varian dengan probabilitas menjadi yang terbaik adalah varian dengan probabilitas tertinggi untuk terus mengungguli yang lain.
Ini dihitung dari satu set sampel posterior ukuran minat dari yang asli dan penantang.
Jadi, jika B memiliki probabilitas tertinggi untuk meningkatkan tingkat konversi Anda, misalnya, B dinyatakan sebagai pemenang.
Peningkatan yang Diharapkan
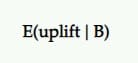
Jadi, jika B adalah pemenangnya, berapa banyak peningkatan yang harus kita harapkan darinya? Apakah itu akan terus memberikan hasil yang sama seperti yang kita lihat dalam pengujian?
Itulah wawasan yang diharapkan dapat diberikan oleh peningkatan. Peningkatan yang diharapkan dari memilih B daripada A, mengingat satu set sampel posterior, didefinisikan sebagai interval kredibel (atau rata-rata) dari peningkatan persentase.
Dalam pengujian A/B, kami biasanya membandingkan ini sebagai penantang dengan kontrol. Jadi, jika penantang kalah, itu diwakili dalam nilai negatif (seperti -11,35%) dan nilai positif (seperti +9,58%) jika menang.
Kerugian yang Diharapkan
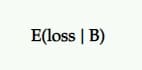
Karena tidak ada probabilitas 100% bahwa B lebih baik dari A, maka ada kemungkinan mencatat kerugian jika Anda memilih B daripada A. Ini direpresentasikan sebagai kerugian yang diharapkan dan, seperti halnya dengan peningkatan yang diharapkan, dinyatakan dari sudut pandang penantang terhadap kontrol.
Ini memberi tahu Anda risiko memilih varian P2BB Anda (yaitu, pemenang yang dinyatakan).
Sebelum kita menyelami mitos, terima kasih sebesar-besarnya kepada legenda analitik Georgi Georgiev. Analisis mendalamnya tentang inferensi frequentist vs Bayesian serta probabilitas dan statistik Bayesian dalam pengujian A/B menginspirasi bagian berikutnya.
Mitos seputar Statistik Bayesian yang Harus Dihindari
Dengan persaingan yang hampir setua itu, debat Bayesian vs Frequentist telah mengumpulkan banyak masukan — dan menimbulkan banyak mitos.
Mitos terbesar ini (mitos #2) dipromosikan oleh vendor alat pengujian A/B untuk memberi tahu Anda mengapa satu pendekatan lebih baik daripada yang lain.
Tapi setelah membaca bagian di atas, Anda lebih tahu.
Mari kita ungkap lubang-lubang dalam mitos-mitos ini.
Mitos #1: Bayesian Menyatakan Asumsi Mereka, Orang yang Sering Tidak
Ini menunjukkan bahwa Bayesian membuat asumsi dalam bentuk distribusi sebelumnya dan ini terbuka untuk penilaian. Tapi Frequentists membuat asumsi yang tersembunyi di tengah matematika.
Mengapa salah: Bayesian dan Frequentist membuat asumsi dasar yang serupa, satu-satunya perbedaan adalah Bayesian membuat asumsi tambahan — di atas matematika.
Model frequentist menggunakan asumsi dalam matematika, seperti bentuk distribusi, homogenitas atau heterogenitas efek di seluruh pengamatan, dan independensi pengamatan. Dan mereka tidak disembunyikan. Bahkan, mereka dibahas secara luas di komunitas statistik dan dinyatakan untuk setiap uji statistik frequentist.
Kebenaran: Frequentist secara eksplisit menyatakan asumsi mereka dan mengambil langkah lebih jauh untuk menguji asumsi: uji normalitas, uji kecocokan (di mana kami memiliki uji ketidakcocokan rasio sampel), dan banyak lagi.
Mitos #2. Metode Bayesian Memberi Anda Jawaban yang Sebenarnya Anda Inginkan
Kesalahpahaman di sini adalah bahwa nilai-p dan interval kepercayaan tidak memberi tahu penguji apa yang ingin mereka ketahui, sementara probabilitas posterior dan interval kredibel melakukannya. Orang ingin tahu hal-hal seperti
- Probabilitas bahwa B mengungguli A dan
- Kemungkinan bahwa hasilnya bukanlah suatu kebetulan.
Nilai-P dan uji hipotesis (inferensi lurus) tidak memberikan info itu, tetapi inferensi terbalik.
Mengapa salah: Ini adalah pertanyaan linguistik. Umumnya, ketika ahli non-statistik menggunakan istilah seperti "kemungkinan", "kesempatan", dan "probabilitas", mereka tidak menggunakannya dengan mempertimbangkan makna teknisnya. Selidiki lebih dalam dan Anda akan menemukan bahwa mereka sama bingungnya dengan inferensi terbalik seperti halnya tentang inferensi lurus.
Menurut Georgi Georgiev, pertanyaan seperti ini mulai muncul:
- “ Berapa probabilitas sebelumnya? Nilai apa yang dibawanya?”
- “Apa itu fungsi kemungkinan?”
- "Probabilitas 'sebelumnya' apa, saya tidak punya data sebelumnya?"
- "Bagaimana saya mempertahankan pilihan probabilitas sebelumnya?"
- "Apakah ada cara untuk mengomunikasikan apa yang dikatakan data, tanpa campuran ini?"
Kebenaran: Harus ada wawasan yang lebih baik tentang apa yang ingin diketahui penguji, bukan salah tafsir istilah teknis. Nilai-P, interval kepercayaan, dan lainnya memberi tahu Anda seberapa baik hasil yang diperiksa dengan data yang dikumpulkan. Mereka memberikan ukuran kepastian tanpa pengaruh subjektif, asumsi sebelumnya yang tidak diuji.
Mitos #3: Inferensi Bayesian Membantu Anda Mengkomunikasikan Ketidakpastian Lebih Baik Daripada Inferensi Sering
Karena hasil tes menghasilkan wawasan yang lebih “bermakna”.
Mengapa ini salah: Pendekatan Frequentist dan Bayesian memiliki alat serupa untuk membantu Anda mengomunikasikan kepastian dan hasil pengujian A/B Anda.
| Sering | Bayesian | ||||||||||
| ● Perkiraan poin | ● Perkiraan poin | ||||||||||
| ● Nilai-P | ● Interval yang kredibel | ||||||||||
| ● Interval keyakinan | ● Faktor Bayes | ||||||||||
| ● Kurva nilai-P | ● Distribusi posterior (menyelesaikan tugas yang sama sebagai kurva Frequentist) | ||||||||||
| ● Kurva kepercayaan diri | |||||||||||
| ● Kurva keparahan, dll. |
Kebenaran: Itu semua tergantung pada bagaimana Anda menggunakannya. Kedua metode tersebut sama-sama efektif dalam mengkomunikasikan ketidakpastian. Namun, ada perbedaan dalam cara mereka menyajikan ukuran ketidakpastian.
Mitos #4. Hasil Pengujian A/B Bayesian Kebal terhadap Pengintipan
Beberapa ahli statistik Bayesian berpendapat Anda dapat menghentikan tes Bayesian setelah Anda melihat "pemenang yang jelas" dan itu membuat sedikit perbedaan pada hasil akhirnya.
Anda mungkin tahu bahwa ini tidak dapat diterima dalam pengujian Frequentist, jadi ini dianggap sebagai kerugian jika dibandingkan dengan Bayesian. Tapi apakah itu benar-benar?
Mengapa ini salah: Dalam sebuah studi tahun 1969 di Journal of the Royal Statistical Society berjudul “Repeated Significance Tests on Accumulating Data”, Armitage et al. menunjukkan bagaimana penghentian opsional berbasis hasil meningkatkan kemungkinan kesalahan.
Anda tidak bisa berhenti begitu saja ketika Anda melihat pemenang, memperbarui posterior Anda, dan menggunakannya sebagai prior berikutnya tanpa menyesuaikan cara kerja analisis Bayesian.
Kebenarannya: Mengintip memengaruhi inferensi Bayesian seperti halnya Frequentist (jika Anda ingin melakukannya dengan benar).
Mitos #5. Statistik Frequentist Tidak Efisien Karena Anda Harus Menunggu Ukuran Sampel Tetap
Beberapa anggota komunitas CRO percaya bahwa uji statistik frequentist harus dijalankan dengan ukuran sampel yang telah ditentukan sebelumnya, jika tidak, hasilnya tidak valid.
Akibatnya, Anda menunggu lebih lama dari yang diperlukan untuk mendapatkan hasil yang Anda inginkan.
Mengapa salah: Statistik frequentist tidak digunakan seperti itu selama sekitar tujuh dekade sekarang. Dengan pengujian sekuensial yang sering dilakukan, Anda tidak memerlukan durasi tetap yang telah ditentukan sebelumnya.
Kebenarannya: Tes berurutan, yang lebih populer saat ini, memerlukan ukuran sampel maksimum untuk mengimbangi kesalahan tipe I dan tipe II, tetapi ukuran sampel aktual yang digunakan bervariasi dari kasus ke kasus tergantung pada hasil yang diamati.
Jadi, Pilih Bayesian atau Frequentist? Ada Tempat untuk Keduanya.
Tidak perlu memilih sisi. Kedua metode memiliki tempat mereka. Misalnya, proyek jangka panjang yang menggunakan prioritas yang diperbarui dan membutuhkan hasil cepat yang lebih baik dengan pendekatan Bayesian.
Metode Frequentist, di sisi lain, paling cocok untuk proyek-proyek yang membutuhkan jumlah pengulangan yang signifikan dalam hasilnya. Seperti dalam menulis perangkat lunak yang akan digunakan banyak orang dengan banyak kumpulan data.
Seperti yang dikatakan Cassie Kozyrkov, Head of Decision Intelligence di Google, “Statistik adalah ilmu untuk mengubah pikiran Anda di bawah ketidakpastian”.
Dalam video ringkasan Bayesian vs Frequentist Statistics-nya, dia berkata:
“Anda dapat mengambil debat Frequentist dan Bayesian dan meruntuhkan semuanya menjadi apa yang Anda ubah pikiran. Orang yang sering berubah pikiran tentang tindakan, mereka memiliki tindakan default yang lebih disukai — mungkin mereka tidak memiliki keyakinan apa pun — tetapi mereka memiliki tindakan yang mereka sukai di bawah ketidaktahuan dan kemudian mereka bertanya, “Apakah bukti [atau data] saya mengubah pikiran saya tentang tindakan itu?” "Apakah saya merasa konyol melakukannya berdasarkan bukti saya?"
Bayesians di sisi lain, berubah pikiran dengan cara yang berbeda. Mereka mulai dengan sebuah opini, opini pribadi yang diungkapkan secara matematis, yang disebut prior, dan kemudian mereka bertanya, "Apa opini yang masuk akal yang harus saya miliki setelah saya memasukkan beberapa bukti?" Jadi, Frequentist berubah pikiran tentang tindakan, Bayesian mengubah pikiran mereka tentang keyakinan.
Dan tergantung pada bagaimana Anda ingin membingkai pengambilan keputusan Anda, Anda mungkin lebih suka pergi dengan satu kamp dibandingkan yang lain.
Pada akhirnya, kita semua menuju kesimpulan yang sama — perbedaannya adalah bagaimana kesimpulan itu disajikan kepada Anda.
Jika inferensi frequentist dan Bayesian adalah fungsi pemrograman, dengan input menjadi masalah statistik, maka keduanya akan berbeda dalam apa yang mereka kembalikan ke pengguna. Fungsi inferensi frequentist akan mengembalikan angka, mewakili perkiraan (biasanya ringkasan statistik seperti rata-rata sampel, dll.), sedangkan fungsi Bayesian akan mengembalikan probabilitas.
Kutipan dari buku “Pemrograman Probabilistik & Metode Bayesian untuk Peretas
Yang kurang tepat adalah klaim bahwa yang satu memberikan hasil yang lebih praktis daripada yang lain.
Takeaway kunci
Statistik Bayesian dalam pengujian A/B terdiri dari 4 langkah berbeda:
- Identifikasi distribusi Anda sebelumnya
- Pilih model statistik yang mencerminkan keyakinan Anda
- Jalankan eksperimen
- Gunakan hasilnya untuk memperbarui keyakinan Anda dan hitung distribusi posterior
Hasil Anda akan mengarahkan Anda ke probabilitas yang berwawasan luas. Jadi, Anda akan tahu varian mana yang memiliki probabilitas tertinggi untuk menjadi yang terbaik, kerugian yang Anda harapkan, dan peningkatan yang Anda harapkan.
Ini biasanya ditafsirkan untuk Anda oleh sebagian besar alat pengujian A/B menggunakan statistik Bayesian. Tetapi seorang peneliti yang teliti akan melakukan analisis post-test untuk memahami hasil tersebut dengan lebih baik.
Karena Anda telah sampai sejauh ini, inilah fakta menyenangkan untuk Anda: Anda tahu potret Thomas Bayes yang semua orang kenal? Yang ini:

Tidak ada yang 100% yakin itu dia.