Erreurs de type I et de type II : les erreurs inévitables en optimisation

Les erreurs de type I et de type II se produisent lorsque vous repérez par erreur des gagnants dans vos expériences ou que vous ne les repérez pas. Avec les deux erreurs, vous finissez par choisir ce qui semble fonctionner ou non. Et pas avec les vrais résultats.

Une mauvaise interprétation des résultats des tests n'entraîne pas seulement des efforts d'optimisation malavisés, mais peut également faire dérailler votre programme d'optimisation à long terme.

Le meilleur moment pour détecter ces erreurs est avant même de les commettre ! Voyons donc comment vous pouvez éviter de rencontrer des erreurs de type I et de type II dans vos expériences d'optimisation.

Mais avant cela, regardons l'hypothèse nulle… car c'est le rejet ou le non-rejet erroné de l'hypothèse nulle qui provoque des erreurs de type I et de type II .

L'hypothèse nulle : ​H0

Lorsque vous faites l'hypothèse d'une expérience, vous ne sautez pas directement pour suggérer que la modification proposée déplacera une certaine métrique.

Vous commencez par dire que le changement proposé n'aura aucun impact sur la métrique concernée - qu'ils ne sont pas liés.

Ceci est votre hypothèse nulle (H0). H0 est toujours qu'il n'y a pas de changement. C'est ce que vous croyez, par défaut… jusqu'à (et si) votre expérience le réfute.

Et votre hypothèse alternative (Ha ou H1) est qu'il y a un changement positif. H0 et Ha sont toujours mathématiques opposés. Ha est celui où vous vous attendez à ce que le changement proposé fasse une différence, c'est votre hypothèse alternative - et c'est ce que vous testez avec votre expérience.

Ainsi, par exemple, si vous souhaitez exécuter un test sur votre page de tarification et y ajouter un autre mode de paiement, vous devez d'abord formuler une hypothèse nulle indiquant : le mode de paiement supplémentaire n'aura aucun impact sur les ventes. Votre hypothèse alternative se lirait : Le mode de paiement supplémentaire augmentera les ventes.

Mener une expérience, c'est en fait remettre en question l'hypothèse nulle ou le statu quo.

Les erreurs de type I et de type II se produisent lorsque vous rejetez ou ne rejetez pas par erreur l'hypothèse nulle.

Comprendre les erreurs de type I

Les erreurs de type I sont appelées faux positifs ou erreurs alpha.

Dans une instance d'erreur de type I de test d'hypothèse, votre test ou expérience d'optimisation * SEMBLE RÉUSSIR * et vous concluez (à tort) que la variation que vous testez se comporte différemment (meilleure ou pire) que l'originale.

Dans les erreurs de type I, vous voyez des remontées ou des baisses - qui ne sont que temporaires et ne se maintiendront probablement pas à long terme - et finissent par rejeter votre hypothèse nulle (et accepter votre hypothèse alternative).

Le rejet erroné de l'hypothèse nulle peut se produire pour diverses raisons, mais la principale est celle de la pratique de jeter un coup d'œil (c'est-à-dire, regarder vos résultats entre-temps ou lorsque l'expérience est toujours en cours). Et appeler les tests plus tôt que le critère d'arrêt défini n'est atteint.

De nombreuses méthodologies de test découragent la pratique de jeter un coup d'œil, car l'examen des résultats intermédiaires pourrait conduire à des conclusions erronées entraînant des erreurs de type I.

Voici comment vous pourriez faire une erreur de type I :

Supposons que vous optimisez la page de destination de votre site Web B2B et supposez que l'ajout de badges ou de récompenses réduira l'anxiété de vos prospects, augmentant ainsi le taux de remplissage de votre formulaire (entraînant plus de prospects).

Votre hypothèse nulle pour cette expérience devient donc : l' ajout de badges n'a aucun impact sur le remplissage des formulaires.

Le critère d'arrêt d'une telle expérience est généralement une certaine période et/ou après que X conversions se produisent au niveau de signification statistique défini. Classiquement, les optimiseurs essaient d'atteindre la marque de confiance statistique de 95 %, car cela vous laisse 5 % de chances de commettre l'erreur de type I, considérée comme suffisamment faible pour la plupart des expériences d'optimisation. En général, plus cette métrique est élevée, plus les risques de commettre des erreurs de type I sont faibles.

Le niveau de confiance que vous visez détermine quelle sera votre probabilité d'obtenir une erreur de type I (α).

Donc, si vous visez un niveau de confiance de 95 %, votre valeur pour α devient 5 %. Ici, vous acceptez qu'il y a 5 % de chances que votre conclusion soit erronée.

En revanche, si vous optez pour un niveau de confiance de 99 % avec votre expérience, votre probabilité d'obtenir une erreur de type I tombe à 1 %.

Disons, pour cette expérience, que vous devenez trop impatient et qu'au lieu d'attendre la fin de votre expérience, vous regardez le tableau de bord de votre outil de test (coup d'œil !) juste un jour après. Et vous remarquez une augmentation "apparente" - que votre taux de remplissage de formulaire a augmenté de 29,2 % avec un niveau de confiance de 95 %.

Et BAM…

… vous arrêtez votre expérience.

… rejeter l'hypothèse nulle (que les badges n'ont eu aucun impact sur les ventes).

… accepter l'hypothèse alternative (que les badges dopent les ventes).

… et courez avec la version avec les badges de récompenses.

Mais lorsque vous mesurez vos prospects au cours du mois, vous trouvez que le nombre est presque comparable à ce que vous avez rapporté avec la version originale. Les badges n'avaient pas tellement d'importance après tout. Et que l'hypothèse nulle a probablement été rejetée en vain.

Ce qui s'est passé ici, c'est que vous avez terminé votre expérience trop tôt et que vous avez rejeté l'hypothèse nulle et que vous vous êtes retrouvé avec un faux gagnant - en faisant une erreur de type I.

Éviter les erreurs de type I dans vos expériences

Un moyen sûr de réduire vos chances de tomber sur une erreur de type I consiste à utiliser un niveau de confiance plus élevé. Un niveau de signification statistique de 5 % (se traduisant par un niveau de confiance statistique de 95 %) est acceptable. C'est un pari que la plupart des optimiseurs feraient en toute sécurité car, ici, vous échouerez dans la plage improbable de 5 %.

En plus de définir un niveau de confiance élevé, il est important d'exécuter vos tests suffisamment longtemps. Les calculateurs de durée de test peuvent vous indiquer pendant combien de temps vous devez exécuter votre test (après avoir pris en compte des éléments tels qu'une taille d'effet spécifiée, entre autres). Si vous laissez une expérience suivre le cours prévu, vous réduisez considérablement vos chances de rencontrer l'erreur de type 1 (étant donné que vous utilisez un niveau de confiance élevé). Attendre jusqu'à ce que vous obteniez des résultats statistiquement significatifs garantit qu'il n'y a qu'une faible chance (généralement 5 %) que vous ayez rejeté l'hypothèse nulle par erreur et commis une erreur de type I. En d'autres termes, utilisez une bonne taille d'échantillon, car c'est essentiel pour obtenir des résultats statistiquement significatifs.

Maintenant, tout était question d'erreurs de type I liées au niveau de confiance (ou de signification) de vos expériences. Mais il existe également un autre type d'erreur qui peut se glisser dans vos tests - les erreurs de type II.

Comprendre les erreurs de type II

Les erreurs de type II sont appelées faux négatifs ou erreurs bêta.

Contrairement à l'erreur de type I, dans le cas d'une erreur de type II, l'expérience *SEMBLE ÉCHOUER (OU NON CONCLUANTE)* et vous concluez (à tort) que la variation que vous testez ne fait rien de différent de la original.

Dans les erreurs de type II, vous ne voyez pas les vrais ascenseurs ou creux et finissez par échouer à rejeter l'hypothèse nulle et à rejeter l'hypothèse alternative.

Voici comment vous pourriez commettre l'erreur de type II :

Revenir au même site Web B2B d'en haut…

Supposons donc que cette fois, vous émettiez l'hypothèse que l'ajout d'une clause de non-responsabilité de conformité GDPR bien en évidence en haut de votre formulaire encouragera davantage de prospects à le remplir (ce qui entraînera plus de prospects).

Par conséquent, votre hypothèse nulle pour cette expérience devient : la clause de non-responsabilité relative à la conformité au RGPD n'a pas d'incidence sur le remplissage des formulaires.

Et l'hypothèse alternative pour la même chose est la suivante : la clause de non-responsabilité relative à la conformité au RGPD entraîne davantage de remplissages de formulaires.

La puissance statistique d'un test détermine dans quelle mesure il peut détecter les différences de performances entre vos versions d'origine et challenger, en cas d'écarts. Traditionnellement, les optimiseurs essaient d'atteindre la barre de puissance statistique de 80 %, car plus cette métrique est élevée, plus les risques de commettre des erreurs de type II sont faibles.

La puissance statistique prend une valeur comprise entre 0 et 1 (et est souvent exprimée en %) et contrôle la probabilité de votre erreur de type II (β) ; il est calculé comme suit : 1 – β

Plus la puissance statistique de votre test est élevée, plus la probabilité de rencontrer des erreurs de type II sera faible.

Donc, si une expérience a une puissance statistique de 10 %, elle peut être très sensible à une erreur de type II. Alors que si une expérience a une puissance statistique de 80%, elle sera beaucoup moins susceptible de faire une erreur de type II.

Encore une fois, vous exécutez votre test, mais cette fois-ci, vous ne remarquez aucune amélioration significative dans le remplissage de vos formulaires. Les deux versions rapportent des conversions presque similaires. Pour cette raison, vous arrêtez votre expérience et continuez avec la version originale sans l'avertissement de conformité GDPR.

Cependant, au fur et à mesure que vous approfondissez vos données sur les prospects de la période d'expérimentation, vous constatez que si le nombre de prospects des deux versions (l'original et le challenger) semblait identique, la version GDPR vous a permis d'obtenir une bonne augmentation significative du nombre. de prospects en provenance d'Europe. (Bien sûr, vous auriez pu utiliser le ciblage d'audience pour montrer l'expérience uniquement aux prospects européens, mais c'est une autre histoire.)

Ce qui s'est passé ici, c'est que vous avez terminé votre test trop tôt, sans vérifier si vous aviez atteint une puissance suffisante - en faisant une erreur de type II.

Éviter les erreurs de type II dans vos expériences

Pour éviter les erreurs de type II, exécutez des tests avec une puissance statistique élevée. Essayez de configurer vos expériences de manière à atteindre au moins la barre des 80 % de puissance statistique. Il s'agit d'un niveau de puissance statistique acceptable pour la plupart des expériences d'optimisation. Avec lui, vous pouvez vous assurer que dans 80% des cas, au moins, vous rejeterez correctement une fausse hypothèse nulle.

Pour ce faire, vous devez examiner les facteurs qui s'y ajoutent.

Le plus important d'entre eux est la taille de l'échantillon (étant donné une taille d'effet observée). La taille de l'échantillon est directement liée à la puissance d'un test. Une taille d'échantillon énorme signifie un test de puissance élevée. Les tests sous-alimentés sont très vulnérables aux erreurs de type II car vos chances de détecter des différences dans les résultats de votre challenger et des versions originales diminuent considérablement, en particulier pour les faibles MEI (plus à ce sujet ci-dessous). Donc, pour éviter les erreurs de type II, attendez que le test accumule suffisamment de puissance pour minimiser les erreurs de type II. Idéalement, dans la plupart des cas, vous voudriez atteindre une puissance d'au moins 80 %.

Un autre facteur est l' effet d'intérêt minimum (MEI) que vous ciblez pour votre expérience. MEI (également appelé MDE) est la magnitude minimale de la différence que vous voudriez détecter dans votre KPI en question. Si vous définissez un MEI faible (en envisageant une augmentation de 1,5 %, par exemple), vos chances de rencontrer l'erreur de type II augmentent car la détection de petites différences nécessite des tailles d'échantillon sensiblement plus grandes (pour atteindre une puissance suffisante).

Enfin, il est important de noter qu'il existe généralement une relation inverse entre la probabilité de commettre une erreur de type I (α) et la probabilité de commettre une erreur de type II (β). Par exemple, si vous diminuez la valeur de α pour diminuer la probabilité de faire une erreur de type I (disons que vous fixez α à 1 %, ce qui signifie un niveau de confiance de 99 %), la puissance statistique de votre expérience (ou sa capacité, β , de détecter une différence lorsqu'elle existe) finit par diminuer également, augmentant ainsi votre probabilité d'obtenir une erreur de type II.

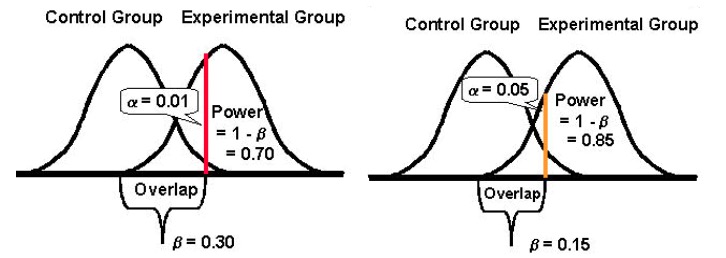
Accepter davantage l'une ou l'autre des erreurs : Type I et II (et trouver un équilibre)

La diminution de la probabilité d'un type d'erreur augmente celle de l'autre type (étant donné que tout le reste reste le même).

Et vous devez donc prendre l'appel sur le type d'erreur envers lequel vous pourriez être plus tolérant.

Faire une erreur de type I, d'une part, et déployer un changement pour tous vos utilisateurs pourrait vous coûter des conversions et des revenus - pire, pourrait également être un tueur de conversion.

Faire une erreur de type II, en revanche, et ne pas déployer une version gagnante pour tous vos utilisateurs pourrait, encore une fois, vous coûter les conversions que vous auriez pu gagner autrement.

Invariablement, les deux erreurs ont un coût.

Cependant, selon votre expérience, l'un pourrait être plus acceptable pour vous que l'autre. En général, les testeurs trouvent l' erreur de type I environ quatre fois plus grave que l'erreur de type II .

Si vous souhaitez adopter une approche plus équilibrée, le statisticien Jacob Cohen suggère que vous devriez opter pour une puissance statistique de 80 % qui s'accompagne d' un « équilibre raisonnable entre le risque alpha et bêta ». " (80 % de puissance est également la norme pour la plupart des outils de test.)

Et en ce qui concerne la signification statistique, la norme est fixée à 95 %.

Fondamentalement, tout est question de compromis et du niveau de risque que vous êtes prêt à tolérer. Si vous vouliez vraiment minimiser les risques d'erreurs, vous pourriez opter pour un niveau de confiance de 99 % et une puissance de 99 %. Mais cela signifierait que vous travailleriez avec des tailles d'échantillons incroyablement énormes pendant des périodes semblant éternellement longues. De plus, même dans ce cas, vous laisseriez une marge d'erreur.

De temps à autre, vous conclurez une expérience de manière erronée. Mais cela fait partie du processus de test - il faut un certain temps pour maîtriser les statistiques de test A/B. Enquêter et retester ou suivre vos expériences réussies ou ratées est un moyen de réaffirmer vos conclusions ou de découvrir que vous avez fait une erreur.