Réseau de neurones à un seul neurone sur Python - avec intuition mathématique

Publié: 2021-06-21

Construisons un réseau simple — très très simple, mais un réseau complet — avec une seule couche. Une seule entrée - et un neurone (qui est également la sortie), un poids, un biais.

Exécutons d'abord le code, puis analysons partie par partie

Clonez le projet Github ou exécutez simplement le code suivant dans votre IDE préféré.

Si vous avez besoin d'aide pour configurer un IDE, j'ai décrit le processus ici.

Si tout se passe bien, vous obtiendrez cette sortie :

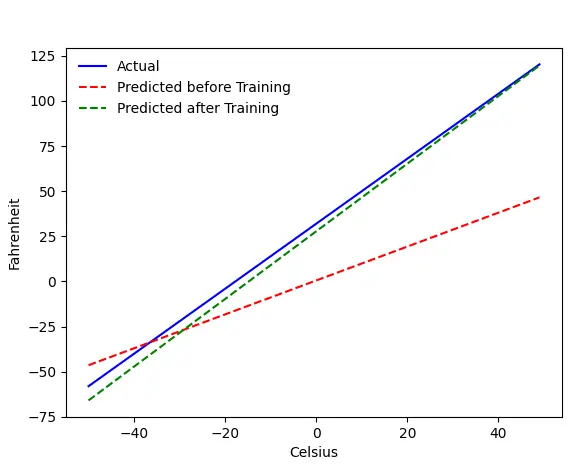
Le problème - Fahrenheit de Celsius

Nous entraînerons notre machine à prédire Fahrenheit à partir de Celsius. Comme vous pouvez le comprendre à partir du code (ou du graphique), la ligne bleue est la relation réelle Celsius-Fahrenheit. La ligne rouge est la relation prédite par notre baby machine sans aucune formation. Enfin, nous entraînons la machine, et la ligne verte est la prédiction après l'entraînement.

Regardez Line#65–67 - avant et après la formation, il prédit en utilisant la même fonction ( get_predicted_fahrenheit_values() ). Alors, que fait Magic Train() ? Découvrons-le.

Structure du réseau

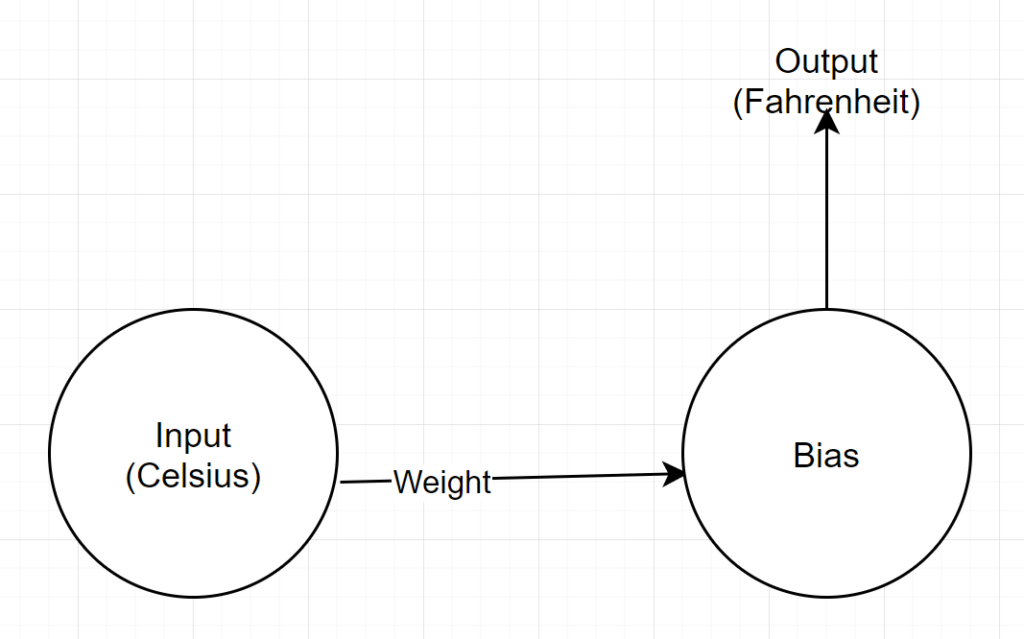
Entrée : un nombre représentant Celsius

Poids : Un flotteur représentant le poids

Biais : un flotteur représentant le biais

Sortie : un flotteur représentant les Fahrenheit prédits

Donc, nous avons au total 2 paramètres - 1 poids et 1 biais

Analyse de code

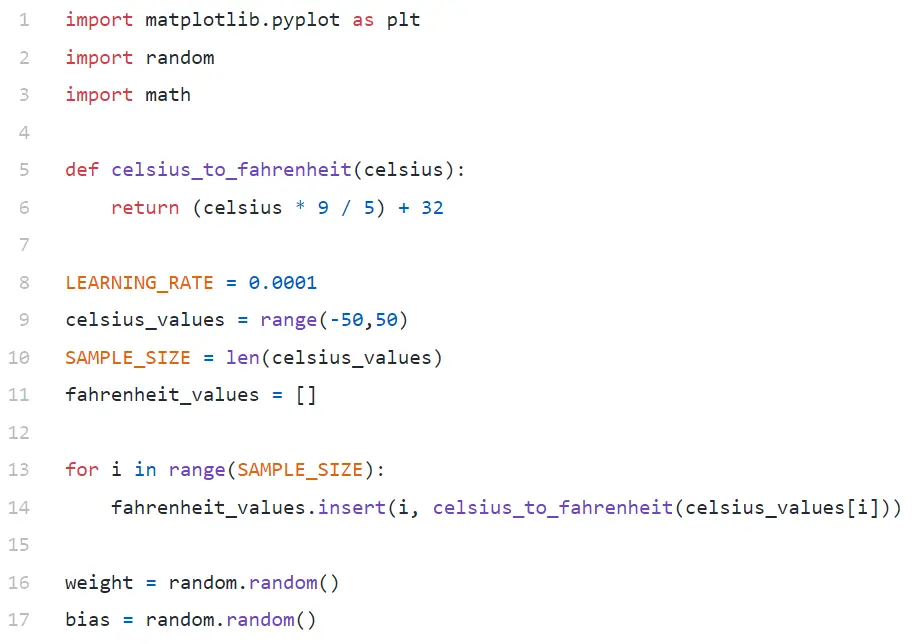
Dans Line#9, nous générons un tableau de 100 nombres entre -50 et +50 (à l'exclusion de 50 - la fonction de plage exclut la valeur limite supérieure).

Dans les lignes 11 à 14, nous générons le Fahrenheit pour chaque valeur Celsius.

Aux lignes 16 et 17, nous initialisons le poids et le biais.

train()

Nous exécutons 10000 itérations de formation ici. Chaque itération est composée de :

passe avant (Ligne#57)
passe arrière (Ligne#58)
update_parameters (Ligne #59)

Si vous débutez avec python, cela peut vous sembler un peu étrange — les fonctions python peuvent renvoyer plusieurs valeurs en tant que tuple .

Notez que update_parameters est la seule chose qui nous intéresse. Tout le reste que nous faisons ici est d'évaluer les paramètres de cette fonction, qui sont les gradients (nous expliquerons ci-dessous ce que sont les gradients) de notre poids et de notre biais.

grad_weight : un flotteur représentant le gradient de poids
grad_bias : un flotteur représentant le gradient de biais

Nous obtenons ces valeurs en appelant vers l'arrière, mais cela nécessite une sortie, que nous obtenons en appelant vers l'avant à la ligne 57.

avant()

Notez qu'ici celsius_values et fahrenheit_values sont des tableaux de 100 lignes :

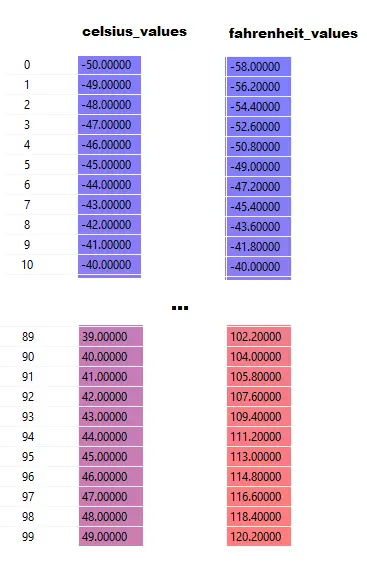
Après avoir exécuté la ligne # 20–23, pour une valeur Celsius, disons 42

sortie = 42 * poids + biais

Ainsi, pour 100 éléments dans celsius_values , la sortie sera un tableau de 100 éléments pour chaque valeur celsius correspondante.

Les lignes 25 à 30 calculent la perte à l'aide de la fonction de perte d'erreur quadratique moyenne (MSE), qui n'est qu'un nom fantaisiste du carré de toutes les différences divisé par le nombre d'échantillons (100 dans ce cas).

Une petite perte signifie une meilleure prédiction. Si vous continuez à imprimer la perte à chaque itération, vous verrez qu'elle diminue au fur et à mesure que l'apprentissage progresse.

Enfin, à la ligne 31, nous renvoyons la sortie et la perte prévues.

en arrière

Nous sommes seulement intéressés à mettre à jour notre pondération et notre biais. Pour mettre à jour ces valeurs, nous devons connaître leurs gradients, et c'est ce que nous calculons ici.

Notez que les gradients sont calculés dans l'ordre inverse. Le gradient de sortie est calculé en premier, puis pour le poids et le biais, et donc le nom "rétropropagation". La raison en est que pour calculer le gradient de poids et de biais, nous devons connaître le gradient de sortie - afin de pouvoir l'utiliser dans la formule de la règle de la chaîne .

Voyons maintenant ce que sont les règles de gradient et de chaîne.

Pente

Par souci de simplicité, considérons que nous n'avons qu'une seule valeur de celsius_values et fahrenheit_values , 42 et 107,6 respectivement.

Maintenant, la répartition du calcul à la ligne #30 devient :

perte = (107,6 - (42 * poids + biais))² / 1

Comme vous le voyez, la perte dépend de 2 paramètres - les poids et le biais. Considérez le poids. Imaginez, nous l'avons initialisé avec une valeur aléatoire, disons 0,8, et après avoir évalué l'équation ci-dessus, nous obtenons 123,45 comme valeur de loss . Sur la base de cette valeur de perte, vous devez décider comment vous allez mettre à jour le poids. Devriez-vous en faire 0,9 ou 0,7 ?

Vous devez mettre à jour le poids de manière à ce que lors de la prochaine itération, vous obteniez une valeur de perte inférieure (rappelez-vous que la réduction des pertes est l'objectif ultime). Donc, si l'augmentation du poids augmente la perte, nous la diminuerons. Et si l'augmentation du poids diminue la perte, nous l'augmenterons.

Maintenant, la question, comment savons-nous si l'augmentation du poids augmentera ou diminuera la perte. C'est là qu'intervient le dégradé . D'une manière générale, le gradient est défini par la dérivée. Rappelez-vous de votre calcul de lycée, ∂y/∂x (qui est la dérivée partielle/gradient de y par rapport à x) indique comment y changera avec un petit changement de x.

Si ∂y/∂x est positif, cela signifie qu'un petit incrément de x augmentera y.

Si ∂y/∂x est négatif, cela signifie qu'un petit incrément de x diminuera y.

Si ∂y/∂x est grand, un petit changement de x entraînera un grand changement de y.

Si ∂y/∂x est petit, un petit changement de x entraînera un petit changement de y.

Ainsi, à partir des gradients, nous obtenons 2 informations. Dans quelle direction le paramètre doit être mis à jour (augmentation ou diminution) et de combien (grand ou petit).

Règle de la chaîne

De manière informelle, la règle de la chaîne dit :

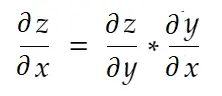
Prenons l'exemple de poids ci-dessus. Nous devons calculer grad_weight pour mettre à jour ce poids, qui sera calculé par :

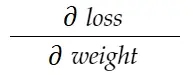
Avec la formule de la règle de la chaîne, nous pouvons la dériver :

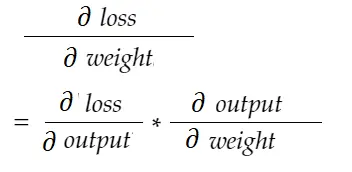
De même, gradient pour biais :

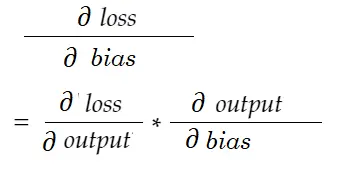
Dessinons un diagramme de dépendance.

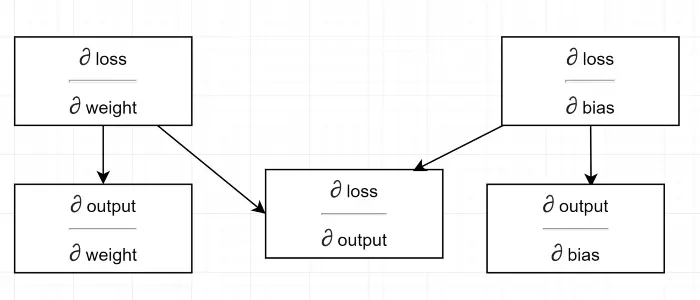
Voir tout le calcul dépend du gradient de sortie (∂ perte/∂ sortie) . C'est pourquoi nous le calculons d'abord sur le backpass (Ligne #34–36).

En fait, dans les frameworks ML de haut niveau, par exemple dans PyTorch, vous n'avez pas à écrire de codes pour le backpass ! Pendant la passe avant, il crée des graphiques de calcul, et pendant la passe arrière, il passe par la direction opposée dans le graphique et calcule les gradients à l'aide de la règle de la chaîne.

∂ perte / ∂ sortie

Nous définissons cette variable par grad_output dans le code, que nous avons calculé à la ligne #34–36. Découvrons la raison derrière la formule que nous avons utilisée dans le code.

N'oubliez pas que nous alimentons ensemble les 100 valeurs Celsius de la machine. Ainsi, grad_output sera un tableau de 100 éléments, chaque élément contenant le gradient de sortie pour l'élément correspondant dans celsius_values . Pour plus de simplicité, considérons qu'il n'y a que 2 éléments dans celsius_values .

Donc, en décomposant la ligne #30,

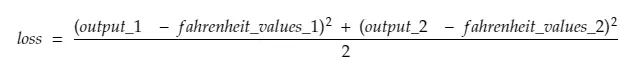
où,

output_1 = valeur de sortie pour la 1ère valeur Celsius

output_2 = valeur de sortie pour la 2ème valeur Celsius

fahreinheit_values_1 = Valeur Fahreinheit réelle pour la 1ère valeur Celsius

fahreinheit_values_1 = Valeur Fahreinheit réelle pour la 2ème valeur Celsius

Maintenant, la variable résultante grad_output contiendra 2 valeurs - gradient de output_1 et output_2, ce qui signifie :

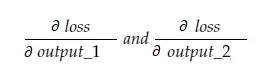
Calculons le gradient de output_1 uniquement, puis nous pouvons appliquer la même règle pour les autres.

L'heure du calcul !

Qui est identique à la ligne # 34–36.

Gradient de poids

Imaginez, nous n'avons qu'un seul élément dans celsius_values. À présent:

Ce qui est identique à la ligne # 38–40. Pour 100 celsius_values, les valeurs de gradient pour chacune des valeurs seront additionnées. Une question évidente serait de savoir pourquoi nous ne réduisons pas le résultat (c'est-à-dire en divisant par SAMPLE_SIZE). Puisque nous multiplions tous les gradients avec un petit facteur avant de mettre à jour les paramètres, ce n'est pas nécessaire (voir la dernière section Mise à jour des paramètres).

Dégradé de biais

Ce qui est identique à la ligne # 42. Comme les gradients de poids, ces valeurs pour chacune des 100 entrées sont additionnées. Encore une fois, c'est bien puisque les gradients sont multipliés par un petit facteur avant de mettre à jour les paramètres.

Mise à jour des paramètres

Enfin, nous mettons à jour les paramètres. Notez que les gradients sont multipliés par un petit facteur (LEARNING_RATE) avant d'être soustraits, pour rendre la formation stable. Une grande valeur de LEARNING_RATE entraînera un problème de dépassement et une valeur extrêmement faible ralentira la formation, ce qui pourrait nécessiter beaucoup plus d'itérations. Nous devrions trouver une valeur optimale pour cela avec quelques essais et erreurs. Il existe de nombreuses ressources en ligne, y compris celle-ci, pour en savoir plus sur l'apprentissage de Rate.

Notez que le montant exact que nous ajustons n'est pas extrêmement critique. Par exemple, si vous réglez un peu LEARNING_RATE , les variables descente_grad_weight et descente_grad_bias (Ligne #49–50) seront modifiées, mais la machine pourrait toujours fonctionner. L'important est de s'assurer que ces quantités sont dérivées en réduisant les gradients avec le même facteur (LEARNING_RATE dans ce cas). En d'autres termes, "maintenir la descente des gradients proportionnels" importe plus que "de combien ils descendent ".

Notez également que ces valeurs de gradient sont en fait la somme des gradients évalués pour chacune des 100 entrées. Mais comme ceux-ci sont mis à l'échelle avec la même valeur, c'est bien comme mentionné ci-dessus.

Afin de mettre à jour les paramètres, nous devons les déclarer avec le mot-clé global (à la ligne #47).

Où aller en partant d'ici

Le code serait beaucoup plus petit en remplaçant les boucles for par la compréhension de liste de manière pythonique. Jetez-y un coup d'œil maintenant - cela ne prendrait pas plus de quelques minutes pour comprendre.

Si vous avez tout compris jusqu'à présent, c'est probablement le bon moment pour voir les rouages d'un réseau simple avec plusieurs neurones/couches — voici un article.