Distribution normale - Une introduction intuitive sans mathématiques

J'essaierai de garder cet article exempt d'équations et de jargon bouché - autant que possible. Cependant, j'ai besoin que vous ayez au moins les capacités suivantes :

• Capable d'interpréter des graphiques simples.
• Connaissances de niveau élémentaire en probabilité. Vous comprenez au moins qu'il y a une probabilité de 50% pour la tête si je lance une pièce.
• Calcul intégral et physique quantique (je plaisante !)

Pourquoi la distribution normale

Une façon intuitive de comprendre quelque chose est de rechercher pourquoi c'est nécessaire. Faisons-le pour la distribution normale (également appelée distribution gaussienne).

Dites que vous avez une drôle d'habitude. Chaque jour, vous lancez une pièce 100 fois. Il est "normal" de s'attendre à avoir la tête 50 fois - ou près de 50 fois la majeure partie de la journée. Rarement, il y a de bons jours pour la tête - vous pouvez obtenir environ 55 fois et très rarement plus de 65 fois.

Maintenant, vous voulez quantifier cette "rareté". Donc, vous commencez à garder une trace du nombre de fois où vous avez eu la tête chaque jour.

Nombre de têtes chaque jour en un an

Vous trouverez ci-dessous les données après un an (365 jours) - la première est le nombre de têtes que vous avez obtenues le premier jour et la dernière est le nombre de têtes que vous avez obtenues le dernier jour. Vous n'avez pas besoin de vérifier tous les chiffres ci-dessous, mais il est facile de constater que la plupart d'entre eux se situent autour de 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Mieux visualiser avec l'histogramme

Traçons un histogramme à partir des données ci-dessus :

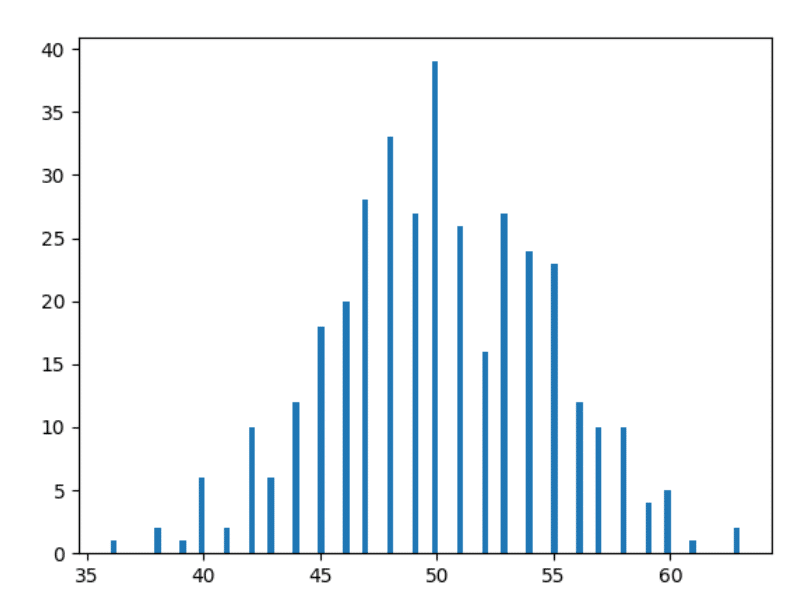
Ah ! Cela ne ressemble-t-il pas déjà à l'image que vous avez vue sur Internet lorsque vous avez recherché sur Google « Distribution normale » ? Nous y sommes presque!

Donc, si vous ne comprenez pas les histogrammes - nous venons de tracer ici le nombre de jours où nous avons obtenu un décompte particulier pour la tête. Par exemple, nous avons eu la tête 36 fois sur 2 jours particuliers de l'année (vérifiez les données ci-dessus si vous ne me croyez pas), c'est pourquoi il y a une barre de hauteur 2 unité sur le point horizontal à 36 (le rouge rectangle à gauche dans l'image ci-dessous).

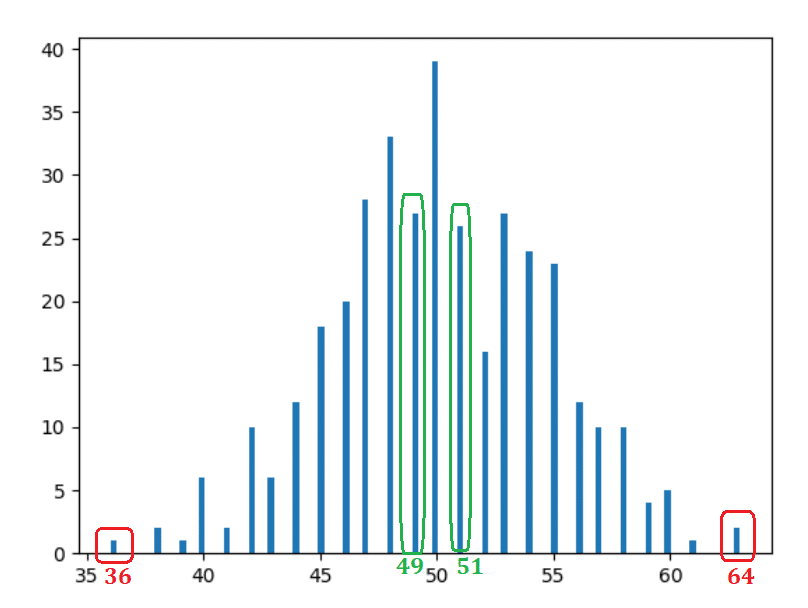
Observations

1. Assez évident et attendu - 50 têtes se sont produites la plupart du temps.
2. Plus on s'éloigne du centre (50), plus l'occurrence diminue.
3. Les barres à la même distance prennent des formes similaires. Par exemple, si vous déplacez une unité vers la gauche (49) ou la droite (51) — les occurrences sont similaires — 30 et 31 respectivement (les rectangles verts). Si vous vous déplacez de 14 unités vers la gauche (36) ou vers la droite (64), les occurrences sont à nouveau similaires — 2 et 1 respectivement (rectangles rouges).

Données sur 10 ans

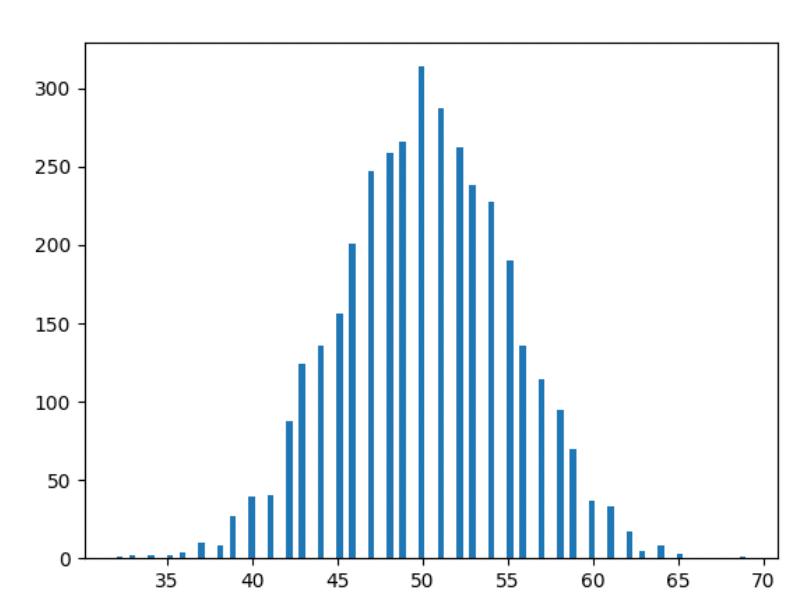
Maintenant, avançons un peu et traçons les données sur 10 ans.

1000 ans de données

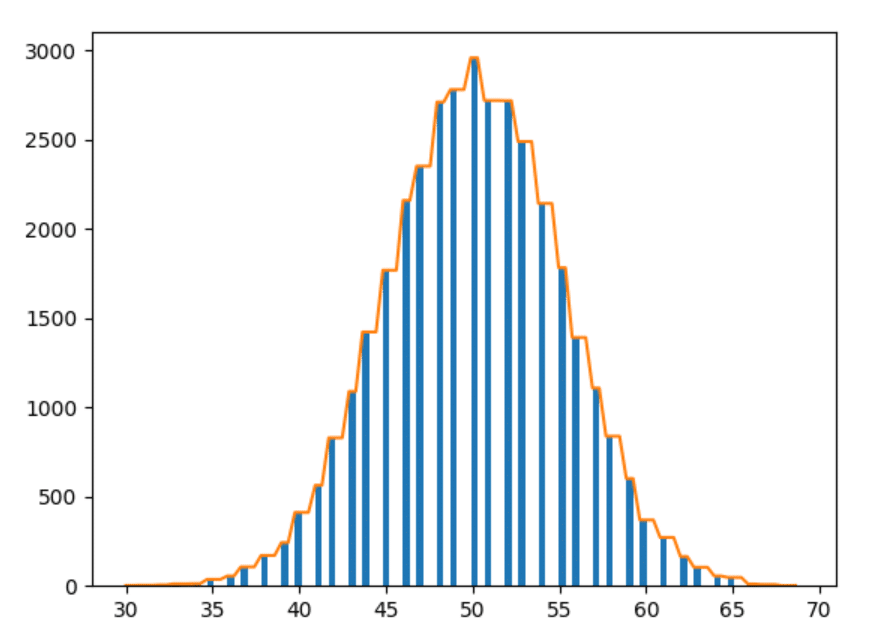
D'accord - le dernier. Traçons les données de 1000 ans.

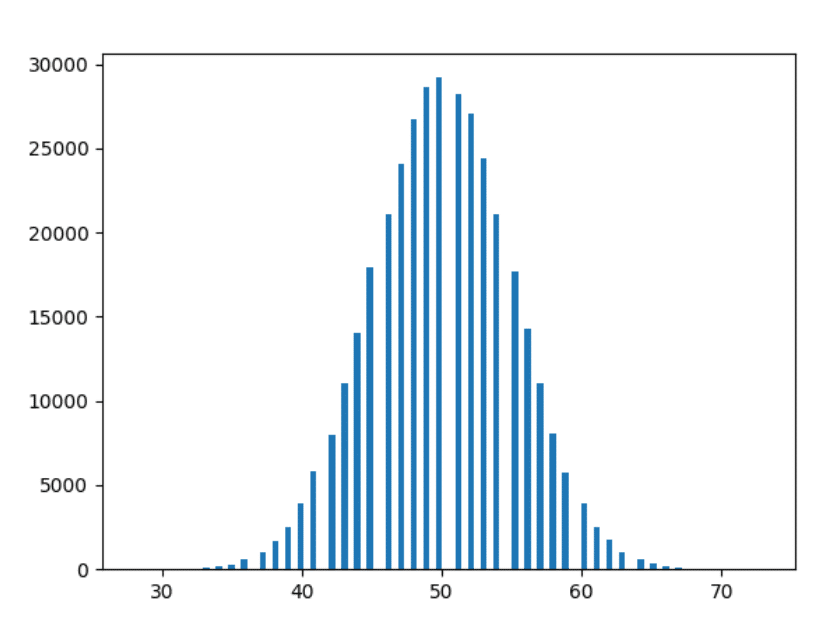
Observations

1. Plus nous expérimentons, plus les formes sont lisses.
2. Plus nous expérimentons, plus les barres suivent les observations ci-dessus (c'est-à-dire que les barres à une distance similaire prennent des formes plus proches).

Où est la foutue distribution normale

D'accord - trop de fond - maintenant, venons-en au fait.

Voyons la réponse suggérée par Google :

Quelques éléments dans cette définition :

Variable aléatoire : En termes simples, une variable aléatoire est un ensemble de valeurs possibles d'une expérience aléatoire comme un tirage au sort. Dans notre exemple, la valeur possible de notre expérience est Head ou Tail .

En forme de cloche : avez- vous remarqué que notre histogramme prend la forme d'une cloche ?

Symétrique : les barres à la même distance ont des formes similaires - n'est-ce pas symétrique ?

Ainsi, la distribution normale représente la distribution des résultats pour des événements comme le tirage au sort - où la distribution a tendance à conserver quelques propriétés, notamment la symétrie et la forme en cloche.

Quels phénomènes autres que le tirage au sort suivent une distribution normale ?

Quelques exemples sympas ici.

• Taille dans la population - plus de personnes entrent dans le groupe de taille moyenne. Il est rare de trouver des personnes extrêmement grandes ou extrêmement petites. Et les chances de trouver extrêmement grand et extrêmement petit sont presque égales.
• Lancer un dé
• Pointure
• QI
• Et bien d'autres…

Ces phénomènes suivent-ils strictement la distribution normale ?

La réponse simple est non. Bien que, comme nous l'avons vu ci-dessus, plus vous expérimentez, plus les données suivront les propriétés de distribution normales. Mais rien ne garantit qu'un événement improbable ne se produira pas de toute façon.

Toutes les distributions de probabilité dans l'univers sont-elles des distributions normales ?

Non. De nombreux phénomènes sont déterminés par un autre type de distribution.

• La probabilité qu'un nombre donné de clients arrivent, d'appels téléphoniques, d'accidents, d'événements sportifs et d'inondations suit la loi de Poisson .
• Pour les ventes aux entreprises, 20 % des clients d'une entreprise sont responsables de 80 % des ventes. ( Distribution de Pareto )
• Schémas de circulation dans une ville — Distribution exponentielle
• Sélection aléatoire des membres d'une équipe parmi une population de filles et de garçons — Distribution hypergéométrique

Et beaucoup plus …

J'ai produit la liste ci-dessus en recherchant simplement sur Google "exemple de la vie réelle" avec certaines distributions répertoriées ici - pas que je les comprenne toutes. 😉

Y a-t-il une raison pour laquelle certains phénomènes naturels ont tendance à suivre une distribution normale

Oui - citant mon explication préférée :

L'explication habituelle est donnée par un autre nom pour la distribution normale, qui est la "distribution d'erreurs". L'idée est que les erreurs sont généralement aléatoires, de sorte qu'elles sont aussi susceptibles d'aller dans un sens que dans l'autre. Par exemple, le tireur est aussi susceptible de tirer un peu vers la gauche, qu'un peu vers la droite, ou un peu haut qu'un peu bas. Ainsi, un graphique de la distance entre les tirs et la cible reflétera cette tendance aléatoire et sera symétrique autour de la moyenne. De même, pour la taille et l'intelligence, de nombreux gènes (peut-être des milliers) contribuent à ces résultats, tout comme un grand nombre de facteurs environnementaux, tels que la nutrition, les maladies, les faibles revenus, etc.

Paramètres de distribution normale

Si vous avez une intuition de la discussion jusqu'à présent, vous êtes déjà le gagnant. Mission accomplie. Le reste de l'article est un bonus.

Tous les graphiques de distribution normale que vous voyez sont de forme différente. Certains d'entre eux sont plus plats que d'autres. Certains d'entre eux ont de bonnes hauteurs. Toutes ces formes sont contrôlées par seulement 2 paramètres :

Moyenne

La moyenne est définie par la moyenne. Il définit la hauteur de la cloche. Pour l'exemple du tirage au sort, la moyenne est proche de 50, qui est l'emplacement le plus élevé du graphique.

Écart-type

Puisque je promets que cet article sera exempt d'équations, je ne donne pas ici sa représentation mathématique. Mais ce n'est quand même pas si difficile. L'écart type est une mesure qui représente la diversité des données.

Par exemple, l'écart type d'âge dans la garde d'enfants sera inférieur à l'écart type d'âge dans le fan club de football, car l'écart d'âge entre le groupe le plus jeune et le groupe le plus âgé devrait être beaucoup plus élevé dans le fan club de football.

L'écart type détermine la largeur de la courbe. Un petit écart type produit une courbe raide et un écart type plus grand produit une courbe plus plate.