Ressentez le calcul avec votre sens de la programmation

Je crois que les gens qui peuvent coder — ont la capacité de comprendre des concepts plus compliqués que le calcul. L'une des raisons pour lesquelles il existe de nombreux programmeurs talentueux qui ont encore du mal avec le calcul n'est pas que c'est difficile. C'est principalement parce qu'on nous l'a enseigné de la mauvaise manière (ainsi que de nombreux autres sujets).

Si vous avez fait du codage dans votre vie - même des exercices ludiques comme la génération de nombres premiers, vous avez peut-être déjà fait des choses similaires qui se produisent en calcul mais n'avez jamais eu la chance de comprendre.

L'objectif de cet article n'est ni de vous apprendre le calcul ni la programmation, mais de vous aider à relier certains points.

J'arriverai à la partie codage dans une minute. Mais permettez-moi de vous donner un bref aperçu avant cela.

Taux de changement

Le calcul différentiel parle de "taux de changement". Essayons de comprendre ce que cela signifie.

Pour un changement d'une variable (x), le taux de changement d'une fonction est simplement le changement de la fonction divisé par le changement de x. Visualisons avec des nombres réels :

Considérons 2 points x=2 et x=6, et une fonction y=f(x) = x².

Considérez également dx = distance entre ces 2 points sur l'axe des x. Et dy est la distance entre les valeurs y pour ces valeurs x.

Ensuite, le taux de variation de y de x=2 à x=6 est

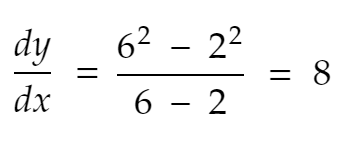
Dérivé

Or — la dérivée dy/dx est le taux de variation de y pour une variation infinitésimale de x. Puisque cette distance (6–2=4) n'est pas infiniment petite - même pas proche, nous ne pouvons pas appeler l'équation ci-dessus une dérivée. Alors, choisissons un nombre plus petit, 0,1, pour l'instant.

Lorsque x = 0, y = x² = 0² = 0.

Voisin le plus proche de la direction positive, x = 0,1. Là, y devient 0,1² = 0,01.

Alors,

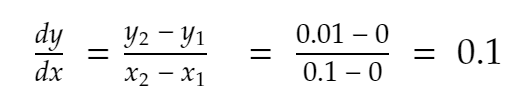
Essayons encore une fois. Plus proche voisin de 0,1 de la direction positive, x = 0,2. Ainsi, y devient 0,2² = 0,04. Alors,

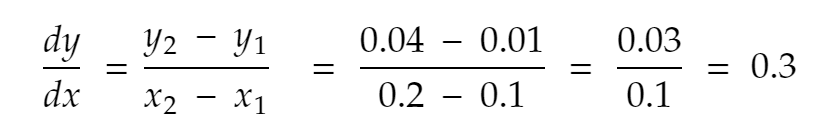
Si nous répétons le processus plusieurs fois, voici ce que nous obtenons :

Voici le fichier excel si vous souhaitez jouer avec.

dx (qui est notre distance infiniment petite fictive entre 2 points adjacents sur l'axe des x) est de 0,1 dans notre contexte.

x augmente en conséquence.

y est simplement x².

dy est la distance entre 2 valeurs y adjacentes. Par exemple, lorsque x = 0,1, la distance entre le y actuel (0,01 ) et le y suivant (0,04) est de 0,03 - donc, dy est de 0,03 à x = 0,1.

dy/dx est dy divisé par dx.

dy/dx / x est dy/dx divisé par x.

Notez maintenant que, à mesure que x augmente, la dernière ligne se rapproche de 2, ce qui signifie — le taux de variation de x² par rapport à x se rapproche du double de x, soit 2x .

Rappelez-vous la dérivée de x² par rapport à x ? 2x ! Trouver une connexion?

Temps de codage

Essayons les choses dans le code dont nous avons discuté jusqu'à présent.

En supposant que vous avez déjà installé Python, dans le terminal, exécutez :

Après cela, exécutez le code Python suivant :

Ici:

x : contenant des nombres de 0 à 9.

y : un autre tableau, chaque élément est le carré de l'élément x correspondant

dy : Un autre tableau initialisé avec des zéros. Nous mettrons les distances y dans ce tableau.

dydx : Un autre tableau initialisé avec des zéros. Il contiendra la valeur dy/dx de chaque point.

dx : Assez évident — c'est la taille du pas. Distance entre 2 nombres consécutifs, qui diminue à mesure que SIZE augmente. Si TAILLE = 10, dx = 1. Si TAILLE = 100, dx = 0,1.

Tout d'abord, nous dérivons dy pour chaque point. Ensuite, nous calculons dydx à partir de celui-ci.

Remarquerez que:

Ici, nous omettons les première et dernière valeurs. La première valeur de x est 0, ce qui produira une erreur de division par zéro. Et nous ne pouvons pas calculer la dernière valeur de dy/dx puisque nous n'avons pas la dernière valeur de dy — car cela nécessiterait à côté de la dernière valeur disponible de y, que nous n'avons pas ici.

Si tout se passe bien, vous obtiendrez ce graphique :

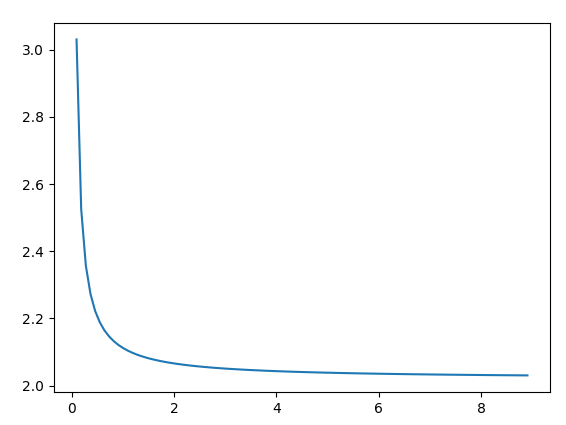
Ce que vous comprenez de l'intrigue

Comme vous le voyez, le graphique se rapproche de 2. Augmentez la valeur de SIZE (ce qui signifie un réglage inférieur de dx) et voyez comment le graphique se rapproche plus rapidement de 2.

Dérivée seconde

Maintenant que vous êtes arrivé jusqu'ici, quelques étapes de plus pour réaliser la dérivée seconde, qui vous donnera l'intuition des dérivées de n'importe quel ordre.

Comme vous vous en souvenez, la dérivée seconde est le taux de variation de la dérivée première par rapport à x. En termes simples, dy/dx dans la dérivée seconde est comme y dans la dérivée première.

Apportons les modifications suivantes au code ci-dessus :

Déclarez 2 autres tableaux :

d2ydx2 : Qui représentera la dérivée seconde :

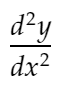
distance_dydx : pour représenter la distance entre la valeur dy/dx entre 2 points adjacents

Voici le code complet de la dérivée seconde :

Après avoir calculé dydx dans la boucle for, nous exécutons une autre boucle pour calculer la dérivée seconde. Avec un codage judicieux, nous pourrions calculer la dérivée seconde dans la même boucle (essayez comme exercice) - mais je les ai gardés séparés ici pour plus de clarté.

Notez également que :

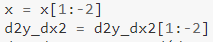
Comme nous l'avons fait dans la dérivée première, nous omettons également certaines valeurs ici. Les 2 dernières valeurs sont omises car la seconde à partir de la dernière nécessiterait la dernière valeur de "première dérivée", que nous ne pourrions pas calculer (puisque nous n'avions pas la valeur y requise pour cela - comme décrit ci-dessus). Cela signifie-t-il que nous devons omettre les 3 dernières valeurs dans le cas de la dérivée 3 ? 🤔 - c'est à vous de trouver.

Voici le graphique de sortie :

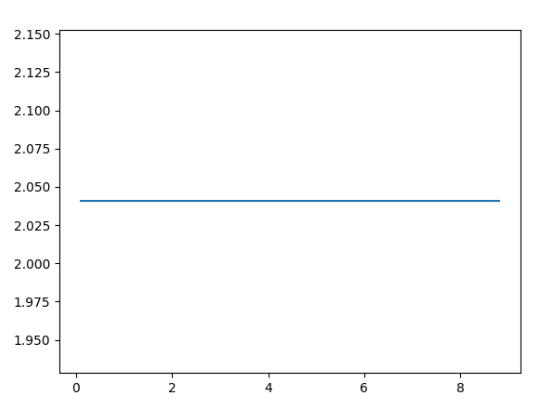
Que voyons-nous ici ?

Comme tu le sais depuis le lycée :

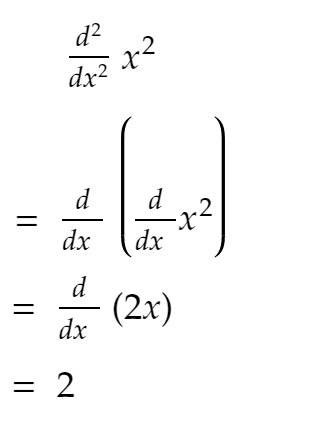
Maintenant, comme vous le voyez dans le code ci-dessus, la dérivée seconde reste la plupart du temps constante, et si vous continuez à augmenter SIZE, elle approche 2 !

Pourquoi le taux de changement est important

Vous vous demandez peut-être :

— Pourquoi traversons-nous tous ces vilains ennuis ? Quelles informations utiles obtenons-nous du taux de variation ou de la dérivée ?

— Pourquoi ne pouvons-nous pas nous contenter du taux de change pour n'importe quel montant ? Pourquoi seulement infiniment petit ? Quelles informations obtenons-nous du taux de variation par rapport à infiniment petit , qui ne peuvent pas être trouvées à partir du taux de variation par rapport aux valeurs plus grandes ?

— Cette chose infiniment petite ressemble un peu à un hack ? Nous avons travaillé avec quelques petits nombres au-dessus, mais sûrement pas infiniment petits.

Si je me permettais de continuer, vous repartiriez en voyant la longueur de cet article et vous ne seriez pas allé aussi loin. Peut-être aborderons-nous ces questions un autre jour 😀.