Statistiques bayésiennes : l'introduction rapide et sans hype d'un testeur A/B
Publié: 2022-06-23
Êtes-vous confiant dans votre capacité à interpréter les résultats fournis par votre outil de test A/B ?
Supposons que vous utilisiez un outil basé sur des statistiques bayésiennes et qu'il vous indique que « B » a 70 % de chances de battre « A », donc « B » est le gagnant. Savez-vous ce que cela signifie et comment cela devrait éclairer votre stratégie CRO ?
Dans cet article, vous apprendrez les bases des statistiques bayésiennes qui vous aideront à reprendre le contrôle de vos tests A/B, y compris
- Une vision impartiale des statistiques bayésiennes
- Avantages et inconvénients fréquentistes vs bayésiens
- La préparation dont vous avez besoin pour interpréter et utiliser en toute confiance les résultats des tests A/B bayésiens tout en évitant certains mythes courants.
- Qu'est-ce que la statistique bayésienne ?
- L'histoire de l'origine bayésienne
- Un exemple de statistiques bayésiennes appliquées aux tests A/B
- Petit glossaire des termes bayésiens importants pour les testeurs A/B
- Inférence bayésienne
- Probabilite conditionnelle
- Distribution de probabilité/distribution de vraisemblance
- Répartition des croyances antérieures
- Conjugaison
- Prieurs conjugués
- Fonction de perte
- Qu'est-ce que la statistique fréquentiste ?
- Test A/B bayésien vs fréquentiste
- Le cadre fréquentiste
- Le cadre bayésien
- Que vous disent réellement les statistiques bayésiennes dans les tests A/B ?
- Probabilité d'être le meilleur (P2BB)
- Hausse attendue
- Perte attendue
- Mythes autour des statistiques bayésiennes à éviter
- Mythe #1 : Les bayésiens énoncent leurs hypothèses, les fréquentistes ne le font pas
- Mythe #2. Les méthodes bayésiennes vous donnent les réponses que vous voulez réellement
- Mythe #3 : L'inférence bayésienne vous aide à mieux communiquer l'incertitude que l'inférence fréquentiste
- Mythe #4. Les résultats des tests A/B bayésiens sont insensibles aux regards indiscrets
- Mythe #5. Les statistiques fréquentistes sont inefficaces puisque vous devez attendre une taille d'échantillon fixe
- Alors, devriez-vous choisir bayésien ou fréquentiste ? Il y a une place pour les deux.
- Clé à emporter
Prêt? Commençons par les bases.
Qu'est-ce que la statistique bayésienne ?
Les statistiques bayésiennes sont une approche de l'analyse statistique basée sur le théorème de Bayes, qui met à jour les croyances sur les événements à mesure que de nouvelles données ou preuves sur ces événements sont collectées. Ici, la probabilité est une mesure de la croyance qu'un événement se produit.
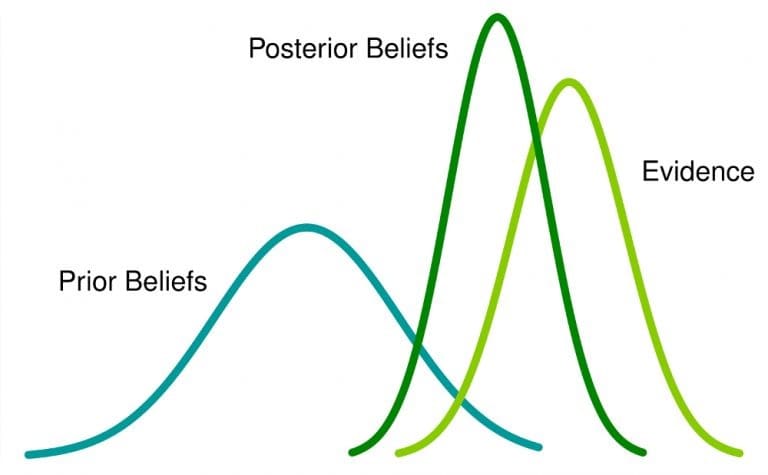
Ce que cela signifie : si vous avez une croyance antérieure à propos d'un événement et que vous obtenez plus d'informations à ce sujet, cette croyance changera (ou du moins sera ajustée) en une croyance postérieure .
Ceci est utile pour comprendre l'incertitude ou lorsque vous travaillez avec de nombreuses données bruyantes, comme dans l'optimisation du taux de conversion pour le commerce électronique et l'apprentissage automatique.
Imaginons ceci :
Supposons, par exemple, que vous regardiez une course de chariots d'épicerie à l'université, puis qu'un spectateur excité vous défie de parier que le mec en t-shirt rouge qui transporte la dame en chemise verte gagnera. Vous y réfléchissez et répliquez que le gars à la veste noire et la fille à capuche noire gagneront à la place.

Un autre spectateur vous a chuchoté un pourboire : "Le gars au t-shirt rouge a remporté les 3 dernières courses sur 4." Que devient votre pari ? Vous n'êtes plus trop sûr, n'est-ce pas ?
Supposons que vous appreniez également que la dernière fois que le gars de la veste noire a porté ses lunettes de soleil porte-bonheur, il a gagné. Et les fois où il ne l'a pas porté, le gars au t-shirt rouge a gagné.
Aujourd'hui, vous voyez que le gars de la veste noire porte ces lunettes. Votre croyance change à nouveau. Vous avez maintenant plus confiance en votre pari, n'est-ce pas ? Dans cette histoire, vous avez mis à jour votre conviction chaque fois que vous avez obtenu la preuve de nouvelles données. C'est l'approche bayésienne.
L'histoire de l'origine bayésienne
Lorsque le révérend Thomas Bayes a pensé pour la première fois à sa théorie, il ne pensait pas qu'elle valait la peine d'être publiée. Ainsi, il est resté dans ses notes pendant plus d'une décennie. C'est lorsque sa famille a demandé à Richard Price de parcourir ses notes que Price a découvert les notes qui constituaient le fondement du théorème de Bayes.
Cela a commencé par une expérience de pensée pour Bayes. Il a pensé à s'asseoir dos à une table parfaitement plate et carrée et à demander à un assistant de lancer une balle sur la table.
La balle pouvait atterrir n'importe où sur la table, mais Bayes pensait pouvoir deviner où en mettant à jour ses suppositions avec de nouvelles informations. Lorsque la balle atterrissait sur la table, il demandait à l'assistant de lui dire si elle atterrissait à gauche ou à droite, devant ou derrière l'endroit où la balle précédente avait atterri.
Il nota cela et écouta alors que d'autres balles atterrissaient sur la table. Avec des informations supplémentaires comme celle-ci, il a découvert qu'il pouvait améliorer la précision de ses suppositions à chaque lancer. Cela a amené l'idée de mettre à jour notre compréhension à mesure que nous acquérions plus de preuves à partir de l'observation.
L'approche bayésienne de l'analyse des données est appliquée dans divers domaines tels que la science et l'ingénierie, et inclut même le sport et le droit.
Dans les expériences contrôlées randomisées en ligne, en particulier les tests A/B, vous pouvez utiliser l'approche bayésienne en 4 étapes :
- Identifiez votre distribution antérieure.
- Choisissez un modèle statistique qui reflète vos convictions.
- Exécutez l'expérience.
- Après observation, mettez à jour vos croyances et calculez une distribution a posteriori.
Vous mettez à jour vos croyances en utilisant un ensemble de règles appelé l'algorithme bayésien.
Un exemple de statistiques bayésiennes appliquées aux tests A/B
Illustrons un exemple de test A/B bayésien.
Imaginez que nous effectuions un simple test A/B sur le bouton CTA d'une boutique Shopify. Pour "A", nous utilisons "Ajouter au panier" et pour "B", nous utilisons "Ajouter à votre panier".
Voici comment un fréquentiste abordera le test.
Il existe deux mondes alternatifs : un où A et B ne sont pas différents, de sorte que le test ne montrera aucune différence de taux de conversion. C'est l'hypothèse nulle. Et dans l'autre monde, il y a une différence, donc un bouton fonctionnera mieux que l'autre.
Le fréquentiste supposera que nous vivons dans le monde 1 où il n'y a pas de différence dans les boutons CTA, c'est-à-dire en supposant que l'hypothèse nulle est vraie. Et ensuite, ils essaieront de prouver que c'est faux à un niveau de certitude prédéterminé appelé le niveau de signification.
Mais voici comment un bayésien abordera le même test :
Ils partent du principe que les boutons A et B ont des chances égales de produire un taux de conversion compris entre 0 et 100 %. Donc, il y a l'égalité des boutons dès le départ - les deux ont 50% de chances d'être les plus performants.
Ensuite, le test commence et les données sont collectées. En observant de nouvelles informations, les testeurs A/B bayésiens mettront à jour leurs connaissances. Donc, si B est prometteur, ils peuvent atteindre une croyance a posteriori basée sur cette observation en disant : « B a 61 % de chances de battre A ».
Il existe des différences fondamentales entre les deux méthodes.
C'est pourquoi il est important pour nous de conserver une approche impartiale des tests A/B bayésiens.
La plupart des outils de test A/B bayésiens - peut-être à des fins de marketing - adoptent une position anti-fréquentiste extrême et poussent l'argument selon lequel le bayésien est meilleur pour vous dire quelle variante est la plus "rentable".
Mais est-ce qu'une seule approche statistique des tests A/B détient les droits exclusifs sur les informations ?
Si l'on pousse l'argument bayésien plus loin, on peut être confronté à des études où les répondants disent qu'ils veulent savoir quelle est la meilleure ligne de conduite ou qu'ils veulent maximiser les profits ou quelque chose de similaire. Cela place fermement la question dans le territoire de la théorie de la décision - quelque chose sur lequel ni l'inférence bayésienne ni l'inférence fréquentiste ne peuvent avoir leur mot à dire.
Georgi Georgiev, créateur de Analytics-toolkit.com et auteur de « Méthodes statistiques dans les tests A/B en ligne »
Nous allons plonger brièvement dans ces détails dans les sections à venir. Pour l'instant, facilitons la compréhension du reste de cette introduction.
Petit glossaire des termes bayésiens importants pour les testeurs A/B
Inférence bayésienne
L'inférence bayésienne met à jour la probabilité d'une hypothèse avec de nouvelles données. Il est construit autour de croyances et de probabilités.
L'inférence bayésienne exploite la probabilité conditionnelle pour nous aider à comprendre l'impact des données sur nos croyances. Disons que nous commençons avec une croyance préalable que le ciel est rouge. Après avoir examiné certaines données, nous nous rendrions vite compte que cette croyance antérieure est fausse. Ainsi, nous effectuons une mise à jour bayésienne pour améliorer notre modèle incorrect sur la couleur du ciel, aboutissant à une croyance a posteriori plus précise .
Michael Berk dans Vers la science des données
Probabilite conditionnelle
La probabilité conditionnelle est la probabilité d'un événement étant donné qu'un autre événement s'est produit. C'est-à-dire la probabilité de A sous la condition B.
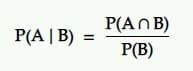
Traduction : La probabilité qu'un événement A se produise compte tenu d'un autre événement B est égale à la probabilité que B et A se produisent ensemble divisée par la probabilité de l'événement B.
Distribution de probabilité/distribution de vraisemblance
Les distributions de probabilité sont des distributions qui montrent la probabilité que vos données prennent une valeur spécifique.
Lorsque vos données peuvent prendre plusieurs valeurs, par exemple, une catégorie comme les couleurs qui pourraient être grises, rouges, orange, bleues, etc., votre distribution est multinomiale. Pour un ensemble de nombres, la distribution peut être normale. Et pour les valeurs de données qui pourraient être oui/non ou vrai/faux, ce serait binomial.
Répartition des croyances antérieures
Ou la distribution de probabilité a priori, simplement appelée a priori, exprime votre croyance avant que vous n'obteniez la preuve de nouvelles données. C'est donc une expression de votre croyance initiale que vous allez mettre à jour après avoir examiné certaines preuves en utilisant l'analyse bayésienne (ou l'inférence).
Conjugaison
Tout d'abord, conjugué fait référence à être réunis, généralement par paires. Dans la théorie bayésienne des probabilités, la conjugaison suppose que l'a priori est conjugué à la vraisemblance.
Si le postérieur a la même forme fonctionnelle que le prior, alors le prior est conjugué à la fonction de vraisemblance. Cela montre comment la fonction de vraisemblance met à jour la distribution a priori.
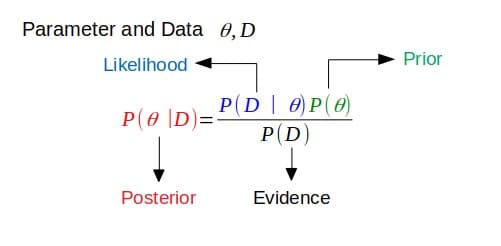
Prieurs conjugués
Ceci est lié à la définition ci-dessus. Si la distribution a posteriori appartient à la même famille de distribution de probabilité (ou a la même forme fonctionnelle) que la distribution de probabilité a priori, alors la distribution a priori et la distribution a posteriori sont des distributions conjuguées. Dans ce cas, l'a priori est appelé a priori conjugué pour la fonction de vraisemblance.
Ils peuvent être subjectifs (basés sur les connaissances de l'expérimentateur), objectifs et informatifs (basés sur des données historiques) ou non informatifs.
Fonction de perte
Une fonction de perte est un moyen de quantifier la perte en mesurant à quel point notre estimation actuelle est mauvaise. Cela nous aide à minimiser les pertes pour les tests d'hypothèses, en particulier lors de l'expression d'une inférence qui se situe dans une plage de valeurs probables, et à prendre des décisions à l'aide des résultats de nos tests.
Maintenant que c'est réglé, nous pouvons passer à autre chose.
Si vous êtes dans le quartier depuis un certain temps, vous avez probablement rencontré plus de quelques mèmes statistiques fréquentistes vs bayésiens.

Les deux parties semblent chercher des réponses dans des directions opposées, mais est-ce vraiment le cas ? Pour mieux comprendre cela (tout en restant impartial), visitons le camp des fréquentistes.
Qu'est-ce que la statistique fréquentiste ?
C'est la première technique inférentielle que la plupart des gens apprennent en statistique. Les statistiques fréquentistes calculent la probabilité qu'un événement (hypothèse) se produise fréquemment dans les mêmes conditions.
Les tests d'hypothèses A/B utilisant l'approche fréquentiste suivent ces étapes :
- Énoncer quelques hypothèses. Typiquement, l'hypothèse nulle est que la nouvelle variante "B" n'est pas meilleure que l'originale "A" tandis que l'hypothèse alternative déclare le contraire.
- Déterminez à l'avance une taille d'échantillon à l'aide d'un calcul de puissance statistique , sauf si vous utilisez des approches de test séquentiel. Utilisez un calculateur de taille d'échantillon qui tient compte de la puissance statistique, du taux de conversion actuel et de l'effet détectable minimum.
- Exécutez le test et attendez que chaque variation soit exposée à la taille d'échantillon prédéterminée.
- Calculez la probabilité d'observer un résultat au moins aussi extrême que les données sous l'hypothèse nulle (valeur de p). Rejetez l'hypothèse nulle et déployez la nouvelle variante en production si la valeur p < 5 %.
Comment cela se compare-t-il au bayésien ? Voyons voir…
Test A/B bayésien vs fréquentiste
C'est un débat notoire partout où l'inférence statistique est utilisée. Et pour être franc, cela ne sert à rien. Les deux ont leurs mérites et des cas où ils sont la meilleure méthode à utiliser.
Contrairement à ce que la plupart des promoteurs des deux camps vous feront penser, ils sont similaires à plusieurs égards et aucun n'est plus proche de la vérité que l'autre - bien que leurs approches diffèrent.
Lorsqu'elle est appliquée aux tests A/B, par exemple, aucune méthode spécifique ne vous donnera une prédiction absolue et précise en termes de plan d'action qui entraînera la croissance de l'entreprise. Au lieu de cela, les tests A/B vous aident à éliminer le risque lié à la prise de décision.
Quelle que soit la façon dont vous analysez vos données - en utilisant des approches bayésiennes ou fréquentistes - vous pouvez agir avec un certain niveau de certitude que vous avez raison.
Et pour cette raison, les deux modèles statistiques sont valides. Le bayésien peut avoir un avantage en termes de vitesse, mais il est plus exigeant en termes de calcul que le fréquentiste.
Découvrez d'autres différences…
Le cadre fréquentiste
La plupart d'entre nous connaissent l'approche fréquentiste des cours d'introduction aux statistiques. Nous avons défini la méthodologie ci-dessus - depuis la déclaration de l'hypothèse nulle, la détermination de la taille de l'échantillon, la collecte de données via une expérience randomisée et enfin l'observation d'un résultat statistiquement significatif.
Dans le fréquentisme, nous considérons la probabilité comme fondamentalement liée à la fréquence des événements répétés. Ainsi, dans un tirage au sort équitable, un fréquentiste pense que s'il devine assez souvent, il obtiendra pile 50 % du temps et il en sera de même pour pile.
État d'esprit fréquentiste : "Si je répète l'expérience dans les mêmes conditions encore et encore, quelles sont les chances que ma méthode obtienne la bonne réponse ?"
Le cadre bayésien
Alors que l'approche fréquentiste traite le paramètre de population pour chaque variante comme une constante (inconnue), l'approche bayésienne modélise chaque valeur de paramètre comme une variable aléatoire avec une certaine distribution de probabilité.
Ici, vous calculez directement les distributions de probabilité (et donc les valeurs attendues) pour les paramètres qui vous intéressent.
Et afin de modéliser la distribution de probabilité pour chaque variante, nous nous appuyons sur la règle de Bayes pour combiner les résultats de l'expérience avec toute connaissance préalable que nous avons sur la métrique d'intérêt. On peut simplifier les calculs en utilisant un a priori conjugué.
Alex Birkett a résumé l'algorithme bayésien de cette façon :
- Définissez la distribution a priori qui intègre vos croyances subjectives sur un paramètre. Le prior peut être non informatif ou informatif.
- Recueillir des données.
- Mettez à jour votre distribution antérieure avec les données à l'aide du théorème de Bayes (bien que vous puissiez avoir des méthodes bayésiennes sans utilisation explicite de la règle de Bayes - voir Bayésien non paramétrique) pour obtenir une distribution postérieure. La distribution postérieure est une distribution de probabilité qui représente vos croyances mises à jour sur le paramètre après avoir vu les données.
- Analysez la distribution a posteriori et résumez-la (moyenne, médiane, sd, quantiles…).
En bref, l'expérimentateur bayésien se concentre sur sa propre perspective et sur ce que la probabilité signifie pour lui. Leur opinion évolue avec les données observées. Les fréquentistes, quant à eux, croient que la bonne réponse se trouve quelque part.

Comprenez que le débat fréquentiste vs bayésien n'a pas beaucoup d'impact sur l'analyse des tests post-A/B. Les différences majeures entre les deux camps sont davantage liées à ce qui peut être testé.
Les statistiques de probabilité ne sont généralement pas utilisées dans une large mesure dans les analyses ultérieures. L'argument bayésien-fréquentiste est plus applicable en ce qui concerne le choix des variables à tester dans le paradigme A/B, mais même là, la plupart des testeurs A/B violent l'enfer des hypothèses de recherche, des probabilités et des intervalles de confiance .
Dr Rob Balon à CXL
Georgi précise :
Il existe plusieurs calculatrices bayésiennes en ligne et au moins un grand fournisseur de logiciels de test A/B appliquant un moteur statistique bayésien qui utilisent tous des priors dits non informatifs (un peu impropre, mais ne creusons pas là-dedans). Dans la plupart des cas, les résultats de ces outils coïncident numériquement avec les résultats d'un test fréquentiste sur les mêmes données. Disons que l'outil bayésien rapportera quelque chose comme '96% de probabilité que B soit meilleur que A' tandis que l'outil fréquentiste produira une valeur p de 0,04 qui correspond à un niveau de confiance de 96%.
Dans une situation comme celle-ci, qui est beaucoup plus courante que certains ne voudraient l'admettre, les deux méthodes conduiront à la même inférence et le niveau d'incertitude sera le même, même si l'interprétation est différente.
Que dirait un bayésien de ce résultat ? Transforme-t-il la valeur p en une probabilité a posteriori appropriée lors de la visualisation d'un scénario dans lequel il n'y a pas d'information préalable ? Ou toutes ces applications de tests bayésiens sont-elles erronées pour l'utilisation d'un a priori non informatif en soi ?
Il n'est vraiment pas nécessaire de choisir un camp et de trouver un endroit à l'abri pour jeter des pierres sur l'autre camp. Il y a même des preuves que les deux cadres produisent les mêmes résultats. Peu importe la route que vous choisissez, la destination sera probablement la même. Cela dépend de la façon dont vous pouvez y arriver avec Frequentist vs Bayesian.
Par exemple:
- Certaines données montrent que les tests bayésiens sont plus rapides et constituent le choix préféré pour les expériences interactives :
Étant donné que le paradigme bayésien permet aux expérimentateurs de quantifier formellement la croyance et d'incorporer des connaissances supplémentaires, il est plus rapide que l'analyse statistique traditionnelle.
Dans une simulation de test A/B bayésien, lorsque le critère de décision a été ajusté (c'est-à-dire en augmentant la tolérance aux erreurs), 75 % des expériences ont conclu à moins de 22,7 % des observations requises par l'approche traditionnelle (à un niveau de signification de 5 %). Et il n'a enregistré que 10% d'erreur de type II. - Le bayésien est également considéré comme plus indulgent, tandis que le fréquentiste a une aversion pour le risque :
Alors que de nombreux tests fréquentistes utilisent une signification statistique de 95 %, les bayésiens peuvent se contenter de moins que cela. Si une variante a 78% de chances de battre le contrôle, en fonction de la perte attendue, cela pourrait être une bonne décision de déployer cette variante.
Si vous vous trompez et que la perte attendue est inférieure à un pour cent, c'est un dommage assez insignifiant pour de nombreuses entreprises. Cette approche décousue peut être mieux adaptée à une prise de décision rapide dans des scénarios à très faible risque. - Cependant, les simulations et les calculs bayésiens sont lourds en calcul :
Frequentist, en revanche, est basé sur le stylo et le papier. Mise en garde : si votre outil de test A/B utilise Bayesian et que vous ne savez pas quelles hypothèses sont ajoutées à vos données, vous ne pouvez pas vous fier à la « réponse » que votre fournisseur vous donne. Prenez-le avec une pincée de sel. Et exécutez votre propre analyse.
Ce n'est pas tout le soleil et les arcs-en-ciel avec Bayesian. Comme le souligne Georgi avec cette liste de questions :
- "Voulez-vous obtenir le produit de la probabilité a priori et de la fonction de vraisemblance ?"
- "Voulez-vous le mélange de probabilités a priori et de données en sortie ?"
- "Voulez-vous que des croyances subjectives soient mélangées aux données pour produire le résultat ?" (si vous utilisez des priors informatifs)
- "Seriez-vous à l'aise de présenter des statistiques dans lesquelles des informations préalables supposées être hautement certaines se mélangent aux données réelles ?"
Ce sont tous des aspects des statistiques bayésiennes, en termes simples.
Que vous disent réellement les statistiques bayésiennes dans les tests A/B ?
Vous avez conçu votre test A/B pour donner un aperçu de la façon dont un changement affecte votre métrique d'intérêt, comme le taux de conversion ou le revenu par visiteur.
Lorsque vous utilisez un outil qui fonctionne avec des statistiques bayésiennes, il est important de comprendre ce que vos résultats signifient car « B est le gagnant » ne signifie pas exactement ce que la plupart des gens pensent qu'il signifie.
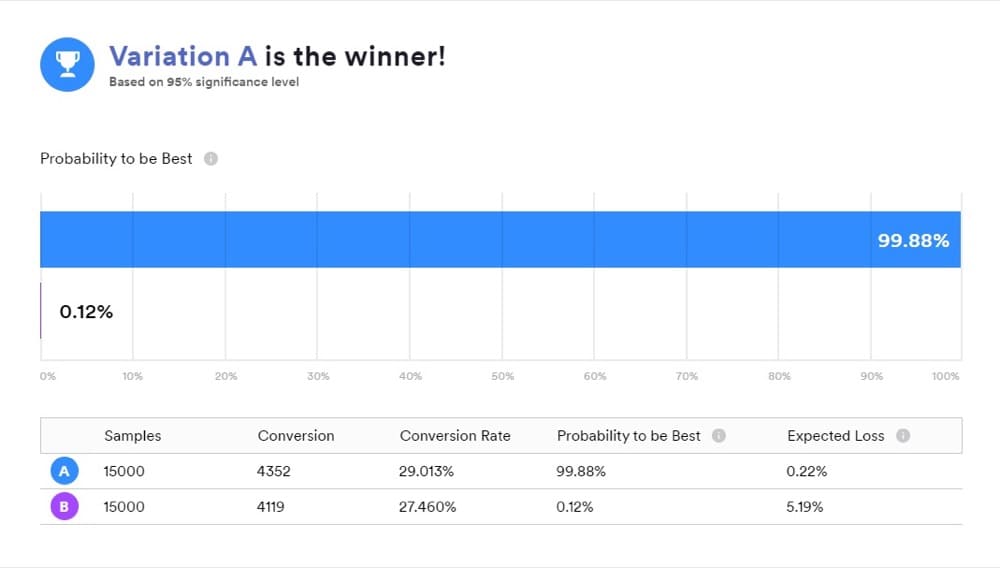
C'est un moyen pratique de présenter les résultats, mais ce n'est pas ce que votre test a révélé. Au lieu de cela, les réponses que vous voulez sont dans des comparaisons postérieures de « A » et « B ».
Voici les 3 méthodes de comparaison :
Probabilité d'être le meilleur (P2BB)
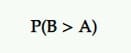
Il s'agit de la probabilité qui déclare un gagnant dans les tests A/B bayésiens.
La variante avec la probabilité d'être la meilleure est celle qui a la plus forte probabilité de continuer à surpasser l'autre.
Ceci est calculé à partir d'un ensemble d'échantillons postérieurs de la mesure d'intérêt de l'original et du challenger.
Ainsi, si B a la plus forte probabilité d'augmenter vos taux de conversion, par exemple, B est déclaré gagnant.
Hausse attendue
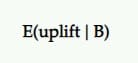
Donc, si B est le gagnant, quelle amélioration devrions-nous en attendre ? Continuerait-il à fournir les mêmes résultats que ceux que nous avons vus lors du test ?
C'est l'idée que l'uplift attendu cherche à fournir. L'amélioration attendue du choix de B plutôt que A, étant donné un ensemble d'échantillons postérieurs, est définie comme l'intervalle crédible (ou moyenne) de l'augmentation en pourcentage.
Dans les tests A/B, nous comparons généralement cela en tant que challenger par rapport au contrôle. Ainsi, si le challenger a perdu, il est représenté en valeurs négatives (comme -11,35%) et en valeurs positives (comme +9,58%) s'il a gagné.
Perte attendue
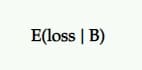
Puisqu'il n'y a pas une probabilité de 100 % que B soit meilleur que A, il y a une chance d'enregistrer une perte si vous choisissez B plutôt que A. Ceci est représenté comme une perte attendue et, tout comme avec une augmentation attendue, il est exprimé à partir du point de vue du challenger contre le contrôle.
Il vous indique le risque de choisir votre variante P2BB (c'est-à-dire le gagnant déclaré).
Avant de plonger dans les mythes, un grand merci à la légende de l'analyse Georgi Georgiev. Ses analyses approfondies de l'inférence fréquentiste vs bayésienne et de la probabilité et des statistiques bayésiennes dans les tests A/B ont inspiré la section suivante.
Mythes autour des statistiques bayésiennes à éviter
Avec une rivalité presque aussi ancienne qu'inutile, le débat bayésien contre fréquentiste a recueilli de nombreuses contributions - et a donné lieu à de nombreux mythes.
Le plus grand de ces mythes (mythe #2) est promu par les fournisseurs d'outils de test A/B pour vous dire pourquoi une approche est meilleure que l'autre.
Mais après avoir lu les sections ci-dessus, vous savez mieux.
Révélons les trous dans ces mythes.
Mythe #1 : Les bayésiens énoncent leurs hypothèses, les fréquentistes ne le font pas
Cela suggère que les bayésiens font des hypothèses sous la forme de distributions a priori et que celles-ci sont ouvertes à l'évaluation. Mais les fréquentistes font des hypothèses qui sont cachées au milieu des mathématiques.
Pourquoi c'est faux : les bayésiens et les fréquentistes font des hypothèses sous-jacentes similaires, la seule différence est que les bayésiens font des hypothèses supplémentaires - en plus des calculs.
Les modèles fréquentistes utilisent des hypothèses mathématiques, telles que la forme de la distribution, l'homogénéité ou l'hétérogénéité de l'effet entre les observations et l'indépendance de l'observation. Et ils ne sont pas cachés. En fait, ils sont largement discutés dans la communauté statistique et énoncés pour chaque test statistique fréquentiste.
La vérité : les fréquentistes énoncent explicitement leurs hypothèses et vont plus loin pour tester les hypothèses : tests de normalité, test d'adéquation de l'ajustement (sous lequel nous avons le test d'inadéquation du rapport d'échantillonnage), et plus encore.
Mythe #2. Les méthodes bayésiennes vous donnent les réponses que vous voulez réellement
L'idée fausse ici est que les valeurs de p et les intervalles de confiance ne disent pas aux testeurs ce qu'ils veulent savoir, contrairement aux probabilités postérieures et aux intervalles crédibles. Les gens veulent savoir des choses comme
- La probabilité que B surpasse A et
- La probabilité que le résultat ne soit pas une coïncidence.
Les valeurs P et les tests d'hypothèse (inférence directe) ne fournissent pas cette information, mais l'inférence inverse le fait.
Pourquoi c'est faux : C'est une question de linguistique. En règle générale, lorsque les non-statisticiens utilisent des termes comme « vraisemblance », « chance » et « probabilité », ils ne les utilisent pas avec leur signification technique à l'esprit. Sondez plus profondément et vous constaterez qu'ils sont tout aussi confus à propos de l'inférence inverse qu'à propos de l'inférence directe.
Selon Georgi Georgiev, des questions comme celles-ci commencent à surgir :
- « Qu'est -ce qu'une probabilité a priori ? Quelle valeur cela apporte-t-il ?
- « Qu'est-ce qu'une fonction de vraisemblance ? »
- "Quelle probabilité 'antérieure', je n'ai pas de données préalables ?"
- « Comment défendre le choix d'une probabilité a priori ? »
- "Existe-t-il un moyen de communiquer exactement ce que disent les données, sans aucun de ces mélanges ?"
La vérité : il devrait y avoir une meilleure compréhension de ce que les testeurs veulent savoir, et non de leur mauvaise interprétation des termes techniques. Les valeurs P, les intervalles de confiance et autres vous indiquent dans quelle mesure les résultats sont bien vérifiés avec les données recueillies. Ils ont fourni une mesure de certitude sans l'influence d'hypothèses antérieures subjectives et non testées.
Mythe #3 : L'inférence bayésienne vous aide à mieux communiquer l'incertitude que l'inférence fréquentiste
Parce que les résultats des tests produisent des informations plus « significatives ».
Pourquoi c'est faux : Les approches fréquentistes et bayésiennes ont des outils similaires pour vous aider à communiquer la certitude et les résultats de votre test A/B.
| fréquentiste | Bayésien | ||||||||||
| ● Estimations ponctuelles | ● Estimations ponctuelles | ||||||||||
| ● Valeurs P | ● Intervalles crédibles | ||||||||||
| ● Intervalles de confiance | ● Facteurs de Bayes | ||||||||||
| ● Courbes de valeur P | ● Distributions postérieures (accomplir la même tâche comme les courbes fréquentistes) | ||||||||||
| ● Courbes de confiance | |||||||||||
| ● Courbes de sévérité, etc. |
La vérité : Tout dépend de la façon dont vous les utilisez. Les deux méthodes sont tout aussi efficaces pour communiquer l'incertitude. Cependant, il existe des différences dans la façon dont ils présentent la mesure de l'incertitude.
Mythe #4. Les résultats des tests A/B bayésiens sont insensibles aux regards indiscrets
Certains statisticiens bayésiens affirment que « vous pouvez arrêter un test bayésien une fois que vous voyez un « gagnant clair » et que cela fait peu de différence pour le résultat final.
Vous savez probablement que cela est inacceptable dans les tests fréquentistes, c'est donc considéré comme un inconvénient par rapport au bayésien. Mais est-ce vraiment ?
Pourquoi c'est faux : Dans une étude de 1969 dans le Journal of the Royal Statistical Society intitulée « Tests répétés de signification sur l'accumulation de données », Armitage et al. ont montré comment l'arrêt facultatif basé sur les résultats augmente la probabilité d'erreur.
Vous ne pouvez pas simplement vous arrêter lorsque vous remarquez un gagnant, mettre à jour votre postérieur et l'utiliser comme votre prochain prior sans ajuster le fonctionnement de l'analyse bayésienne.
La vérité : Peeking affecte l'inférence bayésienne autant que fréquentiste (si vous voulez le faire correctement).
Mythe #5. Les statistiques fréquentistes sont inefficaces puisque vous devez attendre une taille d'échantillon fixe
Certains membres de la communauté CRO pensent que les tests statistiques fréquentistes doivent être exécutés avec une taille d'échantillon fixe et prédéterminée, sinon les résultats ne sont pas valides.
En conséquence, vous attendez plus longtemps que nécessaire pour obtenir les résultats souhaités.
Pourquoi c'est faux : les statistiques fréquentistes n'ont plus été utilisées de cette façon depuis environ sept décennies maintenant. Avec les tests séquentiels fréquentistes, vous n'avez pas besoin d'une durée fixe prédéterminée.
La vérité : Les tests séquentiels, qui sont plus populaires aujourd'hui, nécessitent une taille d'échantillon maximale pour équilibrer les erreurs de type I et de type II, mais la taille réelle de l'échantillon utilisée varie d'un cas à l'autre en fonction du résultat observé.
Alors, devriez-vous choisir bayésien ou fréquentiste ? Il y a une place pour les deux.
Il n'est pas nécessaire de choisir un camp. Les deux méthodes ont leur place. Par exemple, un projet à long terme qui utilise des a priori mis à jour et qui nécessite des résultats rapides se comporte mieux avec l'approche bayésienne.
La méthode fréquentiste, en revanche, est la mieux adaptée aux projets qui nécessitent une quantité importante de répétabilité dans leurs résultats. Comme dans l'écriture de logiciels que de nombreuses personnes avec de nombreux ensembles de données utiliseront.
Comme le dit Cassie Kozyrkov, responsable de l'intelligence décisionnelle chez Google, "les statistiques sont la science qui permet de changer d'avis dans l'incertitude".
Dans sa vidéo récapitulative Bayesian vs Frequentist Statistics, elle a déclaré :
« Vous pouvez prendre ce débat fréquentiste et bayésien et le résumer à ce sur quoi vous changez d'avis. Les fréquentistes changent d'avis sur les actions, ils ont une action par défaut préférée - peut-être qu'ils n'ont aucune croyance - mais ils ont une action qu'ils aiment dans l'ignorance et ensuite ils demandent : "Est-ce que mes preuves [ou mes données] changent d'avis sur ce geste ? » "Est-ce que je me sens ridicule de le faire sur la base de mes preuves?"
Les bayésiens, en revanche, changent d'avis d'une manière différente. Ils commencent par une opinion, une opinion personnelle exprimée mathématiquement, appelée a priori, puis ils demandent : « Quelle est l'opinion sensée que je devrais avoir après avoir incorporé des preuves ? » Et ainsi les fréquentistes changent d'avis sur les actions, les bayésiens changent d'avis sur les croyances.
Et selon la façon dont vous voulez cadrer votre prise de décision, vous préférerez peut-être choisir un camp plutôt qu'un autre.
En fin de compte, nous nous dirigeons tous vers des conclusions similaires - la différence réside dans la façon dont ces conclusions vous sont présentées.
Si l'inférence fréquentiste et bayésienne étaient des fonctions de programmation, les entrées étant des problèmes statistiques, alors les deux seraient différents dans ce qu'ils renvoient à l'utilisateur. La fonction d'inférence fréquentiste renverrait un nombre, représentant une estimation (généralement une statistique récapitulative comme la moyenne de l'échantillon, etc.), tandis que la fonction bayésienne renverrait des probabilités.
Extrait du livre "Probabilistic Programming & Bayesian Methods for Hackers"
Ce qui n'est pas tout à fait juste, c'est l'affirmation selon laquelle l'un donne des résultats plus pratiques que l'autre.
Clé à emporter
Les statistiques bayésiennes dans les tests A/B consistent en 4 étapes distinctes :
- Identifiez votre distribution antérieure
- Choisissez un modèle statistique qui reflète vos convictions
- Exécutez l'expérience
- Utilisez les résultats pour mettre à jour vos croyances et calculer une distribution a posteriori
Vos résultats vous orienteront vers des probabilités perspicaces. Ainsi, vous saurez quelle variante a la plus grande probabilité d'être la meilleure, votre perte attendue et votre augmentation attendue.
Ceux-ci sont généralement interprétés pour vous par la plupart des outils de test A/B utilisant des statistiques bayésiennes. Mais un expérimentateur approfondi effectuera une analyse post-test pour mieux comprendre ces résultats.
Parce que vous êtes arrivé jusqu'ici, voici un fait amusant pour vous : vous connaissez le portrait de Thomas Bayes que tout le monde connaît ? Celui-ci:

Personne n'est sûr à 100% que c'est lui.